Influence of the stress state on void nucleation and subsequent growth around inclusion in ductile material

Abstract

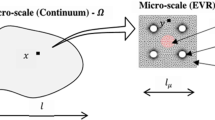
A three-dimensional unit cell model with an inclusion is established, where an interfacial layer between the matrix and inclusion is modeled by a cohesive zone mode. This model is then used to investigate the effect of the stress state of the unit cell on the crack nucleation at the interface and subsequently the void growth, which gives the evolutions of the macro equivalent stress and relative void volume fraction associated with the macro equivalent strain. The interface debonding process indicates that both the stress triaxility and the Lode parameter play a remarkable role in the process and void nucleation and growth. Compared with the model of pure void, the inclusion increases the load carrying capacity and lowers the void growth rate for the same stress triaxiality. Meanwhile the inclusion causes a lag in the expansion of the void due to the interface fracture, which becomes significant as the stress triaxiality increases. The interfacial crack nucleates from different position for different Lode parameter and propagates in different pattern as the Lode parameter changes the principal stresses even for the same stress triaxiality. The two points, where the crack initiates and where the interface is fully debonded, vary with stress triaxiality and Lode parameter, and are getting closer for different Lode parameters when stress triaxiality increases.