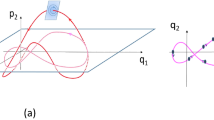
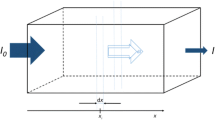
Using Gaussian wave packet solutions, we examine how the kinetic energy is distributed in time-dependent solutions of the Schrödinger equation corresponding to the cases of a free particle, a particle under-going uniform acceleration, a particle in a harmonic oscillator potential, and a system corresponding to all unstable equilibrium. We find, for specific choices of initial parameters, that as much as 90° of the kinetic energy can be localized (at least conceptually) in the ‘front half’ of such Gaussian wave packets, and we visualize these effects.
Similar content being viewed by others
References
1. E. Schrödinger, “Der stetige Übergang von der Mikro- zur Makromechanik,” Naturwiss. 14, 664–666 (1926); translated and reprinted as “The continuous transition from micro- to macro mechanics,” in Collected Papers on Wave Mechanics (Chelsea, New York, 1982), pp 41–44.
2. E. H. Kennard, “The quantum mechanics of an electron or other particle,” J. Franklin Institute 207, 47–78 (1929); see also “Zur quantenmechanik cinfacher Bewegungstypen,” Z. Phys. 44, 326–352 (1927).
3. C. G. Darwin, “Free motion in the wave mechanics,” Proc. Roy. Soc (London) A117, 258–293 (1928).
4. L. de Broglie, Einfuhrung in die Wellenmechanik (Akademie, Leipzig, 1929).
5. E. C. Kemble, The Fundamental Principles of Quantum Mechanics with Elementary Applications (McGraw-Hill, New York, 1937), pp. 35–41.
6. S. Dushman, The Elements of Quantum Mechanics (Wiley, New York, 1938), pp. 405–407.
7. V. Rojansky, Introductory Quantum Mechanics (Prentice Hall, New York, 1938), pp. 69–70.
8. J. R. Hiller, I. D. Johnston, and D. F. Styer, Quantum Mechanics Simulations: The Consortium for Upper-Level Physics Software (Wiley, New York, 1995).
9. B. Thaller, Visual Quantum Mechanics: Selected Topics with Computer-Generated Animations of Quantum-Mechanical Phenomena (Springer, New York, 2000).
10. M. Belloni and W. Christian, “Physlets for quantum mechanics,” Comp. Sci. Eng. 5, 90–97 (2003).
11. R. P. Feynman, “Space-time approach to non-relativistic quantum mechanics,” Rev. Mod. Phys. 20, 367–387 (1948).
12. R. P. Feynman and A. R. Hibbs, Quantum Mechanics and Path Integrals (McGraw-Hill, New York, 1965).
13. D. S. Saxon, Elementary Quantum Mechanics (McGraw-Hill, New York, 1968), pp. 144–147.
14. P. Nardone, “Heisenberg picture in quantum mechanics and linear evolutionary systems,” Am. J. Phys. 61, 232–237 (1993).
15. S. M. Cohen, “Path integral for the quantum harmonic oscillator using elementary methods,” Am. J. Phys. 66, 537–540 (1998).
16. B. R. Holstein, “The harmonic oscillator propagator,” Am. J. Phys. 66, 583–589 (1998).
17. K. Gottfried, Quantum Mechanics: Volume I Fundamentals (Benjamin, New York, 1966), pp. 260–264.
18. D. F. Styer, “The motion of wave packets through their expectation values and uncertainties,” Am. J. Phys. 58, 742–744 (1990).
19. A. S. de Castro and N. C. da Cruz, “A pulsating Gaussian wave packet,” Eur. J. Phys. 20, L19–L20 (1999).
20. W. Waldenström and Razi K. Naqvi, “A neglected aspect of the pulsating Gaussian wave packet,” Eur. J. Phys. 20, L41–L43 (1999).
21. L. I. Schiffer, Quantum Mechanics (1st edn.) (McGraw Hill, New York, 1949), pp. 67–69.
22. D. Bohm, Quantum Theory (Prentice-Hall, Englewood Cliffs, 1951), pp. 306–309.
23. P. Fong, Elementary Quantum Mechanics (Addison-Wesley, Reading, 1962), pp. 88–91.
24. A. Messiah, Quantum Mechanics: Volume I (North-Holland, Amsterdam, 1961), pp. 446–447.
25. D. ter Haar, Selected Problems in Quantum Mechanics (Academic, New York, 1964), pp. 14, 143–145.
26. C. Cohen-Tannoudji, B. Diu, and F. Laloê, Quantum Mechanics, Volume I (Wiley, New York, 1977), pp. 572–573.
27. S. Howard and S. K. Roy, “Minimum uncertainty states and their time evolution,” Am. J. Phys. 53, 538–542 (1985).
28. R. W. Robinett, Quantum Mechanics: Classical Results, Modern Systems, and Visualized Examples (Oxford University Press, New York, 1997), pp. 208–209, 213–214.
29. M. H. Bramhall and B. M. Casper, “Reflections on a wave packet approach to quantum mechanical barrier penetration,” Am. J. Phys. 38, 1136–1145 (1970).
30. M. A. Doncheski and R. W. Robinett, “Anatomy of a ‘quantum bounce’,” Eur. J. Phys. 20, 29-37 (1999).
31. L. de la Torre and F. Gori, “The bouncing bob: quasi-classical states,” Eur. J. Phys. 24, 253–259 (2003).
32. E. Wigner, “On the quantum correction for thermodynamic equilibrium,” Phys. Rev. 40, 749-759 (1932).
33. V. I. Tatarskii, “The Wigner representation of quantum mechanics,” Sov. Phys. Usp. 26 311-327 (1983).
34. N. L. Balaczs and B. K. Jennings, “Wigner’s function and other distribution functions in mock phase space,” Phys. Rep. 105, 347–391 (1984).
35. P. Carruthers and F. Zachariasen, “Quantum collision theory with phase-space distributions,” Rev. Mod. Phys. 55, 245–285 (1983).
36. M. Hillery, R. F. O’Connell, M. O. Scully, and E. P. Wigner, “Distribution functions in physics: Fundamentals,” Phys. Rep. 106, 121–167 (1984).
37. J. Bertrand and P. Bertrand, “A tomographic approach to Wigner’s function,” Found. Phys. 17, 397–405 (1987).
38. Y. S. Kim and E. P. Wigner, “Canonical transformations in quantum mechanics,” Am. J. Phys. 58, 439–448 (1990).
39. Y. S. Kim and M. E. Noz, Phase Space Picture of Quantum Mechanics: Group Theoretical Approach (Lecture Notes in Physics Series, Vol. 40) (World Scientific, Singapore, 1990).
40. H.-W. Lee, “Theory and application of the quantum phase-space distribution functions,” Phys. Rep. 259, 147–211 (1995).
41. A. M. Ozorio de Almeida, “The Weyl representation in classical and quantum mechanics,” Phys. Rep. 296, 265–342 (1998).
42. M. Belloni, M. Doncheski, and R. W. Robinett, “Wigner quasiprobability distribution for the infinite square well: energy eigenstates and time-dependent wave packets,” to appear in Am. J. Phys.; e-print arXiv: quant-ph/0312086.
43. R. W. Robinett and L. C. Bassett, “Analytic results for Gaussian wave packets in four model systems: II. Autocorrelation functions,” to appear in Found. Phys. Lett.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Robinett, R., Bassett, L. Analytic Results for Gaussian Wave Packets in Four Model Systems: I. Visualization of the Kinetic Energy. Found Phys Lett 17, 607–625 (2004). https://doi.org/10.1007/s10702-004-1117-9
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10702-004-1117-9