Skip to main content
SpringerLink
Log in

A decomposition heuristic to solve the two-stage lot sizing and scheduling problem with temporal cleaning

  • Published:
Flexible Services and Manufacturing Journal Aims and scope Submit manuscript

Abstract

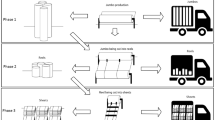
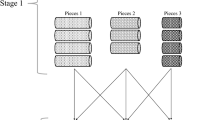
This paper presents a study on the fruit-based beverage lot sizing and scheduling problem. This is a two-stage lot-scheduling problem with some features, such as the presence of buffers between the production stages, mandatory temporal cleanings for the preparation tanks (stage I) and production lines (stage II), and production synchronization between the production stages. To solve this problem, we propose two variations of a two-phase heuristic algorithm by devising a production stage decomposition scheme coupled with a constructive procedure. In the first phase, a one-stage lot sizing is solved by a mixed integer programming model, and in the second phase, scheduling and the synchrony between the stages are carried out using a constructive algorithm. The two variations of the heuristic are: Stage I Heuristics (S1H) and Stage II Heuristics (S2H). In S1H, production stage I is solved by a mathematical model and in S2H, production stage II is solved by another mathematical model. Data from a typical beverage company of a large worldwide brand was used in the computational tests. The results showed that the heuristics are able to find competitive solutions very quickly and that the S2H heuristic performs better than S1H.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  • Almeder C, Almada-Lobo B (2011) Synchronisation of scarce resources for a parallel machine lotsizing problem. Int J Prod Res 49:7315–7335

    Article  Google Scholar 

  • Almeder C, Klabjan D, Traxler R, Almada-Lobo B (2015) Lead time considerations for the multi-level capacitated lot-sizing problem. Eur J Oper Res 241(3):727–738

    Article  MathSciNet  MATH  Google Scholar 

  • Araujo SA, Arenales MN, Clark AR (2008) Lot-sizing and furnace scheduling in small foundries. Comput Oper Res 35:916–932

    Article  MATH  Google Scholar 

  • Baldo TA, Santos MO, Almada-Lobo B, Morabito R (2014) An optimization approach for the lot sizing and scheduling problem in the brewery industry. Comput Ind Eng 72:58–71

    Article  Google Scholar 

  • Bitran G, Yanasse H (1992) Computational complexity of the capacitated lot size problem. Manag Sci 28:1174–1186

    Article  MathSciNet  MATH  Google Scholar 

  • Bouchriha H, Ouhimmou M, D’Amours S (2007) Lot sizing problem on a paper machine under a cyclic production approach. Int J Prod Econ 105(2):318–328

    Article  Google Scholar 

  • Brahimi N, Dauzere-Peres S, Najid NM, Nordli A (2006) Single item lot sizing problems. Eur J Oper Res 168:1–16

    Article  MathSciNet  MATH  Google Scholar 

  • Camargo VC, Mattiolli L, Toledo FM (2012) A knapsack problem as a tool to solve the production planning problem in small foundries. Comput Oper Res 39:86–92

    Article  MathSciNet  MATH  Google Scholar 

  • Camargo VC, Toledo FM, Almada-Lobo B (2012) Three time-based scale formulations for the two-stage lot sizing and scheduling in process industries. J Oper Res Soc 63:1613–1630

    Article  Google Scholar 

  • Camargo VC, Toledo FM, Almada-Lobo B (2014) Hops—hamming-oriented partition search for production planning in the spinning industry. Eur J Oper Res 234(1):266–277

    Article  MathSciNet  MATH  Google Scholar 

  • Christou I, Lagodimos A, Lycopoulou D (2007) Hierarchical production planning for multi-product lines in the beverage industry. Prod Plan Control 18(5):367–376

    Article  Google Scholar 

  • Clark AR, Morabito R, Toso EA (2010) Production setup-sequencing and lot-sizing at an animal nutrition plant through ATSP subtour elimination and patching alistair. J Sched 13(2):111–121. https://doi.org/10.1007/s10951-009-0135-7

    Article  MATH  Google Scholar 

  • Copil K, Wörbelauer M, Meyr H, Tempelmeier H (2016) Simultaneous lotsizing and scheduling problems: a classification and review of models. OR Spectr. https://doi.org/10.1007/s00291-015-0429-4

    Article  MATH  Google Scholar 

  • Díaz-Madroñero M, Mula J, Peidro D (2014) A review of discrete-time optimization models for tactical production planning. Int J Prod Res 52(17):5171–5205

    Article  MATH  Google Scholar 

  • Dolan E, Moré J (2002) Benchmarking optimization software with performance profiles. Math Program 91:201–213

    Article  MathSciNet  MATH  Google Scholar 

  • Drexl A, Haase K (1995) Proportional lotsizing and scheduling. Int J Prod Econ 40:73–87

    Article  Google Scholar 

  • Drexl A, Kimms A (1997) Lot sizing and scheduling—survey and extensions. Eur J Oper Res 99:221–235

    Article  MATH  Google Scholar 

  • Euromonitor (2015) Market research on fruit and vegetable juice. Technical reports, Euromonitor International

  • Ferreira D, Morabito R, Rangel S (2009) Solution approaches for the soft drink integrated production lot sizing and scheduling problem. Eur J Oper Res 196:697–706

    Article  MATH  Google Scholar 

  • Ferreira D, Morabito R, Rangel S (2010) Relax and fix heuristics to solve one-stage one-machine lot-scheduling models for small-scale soft drink plants. Comput Oper Res 37(4):684–691

    Article  MATH  Google Scholar 

  • Ferreira D, Clark AR, Almada-Lobo B, Morabito R (2012) Single-stage formulations for synchronised two-stage lot sizing and scheduling in soft drink production. Int J Prod Econ 136(2):255–265

    Article  Google Scholar 

  • Fleischmann B (1990) The discrete lot sizing and scheduling problem. Manag Sci 44:337–348

    MathSciNet  MATH  Google Scholar 

  • Fleischmann B, Meyr H (1997) The general lotsizing and scheduling problem. OR Spectr 19:11–21

    Article  MathSciNet  MATH  Google Scholar 

  • Furlan M, Almada-Lobo B, Santos M, Morabito R (2015) Unequal individual genetic algorithm with intelligent diversification for the lot-scheduling problem in integrated mills using multiple-paper machines. Comput Oper Res 59:33–50

    Article  MathSciNet  MATH  Google Scholar 

  • Glock CH, Grosse EH, Ries JM (2013) The lot sizing problem: a tertiary study. Int J Prod Econ 155:39–51

    Article  Google Scholar 

  • Guimarães L, Klabjan D, Almada-Lobo B (2012) Annual production budget in the beverage industry. Eng Appl Artif Intell 25(2):229–241

    Article  Google Scholar 

  • Gunther H (2008) The block planning approach: a case study application from the beverage industry. In: 2008 IEEE international conference on industrial engineering and engineering management, pp 359–363

  • Hans E, Van De Velde S (2011) The lot sizing and scheduling of sand casting operations. Int J Prod Econ 49(9):2481–2499

    Article  Google Scholar 

  • Jans R, Degraeve Z (2008) Modeling industrial lot sizing problems: a review. Int J Prod Econ 46(6):1619–1643

    Article  MATH  Google Scholar 

  • Karimi B, Ghomi SF, Wilson J (2003) The capacitated lot sizing problem: a review of models and algorithms. Omega 31:365–378

    Article  Google Scholar 

  • Karimi-Nasab M, Modarres M (2015) Lot sizing and job shop scheduling with compressible process times: a cut and branch approach. Comput Ind Eng 85:196–205

    Article  Google Scholar 

  • Kopanos GM, Puigjaner L, Georgiadis MC (2011) Resource-constrained production planning in semicontinuous food industries. Comput Chem Eng 35(12):2929–2944

    Article  Google Scholar 

  • Kopanos GM, Puigjaner L, Maravelias CT (2011) Production planning and scheduling of parallel continuous processes with product families. Ind Eng Chem Res 50(3):1369–1378

    Article  Google Scholar 

  • Luche JRD, Morabito R, Pureza V (2009) Combining process selection and lot sizing models for production scheduling of electrofused grans. Asia-Pac J Oper Res 26(03):421–443

    Article  MATH  Google Scholar 

  • Marinelli F, Nenni ME, Sforza A (2007) Capacitated lot sizing and scheduling with parallel machines and shared buffers: a case study in a packaging company. Ann Oper Res 150(1):177–192

    Article  MathSciNet  MATH  Google Scholar 

  • Mateus GR, Ravetti MG, Souza MC, Valeriano TM (2010) Capacitated lot sizing and sequence dependent setup scheduling: an iterative approach for integration. J Sched 13(3):245–259

    Article  MathSciNet  MATH  Google Scholar 

  • Menezes GC, Mateus GR, Ravetti MG (2016) A hierarchical approach to solve a production planning and scheduling problem in bulk cargo terminal. Comput Ind Eng 97:1–14

    Article  Google Scholar 

  • Meyr H (2002) Simultaneous lotsizing and scheduling on parallel machines. Eur J Oper Res 139(2):277–292

    Article  MathSciNet  MATH  Google Scholar 

  • Meyr H, Mann M (2013) A decomposition approach for the general lotsizing and scheduling problem for parallel production lines. Eur J Oper Res 229(3):718–731

    Article  MATH  Google Scholar 

  • Pacheco J, Ángel Bello F, Álvarez A (2013) A multi-start tabu search method for a single-machine scheduling problem with periodic maintenance and sequence-dependent set-up times. J Sched 16(6):661–673

    Article  MathSciNet  Google Scholar 

  • Pagliarussi M, Morabito R, Santos M (2017) Optimizing the production scheduling of fruit juice beverages using mixed integer programming models. Gestão Produção 24(1):64–77

    Article  Google Scholar 

  • Ramezanian R, Fallah Sanami S, Shafiei Nikabadi M (2017) A simultaneous planning of production and scheduling operations in flexible flow shops: case study of tile industry. Int J Adv Manuf Technol 88:2389–2403

    Article  Google Scholar 

  • Santos MO, Almada-Lobo B (2012) Integrated pulp and paper mill planning and scheduling. Comput Ind Eng 63:1–12

    Article  Google Scholar 

  • Sel C, Bilgen B (2014) Hybrid simulation and mip based heuristic algorithm for the production and distribution planning in the soft drink industry. J Manuf Syst 33(3):385–399

    Article  Google Scholar 

  • Shamsaei F, Vyve MV (2017) Solving integrated production and condition-based maintenance planning problems by mip modeling. Flex Serv Manuf J 29(2):184–202

    Article  Google Scholar 

  • Silva C, Magalhaes JM (2006) Heuristic lot size scheduling on unrelated parallel machines with applications in the textile industry. Comput Ind Eng 50:76–89

    Article  Google Scholar 

  • Tempelmeier H, Copil K (2015) Capacitated lot sizing with parallel machines, sequence-dependent setups, and a common setup operator. OR Spectr 38(4):819–847

    Article  MathSciNet  MATH  Google Scholar 

  • Toledo CFM, Kimms A, França PM, Morabito R (2015) The synchronized and integrated two-level lot sizing and scheduling problem: evaluating the generalized mathematical model. Math Probl Eng 2015:1–18

    Article  MathSciNet  MATH  Google Scholar 

  • Toledo CFM, Arantes MdS, Hossomi MYB, Almada-lobo B (2016) Mathematical programming-based approaches for multi-facility glass container production planning. Comput Oper Res 74:92–107

    Article  MathSciNet  MATH  Google Scholar 

  • Transchel S, Minner S, Kallrath J, Lohndorf N, Eberhard U (2011) A hybrid general lot-sizing and scheduling formulation for a production process with a two-stage product structure. Int J Prod Res 49(9):2463–2480

    Article  Google Scholar 

  • Trigeiro WW, Thomas LJ, McClain JO (1989) Capacited lot sizing with setup times. Manag Sci 35:353–366

    Article  Google Scholar 

  • Xiao J, Yang H, Zhang C, Zheng L, Gupta JN (2015) A hybrid lagrangian-simulated annealing-based heuristic for the parallel-machine capacitated lot-sizing and scheduling problem with sequence-dependent setup times. Comput Oper Res 63:72–82

    Article  MathSciNet  MATH  Google Scholar 

  • Yu X, Zhang Y, Steiner G (2014) Single-machine scheduling with periodic maintenance to minimize makespan revisited. J Sched 17:263–270

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors would like to thank the reviewers 1, 2, 3 and 4 for their helpful comments and suggestions, the fruit-based beverage company for its collaboration with this research and FAPESP (Grant 2010/10133-0) and CNPq (Grant No. 312569/2013-0) for their financial support.

Author information

Authors and Affiliations

  1. Production Engineering Department, Federal University of Triângulo Mineiro, Uberaba, MG, Brazil

    Alyne Toscano

  2. Department of Physics, Chemistry and Mathematics, Federal University of São Carlos, Sorocaba, SP, Brazil

    Deisemara Ferreira

  3. Production Engineering Department, Federal University of São Carlos, São Carlos, SP, Brazil

    Reinaldo Morabito

Authors
  1. Alyne Toscano
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Deisemara Ferreira
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Reinaldo Morabito
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Reinaldo Morabito.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Toscano, A., Ferreira, D. & Morabito, R. A decomposition heuristic to solve the two-stage lot sizing and scheduling problem with temporal cleaning. Flex Serv Manuf J 31, 142–173 (2019). https://doi.org/10.1007/s10696-017-9303-9

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10696-017-9303-9

Keywords

Search

Navigation