1 Introduction

Facing diverse consumer preferences and demand uncertainty, flexibility has become critical for manufacturing and service firms to maintain a competitive edge. The importance of flexibility can be demonstrated by recent examples in the automobile industry. In 2000, General Motors saw a surprisingly high demand for its new PT Cruiser model, while the demand for the similar model Neon turned out to be unexpectedly low. As a result, there was a shortage of the PT Cruiser while the dedicated plant for the Neon had excess capacity. This lack of flexibility to reallocate the excess demand to the plant with spare capacity reportedly cost GM an estimated $240 million in pretax profit (Biller et al. 2006).

The Ford Motor Company invested $485 million to retool two Canadian plants with flexible systems. As claimed by the Windsor engine plant manager, Chris Bolen, “The initial investment is slightly higher, but long-term crisis are lower in multiples.” (Knight Ridder Tribune Business News, November 6, 2002). The company also had a plan to convert the systems at most of its engine and transmission plants all over the world to flexible ones.

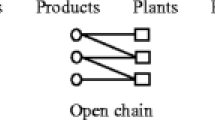
Despite the clear benefits, flexibility requires costly investments. It is often possible to deploy only a limited amount of flexible resources, yet achieve very significant benefits. The idea of “chaining” was proposed by Jordan and Graves (1995) and has become very popular over the past decade. By using 2n links to connect n products and n plants in a chain, it is possible to achieve well above 90% of the benefits of the full network with n 2 links. Jordan and Graves also propose the following guidelines for process flexibility design:

  1. 1.

    Try to equalize the capacity allocated to each product node;

  2. 2.

    Try to equalize the expected demand allocated to each plant node;

  3. 3.

    Construct a long circular chain visiting as many nodes as possible.

These guidelines suggest that chaining works the best when products (and plants) are homogeneous. However, few real systems have these characteristics. When products and plants are nonhomogeneous, it often requires extensive simulation to construct the best possible chaining structure. Besides, the chaining structure does not take into consideration the possibilities that investment and operating costs of different flexible resources can be different. For example, it is cheaper to allow a plant to produce two similar products than to produce very different products.

Resources are seldom perfectly flexible. A resource is almost always better designed for producing one product than others. In other words, there is always efficiency lost when we utilize a resource, even a flexible one, to serve a demand class that it is not primarily designed for. Such inefficiencies may take the form of additional production cost or shrinking capacity. An example of additional production cost is the wages for the extra hours required to train workers and an example cause of shrinking capacity is the changeover time incurred by switching an assembly line to producing a different product. These inefficiencies constitute the “response” dimension of process flexibility (Chou et al. 2008a), which has received far less attention in the literature. In this paper, we will follow the assumption made by Chou et al. and only consider additional production costs.

Ideally, we would like to formulate a combinatorial optimization problem to optimize the network structure. However, this would require solving a two-stage integer stochastic programming problem. In the first stage, we select the subset of links on the network to construct. In the second stage, subject to realized demand, we solve the demand allocation problem which has a network flow structure. The major difficulty of using this approach is that it is difficult to obtain the expected flow of a network under random demand. While it is possible to apply sampling techniques to approximate the recourse function value, this requires a large number of samples since demand is multi-dimensional. The resulting stochastic program would have very large size.

In this paper, we utilize a technique that solves stochastic programming problems with network recourse approximately without sampling. This method is based on Lagrangian relaxation with state-independent multipliers. This method, adopted in studying stochastic programming problems in transportation (e.g., Cheung and Powell 1996) and approximate dynamic programming (e.g., Topaloglu 2009), has proved to be highly efficient. With our solution approach, it is possible to generate high-quality solutions to the network design problem efficiently.

The remainder of this paper is organized as follows. We first review the related literature in Sect. 2. Then in Sect. 3, we formulate the process design model and propose a Lagrangian algorithm to solve it. Section 4 contains computational results that compare the network structures obtained from the optimization approach to the popular chaining structure under different scenarios. Finally, we draw conclusions in Sect. 5.

2 Literature review

The literature on process flexibility can be roughly divided into two streams. In the first stream, the flexibility structure (i.e., the network) is typically assumed to be given. The goal is to optimize the amount of capacity to invest for each of the resources with given flexibility relationships. Harrison and Van Mieghem (1999) formulate this problem as a multidimensional newsvendor problem and show that the optimal capacity levels follow a critical fractile property. This result is generalized by Van Mieghem and Rudi (2002) to the newsvendor networks framework which can model discretionary activities such as transshipment, assembly, commonality and distribution. Chod et al. (2007) study the interactions between operational flexibility and financial hedging and demonstrate conditions under which they work as complements and substitutes in reducing mismatch risk.

The second stream of research mainly focuses on determining the flexibility network structure given the capacity of resources. It is demonstrated in seminal paper by Jordan and Graves (1995) that the chaining structure, in which each product is produced by two plants and each plant produces two products in a “circular” arrangement, achieves almost all of the benefits (measured by expected sales) of a completely flexible network. The impact of their research has been huge, since they show that most of the benefits of full flexibility can be obtained by adding small degrees of flexibility in a clever way.

Since then, the chaining structure has been widely advocated in academia and industry. Graves and Tomlin (2003) extend the results to more general multi-stage supply chains. Aksin and Karaesmen (2006) provide an analytical justification of the chaining structure by showing that the performance of a regular k-chain is increasing and concave in k. A regular k-chain is a symmetric network in which each plant node is connected to k products and each product node is connected to k plant nodes. Their result suggest that the chaining structure (or a 2-chain) provides the largest amount of marginal benefit over an inflexible network (1-chain) and the marginal benefit of adding more links to the network is diminishing.

Recently, Iravani et al. (2005) propose a “structural flexibility matrix” to measure the degree of flexibility of network structures. Chou et al. (2007) use the concept of graph expanders to prove the existence of sparse structures that achieve most of the benefits of the fully flexible system. Chou et al. (2008b) provide further analytical results to compare the chaining structure to the fully flexible system. Using asymptotic analysis, they prove that the chaining structure can achieve about 90% of the benefits of the fully flexible system, even when system size grows very large and demand is uniformly distributed.

All the above studies on flexibility structure focus on the range of the network, i.e., how much of the variable demand the system can capture. Not much effort has been put into the “response” dimension, i.e., how costly it is to cope with varying demand. Chou et al. explicitly study the response dimension by assuming that it costs more for a plant to manufacture products other than those it is primarily designed to produce. This reflects the efficiency loss of utilizing flexible resources, which has been largely ignored in the flexibility structure literature. Their results show that chaining can be less beneficial relative to full flexibility when response is taken into consideration. Nevertheless, they also show that chaining still brings significant benefits over the case with no flexibility.

Another issue that has not received much attention is the cost of investing in flexibility. In the vast majority of work in this stream, the objective is to achieve as much benefits of the fully flexible system with as little added flexibility as possible. The degree of added flexibility is typically measured by the number of arcs added. However in practical situations, adding different links to a network usually require investments of different magnitudes. This is because some related products and their production processes are more similar than we would observe for unrelated products. Therefore ideally, we should attempt to solve a combinatorial network design model that explicitly includes the investment costs of adding arcs and the benefits of operating the constructed network. In this paper, we take a first step in achieving this goal, by formulating a stochastic programming network design model and solving it heuristically using a Lagrangian-based approach.

3 Process flexibility design model

3.1 Model formulation

In this section, we formulate the two-stage stochastic program for process flexibility design. There are n plants (indexed by j) producing n products (indexed by i). Note that we just demonstrate the simple case, where we have an equal number of plants and products, to be consistent with the literature. It will be trivial for us to allow these numbers to be different. The demand for the products, denoted by D, follows a probability distribution F. We assume that F is known in the first stage. The actual realization of D is observed after the first stage decisions are made, but before the beginning of the second stage.

In the first stage, we select a subset of arcs (i, j) to construct, where i, j = 1, 2, … n. If an arc (i, j) is selected, then it is possible to produce product i with plant j in the second stage. Investing in an arc requires a fixed investment f ij , representing the cost of retooling the manufacturing process or purchasing a flexible technology.

At the beginning of the second stage, we first observe the realized demand. With a certain realization D = d, we then optimize the assignment of plant capacities to satisfy product demand. This is done subject to the flexibility structure and capacity levels determined in the first stage. If one unit of plant j’s capacity is assigned to produce product i, a cost of c ij is incurred. Finally, the selling price per unit of product i is p i . The notation is summarized as follows:

Demand and supply parameters

  • i = 1,2 … n: index of products

  • j = 1,2 … n: index of plants

  • D: Demand vector defined over the probability space \((\Upomega, {\mathfrak{F}}, P)\) with elementary outcomes ω ∈ Ω

  • K j : capacity of plant j

Cost parameters

  • f ij : cost to invest in technology that allows plant j to produce product i

  • c ij : cost to produce one unit of product i using plant j

  • p i : marginal revenue from selling one unit of product i

Decision variables

  • Y ij : binary variable which equals 1 if the link (i, j) is constructed, 0 otherwise

  • s ij : number of units of product i to produce using plant j in the second stage

The process design model can then be formulated as follows:

$$ (PD): \max - \sum_{i=1}^n \sum_{j=1}^n f_{ij}Y_{ij} + E\left[ \prod(Y, \omega) \right] $$
(1)

subject to:

$$ Y_{ij} \in \{0,1\},\qquad \hbox{ for}\quad i = 1,2\,\ldots\,n,\,\,j = 1,2\,\ldots\,n $$

The objective (1) is the expected profit for the two-stage problem, including costs of investments in the first stage and the expected operating profit in ths second stage. The profit of the second stage is denoted by the function Π(.). Note that we do not impose constraints requiring that every product be produced by some plant. Therefore in our formulation, a product will not be produced if it is not profitable to do so.

The value of Π(.) is obtained by solving the following second stage (recourse) problem, given a set of first stage decisions (K, Y) and a demand realization D(ω):

$$ \prod(Y, \omega) = \max \sum_{i=1}^n \sum_{j=1}^n (p_i - c_{ij}) s_{ij} $$

subject to:

$$ \begin{array}{ll} \sum\limits_{i=1}^n s_{ij} \leq K_j, & \quad \hbox{ for } j= 1,2,\,\ldots,\,n \\ \sum\limits_{j=1}^n s_{ij} \leq D(\omega), &\quad\hbox{ for } i = 1,2,\,\ldots,\,n \\0 \leq s_{ij} \leq D(\omega) Y_{ij}, &\quad \hbox{ for } i =1,2,\,\ldots,\,n,\,\, j = 1,2,\,\ldots,\,n \end{array}$$

In the second stage problem, we optimize the assignments of capacity to products such that the profit from serving demand is maximized. Note that our formulation is more general than the usual one adopted in the literature that maximizes the flow from plants to products. This is to reflect the more realistic situation where products differ in terms of profitability. The nonhomogeneous assignment costs reflect the efficiency losses incurred when a resource is utilized to produce products for which it is not primarily designed.

In a practical process flexibility setting, we may expect that f jj  = 0 for all j. This suggests that each plant, before any flexibility investments, is primarily dedicated to producing one associated product. It does not require any extra investment to enable a plant to produce its primarily associated products. We may also expect c ii  < c ij for j ≠ i, such that it is more cost efficient to use the primary plant to produce each product rather than to produce it elsewhere.

3.2 Solution approach

We now describe a Lagrangian relaxation algorithm that approximately solves the process design model. To begin, we reformulate the problem (P) by embedding the second stage problem:

$$ (P'): \max - \sum_{i=1}^n \sum_{j=1}^n f_{ij}Y_{ij} + E \left[ \sum_{i=1}^n \sum_{j=1}^n (p_i - c_{ij}) s_{ij}(\omega) \right] $$
(2)

subject to:

$$ \begin{aligned} \sum_{i=1}^n s_{ij}(\omega) &\leq K_j, \quad \hbox{for}\, j = 1,2\,\ldots\,n, \omega \in \Upomega \\ \sum_{j=1}^n s_{ij}(\omega) &\leq D_i(\omega), \quad \hbox{for}\, i = 1,2\,\ldots\,n, \omega \in \Upomega \end{aligned} $$
(3)
$$ \begin{array}{ll} s_{ij}(\omega) \leq D_i(\omega) Y_{ij}, & \quad \hbox{for}\,i = 1,2\,\ldots\,n, j = 1,2\,\ldots\,n, \omega \in \Upomega \\ Y_{ij} \in \{0,1\}, & \quad \hbox{for } i = 1,2\,\ldots\,n, j = 1,2\,\ldots\,n \\ s_{ij}(\omega) \geq 0, & \quad \hbox{for}\,i = 1,2\,\ldots\,n, j = 1,2\,\ldots\,n, \omega \in \Upomega \end{array} $$
(4)

We will relax constraints (4) and (5), imposing Lagrange multipliers τ and η respectively. The Lagrangian dual problem becomes:

$$ \begin{aligned} (LD):\min _{{\tau \ge 0,\eta \ge 0}} \max & - \sum\limits_{{i = 1}}^{n} {\sum\limits_{{j = 1}}^{n} {\left( {f_{{ij}} - \eta _{{ij}} E[D_{i} ]} \right)} } Y_{{ij}} \\ & + E\left[ {\sum\limits_{{i = 1}}^{n} {\sum\limits_{{j = 1}}^{n} ( } p_{i} - c_{{ij}} - \tau _{i} - \eta _{{ij}} )s_{{ij}} (\omega ) + \sum\limits_{{i = 1}}^{n} {\tau _{i} } D(\omega )} \right] \\ \end{aligned} $$

subject to:

$$ \begin{array}{ll} \sum\limits_{i=1}^n s_{ij}(\omega) \leq K_j, & \quad \hbox{for}\,\,j = 1,2\,\ldots\,n, \omega \in \Upomega \\ Y_{ij} \in \{0,1\}, &\quad \hbox{for}\,i = 1,2\,\ldots\,n, j = 1,2\,\ldots\,n \\ s_{ij}(\omega) \geq 0,& \quad \hbox{for}\,i = 1,2\,\ldots\,n,\,\,j = 1,2\,\ldots\,n, \omega \in \Upomega \end{array} $$

Ideally, we would want to use state-dependent dual multiplier values that vary across different states ω ∈ Ω. However, doing so would make the problem intractable as there are potentially an infinite number of states. The use of state-independent dual multipliers in Lagrangian relaxation is a powerful technique to attack loosely-coupled stochastic network flow and stochastic dynamic programming problems (Cheung and Powell 1996, Topaloglu 2009). By using common multiplier values across all states, the upper bounds obtained will be looser than what could (in principle) have been obtained using state-dependent multipliers. The quality of the bounds will be relatively good if the variability across different states is relatively small. For regular random demand fluctuations, these bounds usually perform reasonably well (see, for example, Kunnumkal and Topaloglu 2008 for a discussion).

The inner maximization problem in (LD), given a set of dual multiplier values, is separable by plant j. For each j, we have a subproblem of the form:

$$ (SP_1): \max - \sum\limits_{i=1}^n \left(f_{ij} - \eta_{ij} E[D_i] \right) Y_{ij} + E \left[ \sum\limits_{i=1}^n (p_i - c_{ij} - \tau_i - \eta_{ij}) s_{ij}(\omega) \right] $$
(5)

subject to:

$$ \begin{array}{ll} \sum_{i=1}^n s_{ij}(\omega) \leq K_j, &\quad \hbox{for}\, \omega \in \Upomega \\ Y_{ij} \in \{0,1\}, & \quad \hbox{for}\,i = 1,2\,\ldots\,n \\ s_{ij}(\omega) \geq 0 &\hbox{for } i = 1,2\,\ldots\,n, \omega \in \Upomega \end{array} $$

In (SP 1), the Y ij term can be easily optimized by setting Y ij  = 1 whenever the coefficient is positive and 0 otherwise. The remaining problem in K j and s ij can be viewed as a newsvendor problem with multiple customers and heterogeneous underage costs. To solve this problem, we begin with the following observations. For brevity of notation, we temporarily suppress the subscript j and let \(\hat{p}_{i} = p_{i_1} - c_{i_1} - \tau_{i_1} - \eta_{{i_1}}\).

Observation 1

Suppose there are two products, i 1, i 2, where \( \hat{p}_{i_1} < \hat{p}_{i_2}\). Then if \(s_{i_1}(\omega) >0\) in the optimal solution, \(s_{i_2}(\omega) = D_{i_2}(\omega)\).

Observation 2

If \(\hat{p}_{i} < 0\), s i (ω) = 0 for all ω ∈ Ω.

In words, Observation 1 means that a less profitable product is only produced when all demand for all more profitable products have been satisfied. Observation 2 suggests that a product with negative marginal profit will never be produced. With these observations, we can rank the products such that \(\hat{p}_{1} \geq \hat{p}_{2} \geq \cdots \geq \hat{p}_{m} \geq 0\). The remaining n − m products have negative marginal profit and therefore will not be produced.

Let ρ(k, i) be the probability that the k-th unit of capacity is used to produce product i. Then the objective function (7), excluding the Y terms, is given by:

$$ \begin{aligned} \pi(K) &= \int\limits_0^K \sum_{i=1}^m \hat{p}_i \rho(k,i) \hbox{d}k \\ &= \int\limits_0^K \sum_{i=1}^m \hat{p}_i \left[P\left( \sum_{h=1}^i D_h \geq k \right) - P\left( \sum_{h=1}^{i-1} D_h \geq k \right)\right] \hbox{d}k \\ &= \sum_{i=1}^m \int\limits_0^K (\hat{p}_i- \hat{p}_{i+1}) P\left(\sum_{h=1}^i D_h \geq k \right) \hbox{d}k \end{aligned} $$
(6)

With the above, we can solve the inner maximization problem of (LD) given any set of dual multipliers (τ, η). It is then possible to solve the outer minimization problem using a subgradient procedure. However, the standard procedure (Fisher 1985) cannot be directly applied to compute the step sizes for multiplier update. This is due to the difficulty of computing lower bounds for our problem. Even given the first stage decisions, computing a lower bound for the second stage objective is still difficult, and may require sampling. Sampling-based method may provide probabilistic bounds which are tight only when the number of samples is very large. It is not computationally economical to embed such a subroutine in our algorithm.

Instead, we adopt the the variable target value method (VTVM) proposed by Sherali et al. (2000) to compute step sizes. This procedure guarantees convergence to the global optimal solution of a piecewise linear convex minimization problem without the need for an upper bound.

Note that the lower bound solutions obtained in our algorithm may not be feasible in the original problem, because constraints are relaxed. However, note that any binary values of the first-stage variables (Y) would ensure that a feasible solution to the second-stage exists, i.e., the problem has complete recourse. Moreover, the Y variables are unconstrained, except for the binary requirement. Therefore, the Y values from the lower bound solution produced in each iteration leads us to a feasible solution to the original problem. To estimate the cost of this feasible solution, we need to solve a stochastic linear program, which is equivalent to the original problem with the Y values fixed:

$$ (PF): \max E \left[ \sum_{(i,j):Y_{ij}=1} (p_i - c_{ij}) s_{ij}(\omega) \right] $$

subject to:

$$ \begin{array}{ll} \sum\limits_{i: Y_{ij}=1} s_{ij}(\omega) \leq K_j, & \quad \hbox{for}\,j = 1,2\,\ldots\,n, \omega \in \Upomega \\ \sum\limits_{j: Y_{ij}=1} s_{ij}(\omega) \leq D_i(\omega), & \quad \hbox{for}\,i = 1,2\,\ldots\,n, \omega \in \Upomega \\ Y_{ij} \in \{0,1\}, & \quad \hbox{for}\,i = 1,2\,\ldots\,n,\,\,j = 1,2\,\ldots\,n \\ s_{ij}(\omega) \geq 0, & \quad \hbox{for}\,i = 1,2\,\ldots\,n,\,\,j = 1,2\,\ldots\,n, \omega \in \upomega \end{array} $$
(7)

In this stochastic program to evaluate a feasible solution (PF), we define flow variables (s ij ) only for arcs that are constructed ((i, j) where Y ij  = 1). Note also that we are only interested in estimating the optimal expected profit of this problem, but not the flow variable values. Therefore, our approach is to perform a similar Lagrangian relaxation routine by relaxing constraints (10). Observe that the resulting subproblems are structurally identical to (SP 1) without the Y variables and can be solved using the same procedure. Since the computational effort to estimating the expected profit for a particular network configuration is similar to that of solving the original Lagrangian dual (LD), we only perform this subroutine once in every 20 iterations of the main algorithm.

4 Computational results

4.1 Homogeneous products

In the first computational test, we focus on homogeneous products with the same demand distribution and cost of production. We assume that each plant can produce a specified product without extra investments. To enable a plant to produce a different product besides the specified one, investments must be made to enable the technology. The problem parameters are summarized in Table 1. Note that for this experiment we assume that the marginal cost of any production is 0. Therefore the second stage problem is a maximum flow problem as typically assumed in the literature. Under this second-stage objective and the assumption that all products and plants are homogeneous in demand and cost parameters, we know from the literature that the chaining structure performs extremely well. The goal of this experiment is to show that our algorithm produces solutions that perform similarly well as the those of the chaining heuristic, even under conditions that heavily favor the latter.

Table 1 Input parameters in test of homogeneous products
Full size table

To draw a comparison between our solution and the chaining solution, we vary the investment cost per arc (f ij ) such that our algorithm produces a spectrum of solutions with different numbers of arcs. Then the expected profit is compared to that of the symmetric regular k-chains with k = 1, 2, … n. The second stage profits are displayed in Fig. 1a. Note that in this first graph, we exclude the investment costs to focus on the benefits of adding arcs.

Fig. 1
figure 1

Performance comparison of stochastic programming and chaining solutions on homogeneous problem. a Second-stage profit of SP solution and symmetric k-graph, b overall profit of SP solution and symmetric 2-graph

Full size image

We observe that the two curves are very close to each other, suggesting that the two solution approaches produce solutions of similar quality under homogeneous input parameters. Note that the chaining solution profit slightly outperforms our solution in some instances. This is due to the fact that we cannot solve the network design problem exactly. Nevertheless, it is obvious that our solutions perform about as well as the chaining structure that is well-known to perform the best under the conditions tested in this experiment.

In Fig. 1b, we plot the overall profits (including investment costs) of using stochastic programming and chaining solutions against the investment cost of constructing flexibility links. Note that since chaining always suggests the same network structure, the overall profit decreases linearly with the investment cost requirement. On the other hand, the profit of the stochastic programming solution decreases to a constant when adding links becomes more expensive. This is because adding flexibility links eventually become too expensive and we end up with the solution with dedicated resources. Finally when the investment cost is rather small, the chaining solution can outperform the stochastic programming solution. This is due to the fact that our algorithm to solve the network design problem is not exact.

4.2 Nonhomogeneous demand

We would like to investigate how well our approach works relative to the chaining solution when the products differ in their demand distributions. In the chaining structure, every product i can be produced by plant j = i and plant j = i + 1. When demand distributions are nonhomogeneous, the profit may be sensitive to the sequences of plants and products. For example if there are two high-demand products and two low-demand products, then numbering the high-demand products as i = 1 and 2 will produce a different solution than numbering them as i = 1 and 3 (see Fig. 2). Due to these complications, a direct implementation of the chaining heuristic may be dangerous.

Fig. 2
figure 2

Example of different chaining structures for nonhomogeneous demand case

Full size image

In this experiment, we randomly generate the mean demand for each product from a uniform (0, 400) distribution. The coefficients of variation are set to be equal across all products. We vary this figure from 0.1 to 1 and simulate 100 instances for each value. In Fig. 3, we plot the average overall (two stages combined) profits of the stochastic programming and chaining solutions against the coefficient of variation of demand.

Fig. 3
figure 3

Performance comparison of stochastic programming and chaining solutions with nonhomogeneous demand. a Total profit, b investment cost and second-stage profit

Full size image

We observe from Fig. 3a that with heterogeneous demand distributions, the stochastic programming solution outperforms the chaining solution when demand variability is high or very low. It is intuitive that the optimal degree of flexibility should increase with demand variability. The stochastic programming approach takes this property into account and generates solution with varying levels of flexibility investments to cope with different levels of demand variability (see Fig. 3b). In contrast, the chaining heuristic produces the same network structure under any combination of demand distributions. As a result, the non-adaptive chaining solution performs less well under conditions that favor high degrees (i.e., high demand variability) or low degrees (i.e., low demand variability) of flexibility.

At moderate levels of demand variability, the chaining solution performs slightly better because the stochastic programming problem cannot be solved exactly with our algorithm. This test also demonstrates that the chaining solution performs very well at moderate demand variability levels even when demand distributions of different products are heterogeneous.

4.3 Nonhomogeneous cost

The differences between range and response in process flexibility are highlighted in Chou et al. 2008a. Range refers to the system’s ability to cope with changes of states. Response refers to the ease with which the system adapts to different states. In our paper as well as in theirs, the response dimension is represented by the efficiency loss (i.e., additional cost) incurred when a flexible resource is assigned to producing a product for which it is not primarily designed.

In the first experiment, we set the marginal cost for each plant to produce its primary product (i.e., c ii ) at 0 as in the previous experiments. However, we randomly generate the marginal costs of producing products other than the primary one (i.e., c ij for i ≠ j) from uniform distributions with mean 7.5 (half the selling price of the product). We vary the ranges of the uniform distributions to test the effect of different degrees of product heterogeneity.

In Fig. 4, we plot the average overall profits, investment costs and second-stage profits of the two approaches against the range of the uniform distribution of the marginal production costs. We observe that the stochastic programming solution outperforms the chaining solution (except when the range is very small and the two approaches perform similarly) and the difference increases with the degree of cost heterogeneity. It can be observed that the average profit of the stochastic programming solution increases with the level of cost heterogeneity, while the average profit if the chaining solution stays relatively constant. From Fig. 4b, we also observe that the stochastic programming solution tends to suggest larger investments on flexibility at higher heterogeneity levels. As a result, the second-stage profit of the stochastic programming solution increases.

Fig. 4
figure 4

Performance comparison of stochastic programming and chaining solutions with nonhomogeneous cost parameters. a Total profit, b investment cost and second-stage profit

Full size image

One possible intuitive explanation is that the stochastic programming approach may exploit relationships between products with special network structures when products are asymmetric in terms of cross production (i.e., manufacturing a product with a resource that is not primarily designed for it) costs. When marginal costs of cross production are heterogeneous, the stochastic programming solution chooses low-cost links and avoids high-cost ones. When the degree of heterogeneity is high, there is a high chance that there are a large number of low-cost links that can be taken advantage of. In the extreme case, suppose half of the links have 0 marginal cost and half of them have infinite marginal cost. Then the stochastic programming solution would choose the zero-cost links and avoid the high-cost ones, allowing cross-production at zero cost. This would then generate a higher profit than the symmetric case where all links have equal marginal costs.

On the other hand, the chaining solution does not take into consideration the heterogeneity of products. It turns out that the average performance of chaining is roughly the same under different degrees of cost homogeneity. In a practical situation, the system designer may want to reorder products and plants heuristically and attempt to improve the chaining solution. However, it is difficult to identify the “best” chain using such heuristics. In that case it is better to use the stochastic programming solution.

In the next experiment, we assume that all production costs are 0, but the investment costs for flexibility links (i.e., f ij for i ≠ j) are randomly simulated from uniform distributions with mean 200. We plot the overall profits against the range of the uniform distributions in Fig. 5.

Fig. 5
figure 5

Performance comparison of stochastic programming and chaining solutions with nonhomogeneous investment costs. a Total profit, b investment cost and second-stage profit

Full size image

Similar to the previous case, the performance of the chaining solution is steady under different degrees of heterogeneity of investment costs. On the other hand, the stochastic programming solution generates higher profits when the investment costs are more heterogeneous. From Fig. 5b, we observe that the investment costs of the stochastic programming solution declines with the range of investment costs and the second-stage profit increases slightly. This suggests that the stochastic programming approach is able to select links with low investment costs while maintaining the second-stage performance when the investment costs are more heterogeneous. Thus the stochastic programming approach is more beneficial compared with the chaining solution when costs are more heterogeneous as the former takes advantage of the instance-specific cost structure.

4.4 Optimizing capacity

When designing a network of manufacturing facilities, it is often possible to determine the capacity of plants. Existing models in the literature typically assume given plant capacities and determine the flexibility structure (e.g., Jordan and Graves 1995), or attempt to optimize the capacities given a network structure (e.g., Van Mieghem 1998). In contrast, our stochastic programming model can be adapted to attack the joint problem of capacity investment and flexibility structure design.

Recall the formulation of our network design problem (3). To formulate the joint capacity investment and network design problem, we allow capacities K j to be first-stage decision variables, together with the flexibility investment variables Y ij . We assume a linear investment cost function for capacity with constant marginal investment cost v j per unit. We note that our solution approach outlined below can be easily modified to accommodate general convex investment cost functions. After adding the investment cost term for capacity, the objective function of the stochastic integer program becomes:

$$ (P''): \max - \sum_{j =1}^n v_j K_j - \sum_{i=1}^n \sum_{j=1}^n f_{ij}Y_{ij} + E \left[ \sum_{i=1}^n \sum_{j=1}^n (p_i - c_{ij}) s_{ij}(\omega) \right] $$
(8)

To solve the problem, we follow the same Lagrangian relaxation procedure as discussed previously for the problem with given capacities. The only difference is that K j now becomes a decision variable in subproblem where the objective function becomes:

$$ \begin{aligned} (SP_{2} ):\max - & \sum\limits_{{i = 1}}^{n} {\left( {f_{{ij}} - \eta _{{ij}} E[D_{i} ]} \right)} Y_{{ij}} - v_{j} K_{j} \\ & + E\left[ {\sum\limits_{{i = 1}}^{n} ( p_{i} - c_{{ij}} - \tau _{i} - \eta _{{ij}} )s_{{ij}} (\omega )} \right] \\ \end{aligned} $$
(9)

Again, the optimal Y ij values in (SP 2) can be easily determined by looking at the sign of the coefficients. The objective function excluding the Y terms, as denoted by π(K j ) in (8), is a convex function. Therefore we can easily optimize the capacity K j by taking the first-order condition:

$$ \pi'(K) = \sum_{i=1}^m (\hat{p}_i- \hat{p}_{i+1}) P\left(\sum_{h=1}^i D_h \geq K \right) = v_j $$
(10)

This equation can be solved efficiently using root-finding algorithms (such as Newton’s method). Note that this condition is a generalization of the newsvendor solution. When there is only one product (m = 1), (13) reduces to the well-known newsvendor critical fractile condition.

In short, the joint capacity investment and network design problem can be solved using the same algorithm for the original problem with the modification that the capacity level K j is optimized by solving (13) rather than given as an input parameter.

We test the performance of the two solution approaches under different degrees of heterogeneity of capacity investment costs. We randomly generate the investment cost of the capacity to produce one unit at each plant from random distributions with mean 7.5 (half the selling price of the product). We also generate the mean demands randomly from a uniform (0,400) distribution. The coefficients of variation of demand are set to 0.6, a moderate level.

In Fig. 6, we plot the average performances of the two solution approaches under different degrees of variability of capacity investment costs. From Graph (a), we observe that the chaining solution can outperform the stochastic programming solution when the costs are relatively homogeneous, as happened in the cases discussed previously. However, as the degree of heterogeneity of investment costs across products increases, the stochastic programming solution performs better relatively. At high degrees of heterogeneity, the difference can be very significant.

Fig. 6
figure 6

Performance comparison of stochastic programming and chaining solutions to the joint capacity investment and flexibility design problem. a Total profit, b investment cost and second-stage profit

Full size image

One interesting point to note in Graph (b) is that the stochastic programming solution always builds up capacities in fewer than 20 plants (to produce 20 products). This is beneficial because doing so allows risk-pooling at fewer plants, leading to lower investment costs to satisfy the same amount of demand. Note that it is not necessarily optimal to pool the demands for all products at one plant due to the efficiency loss (i.e., increased production cost) due to cross production. The stochastic programming solution captures the trade-off between the benefits of risk-pooling and the resulting efficiency loss while the chaining solution does not.

As the degree of heterogeneity of investment costs increases, the stochastic programming approach builds up capacity at the low-cost plants and avoids the high-cost ones. As the degree of heterogeneity increases, it becomes more likely that some plants have extremely low investment costs. The stochastic programming approach tends to invest on these few plants and yields higher profits. As fewer plants are used for production, higher investment costs on flexibility are needed. On the other hand, the chaining approach always suggests the same solution using all 20 plants.

5 Conclusions

Process flexibility is critical in manufacturing and service systems with multiple demand classes or products. However, researchers have not attempted to optimize the network structure given nonhomogeneous resource and production costs and demands for products. We take a first step to close this gap by formulating an integer stochastic programming problem and solving it with a Lagrangian relaxation technique.

Our computational results provide some valuable insights. Firstly, we show that even in the case where demand and costs are homogeneous, our algorithm produces solutions that perform almost as well as the chaining solution which is known to perform extremely well under such conditions. Secondly, we show that when mean demands for products are nonhomogeneous, the chaining structure still performs extremely well under moderate values of coefficient of variation of demand. However, when the demand distributions have high or low coefficients of variation, our stochastic programming approach performs better.

Our model also addresses the efficiency loss incurred when utilizing flexibility. Our stochastic programming solution takes advantage of heterogeneity of marginal cross production costs (i.e., efficiency loss) across different plant-product pairs and produces better solutions. Similarly, our solution approach can also take advantage of heterogeneity of investment cost requirements of different flexible resources (or links) and produce solutions with higher profits than in the homogeneous case. Compared to the chaining solution, our approach can be significantly better when cost parameters are heterogeneous.

As a first step towards an optimization approach to the process flexibility problem, our approach provides high quality solutions that outperform those generated by the chaining heuristic in instances with nonhomogeneous cost parameters. However, in homogeneous instances, our approach often performs worse than chaining. This is due to the fact that our algorithm only solves the problem approximately. From this, we note that there is an opportunity to further improve our algorithm and obtain even better solutions for both homogeneous and nonhomogeneous instances. This is one important direction for future research.

In this paper, we have not considered the risk of failures or disruptions of resources. Lim and Daskin (2008) study the differences between disruption of nodes (plants) and links (flexible resources) under the chaining structure. It is an important extension for our model to incorporate the possibility of such disruptions such that the solutions are robust to potential failure of resources.

Another important element that has been ignored in most researches in process flexibility is the dynamics of production over time. In multiple-period problems, it is possible to keep inventory to mitigate mismatch risks, besides utilizing process flexibility (Deng and Shen 2009). Demand evolution over time may also complicate operations. For example, how process flexibility may help in the case where multiple products experience different yet overlapping life cycles is an interesting area for further research.

One related issue is the effect of different demand patterns (e.g., some products may be substitutes or complements of one another). For these situations, Jordan and Graves (1995) provide some qualitative guidelines, such as linking substitutes in the same chain. In reality, however, consumer preferences can be very complicated and thus such simple guidelines may be difficult to implement. For example, product relationships may not be transitive (i.e., A and B are substitutes, B and C are substitutes, but A and C are not). More sophisticated demand modeling will be needed in future research.