ChemiX: a Bragg crystal spectrometer for the Interhelioprobe interplanetary mission

Abstract

Interhelioprobe (IHP), an analogue to the ESA Solar Orbiter, is the prospective Russian space solar observatory intended for in-situ and remote sensing investigations of the Sun and the inner heliosphere from a heliocentric orbit with the perihelion of about 60 solar radii. One of several instruments on board will be the Bragg crystal spectrometer ChemiX which will measure X-ray spectra from solar corona structures. Analysis of the spectra will allow the determination of the elemental composition of plasma in hot coronal sources like flares and active regions. ChemiX is under development at the Wrocław Solar Physics Division of the Polish Academy of Sciences Space Research Centre in collaboration with an international team (see the co-author list). This paper gives an overview of the ChemiX scientific goals and design preparatory to phase B of the instrument development.

Appendices

Appendix A: The geometry of the crystal – detector unit

The ChemiX is an X-ray spectrometer which uses bent crystals as dispersion elements. According to Bragg’s law

$$ 2d \, \sin \, \theta=n\lambda $$

(1)

only X-rays satisfying the Bragg condition, are reflected from the surface of the crystal. Here λ is the incident photon wavelength, d is the spacing of planes in the mono crystal wafer, 𝜃 is the incident angle with respect to the crystal plane, and n is an integer corresponding to the crystal’s reflection order. Therefore, for the bent crystal, in the 1st order reflection wavelength range λ ₁−λ ₂ correspond to the angles 𝜃 ₁−𝜃 ₂ (see Fig. 10).

Fig. 10

Schematic geometry of the crystal-detector section with definition of the angles and other important parameters used

Figure 10 shows the schematic geometry of the crystal-detector unit of the ChemiX spectrometer. The plot is in the rectangular coordinate system with origin at the centre of the crystal curvature. The solar radiation, coming from above, is diffracted by the bent crystal with a radius of curvature r and the surface marked with a thick black solid line. After Bragg reflection it falls on a position-sensitive CCD detector, indicated in the figure with the thick yellow line. ChemiX contains a collimator, which narrows the field of view of the instrument. Therefore, we consider the possibility of observing the radiation deflected at an angle of ±3 arcmin from the rays coming from the center of symmetry. This is so called “offset angle”, labeled as φ. Two extreme rays that can fall on the crystal are marked as blue and red lines in the Fig. 10. They fall on the crystal at points with coordinates:

$$ x_{1}=r\,\cos\,(\theta_{1}-\varphi) $$

(2)

$$ y_{1}=r\,\sin\,(\theta_{1}-\varphi) $$

(3)

and

$$ x_{2}=r\,\cos\,(\theta_{2}+\varphi) $$

(4)

$$ y_{2}=r\,\sin\,(\theta_{2}+\varphi) $$

(5)

For a given type of crystal (i.e. specific crystal lattice spacing d), the offset angle φ, the detector length L and the desired wavelength range, our software determines the optimal geometry of the crystal–detector system. It calculates the crystal curvature, r , the positions of the edges of the crystal (x ₁,y ₁) and (x ₂,y ₂) and the positions of the edges of the detector (x ₃,y ₃) and (x ₄,y ₄).

Because we have nine unknowns we would need nine equations to uniquely solve the system. In addition to the (2–5) for a geometry shown in Fig. 10 we can write the following set of equation for the positions of the detector edges:

$$ y_{3}=a_{2}x_{3}+b_{2} $$

(6)

$$ y_{3}=a_{L}x_{3}+b_{L} $$

(7)

$$ y_{4}=a_{1}x_{4}+b_{1} $$

(8)

$$ y_{4}=a_{L}x_{4}+b_{L} $$

(9)

Here a ₁, b ₁, a ₂ and b ₂ are the coefficients (a- the slope, b- the y-intercept of the line in the form y = a x + b) of lines connecting the points of incidence of the extreme rays at the ends of the detector with the corresponding edges of the crystal. They can be established from the geometrical relationships between the angles in the system:

$$\begin{array}{@{}rcl@{}} a_{1}&=&\tan\,(\beta_{1})=\tan\,(2\theta_{1}-90^{\circ}-\varphi) \end{array} $$

(10)

$$\begin{array}{@{}rcl@{}} a_{2}&=&\tan\,(\beta_{2})=\tan\,(2\theta_{2}-90^{\circ}+\varphi) \end{array} $$

(11)

$$\begin{array}{@{}rcl@{}} b_{1}=y_{1}-x_{1}\, \tan\,(\beta_{1})&=&r\,\sin\,(\theta_{1}-\varphi)-r\,\cos\,(\theta_{1}-\varphi)\,\tan\,(2\theta_{1}-90^{\circ}-\varphi) \end{array} $$

(12)

$$\begin{array}{@{}rcl@{}} b_{2}=y_{2}-x_{2}\, \tan\,(\beta_{2})&=&r\,\sin\,(\theta_{2}+\varphi)-r\,\cos\,(\theta_{2}+\varphi)\,\tan\,(2\theta_{2}-90^{\circ}+\varphi) \end{array} $$

(13)

We have now eight equations, but we introduced two additional variables, a _L and b _L . Those coefficients define the straight line on which the detector lies. Thus three more equations are needed.

Firstly we can use the known length of the detector to write:

$$ L^{2}=(x_{4}-x_{3})^{2}+(y_{4}-y_{3})^{2} $$

(14)

For an optimal arrangement of the crystal – detector unit the angles δ between the extreme rays and the detector are the same (see: Fig. 10). Therefore we can write:

$$ \frac{a_{1}-a_{L}}{1+a_{1}a_{L}}=\frac{a_{L}-a_{2}}{1+a_{2}a_{L}} $$

(15)

Left and right sides of this equation are the expression on tangent of angle between detector and the extreme rays.

Due to the CCD’s housing we need some free space between the crystal and detector and so, we need to introduce p parameter- the distance between the closest part of the crystal and the detector. The last needed equation can be therefore written using this known parameter. Depending on the slope of the detector the equation may take one of the two forms:

$$ x_{4}=x_{1}+p $$

(16)

when the detector is positioned as shown in Fig. 10 (a _L >0), or

$$ x_{3}=x_{1}+p $$

(17)

When x ₃ is closer to the crystal than x ₄ (a _L <0).

Ultimately we have eleven unknown values and eleven equations (2–9, 14, 15 and one of 16 or 17) so the problem can be solve unambiguously. Minimalization of parameter p or equalization of angles δ, described by (15–17) can be treated as criteria for the optimization of the crystal–detector design but they are necessary for the closure of system of equations to be solved.

Firstly we determinate the radius of curvature. Starting with (14) we substitute the y ₃ and y ₄ into the (7) and (9). After transform we can write:

$$ {x_{4}^{2}}(1+{a_{L}^{2}})+x_{4}[-2x_{3}(1+{a_{L}^{2}})]+[x_{3}(1+{a_{L}^{2}})-L^{2}]=0 $$

(18)

which allow us to determinate the x ₄:

$$ x_{4}=x_{3}+S $$

(19)

Here:

$$ S=\pm\frac{\sqrt{(1+{a_{L}^{2}})L^{2}}}{(1+{a_{L}^{2}})} $$

(20)

On the other hand using the (6), (7), (8) and (9) we have:

$$ a_{1}x_{4}+b_{1}-a_{L}x_{4}=a_{2}x_{3}+b_{2}-a_{L}x_{3} $$

(21)

We can solve it for x ₃ and insert the (19) to get:

$$ x_{3}=\frac{b_{2}-b_{1}}{a_{1}-a_{2}}+S\frac{a_{L}-a_{1}}{a_{1}-a_{2}} $$

(22)

Now we can use appropriate (16) or (17) following by (12), (13) and (6) to obtain the relevant equations for crystal radius of curvature:

$$ r=\frac{p(a_{1}-a_{2})-S(a_{1}-a_{2})-S(a_{L}-a_{1})}{\sin\,(\theta_{2}+\varphi)-\sin\,(\theta_{1}-\varphi)-a_{2}\,\cos\,(\theta_{2}+\varphi)+a_{2}\,\cos\,(\theta_{1}-\varphi)} $$

(23)

$$ r=\frac{p(a_{1}-a_{2})-S(a_{L}-a_{1})}{\sin\,(\theta_{2}+\varphi)-\sin\,(\theta_{1}-\varphi)-a_{2}\,\cos\,(\theta_{2}+\varphi)+a_{2}\,\cos\,(\theta_{1}-\varphi)} $$

(24)

In the next step we solve the (15) with respect to variable a _L . It is a quadratic equation which gives us two solutions. But from (16) and (17) we know, that the (23) works for a _L >0 while the (24) works for a _L <0. This allow us to choose appropriate solution of (15) and use it in selected equation for r. In this way we get four values for crystal radius of curvature. From the possible solutions of (23) and (24) we choose those, for which the value of radius of curvature are positive (convex crystal) and calculate the corresponding crystal and detector positions (x ₃,y ₃) and (x ₄,y ₄). Finally we chose an arrangement that give as small as possible size of crystal–detector unit.

Now we need to solve an inverse task, i.e. to calculate wavelengths corresponding to each pixel (x,y) of the detector. Without loss of generality we can assume that X-rays of given wavelength fall on the crystal at the coordinates (x ₁,y ₁). Points (x ₁,y ₁) and (x,y) define straight line with a slope a:

$$ y-y_{1}=a(x-x_{1}) $$

(25)

Using (10) for a:

$$ a=\tan\,(2\theta-\varphi-90^{\circ})=-\frac{\cos\,(2\theta-\varphi)}{\sin\,(2\theta-\varphi)} $$

(26)

and (2) and (3) for x ₁ and y ₁, we can obtain:

$$ y-r\,\sin\,(\theta-\varphi)=-\frac{\cos\,(2\theta-\varphi)}{\sin\,(2\theta-\varphi)}[x-r\,\cos\,(\theta-\varphi)] $$

(27)

This equation can be transformed into:

$$ \begin{array}{ccc} 2\,\sin\,\theta \,\cos\,\theta(y\,\cos\,\varphi+x\,\sin\,\varphi)+2\,\cos^{2}\,\theta(x\,\cos\,\varphi-y\,\sin\,\varphi)-(x\,\cos\varphi-y\,\sin\,\varphi)\\ =2r\,\cos^{3}\,\theta \,\cos^{2}\,\varphi-r\,\cos\,\theta\, \cos^{2}\,\varphi+2\,\sin\,\theta\, \cos^{2}\,\theta \,\sin\,\varphi\, \cos\,\varphi+2r\,\sin\,\theta\, \cos^{2}\,\theta \,\sin\,\varphi \,\cos\,\varphi\\ -r\,\sin\,\theta \,\sin\,\varphi \,\cos\,\varphi+2r\,\sin^{2}\,\theta\, \cos\,\theta\, \sin^{2}\,\varphi\\ +2r\,\sin^{2}\,\theta \,\cos\,\theta\, \cos^{2}\,\varphi-2r\,\sin\,\theta\, \cos^{2}\,\theta \,\sin\,\varphi \,\cos\,\varphi\\ +r\,\sin\,\theta \,\cos\,\varphi \,\sin\,\varphi-2r\,\sin\,\theta \,\cos^{2}\,\theta \,\sin\,\varphi\, \cos\,\varphi+2r\,\cos^{3}\,\theta \,\sin^{2}\,\varphi-r\,\cos\,\theta\, \sin^{2}\,\varphi \end{array} $$

(28)

We introduce the designations:

$$ A=y\,\cos\,\varphi+x\,\sin\,\varphi $$

(29)

and

$$ B=x\,\cos\,\varphi-y\,\sin\,\varphi $$

(30)

After making the substitution and simplification we obtain the fourth degree equation:

$$ \cos^{4}\,\theta\,[4(A^{2}+B^{2})]+\cos^{3}\,\theta\,[-4rB]+\cos^{2}\,\theta\,[-4(A^{2}+B^{2})+r^{2}]+\cos\,\theta\,[2rB]+[B^{2}]\,=\,0 $$

(31)

which may be solved using the FZ_ROOTS function available in IDL. This allows us to calculate for a chosen crystal-detector arrangement the X-ray wavelength range that corresponds to every detector bin physical positions limits.

Appendix B: The flux determination

The Bragg law describes the X-rays diffraction on the crystal. Unfortunately this law does not describe the complicated Bragg diffraction-interference perfectly. In the “real” case, the monochromatic X-ray beam become scattered after “reflection” from the crystal. The crystal rocking curve (see Fig. 11 ) shows the dependence between the reflection angle and the reflectivity, R:

$$R=\frac{I_{0}}{I} $$

where I and I ₀ are the incident and diffracted fluxes respectively. The 𝜃−𝜃 ₀ is the difference between the real reflected angle and the angle resulting from the Bragg law. The rocking curve for perfect crystals in the Bragg case has been discussed by many authors. A list of references may be found in books [e.g. 20, 49] or in the articles [4, 17] or [6]. The characteristic features of the rocking curve are the full width at half maximum (FWHM), the peak reflectivity (P _c ) and the integral reflectivity (R _c ):

$$\begin{array}{@{}rcl@{}} R_{c}(\theta)&=&\int\,R(\theta)\,d\theta=\int\,R(\theta(\lambda))\,\frac{d\theta}{d\lambda}d\lambda\\ &=&\int\,R(\lambda)\,\frac{d\theta}{d\lambda}d\lambda=\int\,R(\lambda)\frac{1}{2d\, \cos\,\theta}\,d\lambda\approx\frac{1}{2d \,\cos\,\theta}\int\,R(\lambda)\,d\lambda\\ &=&\frac{1}{2d \,\cos\,\theta}R_{c}(\lambda)=\frac{\sin\,\theta}{2d \,\cos\,\theta\, \sin\,\theta}R_{c}(\lambda)=\frac{\text{tg}\,\theta}{\lambda}R_{c}(\lambda) \end{array} $$

(32)

Fig. 11

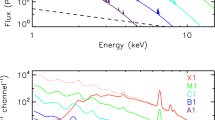
The rocking curve of the Si 111 bent crystal at energy 3800 eV (λ=3.26Å). It was obtained using XOP software [32]

Thus

$$ R_{c}(\lambda)=R_{c}(\theta)\lambda \text{ctg}\theta $$

(33)

To interpret the observing spectra we need to know the instrument response function, which will relate the rates [cts/s/bin] observed in each spectral bin into absolute fluxes units [photons/cm ²/s/Å]. Let us consider an infinitesimally small fragment of crystal of length dl in the dispersion plane and width W. This elements supplies the detector with the flux:

$$ dN=F E \,dA $$

(34)

here E is the efficiency function, that contain the instrument filters’ transmission function, the collimator transmission function and the detector efficiency. F is given by:

$$ F=\int\limits_{0}^{\infty} f(\lambda)R(\lambda)d\lambda $$

(35)

where f(λ) is the flux on-axis point source and R(λ) is the crystal reflectivity. d A is the area of the considered segment of crystal. For a point source on the line-of-sight we can write:

$$ dA=A_{0} \,\sin\,\theta=W\, dl\, \sin\,\theta $$

(36)

Because

$$ dl=rd\theta $$

(37)

and

$$ \frac{dl}{d\lambda}=\frac{r\, d\theta}{d\lambda}=\frac{r}{2d \,\cos\,\theta} $$

(38)

the area can be written as:

$$ dA=\frac{W \,r\, \sin\,\theta}{2d \,\cos\,\theta} d\lambda $$

(39)

We can therefore rewrite (34) as:

$$ dN=E \frac{W \,r\, \sin\,\theta}{2d\, \cos\,\theta} d\lambda \int\limits_{0}^{\infty} f(\lambda)R(\lambda)d\lambda $$

(40)

Equation (40) was used to calculate expected fluxes on the synthetic spectrum (see Fig. 4).