Abstract
The concept of an evidential conditional If A then C that can be defined by the conjunction of \(A>C\) and \(\lnot C > \lnot A\), where > is a conditional of the kind introduced by Stalnaker and Lewis, has recently been studied in a series of papers by Vincenzo Crupi and Andrea Iacona. In this paper I argue that Crupi and Iacona’s central idea that contraposition captures the idea of evidential support cannot be maintained. I give examples showing that contraposition is neither necessary nor sufficient for a conditional’s antecedent supporting its consequent. Crupi and Iacona’s alternative account of evidential conditionals that is based on a probabilistic measure of evidential support cannot add to the credentials of their modal account, because both the theoretical role of contraposition and the resulting logic are different in this account.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Evidential support and evidential conditionals
The notion of evidential support originated in the field of inductive logic or Bayesian confirmation theory. Carnap (1962, p. xvi) noted that the verb ‘to confirm’ is ambiguous between ‘to make firm’ and ‘to make firmer’, and he accordingly highlighted the difference between confirmation as firmness and confirmation as increase in firmness. Since Carnap, the discussion has been led mainly within a probabilistic framework, so the difference was often glossed as one between confirmation as establishing high posterior probability (above a specified threshold) and confirmation as raising the prior probability (being positively relevant). ‘Support’ is similarly ambiguous, but the notion of evidential support has acquired a fairly stable meaning by now, referring to the second of these readings. Evidence E lends evidential support to hypothesis H if and only if \(\textit{Pr}(H\big \vert E) > \textit{Pr}(H)\).Footnote 1 This sense of ‘raising the doxastic status’ is the sense I have in mind when I speak of evidential support. However, the main part of this paper is not about a probabilistic interpretation of the idea, but a modal interpretation in a possible worlds framework.
In a series of recent papers, Vincenzo Crupi and Andrea Iacona have advocated and put forward an analysis of the evidential conditional (EC). The idea is that in a conditional as used in natural language, the antecedent typically supports the consequent, or provides evidence or reasons for it. Other paraphrases—which Crupi and Iacona themselves do not use—talk of the antecedent as being (positively) relevant to the consequent, or of a connection or link between antecedent and consequent.
Crupi and Iacona actually introduced evidential conditionals twice over and provided a modal account as well as a probabilistic account of them. The modal account is introduced in Crupi and Iacona (2020). Together with Eric Raidl, they determined the logic of the evidential conditional and provided soundness and completeness proofs with respect to a possible worlds semantics (Raidl 2019, Raidl, Iacona & Crupi 2021). Crupi and Iacona (2022a) extend the modal approach to cover ‘concessive conditionals’ where the defining characteristic of ECs is absent. Very often, concessive conditionals feature the use of even if in the antecedent or of still in the consequent.Footnote 2 I applaud the suggestion that antecedents in (non-concessive) conditionals increase the firmness of the belief in the consequents. The central point of Crupi and Iacona’s modal account, however, is that evidential conditionals can be defined as conditionals that satisfy the formal scheme of contraposition. I briefly recount this idea in Sect. 2. In Sect. 3, I show that, contrary to what most examples given in the literature suggest, a violation of contraposition does not enforce a concessive reading of the conditionals involved. Then I show in Sects. 4 and 5 that the acceptance of the contrapositive is neither necessary nor sufficient for the acceptance of a conditional in which the antecedent supports the consequent. The probabilistic account of evidential conditionals is developed in Crupi and Iacona (2021, 2022b). While focussing mainly on Crupi and Iacona’s modal theory, I will comment on its relation to their probabilistic theory in Sect. 6. This theory relies on a particular way of encoding evidential relevance, but I argue that this fact is not suited for lending plausibility to their modal theory. If my arguments are correct, then Crupi and Iacona’s talk of the evidential conditional—that is, of a unique conditional which is modelled by both their modal and their probabilistic theoriesFootnote 3—is misleading. In Sect. 7, I conclude that satisfaction of contraposition has little to do with evidential support.
2 The Chrysippus Test according to Crupi and Iacona
Crupi and Iacona start out their explication of evidential conditionals referring to an incompatibility between the antecedent and the negated consequent of such conditionals. They take the term ‘incompatibility’ from Chrysippus, but caution the reader that ‘the word “incompatible” may be construed in different ways, and nobody knows what Chrysippus exactly had in mind.’ (2020, p. 5) They then offer their own interpretation:
The core idea of the evidential account is that a conditional \(A \vartriangleright C\) is true if and only if A and \(\lnot C\) are incompatible in the following sense: if A is true, then C cannot easily be false, and if C is false, then A cannot easily be true.Footnote 4
Crupi and Iacona then go on and analyse the first part of the quoted passage by the Ramsey Test for the suppositional conditional \(A>C\), and the second part by what they call the Reverse Ramsey Test for this conditional, which is identical with the ordinary Ramsey test for \(\lnot C>\lnot A\). This conjunction they call Chrysippus Test (Crupi & Iacona 2020, p. 5). Crupi and Iacona do not literally formulate their characterization of evidential conditionals in terms of suppositional conditionals (but see their Fact 22). However, since the Ramsey Test is designed to apply to suppositional conditionals, and the Reverse Ramsey Test is just the Ramsey Test for the contraposed suppositional conditional, the following representation of the evidential conditional is a good rendering of the essence of Crupi and Iacona’s idea.
-
(CT)
\(A \vartriangleright C\) is true\(^\textrm{A}\) iff both \(A>C\) and \(\lnot C > \lnot A\) are true\(^\textrm{A}\). Footnote 5
I do not want to commit myself to the view that conditionals have truth values, nor to the view that they have only acceptability or assertibility values. When I say that a conditional is true\(^\textrm{A}\), this may be taken literally as ‘true’, but it may also—especially in the context of discussions of confirmation or evidence—be interpreted as ‘accepted by the agent’. The conditional \(A>C\) should be read as If A, then C. It is intended to be an ordinary suppositional conditional of the kind that has been studied in conditional logic since the pioneering works of Stalnaker (1968) and Lewis (1973). \(A>C\) means, roughly, that AC-worlds are more possible (closer to the actual world or more plausible) than \(A\overline{C}\)-worlds, in symbols \(AC \prec A\overline{C}\).Footnote 6 I am using Lewis (1973) talk of ‘comparative possibility’ as a cover term for both metaphysical ‘closeness to the evaluation world’ and epistemic ‘plausibility’. Suppositional conditionals form the background of Crupi and Iacona’s theory of ECs. Crupi and Iacona presume that the meaning of suppositional conditionals can be analysed in terms of Lewis’s semantics based on systems of spheres of possible worlds. For this semantics, Lewis’s ‘official’ conditional logic VC is sound and complete. Thus suppositional conditionals satisfy the following principles:Footnote 7
(Ref) | A>A | Reflexivity |
(LLE) | If \(A > C\) and \(A \dashv \vdash B\), then \(B > C\). | Left Logical Equivalence |
(RW) | If \(A > B\) and \(B\vdash C\), then \(A > C\). | Right Weakening |
(And) | If \(A > B\) and \(A > C\), then \(A > B\wedge C\). | Conjunction in the Consequent |
(Or) | If \(A > C\) and \(B > C\), then \(A\vee B > C\). | Disjunction in the Antecedent |
(Cut) | If \(A\wedge B > C\) and \(A > B\), then \(A > C\). | Cautious Cut |
(CMon) | If \(A > C\) and \(A > B\), then \(A\wedge B > C\). | Cautious Monotonicity |
(NRat) | If \(A > C\) and not \(A\wedge \lnot B > C\), then \(A\wedge B > C\). | Negation Rationality |
(DRat) | If \(A\vee B > C\) and not \(A > C\), then \(B > C\). | Disjunctive Rationality |
(RMon) | If \(A > C\) and not \(A >\lnot B\), then \(A\wedge B > C\). | Rational Monotonicity |
Disjunctive Rationality follows, in the context of the more basic principles, from Rational Monotonicity (see Lehmann & Magidor 1992, p. 19). For this reason, it is usually not mentioned explicitly, but it is an interesting and important principle in conditional logic and neighbouring fields.Footnote 8 It will play a critical role in Sect. 6 below.
The most distinctive property of \(\vartriangleright\) is that it satisfies contraposition, essentially by definition. Two other very important properties are that it satisfies neither Strengthening of the Antecedent (aka Monotonicity) nor Weakening the Consequent (aka Right Weakening):
(Mon) | If \(A\vartriangleright C\) and \(B\vdash A\), then \(B\vartriangleright C\). | Strengthening the Antecedent |
(RW) | If \(A\vartriangleright C\) and \(C\vdash B\), then \(A\vartriangleright B\). | Weakening the Consequent |
(Mon) has been regarded as one of the paradigmatic invalidities of conditionals at least since the seminal works of Adams (1965), Stalnaker (1968) and Lewis (1973). (RW) was more recently suggested to be a paradigmatic invalidity (‘the hallmark’) of conditionals in which the antecedent is positively relevant for the consequent by Rott (2022, pp. 137, 153).
The Chrysippus Test says that an evidential conditional is true\(^\textrm{A}\) if the corresponding suppositional conditional and its contrapositive are true\(^\textrm{A}\). Crupi and Iacona contend that this test ‘seems required in order to preserve the intuition that A must support C’ and that it ‘characterizes the evidential interpretation’ according to which ‘a conditional is true just in case its antecedent provides evidence for its consequent’ (2020, pp. 2, 5).
3 Failure of Contraposition and Concessive Conditionals
Most counterexamples to contraposition that can be found in the literature are such that the premise conditional admits a concessive interpretation. Indeed, the classical works that started contemporary conditional logic feature examples of this kind. Adams emphasized that there is no valid inference from If it rains, the game will be played to If the game is not played, it will not have rained.Footnote 9 Stalnaker held that there is no valid inference from If the U.S. halts the bombing, then North Vietnam will not agree to negotiate to If North Vietnam agrees to negotiate, then the U.S. will not have halted the bombing.Footnote 10 Lewis pointed out that there is no valid inference from If Boris had gone to the party, Olga would still have gone to If Olga had not gone, Boris would still not have gone.Footnote 11
These examples start from conditionals If A, then C, in which A does not quite effect \(\lnot C\), but A at any rate goes some way towards bringing \(\lnot C\) about. Moreover, it is often plausible to assume that A is necessary for \(\lnot C\): a stop of the bombing, for example, is considered to be a necessary condition for the start of negotiations. Let us call such conditionals conditionals of insufficient reason.Footnote 12 A typical pattern of comparative possibility in such examples is \(\overline{A}C\preceq AC\prec A\overline{C}\prec \overline{A}\mkern1mu\overline{C}\), with \(\overline{A}\mkern1mu\overline{C}\) sometimes being completely impossible or unconceivable. This is indeed a situation in which Even if A, C may appropriately be asserted.
Like several authors before them, Crupi and Iacona suggest that violations of contraposition always involve concessive conditionals.Footnote 13 And the counterexamples and statements in the more recent literature seem to confirm this impression.Footnote 14 However, I want to show now that this impression is the result of a curiously lopsided selection of examples in the literature. The conclusion that evidential conditionals—which are different from concessive conditionals—never fail the scheme of contraposition is in fact unwarranted.
First of all, we verify in general terms that a violation of contraposition does not necessarily involve a premise conditional that can be interpreted as an even if conditional. A counterexample to contraposition (for suppositional conditionals) consists in a pairing of \(A>C\) and \(\lnot C \not > \lnot A\). This means that \(AC \prec A\overline{C}\) and \(\overline{A}\mkern1mu\overline{C}\not \prec A\overline{C}\). Call this the violation-of-contraposition situation.
Does it follow from the violation of contraposition that the premise \(A>C\) is a concessive conditional, i.e., roughly, that it can be read as an even if conditional? I answer this question by using Crupi and Iacona’s own theory of concessive conditionals. Being a novel theory, it still shares many traits with other proposals in the literature (cf. the careful discussion in Crupi and Iacona (2022a). I focus on two of them: (i) Even if A, C entails C, and (ii) Even if A, C entails the suppositional conditional If \(\lnot A\), then C (\(\lnot A>C\)).Footnote 15 Should a situation in which contraposition fails be compatible with the falsity\(^\textrm{A}\) of either C or If \(\lnot A\), then C, then clearly the premise \(A>C\) is not a concealed even if conditional.
So we ask, firstly: Does the violation-of-contraposition situation imply that the consequent C is true\(^\textrm{A}\)? Yes it does, if Rational Monotonicity is available.Footnote 16
Secondly, does the violation-of-contraposition situation imply that \(\lnot A>C\) is true\(^\textrm{A}\)? This conditional means that \(\overline{A}C \prec \overline{A}\mkern1mu\overline{C}\). But this relation is not entailed by the relations that characterise the violation of contraposition, as we can see in Fig. 1. The position of the \(\overline{A}C\)-worlds is entirely unconstrained by the failure of \(A>C\) to contrapose. The figures make clear visually that while the conditional \(\top >C\) is implied in the violation-of-contraposition situation, the conditional \(\lnot A>C\) is not implied. Only case (a) is compatible with an even if interpretation of \(A>C\),Footnote 17 cases (b) and (c) clearly aren’t.
Violation-of-contraposition situations with \(A>C\) and \(\lnot C \not > \lnot A\). Arrows are pointing downwards to more plausible worlds. Read the edge \(A\overline{C} \to AC\) as \(AC \prec A\overline{C}\). The negated edge \(A\overline{C}\)
 \(\overline{A}\mkern1mu\overline{C}\) should be understood as expressing \(\overline{A}\overline{C}\not \prec A\overline{C}\) It may be thought of as pointing either upwards or sideways. In red: potential positions of \(\overline{A}C\) in relation to \(\overline{A}\mkern1mu\overline{C}\)
\(\overline{A}\mkern1mu\overline{C}\) should be understood as expressing \(\overline{A}\overline{C}\not \prec A\overline{C}\) It may be thought of as pointing either upwards or sideways. In red: potential positions of \(\overline{A}C\) in relation to \(\overline{A}\mkern1mu\overline{C}\)
4 Contraposition is not Necessary for Support
The counterexamples against contraposition one can find in the literature are of just one type of situation in which contraposition fails. There are others. The following examples will be described in probabilistic terms. The conditionals (1) to (14) below are to be interpreted as suppositional conditionals that are accepted if the conditional probability of the consequent given the antecedent is ‘high enough’. An alternative, purely qualitative presentation would be possible, but I think it helps to derive the qualitative picture from the probabilistic one. In the transformations I will adopt the rough and simple rule that a (partial) possible world v is more plausible than another (partial) possible world w if and only if the probability of v is a lot higher (orders of magnitude higher as it were) than the probability of w. It will be easy to verify that the probabilities then transform into the weak orders on possible worlds I will specify. But nothing depends on the particular numbers used in the following examples. If greater discrepancies between probability values or higher threshold values for the acceptance of conditionals were desired, then the numbers could easily be adapted. Contraposition fails in situations that are commonly referred to when the base-rate fallacy is discussed. We take two well-known examples given by Tversky and Kahneman (1982) and Eddy (1982).
Example 1 (cabs). A cab was involved in a hit-and-run accident at night. Two cab companies operate in the city, the Green Company and the Blue Company, the former being much bigger than the latter. A witness is summoned before the court. She identifies the colour of cars with high reliability. For concreteness, assume that 85% of the cabs in town are green, 15% are blue, and that the reliability of the witness to identify car colours is 80%.Footnote 18 Writing g for The cab is green and \(w_g\) for The witness reports that the cab is green, we have \(\textit{Pr}(gw_g) = 68\%\), \(\textit{Pr}(g\overline{w_g}) = 17\%\), \(\textit{Pr}(\overline{g}\mkern1mu\overline{w_g}) = 12\%\) and \(\textit{Pr}(\overline{g}w_g) = 3\%\). A corresponding ordering of comparative possibility is this: \(gw_g\prec g\overline{w_g}\sim \overline{g}\mkern1mu\overline{w_g}\prec \overline{g}w_g\).
Now we want to know whether we accept
-
(1)
If the cab is green, then the witness identifies it as green.
as well as
-
(2)
If the witness does not identify the cab as green, then it isn’t green.
First we note that \(\textit{Pr}(w_g\big \vert g) = 0.8\) which we, for the sake of argument, take as high enough to warrant acceptance of the premise conditional (1). However, \(\textit{Pr}(\lnot g\big \vert \lnot w_g) = \frac{\textit{Pr}(\lnot g\wedge \lnot w_g)}{\textit{Pr}(\lnot w_g)} = \frac{0.12}{0.17\,+\,0.12} = 0.41\). So if the witness says the cab was blue (which, given common background knowledge, is equivalent to saying that it was not green), it is still more likely that it was in fact green than that is was blue. The conditional (2) is unacceptable. Contraposition fails. So (1) is not true\(^\textrm{A}\) if read in Crupi and Iacona’s evidential sense. Yet intuitively, the antecedent of the premise conditional (1) clearly supports its consequent. It is not an even if conditional.
Example 2 (tests). A certain diagnostic test identifies whether or not a patient has cancer with high reliability, and there is a huge preponderance of healthy people in the population considered. More concretely, there is a prior probability of 1% that a patient has cancer. The test diagnoses malignant cells correctly with a probability of 79.2%, and non-malignant cells correctly with a probability of 90.4%.Footnote 19 Writing c for The patient has cancer and n for The test comes out negative, we have \(\textit{Pr}(\overline{c}n) = 89.5\%\), \(\textit{Pr}(\overline{c}\mkern1mu\overline{n}) = 9.5\%\), \(\textit{Pr}(c\overline{n}) = 0.8\%\) and \(\textit{Pr}(cn) = 0.2\%\). A corresponding ordering of comparative possibility is this: \(\overline{c}n\prec \overline{c}\mkern1mu\overline{n}\prec c\overline{n}\prec cn\).
Now we want to know whether we accept
-
(3)
If a patient doesn’t have cancer, the test will come out negative.
as well as
-
(4)
If the test does not come out negative, the patient has cancer.
\(\textit{Pr}(n\big \vert \lnot c) = 0.904\) which is high enough to warrant acceptance of the premise conditional(3). However, \(\textit{Pr}(c\big \vert \lnot n) = \frac{\textit{Pr}(c\wedge \lnot n)}{\textit{Pr}(\lnot n)} = \frac{0.008}{0.008\,+\,0.095} = 0.078\). So if the test is positive, it is still very unlikely that the patient has cancer. Conditional (4) is unacceptable, contraposition fails. So (3) is not true\(^\textrm{A}\) if read in Crupi and Iacona’s evidential sense. Yet again, the antecedent of the premise conditional (3) supports its consequent. It is not an even if conditional.
Let us look at two more examples that have nothing to do with perception and testing and are not taken from the literature about base-rate fallacies.
Example 3 (baleful disease). An infectious disease breaks out with millions of cases, and a treatment has been developed to combat the disease. More than 95% of the infected people are administered the treatment, and more than 90% of the patients treated recover. However, more than 90% of the persons without treatment don’t recover. With t for treatment and r for recovery, let us use assume for concreteness that the probabilities are \(\textit{Pr}(tr) = 88\%\), \(\textit{Pr}(t\overline{r}) = 8.7\%\), \(\textit{Pr}(\overline{t}\mkern1mu\overline{r}) = 3\%\) and \(\textit{Pr}(\overline{t}r) = 0.3\%\). A corresponding ordering of comparative possibility is this: \(tr\prec t\overline{r}\sim \overline{t}\mkern1mu\overline{r}\prec \overline{t}r\).
Now suppose we know that Ann contracted the disease, but we don’t know whether she has received the treatment. We have good reasons to say:
-
(5)
If Ann has received the treatment, she recovers.
The fact that Ann received the treatment would clearly support, or be evidence for, the fact that she recovers. It would also make recovery very likely. Now, is it appropriate to assert
-
(6)
If Ann doesn’t recover, she hasn’t received the treatment.
in this scenario? No, because almost three quarters of the people who don’t recover did in fact get the treatment. So contraposition fails. Yet again, the antecedent of the premise conditional (5) clearly supports its consequent. It is not an even if conditional.Footnote 20
Example 4 (project). Pam, an experienced and dedicated researcher, has just started working on a project, and for this reason the project is likely to be successful. If she were missing, the project might fail. But it is not impossible that Pam will not perform well and the project fails. With p for Pam works on the project and s for The project is successful, an ordering of comparative possibility reflecting the situation is this: \(ps\prec p\overline{s}\sim \overline{p}\mkern1mu\overline{s}\sim \overline{p}s\).
We can say
-
(7)
If Pam works on the project, the project will be successful.
but we are not justified to say
-
(8)
If the project is not successful, Pam has not worked on the project.
Thus contraposition fails. But again, the antecedent of the premise conditional (7) clearly supports its consequent. It is not an even if conditional.Footnote 21
For contraposition to fail, the only thing that matters is the pattern of probabilities or comparative similarities. The patterns we need to make our point are ubiquitous. Examples 1–3 may be subsumed under case (c) of Fig. 1, \(AC\prec A\overline{C}\preceq \overline{A}\mkern1mu\overline{C}\prec \overline{A}C\), where Examples 1 and 3 have a tie and Example 2 has a strict preference in the middle. Example 4 is an instantiation of case (b) of Fig. 1. Taken together, these examples illustrate well that not all conditionals in which the antecedent supports the consequent contrapose. Contraposition is not necessary for support.
5 Contraposition is not Sufficient for Support
Now I try to show that contraposition is not sufficient for conditionals that are meant to encode the idea of evidential support. We’ll be content with two examples here.
Example 5 (tricky cabs). The scenario begins like Example 1 above, but some of the figures are different: 85% of the cabs in town are green, 15% are blue. The witness identifies the green colour of cabs with a high reliability of 83.5%. But this time she is apt to mistake blue cabs for green ones under the relevant circumstances (the night was moonless, and the blue of the cabs borders on turquoise). This mistake in fact occurs in 80% of the cases under similar circumstances. For concreteness, let us assume that the probabilities are \(\textit{Pr}(gw_g) = 71\%\), \(\textit{Pr}(g\overline{w_g}) = 14\%\), \(\textit{Pr}(\overline{g}w_g) = 12\%\) and \(\textit{Pr}(\overline{g}\mkern1mu\overline{w_g}) = 3\%\). A corresponding ordering of comparative possibility is this: \(gw_g\prec g\overline{w_g}\sim \overline{g}w_g\prec \overline{g}\mkern1mu\overline{w_g}\).
In this scenario not only
-
(9)
If the cab is not green, then the witness identifies it as green.
is acceptable (using the probability threshold of 0.8 which we accepted for the sake of argument in Example 1), but its contrapositive
-
(10)
If the witness does not identify the cab as green, then it is green.
is equally acceptable, since \(\textit{Pr}(g\big \vert \lnot w_g) = \frac{\textit{Pr}(g\wedge \lnot w_g)}{\textit{Pr}(\lnot w_g)} = \frac{0.14}{0.14\,+\,0.03} = 0.82\). However, contrary to the analysis of Crupi and Iacona, this does not mean that the premise conditional (9) is a truly evidential one. Even though the witness has some perceptual troubles, the cab’s not being green still lowers the probability that he reports green. Intuitively, the antecedent of (9) clearly fails to support its consequent. It has the likings of an even if conditional.
Moreover, Crupi and Iacona’s analysis of even if conditionals has it that
-
(11)
If the cab is green, then the witness identifies it as green.
is a concessive conditional. But this is counterintuitive, too, since a cab’s being green increases its chance of getting reported as green, if only slightly.
Example 6 (benign disease). The scenario begins like Example 3 above, only some of the figures are different: more than 93% of the infected people are administered the treatment, and more than 94% of the patients treated recover. The big difference is that this time the disease is rather benign, so that almost 91% of the persons who have not been treated recover, too. For concreteness, let us assume that the probabilities are \(\textit{Pr}(tr) = 88\%\), \(\textit{Pr}(t\overline{r}) = 5.4\%\), \(\textit{Pr}(\overline{t}r) = 6\%\) and \(\textit{Pr}(\overline{t}\mkern1mu\overline{r}) = 0.6\%\). A corresponding ordering of comparative possibility is this: \(tr\prec t\overline{r}\sim \overline{t}r\prec \overline{t}\mkern1mu\overline{r}\).
Suppose we know that Ann contracted the disease, but we don’t know whether she has received the treatment. Are we are ready to assert the conditional
-
(12)
If Ann hasn't received the treatment, she recovers.
in this scenario? It is very likely that Ann recovers, but not receiving the treatment would not support her recovery. Considering the figures, not getting the treatment would in fact be slightly unfavourable to her recovery. In as far as we feel justified in asserting (12), it is not an evidential conditional, but rather more like an even if conditional. Still, contraposition works here:
-
(13)
If Ann doesn’t recover, she has (still) received the treatment.
The explanation for this lies in the particular figures of the case: the contraposed conditional (13) is acceptable because it is extremely unlikely that Ann is an untreated patient who doesn’t recover. But (13), too, has an even if flavour, since we can equally well say
-
(14)
If Ann recovers, she has received the treatment.
Crupi and Iacona’s modal analysis predicts that If \(\lnot t\), r is an evidential and If t, r is a concessive conditional. Both claims are counterintuitive here.
For the presence or absence of evidential support, the only thing that matters is the pattern of probabilities or comparative similarities. It is easy to come by a pattern that is suitable to make our point. In Examples 5 and 6, the pattern is \(\overline{A}C\prec \overline{A}\mkern1mu\overline{C}\sim AC\prec A\overline{C}\), where A and C are the antecedent and the consequent of the contraposing conditional. These examples illustrate well that not all contraposing conditionals are such that the antecedent supports the consequent. Contraposition is not sufficient for support.
The examples in this and the previous section make it clear, I think, that whether or not the contrapositive of a true\(^\textrm{A}\) suppositional conditional is true\(^\textrm{A}\), too, does not depend on the issue of whether this suppositional conditional expresses a relation of evidential support between its antecedent and its consequent.
6 The Probabilistic Interpretation of Evidential Conditionals
So far I have focussed on Crupi and Iacona’s modal approach. The authors point out, however, that there is an alternative approach to ECs that they call ‘a probabilistic version of the evidential account’ (Raidl, Iacona & Crupi 2021, p. 2). They have cross-references between the two accounts in each of their relevant papers,Footnote 22 and it is clear that they see a confluence of ideas and results leading to a mutual reinforcement of their alternative accounts.
The probabilistic semantics for evidential conditionals is developed in ‘Three Ways of Being Non-material’ (Crupi & Iacona, 2022b). The authors first define a valuation which is supposed to represent the degree of assertibility of an evidential conditional:
The principal case in the uppermost line uses the so-called Rips measure of argument strength (Rips, 2001); the first term is intuitive as a measure of relative increase in firmness, the second term makes it immediately evident that the contrapositive \(\lnot C \vartriangleright \lnot A\) gets the same valuation as \(A\vartriangleright C\).Footnote 23 Crupi and Iacona call \(\textit{U}_{\textit{Pr}}(A\vartriangleright C) = 1 - \textit{V}_{\textit{Pr}}(A\vartriangleright C) = \textit{V}_{\textit{Pr}}(\lnot (A\vartriangleright C))\) the ‘uncertainty’ of \(A\vartriangleright C\), which they identify with its lack of assertibility.
Secondly, Crupi and Iacona employ Ernest Adams’s uncertainty sum rule to define logical validity, substituting their V-values for Adams’s conditional probabilities: An inference scheme is valid if and only if the uncertainty of the conclusion does not exceed the sum of the uncertainties of the premises for any probability function \(\Pr\).Footnote 24 Finally they check whether the probabilistic EC’s thus interpreted validate or invalidate the items of a rather long list of candidate principles.
Of the principles for conditionals we listed in Sect. 2, Crupi and Iacona (2022b) prove that their probabilistic interpretation of evidential conditional validates (Ref), (LLE), (And), (Or), (CMon) and (NRat), but it does not validate (RW), (Cut) and (RMon) (all with ‘\(\vartriangleright\)’ substituted for ‘>’). When introducing their modal account, Crupi and Iacona (2020) mentioned only few of these principles, namely (Ref), (LLE) and (RW). The validity of the principles (And), (Or) and (CMon) was verified by 2019, the validity of (NRat) and the invalidity of (Cut) and (RMon) by Rott (2020). The surprising finding was that the modal account and the probabilistic account validate exactly the same subset of this set of principles. Characteristically, both accounts also validate contraposition. Crupi and Iacona checked a few more conditions, and here, too, the modal and the probabilistic accounts exhibit the same pattern of validities and invalidities.Footnote 25 All together, this is a list of about 15 principles that all come out the same in Crupi and Iacona’s modal and probabilistic accounts. This observation is indeed striking.
Crupi & Iacona (2020, p. 23) conclude that the EC based on the probabilistic semantics ‘implies exactly the same pattern of results’ as the EC based on the modal semantics, and that the ‘probabilistic semantics [...] converges with the modal semantics [...] in all relevant respects’ (2022a, note 30).
Given that contraposition has long been supposed to be a paradigmatically invalid inference scheme for conditionals, Crupi and Iacona’s ECs are interesting in that they show what a logic of conditionals satisfying contraposition can look like, and the logic obtained is indeed surprisingly well-behaved. Thus such conditionals are a very nice object of logical research. My question here, however, is whether the probabilistic analysis lends support to Crupi and Iacona’s modal analysis of conditionals expressing evidential support. I think that the answer must be negative, for essentially two reasons.
First, it is useful to get clear about the interplay of the Rips measure and contraposition. The Rips measure was used in the seminal paper of Crupi, Crupi et al. (2007) as one half of their preferred measure of inductive support, the z-measure. The authors followed a general strategy of mirroring symmetries which ended up highlighting contraposition as a central feature. Crupi & Tentori (2013, p. 365) wanted to revive the ‘old and illustrious idea [... that] inductive logic should parallel the deductive model by providing a generalized, quantitative theory of partial entailment’. Of course, the validity of contraposition is an important characteristic of deductive reasoning. But deduction has many other characteristics (Tarski, for one, highlighted reflexivity, transitivity and monotonicity), so one may wonder why it is just contraposition that should be respected.
In any case, it is important to keep in mind that the Rips measure is itself a measure of evidential support. It is positive if and only if \(\textit{Pr}(C\big \vert A) > \textit{Pr}(C)\). So it respects Carnap’s notion of increase in firmness. Crupi and Tentori (and Gonzalez) employed contraposition as a normative requirement that singles out the z-measure from a large number of measures of evidential support, all of which may lay claim to capturing the increase-in-firmness idea.Footnote 26 Among these measures of relevance confirmation, as they are sometimes called, contraposition helped to recommend a unique ‘best’ one: the z-measure was selected essentially because it is the same for \(A\vartriangleright C\) and \(\lnot C \vartriangleright \lnot A\) and thus validates contraposition. But the theoretical role of contraposition in the probabilistic context was not at all linked to the representation of evidential support.
As we saw above, this is completely different for Crupi and Iacona’s modal account of evidential conditionals. Here there is no predefined collection of candidates that all embody the notion of confirmation as increase in firmness. It is contraposition itself that is supposed to capture this notion. I have argued above that contraposition is not suitable for this purpose.
Second, each of the principles explicitly checked by Crupi and Iacona, is valid (or invalid) with respect to the modal semantics if and only if it is valid (respectively invalid) with respect to the probabilistic semantics. So Crupi and Iacona have considerable inductive evidence for their claim that the two kinds of semantics generate the same logic. However, even a long list of common validities and invalidities is no proof that two logics are identical. And in fact it can be shown that they aren’t. Crupi and Iacona’s modal and probabilistic accounts can be seen to come apart if we consider the principle of Disjunctive Rationality, which we listed in Sect. 2 above.
-
Disjunctive Rationality is validated by the modal account. Proof: Suppose that \(A\vee B\vartriangleright C\) and not \(A\vartriangleright C\). That is (a) \(A\vee B>C\), (b) \(\lnot C>\lnot (A\vee B)\), and either (c) not \(A>C\) or (d) not \(\lnot C>\lnot A\). By (RW) for >, (b) excludes (d), so (c) is the case. From (a) and (c), it follows that \(B>C\), by (DRat) for >. From (b), it follows that \(\lnot C>\lnot B\), by (RW) for >. But now we have shown that \(B\vartriangleright C\).Footnote 27
-
However, Disjunctive Rationality is invalid on the probabilistic account, as can be seen from the following counterexample. Consider two probabilistically independent propositions p and q that are randomly true or false, and a third proposition r such that r is very probable when exactly one of p and q is given, and r is very improbable otherwise. In numbers, let the probability distribution \(\textit{Pr}\) be given by \(\textit{Pr}(p\wedge q\wedge \lnot r) = \textit{Pr}(p\wedge \lnot q\wedge r) = \textit{Pr}(\lnot p\wedge q\wedge r) = \textit{Pr}(\lnot p\wedge \lnot q\wedge \lnot r) = 0.24\) and \(\textit{Pr}(p\wedge q\wedge r) = \textit{Pr}(p\wedge \lnot q\wedge \lnot r) = \textit{Pr}(\lnot p\wedge q\wedge \lnot r) = \textit{Pr}(\lnot p\wedge \lnot q\wedge r) = 0.01\). Then \(\textit{Pr}(r) = \textit{Pr}(r\big \vert p) = \textit{Pr}(r\big \vert q) = 0.5\) and \(\textit{Pr}(r\big \vert p\vee q) = \nicefrac {49}{75} = 0.65\) (last number rounded). We are interested in the inference from \((p\vee q)\vartriangleright r\) and \(\lnot (p\vartriangleright r)\) to \(q\vartriangleright r\). Crupi and Iacona’s assertibility values are \(V((p\vee q)\vartriangleright r) = \nicefrac {(0.65-0.5)}{(1-0.5)} = 0.3\) and \(V(p\vartriangleright r) = V(q\vartriangleright r) = 0\), which gives us the uncertainty values \(U((p\vee q)\vartriangleright r) = 0.7\), \(U(\lnot (p\vartriangleright r)) = 0\) and \(U(q\vartriangleright r) = 1\). But this means that the uncertainty of the conclusion of this instance of Disjunctive Rationality (\(=1\)) is greater than the sum of the uncertainties of its premises (\(=0.7+0\)).
The same discrepancy concerns a dual principle that may be called ‘Conjunctive Rationality’:
-
(CRat)
If \(A\vartriangleright B\wedge C\) and not \(A\vartriangleright B\), then \(A\vartriangleright C\).
This is a weakening of (RW) that is valid on Crupi and Iacona’s modal account, but invalid on their probabilistic account of evidential conditionals.Footnote 28 (CRat) plays an important role as an axiom for difference-making conditionals in Rott (2022).
Thus it turns out that Crupi and Iacona have characterized two distinct ‘evidential conditionals’ that are governed by two similar, but different logics. Which one represents the true meaning of evidential support? Should Disjunctive Rationality be validated or shouldn’t it? Do we have reason to favour the probabilistic account (and thus reject Disjunctive Rationality), because this account is based on the Rips measure that is clearly an encoding of the idea of evidential support? I will leave these questions unanswered. It remains a striking discovery of Crupi and Iacona that the logics of the two kinds of evidential conditional are similar. But as my first worry above indicates, this fact, far from substantiating the claim that contraposition encodes evidential support, is itself in need of explanation.
7 Conclusion
I have criticized the thesis that conditionals expressing a relation of evidential support between the antecedent and the consequent are conditionals that satisfy contraposition.Footnote 29 First I showed that a violation of contraposition does not imply an even if reading of its premise. Using a variety of examples, I have then argued that the fact that a conditional is true or accepted along with its contrapositive is neither necessary nor sufficient for its antecedent supporting the consequence. None of these examples is in any way exotic. They all exhibit a pattern of probabilities that is instantiated in countless real-life situations. An account that handles all the examples given in this paper correctly is offered by Rott (2022). Lest this paper be deemed entirely negative, a few comparative thoughts on Rott’s difference-making conditionals are added in an appendix to this paper.
The idea that contraposition captures evidential support may have been engendered by two infelicitous inductive generalizations. First, the fact that the counterexamples to contraposition prominent in the literature involve as premises conditionals with a strong even if flavour suggested that every violation of contraposition must involve such conditionals. And second, the fact that Crupi and Iacona’s modal account and their probabilistic account result in the same pattern of validities among the principles they checked suggested that the two kinds of conditionals are governed by the same logic. The induction bases were indeed quite good, with about ten examples in the first case, and one or two dozens of inference schemes in the second. As we have seen, however, both generalizations are incorrect. There are good counterexamples against contraposition that do not start from even if conditionals, and there are logical principles that are valid on Crupi and Iacona’s modal and invalid on their probabilistic account.
We have long become used to the fact that conditionals as used in natural language appear to be non-monotonic, i.e., that they don’t satisfy Strengthening the Antecedent. Why should they satisfy contraposition? Why should conditionals be geared towards passing the ‘Chrysippus Test’? A compelling argument is needed to answer these questions and substantiate the claim that contraposition is a formal representation of the intuitive ideas of evidence and support. If my arguments in this paper are correct, the prospects for finding such an argument are dim.Footnote 30
Change history
27 January 2023
A Correction to this paper has been published: https://doi.org/10.1007/s10670-022-00651-6
Notes
This is equivalent to \(\textit{Pr}(H\big \vert E) > \textit{Pr}(H\big \vert \lnot E)\). I neglect the role of a ‘background theory’ on which everything would need to be conditionalized.
To keep things reasonably simple, I identify concessive conditionals with even if conditionals in this paper, knowing well that this is an idealization. I also take it that if ... still conditionals are equivalent to even if conditionals.
Crupi & Iacona (2020, p. 4), notation adapted.
On the meaning of Chrysippus’ conditional, the authors thus disagree with Sanford (1989, pp. 68–69) who stated: ‘[Clarence Irving] Lewis’s account of strict implication is ... as close as it can be to the account of the conditional we attribute to Chrysippus.’ According to Lenzen (2021), the Chrysippian conditional is stronger than the stict conditional in that it also asserts the separate possibility of both A and \(\lnot C\).
\(\preceq\) is presumed to be a weak order on the set of possible worlds, with \(\prec\) as its asymmetric and \(\sim\) its symmetric part (indicating a tie). In line with the tradition, ‘\(x\prec y\)’ means ‘x is closer to the evaluation world than y’ or ‘x is more(!) plausible than y.’ The expression ‘\(AC \prec A\overline{C}\)’ can be read in two ways. Either we think of it as a relation between partial possible worlds (only very few facts are represented) that are identified with valuations. Or it is a relation between propositions (sets of full possible worlds consisting of very many facts) stating that for every world satisfying \(A\wedge \lnot C\) there is a closer/more plausible world satisfying \(A\wedge C\).
My formulation of the principles is phrased in the metalanguage, without embeddings of conditionals, in order to make consistent place for the view that conditionals don’t have truth values. The symbol \(\vdash\) denotes logical implication with respect to a Tarskian background logic, the symbol \(\dashv \vdash\) denotes mutual implication.
Stalnaker (1968, p. 107). The reader is asked to assume that a halt in the bombing is not sufficient to bring the North Vietnamese to the negotiating table, but much more, like a complete withdrawal of U.S. troops, is required to achieve this.
Lewis (1973, p. 35). Lewis asks the reader to suppose that Boris stayed away solely in order to avoid Olga. Notice that the word ‘still’ occurs in the consequents of both conditionals, so they are explicitly marked as concessive conditionals.
Here I am picking up a term of Gomes (2019, p. 55).
Entailment (i) was first advocated by Pollock (1975, pp. 52–53), entailment (ii) by Gärdenfors (1981, p. 209). (ii) is part of Crupi and Iacona’s analysis of even if, according to which the logical form of a concessive Even if A, C is a conjunction \((A>C)\wedge (\lnot A>C)\wedge (\lnot C>A)\). (i) is a consequence of this analysis. See Crupi & Iacona (2022a, pp. 12–15).
Let us prove this claim. First we note that for semantic reasons, the truth\(^\textrm{A}\) of C is equivalent to the truth\(^\textrm{A}\) of \(\top >C\) (with \(\top\) denoting a tautology). So we show that \(\top >C\) is implied in violation-of-contraposition situations. Suppose that \(A>C\) and not \(\lnot C>\lnot A\). From \(A>C\), we get \(A > \lnot A\vee C\), by (RW), and we also have \(\lnot A > \lnot A\vee C\), by (Ref) and (RW). So by (Or) and (LLE), we get \(\top > \lnot A\vee C\). From not \(\lnot C>\lnot A\), we get not \(\top \wedge \lnot C>\lnot A\vee C\), by (LLE), (Ref), (And) and (RW). But in the presence of \(\top > \lnot A\vee C\), the latter can only happen if \(\top >C\), by (RMon).—If Rational Monotonicity were not available, the consequent C might fail to be true\(^\textrm{A}\) in a violation-of-contraposition situation.
A prototypical even if situation is \(\overline{A}C \prec AC \prec A\overline{C}\prec \overline{A}\mkern1mu\overline{C}\), with a ‘large distance’ between \(\overline{A}C\) and \(\overline{A}\mkern1mu\overline{C}\).
These are Tversky & Kahneman’s (1982, pp. 156–158) figures.
The figures are taken from Eddy (1982, pp. 252–254).
This example and Example 6 below are variants of examples given in Rott (2020, p. 13).
This example is taken from Rott (2022, p. 148).
Note that \(\textit{Pr}(C\big \vert A) \ge \textit{Pr}(C)\) iff \(\textit{Pr}(\lnot A\big \vert \lnot C) \ge \textit{Pr}(\lnot A)\).
See Adams (1975, pp. 2, 18–19, 57–58). It is not self-evident that Crupi and Iacona’s U-values really express uncertainties and that it makes sense to transfer the Adamsian uncertainty sum rule for the definition of validity from conditional probabilities to Crupi and Iacona’s valuations. No justification for this move is offered by Crupi and Iacona.
For example, Modus Ponens and Material Implication are valid, Conjunctive Sufficiency is invalid.
The validity of (CRat) for the modal account is verified in Rott (2020, p. 7). Its invalidity for the probabilistic account can be gathered from the counterexample just given. We have \(V(\lnot r\vartriangleright (\lnot p\wedge \lnot q))=0.3\) (number rounded) and \(V(\lnot r\vartriangleright \lnot p) = V(\lnot r\vartriangleright \lnot q) = 0\) and proceed exactly as in the case of Disjunctive Rationality.
Crupi and Iacona’s modal account was criticized earlier by Rott (2020).
In the modal framework, this is not the same as saying that the consequent is (accepted as) true on the supposition that A but not (accepted as) true on no or a tautological supposition. The basic idea of difference-making conditionals is similar to that of Joyce’s and Christensen’s probative measure of evidential support, \(\textit{Pr}(C\big \vert A)\,-\,\textit{Pr}(C\big \vert \lnot A)\), which deviates from the more common difference measure, \(\textit{Pr}(C\big \vert A)\,-\,\textit{Pr}(C)\). ‘Old evidence’, i.e., an antecedent that is already accepted as true, may well evidentially support the consequent. Cf. Joyce (1999, pp. 203–213), Christensen (1999, pp. 444–452), Hájek and Joyce (2008, pp. 121–124) and Rott (2022, pp. 139–140).
It is called the ‘Strong Ramsey Test’ in Rott (1986). Rott works within the framework of belief revision theory. Raidl (2021) shows how to convert the analysis into a modal logic framework.— Rott (2022) characterizes yet another kind of conditional called dependence conditional and definable by A
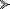 C iff \(A>C\) and \(\lnot A > \lnot C\). It must not be confused with the conditional defined by the similarly-looking Chrysippus Test (CT).
C iff \(A>C\) and \(\lnot A > \lnot C\). It must not be confused with the conditional defined by the similarly-looking Chrysippus Test (CT).
References
Adams, E. W. (1965). The logic of conditionals. Inquiry, 8, 166–197.
Adams, E. W. (1975). The logic of conditionals. Dordrecht: Reidel.
Bennett, J. (2003). A philosophical guide to conditionals. Oxford: Oxford University Press.
Berto, F., & Özgün, A. (2021). Indicative conditionals: Probabilities and relevance. Philosophical Studies, 178(11), 3697–3730.
Carnap, R. (1962). Logical foundations of probability. Chicago: University of Chicago Press. (Second, revised edition)
Christensen, D. (1999). Measuring confirmation. Journal of Philosophy, 96(9), 437–461.
Crupi, V., & Iacona, A. (2022a). On the logical form of concessive conditionals. Journal of Philosophical Logic, 51(3), 633–651.
Crupi, V., & Iacona, A. (2020). The evidential conditional. Erkenntnis. https://doi.org/10.1007/s10670-020-00332-2.
Crupi, V., & Iacona, A. (2021). Probability, evidential support, and the logic of conditionals. Argumenta, 6(2), 211–222.
Crupi, V., & Iacona, A. (2022b). Three ways of being non-material. Studia Logica, 110(1), 47–93.
Crupi, V., & Tentori, K. (2013). Confirmation as partial entailment: A representation theorem in inductive logic. Journal of Applied Logic, 11(4), 364–372.
Crupi, V., Tentori, K., & Gonzalez, M. (2007). On Bayesian measures of evidential support: Theoretical and empirical issues. Philosophy of Science, 74(2), 229–252.
Douven, I. (2016). The epistemology of indicative conditionals: Formal and empirical approaches. Cambridge: Cambridge University Press.
Eddy, D. M. (1982). Probabilistic reasoning in clinical medicine: Problems and opportunities. In D. Kahneman, P. Slovic, & A. Tversky (Eds.), Judgment under uncertainty: Heuristics and biases (pp. 249–267). Cambridge: Cambridge University Press.
Freund, M. (1993). Injective models and disjunctive relations. Journal of Logic and Computation, 3(3), 231–247.
Gärdenfors, P. (1981). An epistemic approach to conditionals. American Philosophical Quarterly, 18(3), 203–211.
Gomes, G. (2019). Meaning-preserving contraposition of natural language conditionals. Journal of Pragmatics, 152, 46–60.
Hájek, A., & Joyce, J. M. (2008). Confirmation. In S. Psillos & M. Curd (eds.), Routledge companion to philosophy of science (pp. 115-128). London: Routledge. (Second edition 2013, pp. 146–159)
Jackson, F. (1979). On assertion and indicative conditionals. Philosophical Review, 88, 565–589.
Jackson, F. (1991). Introduction. In F. Jackson (Ed.), Conditionals (pp. 1–7). Oxford: Clarendon Press.
Joyce, J. M. (1999). The foundations of causal decision theory. Cambridge: Cambridge University Press.
Lehmann, D., & Magidor, M. (1992). What does a conditional knowledge base entail? Artificial Intelligence, 55(1), 1–60.
Lenzen, W. (2021). The third and the fourth stoic account of conditionals. In I. Sedlar & M. Blicha (Eds.), Logica yearbook 2020 (pp. 127–146). College Publications.
Lewis, D. (1973). Counterfactuals. Oxford: Blackwell.
Lycan, W. G. (2001). Real conditionals. Oxford: Oxford.
Merin, A. (2021). Evidential relevance. In M. Knauff & W. Spohn (Eds.), Handbook of rationality (pp. 265–275). Cambridge, Mass.: MIT Press.
Pollock, J. (1975). Four kinds of conditionals. American Philosophical Quarterly, 12(1), 51–59.
Raidl, E. (2019). Quick completeness for the evidential conditional. Retrieved from http:// philsci-archive.pitt.edu/16664 (Manuscript of 27 November 2019)
Raidl, E., Iacona, A. & Crupi, V. (2021). The logic of the evidential conditional. Review of Symbolic Logic. (Published online 8 March 2021)
Raidl, E. (2021). Definable conditionals. Topoi, 40(1), 87–105.
Rips, L. (2001). Two kinds of reasoning. Psychological Science, 12, 129–134.
Rott, H. (2020). Notes on contraposing conditionals. Retrieved from http://philsciarchive. pitt.edu/17092 (Manuscript of 19 April 2020)
Rott, H. (1986). Ifs, though and because. Erkenntnis, 25(3), 345–370.
Rott, H. (2014). Three floors for the theory of theory change. In V. Punčochář & M. Dančák (Eds.), Logica Yearbook 2013 (pp. 187–205). London: College Publications.
Rott, H. (2022). Difference-making conditionals and the relevant Ramsey test. Review of Symbolic Logic, 15(1), 133–164.
Sanford, D. H. (1989). If P, then Q: Conditionals and the foundations of reasoning. London: Routledge.
Sprenger, J., & Hartmann, S. (2019). Bayesian philosophy of science. Oxford: Oxford University Press.
Stalnaker, R. (1968). A theory of conditionals. In N. Rescher (Ed.), Studies in logical theory (Vol. 2, pp. 98–112). Oxford: Blackwell.
Tversky, A., & Kahneman, D. (1982). Evidential impact of base rates. In D. Kahneman, P. Slovic, & A. Tversky (Eds.), Judgment under uncertainty: Heuristics and biases (pp. 153–160). Cambridge: Cambridge University Press.
Acknowledgements
I would like to thank Jake Chandler, Vincenzo Crupi, Andrea Iacona, and in particular Eric Raidl and two anonymous referees of Erkenntnis for comments on precursors of this paper. Part of this work was supported by the Deutsche Forschungsgemeinschaft, project number RO 1219/12-1.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this article was revised: In the original publication of the article, the below first principle has been missed to include under the section 2. (Ref) A>A Reflexivity
Appendix. Comparison with difference-making conditionals
Appendix. Comparison with difference-making conditionals
Suppositional conditionals may be thought of as conforming to Carnap’s notion of firmness. On supposing the antecedent, the consequent is (accepted as) true. How can we encode Carnap’s notion of increase in firmness? The obvious idea is to say that without supposing the antecedent the consequent is not (accepted as) true. Both ideas can be combined by the rule that a conditional If A then C is (accepted or) true if and only if the consequent is (accepted as) true on the supposition that A but not when no supposition is made. A very similar idea is explored in Rott (2022). His difference-making conditionals are defined by the rule that If A then C is (accepted or) true if and only if C is (accepted as) true on the supposition that A is true but not on the supposition that A is false.Footnote 31 We can express this by making use of suppositional conditionals:
-
(DMC)
\(A \gg C\) iff \(A>C\) and not \(\lnot A > C\).
Rott calls this idea the ‘Relevant Ramsey Test’.Footnote 32
The conditionals \(A\gg C\) and \(A\vartriangleright C\) make logically independent statements, neither one implies the other. This can be recognized easily from Fig. 2. The left part of this figure covers examples 1–4 above, its right part covers examples 5–6. The difference-making conditionals get our intuitions right in these cases. This suggests that they are a better fit for the notion of support than Crupi and Iacona’s evidential conditionals (on the modal account).Footnote 33
Constraints imposed on relations between possible worlds by evidential conditionals and difference making conditionals. The left branches of the two cases are identical, the right branches feature opposite relations. (For instructions how to read these diagrams, see Fig. 1.)
The rationale for difference-making conditionals is distinct from that of Crupi and Iacona’s evidential conditionals. Suppose that A logically implies C. This is sufficient for making the evidential conditional \(A\vartriangleright C\) true. In a sense, A certainly supports C. For the difference-making conditional, however, A needs to be a reason that makes a difference for C. If an agent believes C anyway, even on the assumption of \(\lnot A\), she would not accept \(A\gg C\). While evidential conditionals of the form \(A\vartriangleright \top\) (with \(\top\) denoting a tautology) are universally true or accepted, difference-making conditionals of the form \(A\gg \top\) are universally false or rejected. No tautology needs evidential support from any other proposition, no increase in firmness can be achieved by making any supposition.
Like evidential conditionals, difference-making conditionals importantly invalidate Right Weakening as well as Conjunctive Sufficiency (also known as ‘Conjunction Conditionalisation’ or ‘And-to-If Inference’). This is not to be regarded as bad behaviour, the violation of (RW) was even called ‘the hallmark’ of difference-making and relevance. Difference-making conditionals and ECs also agree in validating (And) and (CRat) and in invalidating (Cut) and (RMon). Evidential conditionals additionally validate (Ref), (Or), (CMon), (NRat) and, on the modal account, (DRat). Difference-making conditionals do not satisfy these principles, but only counterparts using de-relevantised conditionals (with the exception of (Ref)). Crupi and Iacona’s evidential conditionals thus validate more familiar logical principles than difference-making conditionals, and their logic is indeed nice. But this fact does not make up for their not capturing the notion they are supposed to capture.
I close with a remark on the principle of Disjunctive Rationality which played a critical role in Sect. 6 and is invalid for difference-making conditionals. First of all, we note that there are good counterexamples against Negation Rationality for \(\gg\). If Anne accepts his invitation, Ben will be happy does not imply either If Anne accepts his invitation and the current number of inhabitants of Berlin is odd, Ben will be happy or If Anne accepts his invitation and the current number of inhabitants of Berlin is even, Ben will be happy. Assuming (LLE), this is also a good counterexample against (DRat). Direct counterexamples against Disjunctive Rationality are more difficult to come by. Cases of overdetermination may afford suitable examples. Consider a small firing squad consisting of two soldiers only. Applying the difference-making analysis to the typical situation (in which a single shot is lethal), we should accept If the first or the second soldier fires, the convict will die, but we should accept neither If the first soldier fires, the convict will die nor If the second soldier fires, the convict will die. The firing of each soldier, taken individually, does not make a difference to the outcome of this gruelling scenario. It seems, however, that the two simpler conditionals are rather unassertable than unacceptable.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rott, H. Evidential Support and Contraposition. Erkenn 89, 2253–2271 (2024). https://doi.org/10.1007/s10670-022-00628-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10670-022-00628-5




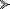 C iff
C iff 