A Compartmental Model for Stable Time-Dependent Modeling of Surface Water and Groundwater

Abstract

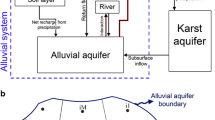
Water resource system planners make decisions that guide water management policy. The fundamental tools for assessing management and infrastructure strategies are combined hydro-economic models of river basins (RBHE models). These models have improved the economic efficiency of water use in situations of competition for scarce water resources. In RBHE models, a groundwater model is coupled with surface water models of the various water resources. Today, the groundwater models used in an RBHE model can be of two types: cell models or numerical models. Cell models are easy to use, but they are too simple to realistically describe the geology and hydrology of the area under investigation. Numerical models, in contrast, are closer to the physical behavior of the aquifer. However, the vast quantity of data to be analyzed makes them impractical for many management scenarios. Moreover, the calibrations of these high-resolution models are generally difficult and sensitive to the variation of parameters, especially when boundary conditions are dynamic. This is the case when dynamic river data or dynamic surface lake data are present. In this work, a compartmental cell model is built on the hydrogeology of the aquifer. In this approach, the hydrogeology of the aquifer and the dynamic boundary conditions are treated with separate models. A general mathematical formulation is presented where the calibration stage, the validation stage, and the prediction stage are formulated as a series of sub-model calibrations and solved using a general least squares routine. With this approach, it becomes possible to treat both the water level and the pumping rate in each cell as variables to be predicted. In most of the models, the pumping rates are known and the goals of the computation are to estimate the groundwater level. However, when for political or technical reasons access to some of the wells is difficult, the pumping rates are only partially known. Then, both groundwater levels and pumping rates are variables to be predicted by the groundwater model. A computer program was developed using MATLAB, with a Visual Basic graphical user interface using COM technology to access the advanced mathematical libraries. The approach was implemented with a real case study of the Yarkon–Taninim aquifer in Israel. The results indicate that the method is more stable than the classical approach.

Appendices

Appendix 1: List of Unknowns and Time S\eries in the Different Runs

In the present model, the unknown variables for each cell may be whether the water level and/or the pumping rate. In this appendix, we present for the different scenarios the list of unknown for each cell and the list of known time series data.

In the following tables, we summarized the unknown variables for the two scenarios presented.

1.1 List of Unknown Variables and Time Series for the Prediction Runs of Scenario 1

Scenario 1
Cell name	Water level series for the prediction period, data (m)	Pumping rates for the prediction period (mcm, 106 m3/year)
210CUP	Unknown	Known
210PUP	Unknown	Known
210PDO	Unknown	Known
211PDO	Unknown	Known
211CUP	Unknown	Known
211CDO	Unknown	Known
211PUP	Unknown	Known
214S	Unknown	Known
212S	Unknown	Known
220CUP	Unknown	Known
220PUP	Unknown	Known
220CDO	Unknown	Known
220PDO	Unknown	Known
230CUP	Unknown	Known
230PUP	Unknown	Known

1.2 List of Unknown Variables and Time Series for the Prediction Runs of Scenario 2

Scenario 2
Cell name	Water level series for the prediction period, data (m)	Pumping rates for the prediction period (mcm, 106 m3/year)
210CUP	Unknown	Known
210PUP	Known	Unknown
210PDO	Unknown	Known
211PDO	Known	Unknown
211CUP	Unknown	Known
211CDO	Unknown	Known
211PUP	Known	Unknown
214S	Unknown	Known
212S	Unknown	Known
220CUP	Unknown	Known
220PUP	Known	Unknown
220CDO	Unknown	Known
220PDO	Known	Unknown
230CUP	Unknown	Known
230PUP	Known	Unknown

Appendix 2: Algorithms Used for the Calibration, Validation, and Prediction Procedures

2.1 Algorithm for the Calibration Procedure

For each Cell _i , we have a number of ${N^i}_p$ to calibrate such that:

$$ {N_p} = \sum\limits_{{i = 1}}^{{i = {N_{{\text c} }}}} {{N^i}_p} \, $$

(8)

where N _p is the total number of parameters to calibrate.

For each Cell _i , the set of parameters to calibrate may be: ${P^i}_1,{P^i}_2, \cdots, {P^i}_{{N_{{\text p} }^i}}$

where

$P_l^i = {S_i}$ :

is the storativity of Cell _i , or

$P_l^i = {K_{{ij}}}$ :

is the hydraulic conductivity of water between Cell _i and Cell _j

$P_l^i = {K_{{lj}}}$ :

is the hydraulic conductivity of water between Cell _i and external resources

$P_l^i = {\alpha_i}$ :

is the replenishment parameter

The steps of the calibration process are:

• Step 1: Definition of the calibration vector

• We arrange the unknown parameters in the following order:

  $$ \overrightarrow {{K^T}} = \left[ {P_1^1,P_2^1, \cdots, P_{{N_{{\text P} }^1}}^1,P_1^2,P_2^2, \cdots, P_{{N_{{\text P} }^2}}^2, \cdots, P_1^{{{N_{{\text c} }}}},P_2^{{{N_{{\text c} }}}}, \cdots, P_{{N_{{\text P} }^{{{N_{{\text c} }}}}}}^{{{N_{{\text c} }}}}} \right] $$

  (9)

• Step 2: Building the calibration matrix

  The calibration matrix equation is given by:

  $$ M\overrightarrow K = \overrightarrow L $$

  (10)

  The size of the matrix M is ${N_p} \times {N_c} \times {N_y}$ (where N _y is the number of years for the calibration period and N _p for the unknown parameters).

  The size of $\overrightarrow L$ is ${N_c} \times {N_{{\text y} }}$.

  In the present model, the recharge, pumping, and spring discharge are given data for the period of calibration. Therefore, the second member, $\overrightarrow L$, for each cell Cell _i at time t is defined as:

  $$ L_i^{{t + \Delta t}} = \Delta t[{D^{{t + \Delta t}}}_i - {P^{{t + \Delta t}}}_i - {B_i}^{{t + \Delta t}}] + G_i^t $$

  (11)

  $G_i^t$ Represents the known part of Eq. 6 and $M_{{ij}}^t$ is described in Table 6.

  For a given parameter, there are three possibilities:

  • (a) The hydrological connection does not exist and therefore no value is assigned to the parameter.

  • (b) The hydrological connection exists and the value of the parameter is known. In this case, a new term is added to the right-hand side of the equation in a new value, $G_i^t$. This value is described in the last column of Table 6 for the various parameters.

  • (c) The hydrological connection exists and the value is unknown. Then this value is determined by the calibration process. A new term is added to the $M_{{ij}}^t$ matrix.

  This value is described in the second column of Table 6 for the various parameters.

• Step 3: Computation of the matrix system

  $$ M\overrightarrow K = \overrightarrow S $$

  The matrix M is not invertible, so we use the least squares method for the solution of this system. The difficulties are the constraints on the parameters.

Table 6 Calibration of parameters

The least squares solution of Eq. 2 may be obtained by various algorithms such as multi-regression analysis, SVD, and others. The use of MATLAB software provides access to a large library of algorithms which can each be tested in order to determine which one is the most efficient.

2.2 Algorithm for the Validation

The goal of the model validation is to measure the differences between the data and the results of the model in a time period different from the calibration period.

The matrix system for the validation at time t is given by the matrix equation:

$$ \overrightarrow {AH} = \overrightarrow R $$

(12)

where $\overrightarrow {{H^T}} = \left[ {h_1^{{t + \Delta t}},h_2^{{t + \Delta t}}, \cdots, h_{{{N_{{\text c} }}}}^{{t + \Delta t}}} \right]$

The size of the matrix A is ${N_c} \times {N_{{\text c} }}$; the size of the vector $\overrightarrow R$ is N _c.

Computations of the matrix A and the vector $\overrightarrow R$ are done for a given Cell _i at a given time t.

$$ \begin{gathered} {A_{{ii}}} = {S_i} + \sum\limits_{{j \in {S_i}}} {{T_{{ij}}}} + \sum\limits_{{l \in {E_i}}} {{T_{{lj}}}}; \hfill \\ i \ne j {A_{{ij}}} = - {T_{{ij}}}; \hfill \\ {R_i} = {S_i}{h^t}_i + \sum\limits_{{l \in {E_i}}} {{T_{{lj}}}{h_l}^{{t + \Delta t}}} + \Delta t[{N^{{t + \Delta t}}}_i + {D^{{t + \Delta t}}}_i - {P^{{t + \Delta t}}}_i - {B_i}^{{t + \Delta t}}] \hfill \\ \end{gathered} $$

(13)

2.3 Algorithm for the Prediction

The general prediction problem for a cell model may be formulated in two different ways:

Assumption 1: “For any cell, the unknown may be either the pumping rate or the hydraulic head, but not both of them and at least one of them.”

Then, define N _c as the cell number.

$$ \begin{gathered} C = \{ 1,2, \cdots, {N_c}\} \hfill \\ \hfill \\ \end{gathered} $$

Define the following sets of indices:

$$ \begin{gathered} H = \left\{ {j \in C, h_j^{{t + \Delta t}}{\text is} unknown} \right\} \hfill \\ Q = \left\{ {j \in C, {Q_j}{\text is} unknown} \right\} \hfill \\ \end{gathered} $$

$$ {N_H} = {\text Card} H; {N_Q} = {\text Card} Q; {N_c} = {N_H} + {N_Q} $$

2.3.1 Steps for the prediction process

Step 1: Definition of the prediction vector

$$ \overrightarrow {{U^T}} = \left[ {u_1^{{t + \Delta t}},u_2^{{t + \Delta t}}, \cdots, u_{{{N_c}}}^{{t + \Delta t}}} \right] $$

(14)

The size of matrix B is ${N_{{\text c} }} \times {N_c}; The size of vector \overrightarrow R is Nc.$

The unknown vector is built in the following order

$$ \begin{gathered} \operatorname{if} \,\,\,i \leqslant {N_{H}};\,u_{i}^{{t + \Delta t}} = h_{{\operatorname{l} (i)}}^{{t + \Delta t}}; \hfill \\ \operatorname{if} i > {N_{H}};\,u_{i}^{{t + \Delta t}} = Q_{{\operatorname{p} (i)}}^{{t + \Delta t}} \hfill \\ \end{gathered} $$

(15)

The index of the unknown head in the general system is $l(i){\kern 1pt} {\kern 1pt} \in {\kern 1pt} H$, and $p\left( i \right) \in Q$ is the index of the unknown pumping rate.

Step 2: Building the matrix

The linear system to solve for the prediction system for each new prediction year:

$$ E\overrightarrow U = \overrightarrow Z $$

(16)

The matrix E is defined as follows:

$$ \begin{gathered} \operatorname{if} \,i \in C; \hfill \\ j \leqslant {N_{H}};\,{E_{{ij}}} = {A_{{il(j)}}}; \hfill \\ j > {N_{H}};\,{E_{{ij}}} = 0;\operatorname{if} \,p(j) \ne i \hfill \\ {E_{{ij}}} = \Delta t\,{A_{{\operatorname{p} (j)}}};\,\operatorname{if} \,p(j) = i \hfill \\ \end{gathered} $$

(17)

The vector $\overrightarrow Z$ is defined as:

$$ \begin{gathered} \forall \,i \in \,C; \hfill \\ \operatorname{if} \,i \in H;{z_{i}} = {S_{i}}{h^{t}}_{i} + \sum\limits_{{l \in \,{E_{i}}}} {{T_{{lj}}}{h_{l}}^{{t + \Delta t}}} + \Delta t[{N^{{t + \Delta t}}}_{i} + {D^{{t + \Delta t}}}_{i} - {P^{{t + \Delta t}}}_{i} - {B_{i}}^{{t + \Delta t}}] \hfill \\ \operatorname{if} \,i \in Q;\,\operatorname{for} \,all\,j \in C{z_{j}} = {S_{j}}{h^{t}}_{j} + \sum\limits_{{l \in {\kern 1pt} {E_{i}}}} {{T_{{lj}}}{h_{l}}^{{t + \Delta t}}} + \Delta t[{N^{{t + \Delta t}}}_{i} + {D^{{t + \Delta t}}}_{i} - {B_{i}}^{{t + \Delta t}}] + {T_{{ij}}}h_{i}^{{t + \Delta t}} \hfill \\ \end{gathered} $$

(18)

Step 3: Solve $E\overrightarrow U = \overrightarrow Z$ (Eq. 16). With the MATLAB software, this matrix problem can be solved using the least squares algorithm.

Assumption 2: “For any cell, the unknown may be either the pumping rate or the hydraulic head, but also both of them or either one of them.”

Then, define N _p as the total number of unknowns.

$$ C = \left\{ {1,2, \cdots ,{N_{p}}} \right\} $$

Define the following sets of indices

$$ \begin{gathered} H = \left\{ {j \in C,h_{j}^{{t + \Delta t}}\operatorname{is} \,unknown} \right\} \hfill \\ Q = \left\{ {j \in C,{Q_{j}}\operatorname{is} \,unknown} \right\} \hfill \\ \end{gathered} $$

$$ {N_{H}} = \operatorname{Card} {\kern 1pt} H;{\kern 1pt} {N_{Q}} = \operatorname{Card} \,Q;{N_{c}} \ne {N_{H}} + {N_{Q}} $$