The long time scales of the climate–economy feedback and the climatic cost of growth

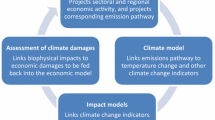
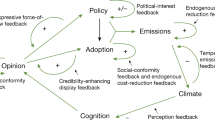
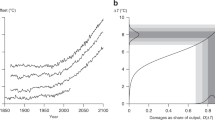
This paper is based on the perception that the inertia of climate and socio-economic systems are key parameters in the climate change issue. In a first part, it develops and implements a new approach based on a simple integrated model with a particular focus on an innovative transient impact and adaptation modeling. In a second part, a climate–economy feedback is defined and characterized. The following results were found. 1) It has a long characteristic time, which lies between 50 and 100 years depending on the hypotheses; this time scale is long when compared to the system's other time scales, and the feedback cannot act as a natural damping process of climate change. 2) Mitigation has to be anticipated since the feedback of an emission reduction on the economy can be significant only after a 20-year delay and is really efficient only after at least 50 years. 3) Even discounted, production changes due to an action on emissions are significant over more than one century. 4) The methodology of the Intergovernmental Panel on Climate Change (IPCC), which neglects the feedback from impacts to emissions, is acceptable up to 2100, whatever is the level of impacts. This analysis allows also to define a climatic cost of growth as the additional climate change damages due to the additional emissions linked to economic growth.

Appendices

Appendix A: The transfer evolution formalism A.1 Tangent linear system analysis

As explained in the article, the model is mathematically represented by a set of equations of two kinds:

• 1. cells:

  $$\begin{array}{*{20}l} {{\frac{{\partial \eta _{\alpha } }}{{\partial t}} = G_{\alpha } {\left( {\eta _{\alpha } ,\varphi _{1} ,\varphi _{2} , \ldots } \right)}} \hfill} \\ {{\frac{{\partial \eta _{\beta } }}{{\partial t}} = G_{\beta } {\left( {\eta _{\beta } ,\varphi _{1} ,\varphi _{2} , \ldots } \right)}} \hfill} \\ { \ldots \hfill} \\ \end{array} $$

  (A‐1)

• 2. transfers:

  $$\begin{array}{*{20}l} {{\varphi _{1} = f_{1} {\left( {\eta _{\alpha } ,\eta _{\beta } , \ldots ,\varphi } \right)}} \hfill} \\ {{\varphi _{2} = f_{2} {\left( {\eta _{\alpha } ,\eta _{\beta } , \ldots ,\varphi } \right)}} \hfill} \\ { \ldots \hfill} \\ \end{array} $$

  (A‐2)

Let η be the state vector of the complete system and φ be the vector of the dependent boundary conditions. With initial conditions at time t ₀, the system is a well-posed problem.

The method consists in building the first-order development of the dynamical system around its current state⁸ [η(t _n )]. For each cell α, it reads:

$$\frac{{\partial \eta _{\alpha } {\left( t \right)}}}{{\partial t}} = \frac{{\partial {\left( {\eta _{\alpha } {\left( {t_{n} } \right)} + \delta \eta _{\alpha } {\left( t \right)}} \right)}}}{{\partial t}} = G_{\alpha } {\left( {\eta _{\alpha } {\left( {t_{n} } \right)},\varphi {\left( {t_{n} } \right)}} \right)} + {\left( {\underline{\underline {\frac{{\partial G_{\alpha } }}{{\partial \eta _{\alpha } }}}} } \right)}{\left( {\eta _{\alpha } {\left( {t_{n} } \right)},\varphi {\left( {t_{n} } \right)}} \right)}\delta \eta _{\alpha } {\left( t \right)} + {\left( {\underline{\underline {\frac{{\partial G_{\alpha } }}{{\partial \varphi }}}} } \right)}{\left( {\eta _{\alpha } {\left( {t_{n} } \right)},\varphi {\left( {t_{n} } \right)}} \right)}\delta \varphi {\left( t \right)} + {\user1{\mathcal{O}}}{\left( {{\left( {t - t_{n} } \right)}^{2} } \right)}$$

(A‐3)

where $\delta \eta _{\alpha } {\left( t \right)} = \eta _{\alpha } {\left( t \right)} - \eta _{\alpha } {\left( {t_{n} } \right)}$ and δφ(t) = φ(t) − φ(t _n ).

The tangent linear system (TLS) corresponding to system (A-3) is, for each cell α:

$$\left\{ {\begin{array}{*{20}c} {{\frac{{\partial {\mathop \delta \limits^ \circ }\eta _{\alpha } {\left( t \right)}}}{{\partial t}} = G_{\alpha } \left| {_{{t_{n} }} } \right. + \left. {\underline{\underline {\frac{{\partial G_{\alpha } }}{{\partial \eta _{\alpha } }}}} } \right|_{{t_{n} }} {\mathop \delta \limits^ \circ }\eta _{\alpha } {\left( t \right)} + \left. {\underline{\underline {\frac{{\partial G_{\alpha } }}{{\partial \varphi }}}} } \right|_{{t_{n} }} {\mathop \delta \limits^ \circ }\varphi {\left( t \right)}}} \\ {{{\mathop \delta \limits^ \circ }\varphi {\left( t \right)} = {\sum\nolimits_\beta {\left. {\underline{\underline {\frac{{\partial f}}{{\partial \eta _{\beta } }}}} } \right|_{{t_{n} }} {\mathop \delta \limits^ \circ }\eta _{\beta } {\left( t \right)} + \left. {\underline{\underline {\frac{{\partial f}}{{\partial \varphi }}}} } \right|_{{t_{n} }} {\mathop \delta \limits^ \circ }\varphi {\left( t \right)}} }}} \\ \end{array} } \right.$$

(A‐4)

where the suffix β sweeps the list of subdomains.

We approximate the true time evolution of the model ${\left( {\delta \eta _{\alpha } {\left( t \right)}{\text{ }}and{\text{ }}\delta \varphi {\left( t \right)}} \right)}$ by ${\mathop \delta \limits^ \circ }\eta _{\alpha } {\left( t \right)}$ and ${\mathop \delta \limits^ \circ }\varphi {\left( t \right)}$, the TLS solutions, respectively, since they differ only by ${\user1{\mathcal{O}}}{\left( {{\left( {t - t_{n} } \right)}^{2} } \right)}$.

In formulation (A-4), the Jacobian matrices appear to contain critical information for the analysis of the interactions between variables. The TLS can be solved by various methods, including Laplace transforms. Rather than Laplace transformation, we shall use the more convenient Borel transformation defined by:

$$f{\left( t \right)}\xrightarrow{{\user1{\mathcal{B}}}}{\user1{\mathcal{B}}}{\left[ f \right]}{\left( \tau \right)} = \frac{1}{\tau }{\int_0^\infty {{\text{e}}^{{ - t \mathord{\left/ {\vphantom {t \tau }} \right. \kern-\nulldelimiterspace} \tau }} f{\left( t \right)}\operatorname{d} t} } = \frac{1}{\tau }\widetilde{f}{\left( {\frac{1}{\tau }} \right)}$$

(A‐5)

where $\widetilde{f}{\left( p \right)}$ stands for the Laplace transform of f(t). Contrary to the Laplace variable, the Borel variable τ is real and homogeneous with time.

Because ${\user1{\mathcal{B}}}{\left[ {{\partial f} \mathord{\left/ {\vphantom {{\partial f} {\partial t}}} \right. \kern-\nulldelimiterspace} {\partial t}} \right]} = {\left( {1 \mathord{\left/ {\vphantom {1 \tau }} \right. \kern-\nulldelimiterspace} \tau } \right)}{\user1{\mathcal{B}}}{\left[ f \right]}$, the Borel transform of equation (A-4) reads:

$$\left\{ {\begin{array}{*{20}c} {{{\user1{\mathcal{B}}}{\left[ {{\mathop \delta \limits^ \circ }\eta _{\alpha } } \right]} = {\overbrace {{\left[ {\left. {1 - \tau \underline{\underline {\frac{{\partial G_{\alpha } }}{{\partial \eta _{\alpha } }}}} } \right|_{{t_{n} }} } \right]}^{{ - 1}} \tau G_{\alpha } \left| {_{{t_{n} }} } \right.}^{{\user1{\mathcal{B}}}{\left[ {{\mathop \delta \limits^ \circ }\eta _{{\alpha ,{\text{dec}}}} } \right]}}} + {\overbrace {\tau {\left[ {\left. {1 - \tau \underline{\underline {\frac{{\partial G_{\alpha } }}{{\partial \eta _{\alpha } }}}} } \right|_{{t_{n} }} } \right]}^{{ - 1}} \left. {\underline{\underline {\frac{{\partial G_{\alpha } }}{{\partial \varphi }}}} } \right|_{{t_{n} }} }^{\underline{\underline {\user1{\mathcal{F}}}} }}{\user1{\mathcal{B}}}{\left[ {{\mathop \delta \limits^ \circ }\varphi } \right]}}} \\ {{{\user1{\mathcal{B}}}{\left[ {{\mathop \delta \limits^ \circ }\varphi } \right]} = {\sum\nolimits_\beta {\left. {\underline{\underline {\frac{{\partial f}}{{\partial \eta _{\beta } }}}} } \right|_{{t_{n} }} {\user1{\mathcal{B}}}{\left[ {{\mathop \delta \limits^ \circ }\eta _{\beta } } \right]} + \left. {\underline{\underline {\frac{{\partial f}}{{\partial \varphi }}}} } \right|_{{t_{n} }} {\user1{\mathcal{B}}}{\left[ {{\mathop \delta \limits^ \circ }\varphi } \right]}} }}} \\ \end{array} } \right.$$

(A‐6)

If the cell variables ${\mathop \delta \limits^ \circ }\eta$ are eliminated from the second equation, the complete system of equations (which includes cells) becomes:

$$\left\{ {\begin{array}{*{20}c} {{{\user1{\mathcal{B}}}{\left[ {{\mathop \delta \limits^ \circ }\eta } \right]} = {\user1{\mathcal{B}}}{\left[ {{\mathop \delta \limits^ \circ }\eta _{{{\text{dec}}}} } \right]} + \underline{\underline {\user1{\mathcal{F}}}} {\user1{\mathcal{B}}}{\left[ {{\mathop \delta \limits^ \circ }\varphi } \right]}}} \\ {{{\left[ {1 + \underline{\underline {\user1{\mathcal{C}}}} } \right]}{\user1{\mathcal{B}}}{\left[ {{\mathop \delta \limits^ \circ }\varphi } \right]} = {\user1{\mathcal{B}}}{\left[ {{\mathop \delta \limits^ \circ }\varphi _{{{\text{ins}}}} } \right]}}} \\ \end{array} } \right.$$

(A‐7)

where the quantities ${\user1{\mathcal{B}}}{\left[ {{\mathop \delta \limits^ \circ }\eta _{{{\text{dec}}}} } \right]}$, $\underline{\underline {\user1{\mathcal{F}}}}$, $\underline{\underline {\user1{\mathcal{C}}}}$ and ${\user1{\mathcal{B}}}{\left[ {{\mathop \delta \limits^ \circ }\varphi _{{{\text{ins}}}} } \right]}$depend onτ and can be calculated from the elementary Jacobian matrices and vectors at time t _n .

The first equation of (A-7) describes the evolution of the state variables. The state variables evolve because 1) of their internal inertial evolutions ${{\mathop \delta \limits^ \circ }\eta _{{{\text{dec}}}} }$ (which would be obtained if transfer models were changed to constant transfer model with ${\mathop \delta \limits^ \circ }\varphi = 0$) and 2) of the evolution of their boundary conditions ${\left( {{\mathop \delta \limits^ \circ }\varphi \ne 0} \right)}$. The matrix $\underline{\underline {\user1{\mathcal{F}}}}$ describes the influence of transfer variables on state variables and independently of the type of model used for these transfers ($\underline{\underline {\user1{\mathcal{F}}}}$ is independent of the model of ${\mathop \delta \limits^ \circ }\varphi$).

In the second equation, ${\mathop \delta \limits^ \circ }\varphi _{{{\text{ins}}}}$ represents the variation of transfer variables if ${\mathop \delta \limits^ \circ }\eta = {\mathop \delta \limits^ \circ }\eta _{{{\text{dec}}}}$ (i.e., if the cell models were changed to decoupled models with $\underline{\underline {\user1{\mathcal{F}}}} = 0$). Consequently, $\underline{\underline {\user1{\mathcal{C}}}}$ represents the effect of cell and transfer coupling.

The developed expression of the matrix $\underline{\underline {\user1{\mathcal{C}}}}$ shows how the partial derivatives defined at the cell and transfer level combine. The coefficients of the coupling matrix are rational fractions of the variable τ. This is the way the full dynamic of the system bounds the remaining variables after an elimination process.

Numerical solution of the transfer evolution formalism

For large systems, the above matrices are huge and sparseand exhibit an internal structure that depends upon the connections between cells and transfers. The full algorithm of the ZOOM⁹solver follows a technique called ‘relaxed supernodes hyper multifrontal method’ (cf. [23]). We focus here on the principles of the resolution that explain how the system dynamics is described by the coupling coefficients.

Equivalence between Borel transform and the Crank–Nicolson scheme

It is easily shown that the Crank–Nicolson resolution of the system (A-4) with a time step δt is identical to its Borel transform (A-7), with the correspondence $\tau \leftrightarrow \frac{{\delta t}}{2}$.

To demonstrate this equivalence, let $\widehat{\delta }X$ be the time evolution of variable X approximated by a Crank–Nicolson scheme, and consider the linear system:

$$\frac{{\partial \eta {\left( t \right)}}}{{\partial t}} = A\eta {\left( t \right)}$$

(A‐8)

If η(t) = η ₀ + δη(t), with δη(0) = 0, it may be rewritten as:

$$\frac{{\partial {\left( {\eta _{0} + \delta \eta {\left( t \right)}} \right)}}}{{\partial t}} = A{\left( {\eta _{0} + \delta \eta {\left( t \right)}} \right)}$$

(A‐9)

If a Crank–Nicolson scheme is applied to system (A‐9), with a time step δt, the discretized equation reads:

$$\frac{{\widehat{\delta }\eta {\left( {\delta t} \right)}}}{{\delta t}} = A\frac{1}{2}{\left( {2\eta _{0} + \widehat{\delta }\eta {\left( {\delta t} \right)}} \right)}$$

(A‐10)

which gives the time evolution of η, since $\widehat{\delta }\eta {\left( {\delta t} \right)} \approx \delta \eta {\left( {\delta t} \right)}$ for small δt.

For any t > 0, $\widehat{\delta }\eta {\left( t \right)}$ is given by:

$$\widehat{\delta }\eta {\left( t \right)} = {\left( {1 - \frac{t}{2}A} \right)}^{{ - 1}} A\eta _{0} t$$

(A‐11)

Now, the Borel transform of system (A-9) reads:

$$\begin{array}{*{20}c} {{\user1{\mathcal{B}}}{\left( {\frac{{\partial \delta \eta {\left( t \right)}}}{{\partial t}}} \right)} = \frac{1}{\tau }{\user1{\mathcal{B}}}{\left( {\delta \eta } \right)}{\left( \tau \right)}} \\ { = {\user1{\mathcal{B}}}{\left( {A{\left( {\eta _{0} + \delta \eta {\left( t \right)}} \right)}} \right)}} \\ { = A{\user1{\mathcal{B}}}{\left( {\eta _{0} } \right)} + A{\user1{\mathcal{B}}}{\left( {\delta \eta } \right)}{\left( \tau \right)}} \\ \end{array} $$

(A‐12)

which can be rewritten (because ${\user1{\mathcal{B}}}{\left( k \right)} = k$) as:

$${\user1{\mathcal{B}}}{\left( {\delta \eta } \right)}{\left( \tau \right)} = {\left( {1 - \tau A} \right)}^{{ - 1}} A\eta _{0} \tau $$

(A‐13)

Equation (A-11) and (A-13) show that the Crank–Nicolson integration of a linear system is equivalent to the Borel transform of the system through the relationship:

$$\widehat{\delta }\eta {\left( t \right)} = 2{\user1{\mathcal{B}}}{\left( {\delta \eta } \right)}{\left( {\frac{t}{2}} \right)}$$

(A‐14)

Time evolution of the model

For each time step, the ZOOM solver solves the second matrix equation of (A-7) for ${\user1{\mathcal{B}}}{\left[ {{\mathop \delta \limits^o }\varphi } \right]}$. The first equation isthen solved for ${\user1{\mathcal{B}}}{\left[ {{\mathop \delta \limits^o }\eta } \right]}$. Thanks to property (A-14), this gives an approximation of the temporal evolution of the model variables between t _n and t _n + δt.

TLS Analysis

As is well known, poles of Laplace transform of TLS solutions are eigenmodes of the system. The same holds for Borel transform: determining the poles of the Borel transform yields the complete dynamic of the system.

ZOOM is able of computing numerically the Borel transform of the TLS solution ${\left( {{\user1{\mathcal{B}}}{\left[ {{\mathop \delta \limits^ \circ }\eta } \right]}{\left( \tau \right)}{\text{ and }}{\user1{\mathcal{B}}}{\left[ {{\mathop \delta \limits^ \circ }\varphi } \right]}{\left( \tau \right)}} \right)}$ on the real axis τ > 0. The problem of describing the dynamics of a system is thus reduced to that of determining the poles of the Borel transform of the TLS solution from its numerical values on the positive real axis.

In particular, in equation (A-7), the poles of ${\user1{\mathcal{B}}}{\left[ {{\mathop \delta \limits^o }\varphi } \right]}{\left( \tau \right)}$ are 1) the poles of ${\user1{\mathcal{B}}}{\left[ {{\mathop \delta \limits^ \circ }\varphi _{{{\text{ins}}}} } \right]}$, i.e., the poles of the model without taking into account the interactions between subsystems and 2) the poles of ${\left( {1 + \underline{\underline {\user1{\mathcal{C}}}} } \right)}^{{ - 1}}$, i.e. the poles corresponding to the subsystem interaction. The inverse Borel transform of equation (A-7), obtained by an identification of simple elements, provides the full dynamics of the model. The methodology consists here in fitting the Borel transform with a linear combination of sigmoid and bump functions, which are the only possible Borel transforms of linear differential equation solutions. From the characteristic times of the corresponding poles and their residue, the original function can easily be reconstructed without inverse Borel transform.