Interaction of magnetoelastic shear waves with a Griffith crack in an infinite strip

Abstract

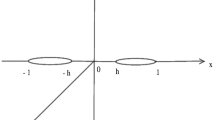
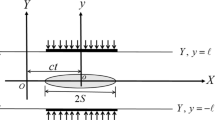
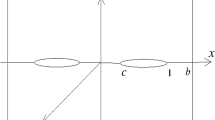
In this research paper, the diffraction of a Griffith crack, situated in an infinite strip of finite thickness, due to magnetoelastic shear wave propagation has been analyzed. The effect of magnetic field on the Griffith crack interaction has been studied. Fourier transform is used to reduce the mixed boundary value problem to the dual integral equations. Finally, with the help of Abel’s transform the integral equations have been converted to Fredholm integral equation of 2nd kind. Fox and Goodwin method is used to solve the integral equation numerically. The analytical expression of Stress Intensity Factor at the crack tip has been illustrated graphically for the cases with magnetic effect and without magnetic effect.

Appendix

Using common finite-difference integration formulae, we can write the following integral as

$$\begin{aligned} \frac{1}{h}\int _{0}^{0+nh}g(t)\mathrm{{d}}t=\frac{1}{2}g_0+g_1 +\cdots +g_{n-1}+\frac{1}{2}g_n+\Delta , \end{aligned}$$

(46)

where $g_0=g(0),\;g_r=g(0+rh),\;g_n=g(0+nh)=g(1)$ and $\Delta ,$ the difference correction, is a function of the differences of g.

The expression of $\Delta$ (Using Newton’s Forward Difference) is

$$\begin{aligned} \Delta =\left( -\frac{1}{12}\Delta ^1+\frac{1}{24} \Delta ^2-\frac{19}{720}\Delta ^3\cdots \right) \left( g_n-g_0\right) . \end{aligned}$$

Equation (41) can be written as

$$\begin{aligned} \int _{0}^{1}g(u)K(u,t)\mathrm{{d}}u=1-g(t) \end{aligned}$$

(47)

where $K(u,t)=uL(u,t).$ Using Eq. (46) for the representation of the integral, we can write Eq. (47) in the form

$$\begin{aligned} h\left[ \frac{1}{2}K(0,t)g_0+K(1,t)g_1+\cdots +K(n-1,t) g_{n-1}+\frac{1}{2}K(n,t)g_n+\Delta (t)\right] =1-g(t), \end{aligned}$$

where K(s, t) denotes the values of K(u, t) at the point (sh, t) . In this equation, we can put any value of t within (0, 1) for which K is defined, but the same $(n+1)$ values of g, at the equidistant pivotal points in the range (0, 1) have been considered for t. Since g(t) also seems on the right, however, it is preferable to set the $t'$s to be pivotal points of (0, 1) . Taking all pivotal points into consideration we can replace the integral equation by a set of $(n+1)$ linear simultaneous equations represented by

$$\begin{aligned} h\left[ \frac{1}{2}K(0,r)g_0+K(1,r)g_1+\cdots +K(n-1,r)g_{n-1}+\frac{1}{2}K(n,r)g_n+\Delta _r\right] =1-g_r, \end{aligned}$$

(48)

where, K(s, r) denotes the values of K(u, t) at the point (sh, rh) and r takes the values $0,\;1,\;2,\cdots ,n.$ Merging the $g_r$ on the left with those on the right, we can write Eq. (48) in the following form

$$\begin{aligned} \begin{aligned}&\left( 1+\frac{1}{2}hK(0,0)\right) g_0+hK(1,0)g_1+\cdots +hK(n-1,0)g_{n-1}+\frac{1}{2}hK(n,0)g_n=1-h\Delta _0,\\&\frac{1}{2}hK(0,1)g_0+\left( 1+hK(1,1)\right) g_1+\cdots +hK(n-1,1)g_{n-1}+\frac{1}{2}hK(n,1)g_n=1-h\Delta _1,\\&\vdots \\&\frac{1}{2}hK(0,n-1)g_0+hK(1,n-1)g_1+\cdots +\left( 1+hK(n-1,n-1)\right) g_{n-1}+\frac{1}{2}hK(n,n-1)g_n=1-h\Delta _{n-1}\\&\frac{1}{2}hK(0,n)g_0+hK(1,n)g_1+\cdots +hK(n-1,n)+\left( 1+\frac{1}{2}hK(n,n)\right) g_n=1-h\Delta _n. \end{aligned} \end{aligned}$$

(49)

We obtained the approximate value of $g_r\;(r=0,\;1,\;\ldots ,n)$ from Eq. (49), in which all the $\Delta _r$ have been calculated and inserted as corrections to the right-hand side of Eq. (49).