Skip to main content
SpringerLink
Log in

Transport of a reactive solute in a pulsatile non-Newtonian liquid flowing through an annular pipe

  • Published:
Journal of Engineering Mathematics Aims and scope Submit manuscript

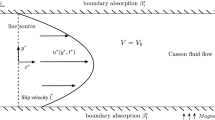
Abstract

The impact of heterogeneous (kinetic reversible phase exchange and irreversible absorption) chemical reactions along with a homogeneous first-order reaction is considered for the dispersion of a solute in a solvent flowing through an annular pipe under a periodic pressure gradient. A Casson model is used to describe the non-Newtonian viscosity of the liquid. The Aris–Barton method of moments is employed to study the behavior of the dispersion coefficient. The axial distribution of the mean concentration is determined using the Hermite polynomial representation of central moments. This study focuses on the transport phenomena in terms of the dispersion coefficient due to multiple kinds of reaction, yield stress, radius ratio, etc., which could be useful for analysis of flow of physiological blood-like liquids.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  1. Taylor GI (1953) Dispersion of soluble matter in solvent flowing slowly through a tube. Proc R Soc Lond A 219(1137):186–203

    Article  Google Scholar 

  2. Aris R (1956) On the dispersion of a solute in a fluid flowing through a tube. Proc R Soc Lond A 235(1200):67–77

    Article  Google Scholar 

  3. Ananthakrishnan V, Gill WN, Barduhn AJ (1965) Laminar dispersion in capillaries: Part I. Mathematical analysis. AlChE J 11(6):1063–1072

    Article  Google Scholar 

  4. Gill WN, Sankarasubramanian R (1970) Exact analysis of unsteady convective diffusion. Proc R Soc Lond A 316(1526):341–350

    Article  MATH  Google Scholar 

  5. Barton NG (1983) On the method of moments for solute dispersion. J Fluid Mech 126:205–218

    Article  MATH  Google Scholar 

  6. Aris R (1960) On the dispersion of a solute in pulsating flow through a tube. Proc R Soc Lond A 259(1298):370–376

    Article  MathSciNet  MATH  Google Scholar 

  7. Watson EJ (1983) Diffusion in oscillatory pipe flow. J Fluid Mech 133:233–244

    Article  MathSciNet  MATH  Google Scholar 

  8. Mazumder BS, Das SK (1992) Effect of boundary reaction on solute dispersion in pulsatile flow through a tube. J Fluid Mech 239:523–549

    Article  Google Scholar 

  9. Mukherjee A, Mazumder BS (1988) Dispersion of contaminant in oscillatory flows. Acta Mech 74(1–4):107–122

    Article  MathSciNet  MATH  Google Scholar 

  10. Roy AK, Saha AK, Debnath S (2017) On dispersion in oscillatory annular flow driven jointly by pressure pulsation and wall oscillation. J Appl Fluid Mech 10(5):1487–1500

    Article  Google Scholar 

  11. Chatwin PC (1975) On the longitudinal dispersion of passive contaminant in oscillatory flows in tubes. J Fluid Mech 71(3):513–527

    Article  MATH  Google Scholar 

  12. Bandyopadhyay S, Mazumder BS (1999) Unsteady convective diffusion in a pulsatile flow through a channel. Acta Mech 134(1–2):1–16

    Article  MathSciNet  MATH  Google Scholar 

  13. Barik S, Dalal DC (2017) On transport coefficients in an oscillatory Couette flow with nonlinear chemical decay reactions. Acta Mech 228(7):2391–2412

    Article  MathSciNet  MATH  Google Scholar 

  14. Sarkar A, Jayaraman G (2004) The effect of wall absorption on dispersion in oscillatory flow in an annulus: application to a catheterized artery. Acta Mech 172(3–4):151–167

    Article  MATH  Google Scholar 

  15. Mazumder BS, Mondal KK (2005) On solute transport in oscillatory flow through an annular pipe with a reactive wall and its application to a catheterized artery. Q J Mech Appl Math 58(3):349–365

    Article  MathSciNet  MATH  Google Scholar 

  16. Pedley TJ, Kamm RD (1988) The effect of secondary motion on axial transport in oscillatory tube flow. J Fluid Mech 193:347–367

    Article  MATH  Google Scholar 

  17. Jayaraman G, Pedley TJ, Goyal A (1998) Dispersion of solute in a fluid flowing through a curved tube with absorbing walls. Q J Mech Appl Math 51(4):577–598

    Article  MATH  Google Scholar 

  18. Mazumder BS, Bandyopadhyay S (2001) On solute dispersion from an elevated line source in an open-channel flow. J Eng Math 40(2):197–209

    Article  MATH  Google Scholar 

  19. Al Mukahal FHH, Duffy BR, Wilson SK (2017) Advection and Taylor–Aris dispersion in rivulet flow. Proc R Soc Lond A 473(2207):20170524

    Article  MathSciNet  MATH  Google Scholar 

  20. Agrawal S, Jayaraman G (1994) Numerical simulation of dispersion in the flow of power law fluids in curved tubes. Appl Math Model 18(9):504–512

    Article  MATH  Google Scholar 

  21. Siddheshwar PG, Manjunath S, Markande S (2000) Effect of interphase mass transfer on unsteady convective diffusion: Part I, plane-Poiseuille flow of a power-law fluid in a channel. Chem Eng Commun 180(1):187–207

    Article  Google Scholar 

  22. Siddheshwar PG, Markande S, Manjunath S (2000) Effect of interphase mass transfer on unsteady convective diffusion: Part II, Hagen Poiseuille flow of a power law fluid in a tube. Chem Eng Commun 180(1):209–229

    Article  Google Scholar 

  23. Sharp MK (1993) Shear-augmented dispersion in non-Newtonian fluids. Ann Biomed Eng 21(4):407–415

    Article  Google Scholar 

  24. Tu C, Deville M (1996) Pulsatile flow of non-Newtonian fluids through arterial stenoses. J Biomech 29(7):899–908

    Article  Google Scholar 

  25. Long Q, Xu XY, Ramnarine KV, Hoskins P (2001) Numerical investigation of physiologically realistic pulsatile flow through arterial stenosis. J Biomech 34(10):1229–1242

    Article  Google Scholar 

  26. Blair GS (1959) An equation for the flow of blood, plasma and serum through glass capillaries. Nature 183(4661):613–614

    Article  Google Scholar 

  27. Charm S, Kurland G (1965) Viscometry of human blood for shear rates of 0–100,000 \(\text{ sec }^{-1}\). Nature 206(4984):617–618

    Article  Google Scholar 

  28. Dash RK, Jayaraman G, Mehta KN (2000) Shear augmented dispersion of a solute in a Casson fluid flowing in a conduit. Ann Biomed Eng 28(4):373–385

    Article  Google Scholar 

  29. Nagarani P, Sarojamma G, Jayaraman G (2004) Effect of boundary absorption in dispersion in Casson fluid flow in a tube. Ann Biomed Eng 32(5):706–719

    Article  MATH  Google Scholar 

  30. Sankar DS (2009) A two-fluid model for pulsatile flow in catheterized blood vessels. Int J Nonlinear Mech 44(4):337–351

    Article  MATH  Google Scholar 

  31. Roy AK, Saha AK, Debnath S (2018) Unsteady convective diffusion with interphase mass transfer in Casson liquid. Periodica Polytech Chem Eng 62(2):215–223

    Article  Google Scholar 

  32. Nagarani P, Sarojamma G, Jayaraman G (2006) Exact analysis of unsteady convective diffusion in Casson fluid flow in an annulus—application to catheterized artery. Acta Mech 187(1–4):189–202

    Article  MATH  Google Scholar 

  33. Rana J, Murthy PVSN (2016) Solute dispersion in pulsatile Casson fluid flow in a tube with wall absorption. J Fluid Mech 793:877–914

    Article  MathSciNet  MATH  Google Scholar 

  34. Debnath S, Saha AK, Mazumder BS, Roy AK (2017) Hydrodynamic dispersion of reactive solute in a Hagen–Poiseuille flow of a layered liquid. Chin J Chem Eng 25(7):862–873

    Article  Google Scholar 

  35. Debnath S, Saha AK, Mazumder BS, Roy AK (2017) Dispersion phenomena of reactive solute in a pulsatile flow of three-layer liquids. Phys Fluids 29(9):097107

    Article  Google Scholar 

  36. Alper E (1983) Mass transfer with chemical reaction in multiphase systems: volume I: two-phase systems. Volume II: three-phase systems. Springer, Dordrecht

  37. Kinne FL (1972) Mass transfer in the human respiratory system. Digital Repository. Iowa State University

  38. El-Sayed MF, Eldabe NTM, Ghaly AY, Sayed HM (2011) Effects of chemical reaction, heat, and mass transfer on non-Newtonian fluid flow through porous medium in a vertical peristaltic tube. Transp Porous Media 89(2):185–212

    Article  MathSciNet  Google Scholar 

  39. Walker RE (1961) Chemical reaction and diffusion in a catalytic tubular reactor. Phys Fluids 4(10):1211–1216

    Article  Google Scholar 

  40. Gupta PS, Gupta AS (1972) Effect of homogeneous and heterogeneous reactions on the dispersion of a solute in the laminar flow between two plates. Proc R Soc Lond A 330(1580):59–63

    Article  MATH  Google Scholar 

  41. Purnama A (1988) Boundary retention effects upon contaminant dispersion in parallel flows. J Fluid Mech 195:393–412

    Article  MathSciNet  MATH  Google Scholar 

  42. Ng CO, Rudraiah N (2008) Convective diffusion in steady flow through a tube with a retentive and absorptive wall. Phys Fluids 20(7):073604

    Article  MATH  Google Scholar 

  43. Ng CO (2006) Dispersion in open-channel flow subject to the processes of sorptive exchange on the bottom and air–water exchange on the free surface. Fluid Dyn Res 38(6):359–385

    Article  MathSciNet  MATH  Google Scholar 

  44. Ng CO (2006) Dispersion in steady and oscillatory flows through a tube with reversible and irreversible wall reactions. Proc R Soc Lond A 462(2066):481–515

    Article  MathSciNet  MATH  Google Scholar 

  45. Mazumder BS, Paul S (2012) Dispersion of reactive species with reversible and irreversible wall reactions. Heat Mass Transf 48(6):933–944

    Article  Google Scholar 

  46. Debnath S, Paul S, Roy AK (2018) Transport of reactive species in oscillatory annular flow. J Appl Fluid Mech 11(2):405–417

    Article  Google Scholar 

  47. McDonald DA (1974) Blood flow in arteries. Edward Arnold, London

    Google Scholar 

  48. Nagarani P, Sebastian BT (2013) Dispersion of a solute in pulsatile non-Newtonian fluid flow through a tube. Acta Mech 224(3):571–585

    Article  MathSciNet  MATH  Google Scholar 

  49. Fung YC (1993) Biomechanics: mechanical properties of living tissues. Springer, New York

    Book  Google Scholar 

  50. Aroesty J, Gross JF (1972) The mathematics of pulsatile flow in small blood vessels: I. Casson Theory. Microvasc Res 4(1):1–12

    Article  Google Scholar 

  51. Schwarzenbach RP, Gschwend PM, Imboden DM (1993) Environmental organic chemistry. Wiley, New York

    Google Scholar 

  52. Sankar DS, Lee U (2009) Two-fluid non-Newtonian models for blood flow in catheterized arteries—a comparative study. J Mech Sci Technol 23(9):2444–2455

    Article  Google Scholar 

  53. Anderson D, Tannehill JC, Pletcher RH (1984) Computational fluid mechanics and heat transfer. Hemisphere Publishing Corporation, New York

    MATH  Google Scholar 

  54. Lau MW, Ng CO (2007) On the early development of dispersion in flow through a tube with wall reactions. In: New trends in fluid mechanics research. Springer, Berlin, pp 670–673

  55. Phillips CG, Kaye SR, Robinson CD (1995) Time-dependent transport by convection and diffusion with exchange between two phases. J Fluid Mech 297:373–401

    Article  MathSciNet  MATH  Google Scholar 

  56. Shaul S, Kalman H (2015) Three plugs model. Powder Technol 283:579–592

    Article  Google Scholar 

  57. Merrill EW (1969) Rheology of blood. Physiol Rev 49(4):863–888

    Article  Google Scholar 

  58. Merrill EW, Benis AM, Gilliland ER, Sherwood TK, Salzman EW (1965) Pressure-flow relations of human blood in hollow fibers at low flow rates. J Appl Physiol 20(5):954–967

    Article  Google Scholar 

  59. Levenspiel O, Smith WK (1957) Notes on the diffusion-type model for the longitudinal mixing of fluids in flow. Chem Eng Sci 6(4–5):227–235

    Article  Google Scholar 

  60. Mehta RV, Merson RL, McCoy BJ (1974) Hermite polynomial representation of chromatography elution curves. J Chromatogr A 88(1):1–6

    Article  Google Scholar 

  61. Wang P, Chen GQ (2016) Transverse concentration distribution in Taylor dispersion: Gill’s method of series expansion supported by concentration moments. Int J Heat Mass Transf 95:131–141

    Article  Google Scholar 

Download references

Acknowledgements

The authors are grateful to the editor and reviewers for constructive comments and suggestions that helped to improve this article. S.D. is grateful to the National Institute of Technology, Agartala, India for financial support to pursue this work.

Author information

Author notes

  1. B. S. Mazumder

    Present address: Department of Civil Engineering, Indian Institute of Technology Bombay, Mumbai, 400076, India

Authors and Affiliations

  1. Department of Mathematics, National Institute of Technology, Agartala, 799046, India

    Sudip Debnath, Apu Kumar Saha & Ashis Kumar Roy

  2. Fluvial Mechanics Laboratory, Physics and Applied Mathematics Unit, Indian Statistical Institute, Kolkata, 700108, India

    B. S. Mazumder

  3. Department of Aerospace Engineering and Applied Mechanics, Indian Institute of Engineering Science and Technology, Shibpur, Howrah, 711103, India

    B. S. Mazumder

Authors
  1. Sudip Debnath
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Apu Kumar Saha
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. B. S. Mazumder
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Ashis Kumar Roy
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sudip Debnath.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

The first correction of the shear stress (\(\tau _1\)) is derived as follows:

Since

$$\begin{aligned} \frac{\partial {u_0}}{\partial {t}}=\frac{\partial {u_0}}{\partial {p}}\frac{\mathrm {d}p}{\mathrm {d}t}+\frac{\partial {u_0}}{\partial {\lambda }}\frac{\mathrm {d} \lambda }{\mathrm {d}t}, \end{aligned}$$

Eq. (35) can be written as

$$\begin{aligned} \tau _1= & {} \frac{1}{r}\int _{r}^{\lambda }\left( \frac{\partial {u_0}}{\partial {p}}\frac{\mathrm {d}p}{\mathrm {d}t}+\frac{\partial {u_0}}{\partial {\lambda }}\frac{\mathrm {d} \lambda }{\mathrm {d}t}\right) r\, \mathrm {d}r+\frac{D_1(t)}{r}\\= & {} \frac{1}{r}\left[ \frac{\mathrm {d}p}{\mathrm {d}t}\int _{r}^{\lambda }\frac{\partial {u_0}}{\partial {p}}r \mathrm {d}r+\frac{\mathrm {d}\lambda }{\mathrm {d}t}\int _{r}^{\lambda } \frac{\partial {u_0}}{\partial {\lambda }} r \mathrm {d}r\right] +\frac{D_1(t)}{r}. \end{aligned}$$

Explicitly,

$$\begin{aligned} \tau _1= & {} \frac{1}{r}\left[ \frac{\mathrm {d}p}{\mathrm {d}t}\int _{r}^{\lambda _1} \frac{\partial {u_0^+}}{\partial {p}} r \mathrm {d}r+\frac{\mathrm {d} \lambda }{\mathrm {d}t} \int _{r}^{\lambda _1}\frac{\partial {u_0^+}}{\partial {\lambda }}r \mathrm {d}r\right] \nonumber \\&\quad +\left( \frac{ \lambda ^2-\lambda _1^2}{2r}\right) \left[ \frac{\mathrm {d}p}{\mathrm {d}t} \frac{\partial {u_{0\mathrm{p}}^-}}{\partial {p}}+\frac{\mathrm {d} \lambda }{\mathrm {d}t}\frac{\partial {u_{0\mathrm{p}}^-}}{\partial {\lambda }} \right] +\frac{D_1(t)}{r}\quad \text{ if } \; r_\mathrm {i}\le r\le \lambda _1, \end{aligned}$$
(A.1a)
$$\begin{aligned} \tau _1= & {} \left( \frac{\lambda ^2-r^2}{2r}\right) \left[ \frac{\mathrm {d}p}{\mathrm {d}t} \frac{\partial {u_{0\mathrm{p}}^-}}{\partial {p}}+\frac{\mathrm {d} \lambda }{\mathrm {d}t}\frac{\partial {u_{0\mathrm{p}}^-}}{\partial {\lambda }} \right] +\frac{D_1(t)}{r} \quad \text{ if } \; \lambda _1\le r\le \lambda _2, \end{aligned}$$
(A.1b)
$$\begin{aligned} \tau _1= & {} \left( \frac{\lambda ^2-\lambda _2^2}{2r}\right) \left[ \frac{\mathrm {d}p}{\mathrm {d}t} \frac{\partial {u_{0\mathrm{p}}^-}}{\partial {p}}+\frac{\mathrm {d} \lambda }{\mathrm {d}t}\frac{\partial {u_{0\mathrm{p}}^-}}{\partial {\lambda }} \right] +\frac{D_1(t)}{r} \nonumber \\&\quad -\frac{1}{r}\left[ \frac{\mathrm {d}p}{\mathrm {d}t}\int _{\lambda _2}^{r}\frac{\partial {u_0^{++}}}{\partial {p}} r \mathrm {d}r+\frac{\mathrm {d}\lambda }{\mathrm {d}t}\int _{\lambda _2}^{r}\frac{\partial {u_0^{++}}}{\partial {\lambda }} r \mathrm {d}r\right] \quad \text{ if } \; \lambda _2\le r\le r_\mathrm {o}. \end{aligned}$$
(A.1c)

Now, using the values of

$$\begin{aligned} \frac{\partial {u_0^+}}{\partial {p}} ,\frac{\partial {u_0^+}}{\partial {\lambda }}, \frac{\partial {u_{0\mathrm{p}}^-}}{\partial {p}}, \frac{\partial {u_{0\mathrm{p}}^-}}{\partial {\lambda }},\frac{\partial {u_0^{++}}}{\partial {p}} ,\frac{\partial {u_0^{++}}}{\partial {\lambda }}, \end{aligned}$$

Equations (A.1a)–(A.2c) can be rewritten as

$$\begin{aligned} \tau _1= & {} \frac{1}{4r}\frac{\mathrm {d}p}{\mathrm {d}t}\left[ 2\lambda ^2\left\{ 2\left( \lambda _1^2 \log (\lambda _1)-r^2 \log (r)\right) -\left( \lambda _1^2 -r^2\right) \left( 1+2 \log (r_\mathrm {i})\right) \right\} +\left( \lambda _1^2-r^2\right) \left( 2 r_\mathrm {i}^2-\lambda _1^2-r^2\right) \right. \nonumber \\&\quad +2\left( \lambda ^2-\lambda _1^2\right) \left\{ 2\lambda ^2 \log \left( \frac{\lambda _1}{r_\mathrm {i}}\right) -\left( \lambda _1^2- r_\mathrm {i}^2\right) \right\} -2(2\varLambda )^\frac{1}{2}\left\{ 2\int _{r}^{\lambda _1}\left( \int _{r_\mathrm {i}}^{r} \left( \frac{\lambda ^2-r^2}{r}\right) ^{\frac{1}{2}} \mathrm {d}r\right) r \,\mathrm {d}r \right. \nonumber \\&\quad \left. \left. +\left( \lambda ^2-\lambda _1^2\right) \int _{r_\mathrm {i}}^{\lambda _1}\left( \frac{\lambda ^2- r^2}{r}\right) ^\frac{1}{2} \mathrm {d}r\right\} \right] + \frac{p(t)\lambda }{r} \frac{\mathrm {d}\lambda }{\mathrm {d}t}\left[ 2\left( \lambda _1^2 \log (\lambda _1)-r^2 \log (r)\right) \right. \nonumber \\&\quad -\left( \lambda _1^2-r^2\right) \left( 1+2 \log (r_\mathrm {i})\right) +2\left( \lambda ^2-\lambda _1^2\right) \log \left( \frac{\lambda _1}{r_\mathrm {i}}\right) \nonumber \\&\left. \quad -(2\varLambda )^\frac{1}{2}\left\{ 2 \int _{r}^{\lambda _1}\left( \int _{r_\mathrm {i}}^{r} \frac{1}{ \sqrt{r(\lambda ^2-r^2)}} \mathrm {d}r \right) r\, \mathrm {d}r +\left( \lambda ^2-\lambda _1^2\right) \int _{r_\mathrm {i}}^{\lambda _1} \frac{1}{\sqrt{r(\lambda ^2-r^2)}} \mathrm {d}r\right\} \right] \nonumber \\&\quad +\frac{D_1(t)}{r} \quad \text{ if } \; r_\mathrm {i}\le r\le \lambda _1,\end{aligned}$$
(A.2a)
$$\begin{aligned} \tau _1= & {} \left( \frac{\lambda ^2- r^2}{2 r}\right) \frac{\mathrm {d}p}{\mathrm {d}t}\left[ 2\lambda ^2 \log \left( \frac{\lambda _1}{r_\mathrm {i}}\right) -\left( \lambda _1^2-r_\mathrm {i}^2\right) \right. \left. -(2\varLambda )^\frac{1}{2} \int _{r_\mathrm {i}}^{\lambda _1}\left( \frac{\lambda ^2-r^2}{r}\right) ^\frac{1}{2} \mathrm {d}r\right] \nonumber \\&\quad +\left( \frac{\lambda ^2- r^2}{ r}\right) \frac{\mathrm {d}\lambda }{\mathrm {d}t} p(t) \lambda \left[ 2 \log \left( \frac{\lambda _1}{r_\mathrm {i}}\right) \right. \left. -(2\varLambda )^\frac{1}{2}\int _{r_\mathrm {i}}^{\lambda _1} \frac{1}{\sqrt{r(\lambda ^2-r^2)}}\mathrm {d}r\right] +\frac{D_1(t)}{r}\quad \text{ if } \; \lambda _1\le r\le \lambda _2, \end{aligned}$$
(A.2b)
$$\begin{aligned} \tau _1= & {} \frac{1}{4r}\frac{\mathrm {d}p}{\mathrm {d}t}\left[ 2\lambda ^2\left\{ \left( r^2-\lambda _2^2\right) \left( 1+2 \log (r_\mathrm {o})\right) -2\left( r^2 \log (r)\right. \right. \right. \left. \left. \left. -\lambda _2^2 \log (\lambda _2)\right) \right\} +\left( r^2-\lambda _2^2\right) \left( r^2+\lambda _2^2-2 r_\mathrm {o}^2\right) \right. \nonumber \\&\quad +\left. 2\left( \lambda _2^2-\lambda ^2\right) \left\{ \lambda _1^2-r_\mathrm {i}^2-2\lambda ^2 \log \left( \frac{\lambda _1}{r_\mathrm {i}}\right) \right\} \right. \left. +\, 2(2\varLambda )^\frac{1}{2}\left\{ \int _{\lambda _2}^{r} 2\left( \int _{r}^{r_\mathrm {o}}\left( \frac{r^2-\lambda ^2}{r}\right) ^\frac{1}{2} \mathrm {d}r\right) r\, \mathrm {d}r \right. \right. \nonumber \\&\quad +\left( \lambda _2^2-\lambda ^2\right) \left. \left. \int _{r_\mathrm {i}}^{\lambda _1}\left( \frac{\lambda ^2-r^2}{r}\right) ^\frac{1}{2} \mathrm {d}r\right\} \right] +\frac{p(t)}{r} \lambda \frac{\mathrm {d}\lambda }{\mathrm {d}t}\left[ \left( r^2-\lambda _2^2\right) \left( 1+2 \log (r_\mathrm {o})\right) \right. \left. \right. \nonumber \\&\quad -2\left( r^2 \log (r)-\lambda _2^2 \log (\lambda _2)\right) -2\left( \lambda _2^2-\lambda ^2\right) \log \left( \frac{\lambda _1}{r_\mathrm {i}}\right) \nonumber \\&\left. \quad -(2\varLambda )^\frac{1}{2} \left\{ 2\int _{\lambda _2}^{r}\left( \int _{r}^{r_\mathrm {o}} \frac{1}{\sqrt{r(r^2-\lambda ^2)}}\mathrm {d}r\right) r \,\mathrm {d}r -\left( \lambda _2^2-\lambda ^2\right) \int _{r_\mathrm {i}}^{\lambda _1} \frac{1}{\sqrt{r(\lambda ^2-r^2)}} \mathrm {d}r \right\} \right] \nonumber \\&\quad +\frac{D_1(t)}{r} \quad \text{ if } \; \lambda _2\le r\le r_\mathrm {o}. \end{aligned}$$
(A.2c)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Debnath, S., Saha, A.K., Mazumder, B.S. et al. Transport of a reactive solute in a pulsatile non-Newtonian liquid flowing through an annular pipe. J Eng Math 116, 1–22 (2019). https://doi.org/10.1007/s10665-019-09999-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10665-019-09999-1

Keywords

Search

Navigation