1 Introduction

The concept of fractional-order differentiation and integration is not new in mathematics. Its history is quite long and was initiated at least in the late seventeenth century. According to the research conducted in [1], de l’Hospital and Leibnitz considered differential operators with non-integral order in their correspondence dated 30 September 1695. The nineteenth century was a period of intense prosperity for the theory of fractional derivatives. The series of papers (1832–1892) published by Liouville and Riemann gave a solid foundation in fractional calculus. Over the next century, many mathematicians, physicists and engineers, motivated by the needs of industrial problems, were developing the theory of fractional derivatives in the context of their applications. It has been proven immediately that the fractional derivative is a significant tool applicable in many areas including diffusive transport, fluid flow and especially in rheology, where fractional derivative models are effective to describe the dynamic behaviour of real viscoelastic materials [2,3,4,5,6,7,8,9,10,11].

The theory of viscoelasticity is crucial in describing materials, such as rubber or polymers, which exhibit time-dependent stress–strain behaviour. In many industry applications, like tyres, shock absorbers or other rubber components, a reliable constitutive equation must be established in order to describe all the relevant effects in the material response under small harmonic vibrations. The classical model of finite viscoelasticity is based on a finite series of Maxwell elements in parallel, which leads to a relaxation function given by a sum of decreasing exponentials (Prony series) (see [12]). Experimental investigations into the time-dependent relaxation behaviour of such materials are characterised by a very fast decrease of the stress at the beginning of the relaxation process and an extremely slow decay for large times. It can even take a long time before a constant asymptotic value is reached. Therefore, a lot of Maxwell elements are required to describe relaxation behaviour with sufficient accuracy. This ends in a difficult optimisation problem in order to identify a large number of material parameters. On the other hand, over the years, the concept of fractional derivatives has been introduced to the theory of viscoelasticity [13,14,15,16]. Among these models, the fractional Zener model was found to be very effective to predict the dynamic nature of rubber-like materials with only a small number of material parameters [17,18,19,20]. The solution of the corresponding constitutive equation leads to a relaxation function of the Mittag-Leffler type. It is defined by the power series with negative arguments. This function represents all essential properties of relaxation process under the influence of an arbitrary and continuous signal with a jump at the origin. However, from the numerical point of view, it is inconvenient to calculate the numerical values of the Mittag-Leffler function for large negative arguments. Our motivation is to discuss and solve this computational difficulty against a background of physical and application interest.

The paper is organized in the following way. In the first part (Sect. 2), we recall the main properties of the Mittag-Leffler function and introduce the linear operators of fractional differentiation. In the second part (Sect. 3), we consider differential equation of fractional order, which model the constitutive relation for viscoelastic materials. For this equation, we derive its analytical solution by applying the technique of Laplace transforms. It is given in the terms of the Mittag-Leffler function. We present the method of calculating numerical values of Mittag-Leffler function for arbitrary negative arguments, which is based on its integral representation. Finally, a numerical simulation is given to illustrate the effectiveness of the proposed approach. Section 4 contains some concluding remarks.

2 Preliminaries and notations

We start our considerations by introducing several special functions, fractional operators and their properties that will be useful in the second part of this work. Some definitions in this section are very common, and we write them just for reference. Others are far from being common but are still quite often used in the literature [1, 21, 22].

2.1 Laplace transform

Definition 2.1

Let \(f:\mathbb {R}_+\rightarrow \mathbb {R}\) be a locally integrable function on the interval \([0,\infty )\) and s be a complex number. If the improper integral

$$\begin{aligned} \mathcal {L}[f(t)](s) := \int _0^{\infty }f(t)\mathrm {e}^{-st}\mathrm {d}t, \end{aligned}$$
(2.1)

exists, then we call it the Laplace transform of f at s.

Definition 2.2

Let \(f:\mathbb {R}_+\rightarrow \mathbb {R}\) be a real function and suppose that \(F(s) = \mathcal {L}[f(t)](s)\) is well defined for some \(s = \gamma +\mathrm {i} \theta \). Then, we have

$$\begin{aligned} f(t) = \frac{1}{2\pi \mathrm {i}}\int _{\gamma - \mathrm {i}\infty }^{\gamma + \mathrm {i}\infty }F(s)\mathrm {e}^{st}\mathrm {d}s, \end{aligned}$$
(2.2)

and it is called the inverse Laplace transform of F.

Property 2.1

Let f and g be any functions and \(c_1\) and \(c_2\) be any constants for which the needed operations are defined. Then, we can write the following properties of the Laplace transform

  1. (i)

    Linearity

    $$\begin{aligned} \mathcal {L}[(c_1 f+ c_2 g)(t)](s) = c_1\mathcal {L}[f(t)](s) + c_2\mathcal {L}[g(t)](s), \end{aligned}$$
  2. (ii)

    Differentiation

    $$\begin{aligned} \mathcal {L}\left[ \frac{\mathrm{{d}}}{\mathrm{{d}}t}f(t)\right] (s) = s\mathcal {L}[f(t)](s)-f(0), \end{aligned}$$
  3. (iii)

    Convolution

    $$\begin{aligned} \mathcal {L}[(f*g)(t)](s) = \mathcal {L}[f(t)](s)\mathcal {L}[g(t)](s). \end{aligned}$$

Here the convolution is defined by

$$\begin{aligned} f(t)*g(t)=\int _{0}^{t}f(t-\tau )g(\tau )\mathrm {d}\tau . \end{aligned}$$
(2.3)

2.2 Special functions

Definition 2.3

The Heaviside step function \(H:\mathbb {R}\rightarrow \mathbb {R}\) is a discontinuous function with discontinuity at zero, namely

$$\begin{aligned} H(t) = {\left\{ \begin{array}{ll} 0 &{} \text {if}\ t\le 0,\\ 1 &{} \text {if}\ t> 0. \end{array}\right. } \end{aligned}$$
(2.4)

The Heaviside step function may be defined equivalently as the integral of the Dirac delta function, that is

$$\begin{aligned} H(t) = \int _{-\infty }^{t}\delta (\tau )\mathrm {d}\tau . \end{aligned}$$
(2.5)

Definition 2.4

The Gamma function is defined by the integral

$$\begin{aligned} \varGamma (t) = \int ^{\infty }_{0}x^{t-1}\mathrm {e}^{-x}\mathrm {d}x. \end{aligned}$$
(2.6)

It can be proved by integrating by parts that the Gamma function satisfies the following functional equation

$$\begin{aligned} \varGamma (x+1)=x\varGamma (x), \end{aligned}$$
(2.7)

for arbitrary \(x>0\).

Definition 2.5

Let \(\alpha >0\) and \(\beta >0\) be two real but arbitrary numbers. The two-parameter Mittag-Leffler function \(E_{\alpha ,\beta }\) is defined by

$$\begin{aligned} E_{\alpha ,\beta }(t) = \sum _{k=0}^{\infty }\frac{t^k}{\varGamma (\alpha k + \beta )}, \end{aligned}$$
(2.8)

whenever the series converges.

Since

$$\begin{aligned} E_{1,1}(t) = \sum _{k=0}^{\infty }\frac{t^k}{\varGamma (k + 1)}=\sum _{k=0}^{\infty }\frac{t^k}{k!}=\mathrm {e}^t, \end{aligned}$$
(2.9)

is the well known exponential function, the Mittag-Leffler function is also known as the fractional exponential function.

Theorem 2.1

Let \(E_{\alpha ,\beta }\) be the two-parameter Mittag-Leffler function for some \(\alpha >0\) and \(\beta >0\). The power series defining \(E_{\alpha ,\beta }(t)\) is convergent for all \(t\in \mathbb {R}\).

Theorem 2.2

Let \(\alpha >0\), \(\beta >0\) and \(t\in \mathbb {R}\). Then

$$\begin{aligned} E_{\alpha ,\beta }(t)=t\,E_{\alpha ,\alpha +\beta }(t)+\frac{1}{\varGamma (\beta )}. \end{aligned}$$
(2.10)

Definition 2.6

Let \(\alpha >0\), \(\beta >0\) and \(a\in \mathbb {R}\). We define the function \(Z_{\alpha ,\beta }(\cdot \,;a)\) in the form

$$\begin{aligned} Z_{\alpha ,\beta }(t;a) = t^{\beta -1}E_{\alpha ,\beta }(at^{\alpha }). \end{aligned}$$
(2.11)

Lemma 2.1

The Laplace transform of \(Z_{\alpha ,\beta }(\cdot \,;a)\) is well defined and

$$\begin{aligned} \mathcal {L}[Z_{\alpha ,\beta }(t;a)](s) = \frac{s^{\alpha -\beta }}{s^{\alpha }-a}, \end{aligned}$$
(2.12)

for all complex numbers s satisfying the condition \(|a/s^{\alpha }|<1\).

2.3 Fractional derivatives

In the following subsection, we shall show the most popular definitions of the fractional-order derivative and describe their properties. We also present some similarities, differences and relations between them (see [1, 21, 22]). Let us start with the most popular definition of fractional derivative being a result of Liouville’s and Riemann’s work. It is based on a generalization of the Cauchy formula for n-fold integration. To be more precise, let f be a sufficiently regular function on the interval \([a,b]\subset \mathbb {R}\) and I denote the integral operator over [a, b]. The Cauchy integral formula is

$$\begin{aligned} I^nf(t) = \frac{1}{(n-1)!}\int _a^t(t-\tau )^{n-1}f(\tau )\mathrm {d}\tau , \end{aligned}$$
(2.13)

for \(t\in [a,b]\) and \(n\in \mathbb {N}\). Replacing the factorial operator with the Gamma function, being its natural generalization, Liouville and Riemann have created an integral operator in the following form

$$\begin{aligned} {_aI_t^{\alpha }f(t)} := \frac{1}{\varGamma (\alpha )}\int _a^t(t-\tau )^{\alpha -1}f(\tau )\mathrm {d}\tau , \end{aligned}$$
(2.14)

for any real number \(\alpha > 0\) and \(t\in [a,b]\).

Definition 2.7

Let \(f:[a,b]\rightarrow \mathbb {R}\) be an arbitrary function and \(\alpha \in (0,1)\). If the value

$$\begin{aligned} {_aD_t^{\alpha }f(t)} := \frac{\mathrm{{d}}}{\mathrm{{d}}t}{_aI_t^{1-\alpha }f(t)}, \end{aligned}$$
(2.15)

is finite, then we call it the Riemann–Liouville fractional derivative with order \(\alpha \) of function f.

In 1967, an Italian mathematician Michele Caputo [23] gave a different definition of fractional derivative, which has turned to be very useful in industrial problems.

Definition 2.8

Let \(\alpha \) be an arbitrary real number in the interval (0, 1) and \(f\in C^1([a,b])\). Then for every \(t\in [a,b]\) there exists a finite value

$$\begin{aligned} {_a^CD_t^{\alpha }f(t)} := \frac{1}{\varGamma (1-\alpha )}\int _a^t\frac{f'(\tau )}{(t-\tau )^{\alpha }}\mathrm {d}\tau , \end{aligned}$$
(2.16)

which is called the Caputo fractional derivative with order \(\alpha \) of function f.

Let us investigate some basic properties of these differential operators of fractional order. First of all, we notice that Definitions 2.7 and 2.8 are consistent with the classical integer order derivative, i.e.

$$\begin{aligned} \lim _{\alpha \rightarrow 1}{_a^CD_t^{\alpha }f(t)} = f'(t) = \lim _{\alpha \rightarrow 1}{_aD_t^{\alpha }f(t)}. \end{aligned}$$
(2.17)

Property 2.2

Let f, g be arbitrary functions and \(c_1\), \(c_2\), \(\alpha \), a be real constants for which the needed operations are defined. Then the linearity of the Riemann–Liouville and Caputo fractional derivatives can be expressed by

  1. 1.

    \(_a{D_t^{\alpha }(c_1 f+c_2 g)(t)} = c_1\, _a{D_t^{\alpha }f(t)} + c_2\, _a{D_t^{\alpha }g(t)}\),

  2. 2.

    \(_a^C{D_t^{\alpha }(c_1 f+c_2 g)(t)} = c_1\, _a^C{D_t^{\alpha }f(t)} + c_2\, _a^C{D_t^{\alpha }g(t)}\).

Property 2.3

Let f be a constant function, i.e. \(f(t)=c\), \(c\in \mathbb {R}\). Then, we have

$$\begin{aligned} {_aD_t^{\alpha }c} = \frac{c}{\varGamma (1-\alpha )(t-a)^{\alpha }} \ne 0,\ \ \alpha \in (0,1), \end{aligned}$$
(2.18)

and

$$\begin{aligned} {_a^CD_t^{\alpha }c} = 0,\ \ c\in \mathbb {R},\ \ \alpha \in (0,1), \end{aligned}$$
(2.19)

in the case of Riemann–Liouville and Caputo type, respectively.

Looking for the relationship between the Caputo and Riemann–Liouville fractional differential operators, we can present the following result.

Theorem 2.3

Let \(f:[a,b]\rightarrow \mathbb {R}\) be a differentiable function with order \(\alpha \in (0,1)\) in the sense of Definitions 2.7 and 2.8. Then

$$\begin{aligned} {_aD_t^{\alpha }f(t)} = {_a^CD_t^{\alpha }f(t)} + \frac{f(a)}{\varGamma (1-\alpha )(t-a)^{\alpha }}. \end{aligned}$$
(2.20)

Proposition 2.1

Let f be arbitrary functions and \(\alpha \) be a real constant for which the needed operations are defined. Then the Laplace transform of the Riemann–Liouville and Caputo fractional derivatives satisfy

  1. 1.

    \(\mathcal {L}[{_0D_t^{\alpha }f(t)}](s) = s^{\alpha }\mathcal {L}[f(t)](s) - \left[ {_0I_t^{1-\alpha }f(t)} \right| _{t=0}\),

  2. 2.

    \(\mathcal {L}[_0^C D_t^{\alpha }f(t)](s) = s^{\alpha }\mathcal {L}[f(t)](s) - s^{\alpha -1}f(0)\).

Practical applicability of the Laplace transform of the Riemann–Liouville fractional derivative is limited by the absence of the physical interpretation of the limit values of fractional derivative at \(t=0\). Since there is no such problem in the case of Caputo fractional derivative, it can be useful for solving applied problems leading to linear fractional differential equations.

3 Fractional viscoelastic constitutive model

In this section, we present the application of fractional derivatives in the constitutive model of viscoelasticity. To be more precise, we formulate the Caputo type fractional differential constitutive equation and solve it, applying the Laplace transformation technique for an arbitrary signal with a jump at \(t=0\). Furthermore, we discuss the inconvenience of numerical calculations of the relaxation function derived in terms of the Mittag-Leffler function.

3.1 Generalized Zener model of viscoelastic materials

The fractional Zener model is the generalization of the well-known standard linear solid model consisting of an ideal elastic spring and Maxwell element connected in parallel. The qualitative behaviour of the conventional model is improved by replacing the integer order time derivatives of stress and with fractional-order derivatives. The constitutive equation for the fractional Zener model is

$$\begin{aligned} \frac{\mathrm{d}^{\alpha }}{\mathrm{d}t^{\alpha }}\sigma (t) + A_0\sigma (t) = B_1\frac{\mathrm{d}^{\alpha }}{\mathrm{d}t^{\alpha }}\varepsilon (t) + B_0\varepsilon (t), \end{aligned}$$
(3.1)

where \(\sigma \) is the stress, \(\varepsilon \) is the, \(A_0,\, B_0,\, B_1\) and \(\alpha \in (0,1)\) are material constants,-order and the \(\alpha \)-th-order fractional derivative is defined by the Caputo operator (2.16). This model has been proved to be efficient in describing the stress–strain relation of real viscoelastic materials.

3.2 Analytical solution of the fractional-order differential constitutive equation

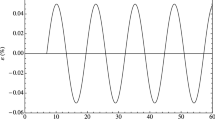
Let us consider the viscoelastic material subjected to an imposed arbitrary continuous deformation \(\varepsilon (t)\) with a jump at \(t=0\). We assume that the stress is zero before the is loaded, i.e. the material is in equilibrium. According to the Boltzmann superposition principle in viscoelasticity, we can express the signal as the sum of constant \(\varepsilon _1\) and continuous \(\varepsilon _2\) functions (see Fig.1). Then, we have

$$\begin{aligned} \varepsilon (t)=\varepsilon _1(t)+\varepsilon _2(t)=\varepsilon _0 H(t)+\varepsilon _2(t),\ \ \ t\ge 0, \end{aligned}$$
(3.2)

where H denotes the Heaviside step function. Linearity of the constitutive equation (3.1) and linearity of the Caputo fractional operator (Property 2.2) allows us to measure the corresponding stress response which can be expressed as

$$\begin{aligned} \sigma (t)=\sigma _1(t)+\sigma _2(t), \end{aligned}$$
(3.3)

where \(\sigma _1(t)\) and \(\sigma _2(t)\) are the stress histories corresponding to \(\varepsilon _1(t)\) and \(\varepsilon _2(t)\) seperately. Let us start with the equation

$$\begin{aligned} \frac{\mathrm{{d}}^{\alpha }}{\mathrm{{d}}t^{\alpha }}\sigma _1(t) + A_0\sigma _1(t) = B_1\frac{\mathrm{{d}}^{\alpha }}{\mathrm{{d}}t^{\alpha }}\varepsilon _1(t) + B_0\varepsilon _1(t). \end{aligned}$$
(3.4)

Inserting \(\varepsilon _1(t) = \varepsilon _0 H(t)\), applying the Laplace transform, using Property 2.1 and doing simple transformations, we get

$$\begin{aligned} \mathcal {L}[\sigma _1(t)](s) = \varepsilon _0\left( B_1\frac{s^{\alpha -1}}{s^{\alpha }+A_0} + B_0\frac{s^{-1}}{s^{\alpha }+A_0} \right) . \end{aligned}$$
(3.5)

Coming back to the time domain with the use of Proposition 2.1, we obtain

$$\begin{aligned} \sigma _1(t) = \varepsilon _0\left( B_1 Z_{\alpha ,1}(t;-A_0) + B_0 Z_{\alpha ,1+\alpha }(t;-A_0)\right) . \end{aligned}$$
(3.6)

Next we proceed with the second term \(\varepsilon _2\) of the signal; thus, we have

$$\begin{aligned} \frac{\mathrm{{d}}^{\alpha }}{\mathrm{{d}}t^{\alpha }}\sigma _2(t) + A_0\sigma _2(t) = B_1\frac{\mathrm{{d}}^{\alpha }}{\mathrm{{d}}t^{\alpha }}\varepsilon _2(t) + B_0\varepsilon _2(t). \end{aligned}$$
(3.7)

Keeping in mind that \(\varepsilon _2\) vanishes at \(t=0\), we get now

$$\begin{aligned} \mathcal {L}[\sigma _2(t)](s) = \left( B_1\frac{s^{\alpha -1}}{s^{\alpha }+A_0} + B_0\frac{s^{-1}}{s^{\alpha }+A_0} \right) s\mathcal {L}[\varepsilon _2(t)](s). \end{aligned}$$
(3.8)

Applying the inverse Laplace transform and using Borel’s theorem for the Laplace transform of a convolution leads to

$$\begin{aligned} \sigma _2(t) =\int _{0}^{t}B_1 Z_{\alpha ,1}(t-\tau ;-A_0)\varepsilon '_2(\tau )\mathrm {d}\tau +\int _{0}^{t}B_0 Z_{\alpha ,1+\alpha }(t-\tau ;-A_0)\varepsilon '_2(\tau )\mathrm {d}\tau . \end{aligned}$$
(3.9)

Since the only part of \(\varepsilon \) that is responsible for changes is \(\varepsilon _2\), we have \(\varepsilon '(t) = \varepsilon '_2(t)\) for \(t>0\). Then, we get the final stress–strain relationship on the basis of (3.6) and (3.9)

$$\begin{aligned} \sigma (t) = \varepsilon _0 k(t) + \int _{0}^{t}k(t-\tau )\varepsilon '(\tau )\mathrm {d}\tau , \end{aligned}$$
(3.10)
Fig. 1
figure 1

The input signal \(\varepsilon (t)\) and its decomposition into constant part \(\varepsilon _1(t)\) and continuous part \(\varepsilon _2(t)\)

Full size image

with the kernel k given in the form

$$\begin{aligned} k(t)&= B_1 Z_{\alpha ,1}(t;-A_0) + B_0 Z_{\alpha ,1+\alpha }(t;-A_0) = B_1E_{\alpha ,1}(-A_0 t^{\alpha })+B_0 t^{\alpha }E_{\alpha ,\alpha +1}(-A_0 t^{\alpha }). \end{aligned}$$
(3.11)

Using Eq. (2.10), we can rewrite it in a more compact way:

$$\begin{aligned} k(t) = \left( B_1-\frac{B_0}{A_0}\right) E_{\alpha ,1}(-A_0 t^{\alpha })+\frac{B_0}{A_0}. \end{aligned}$$
(3.12)

Then, we have

$$\begin{aligned} \sigma (t) = \mu _0\varepsilon (t)+\varepsilon _0G(t)+\int _{0}^{t}G(t-\tau )\varepsilon '(\tau )\mathrm {d}\tau , \end{aligned}$$
(3.13)

where \(\mu _0=B_0/A_0\) and G is the so-called viscoelastic relaxation function defined as

$$\begin{aligned} G(t) = \mu _1E_{\alpha ,1}(-A_0 t^{\alpha })=\mu _1\sum _{k=0}^{\infty }\frac{\left( -A_0 t^{\alpha }\right) ^k}{\varGamma (\alpha k+1)}, \end{aligned}$$
(3.14)

with parameter \(\mu _1=B_1-\mu _0\). The asymptotic behaviour of the Mittag-Leffler function for arbitrary negative argument with \(0<\alpha <1\) can be described in the following way [12, 21]

$$\begin{aligned} E_{\alpha ,1}\left( -x\right) =1-\frac{x}{\varGamma (1+\alpha )}+\mathcal {O}(x^2), \end{aligned}$$
(3.15)

for \(x\rightarrow 0\), and

$$\begin{aligned} E_{\alpha ,1}\left( -x\right) =\mathcal {O}\left( \frac{1}{x}\right) , \end{aligned}$$
(3.16)

for \(x\rightarrow +\infty \). Thus, it follows that the relaxation function G defined by (3.14) is able to represent physical properties of relaxation behaviour (i.e. a rapid decrease for small times and a very slow decay for large times) on the basis of only four material parameters \(A_0\), \(B_0\), \(B_1\) and \(\alpha \), which define the so-called continuous relaxation spectrum. The plots of G for different values of parameter \(\alpha \) are illustrated in Fig. 2. The function G has a finite value and a vertical tangent at \(t=0\). Its decrease becomes extremely slow for large values of t if \(\alpha \) is small. However, we have noticed computational difficulty in the numerical evaluation of the relaxation function (3.14) for large negative arguments. This problem arises as a result of summing series of terms with alternating signs using floating-point arithmetic. Therefore, we present another method of calculation for the Mittag-Leffler function, which is based on the continuous relaxation spectrum.

Fig. 2
figure 2

Relaxation function G defined by (3.14) and plotted for parameters \(A_0=0.5\), \(\mu _1=8\) and different values of \(\alpha \)

Full size image

3.3 Integral representation of the Mittag-Leffler function

The concept of a general relation between the complex modulus of a linear viscoelastic system and its spectrum is well-known in the literature. We follow [24] and relate the relaxation function G to the continuous relaxation spectrum h via

$$\begin{aligned} G(t)=\int _{0}^{\infty }h(v)\mathrm {e}^{-vt}\mathrm {d}v. \end{aligned}$$
(3.17)

In practical applications, where the function G must be calculated numerically, it is more convenient to introduce the so-called cumulative relaxation spectrum:

$$\begin{aligned} h_c(v)=\int _{0}^{v}h(z)\mathrm {d}z, \end{aligned}$$
(3.18)

which is monotonically an increasing function such that \(h_c(0)=0\) and \(h_c(\infty )<\infty \). Then, integrating by parts (3.17), we obtain an alternative representation of the relaxation function:

$$\begin{aligned} G(t)=\int _{0}^{\infty }h_c\left( \frac{v}{t}\right) \mathrm {e}^{-v}\mathrm {d}v. \end{aligned}$$
(3.19)

However, to take advantage of this formula, we have to first answer the question how to determine \(h_c\) corresponding to the fractional Zener model and its analytical solution (3.13), which specifies the one-dimensional stress–strain relation.

In order to describe the relaxation properties of viscoelastic material, the dynamical tests are performed in which the harmonic oscillations are applied to a material specimen, and the resulting stress is measured until a steady-state value is reached. It is common practice in engineering to use complex variables to present the harmonic response. To this end, we assume the complex harmonic function

$$\begin{aligned} f(t)=\varDelta f\cdot \mathrm{e}^{\mathrm {i}\omega t}H(t), \end{aligned}$$
(3.20)

where \(\omega \) is the angular frequency, \(\varDelta f\) is the amplitude and H is the Heaviside function. Applying the Caputo integral operator (2.16) and calculating the fractional derivative of the function f in the stationary case, i.e. for large values of t (for details see [1, 4, 22]), we have

$$\begin{aligned} \frac{\mathrm{{d}}^{\alpha }f(t)}{\mathrm{{d}}t^{\alpha }}=(\mathrm {i}\omega )^{\alpha }\, f(t). \end{aligned}$$
(3.21)

Without loss of generality, we assume \(\varepsilon _0=0\) and consider the complex and stress as

$$\begin{aligned} \overline{\varepsilon }(t)=\varDelta \varepsilon \cdot \mathrm {e}^{\mathrm {i}\omega t}H(t),\ \ \ \overline{\sigma }(t)=\varDelta \sigma \cdot \mathrm {e}^{\mathrm {i}\omega t}H(t). \end{aligned}$$
(3.22)

Then, by inserting a complex-valued deformation process \(\overline{\varepsilon }\) into Eq. (3.13), we have

$$\begin{aligned} \overline{\sigma }(t)=G^{*}(\mathrm {i}\omega )\,\overline{\varepsilon }(t), \end{aligned}$$
(3.23)

with the quantity

$$\begin{aligned} G^{*}(\mathrm {i}\omega )=\mu _0+\mathrm {i}\omega \int _{0}^{\infty }G(\tau )\mathrm {e}^{-\mathrm {i}\omega \tau }\mathrm {d}\tau , \end{aligned}$$
(3.24)

which defines the so-called complex dynamic modulus for a stationary stress response. Taking into account the representation (3.17) of the relaxation function G and carrying out the integration with respect to the variable \(\tau \) yields

$$\begin{aligned} G^{*}(\mathrm {i}\omega )=\mu _0+\mathrm {i}\omega \int _{0}^{\infty }\frac{h(v)}{v+\mathrm {i}\omega }\mathrm {d}v. \end{aligned}$$
(3.25)

The formula (3.25) shows that the complex modulus \(G^{*}\) and relaxation spectrum h are related to each other. If a relaxation spectrum is given, the complex dynamic modulus is determined. On the other hand, we notice that the function \((G^{*}(i\omega )-\mu _0)/i\omega \) is the Stieltjes transformation of the relaxation spectrum h, i.e.

$$\begin{aligned} S_h(\mathrm {i}\omega )=\frac{G^{*}(\mathrm {i}\omega )-\mu _0}{\mathrm {i}\omega }=\int _{0}^{\infty }\frac{h(v)}{v+\mathrm {i}\omega }\mathrm {d}v. \end{aligned}$$
(3.26)

Assuming that h is an absolutely integrable function on [0, R], for every finite \(R>0\), one may calculate the inverse of the Stieltjes transformation using the formula

$$\begin{aligned} h(v)&=\frac{1}{2\pi \mathrm {i}}\lim _{\xi \rightarrow 0^{+}}\left( S_h(-v-\mathrm {i}\xi )-S_h(-v+\mathrm {i}\xi )\right) \nonumber \\&=\frac{1}{2\pi \mathrm {i}}\lim _{\xi \rightarrow 0^{+}}\left[ \frac{G^{*}(-v-\mathrm {i}\xi )}{-v-i\xi }-\frac{G^{*}(-v+\mathrm {i}\xi )}{-v+\mathrm {i}\xi } +\mu _0\left( \frac{1}{-v+\mathrm {i}\xi }-\frac{1}{-v-\mathrm {i}\xi }\right) \right] , \end{aligned}$$
(3.27)

where v is a positive value for which the function h is defined. It is convenient to express the complex arguments \(-v\pm \mathrm {i}\xi \) in the form of the complex exponential functions

$$\begin{aligned} -v\pm \mathrm {i}\xi =\sqrt{v^2+\xi ^2}\,\mathrm {e}^{\pm (\pi -\arctan (\xi /v))}. \end{aligned}$$
(3.28)

Then, calculating the limit \(\xi \rightarrow 0^{+}\), we obtain the general formula

$$\begin{aligned} h(v)&=\frac{1}{2\pi \mathrm {i}}\left( \frac{G^{*}(v\mathrm{e}^{-\mathrm {i}\pi })}{v\mathrm{e}^{-\mathrm {i}\pi }}-\frac{G^{*}(v\mathrm{e}^{\mathrm {i}\pi })}{v\mathrm{e}^{\mathrm {i}\pi }}\right) =\frac{1}{2v\pi \mathrm {i}}\left( G^{*}(v\mathrm{e}^{\mathrm {i}\pi })-G^{*}(v\mathrm{e}^{-\mathrm {i}\pi })\right) , \end{aligned}$$
(3.29)

which can be used to compute the continuous relaxation spectrum if the complex dynamic modulus is known.

Moreover, bearing in mind (3.21) and inserting the harmonic deformation \(\overline{\varepsilon }\) in combination with the harmonic stress \(\overline{\sigma }\) into (3.1), we transform the fractional Zener model into the frequency domain. Thus, we obtain again the expression (3.23), where the complex dynamic modulus has a form

$$\begin{aligned} G^{*}(\mathrm {i}\omega )=\frac{B_0+B_1(\mathrm {i}\omega )^{\alpha }}{A_0+(\mathrm {i}\omega )^{\alpha }}. \end{aligned}$$
(3.30)

The formula (3.29) in combination with (3.30) can be applied to calculate the relaxation spectrum h of the function G given by the Mittag-Leffler function (3.14). We obtain

$$\begin{aligned} h(v)=\frac{1}{2\pi v \mathrm {i}}\left( \frac{B_0+B_1\,v^{\alpha }\mathrm {e}^{\mathrm {i}\alpha \pi }}{A_0+v^{\alpha }\mathrm {e}^{\mathrm {i}\alpha \pi }}-\frac{B_0+B_1\,v^{\alpha }\mathrm {e}^{-\mathrm {i}\alpha \pi }}{A_0+v^{\alpha }\mathrm {e}^{-\mathrm {i}\alpha \pi }}\right) , \end{aligned}$$
(3.31)

which finally leads to

$$\begin{aligned} h(v)=\frac{A_0\mu _1\sin (\alpha \pi )v^{\alpha }}{\pi v\left( A_0^2+2A_0\cos (\alpha \pi )v^{\alpha }+v^{2\alpha }\right) }. \end{aligned}$$
(3.32)

For further calculations, it is useful to consider the cumulative relaxation spectrum \(h_c\) given by (3.18). Then, analytical integration of function (3.32) yields the following formula

$$\begin{aligned} h_c(v)=\frac{\mu _1}{\alpha \pi }\left[ \arctan \left( \frac{v^{\alpha }}{A_0\sin (\alpha \pi )}+\cot (\alpha \pi )\right) +\pi \left( \alpha -\frac{1}{2}\right) \right] . \end{aligned}$$
(3.33)

This result provides an interesting formula for the efficient numerical calculation of the Mittag-Leffler function \(E_{\alpha ,1}\) for large negative arguments. Indeed, in combination with (3.19) and (3.33), we can formulate the following corollary.

Corollary 3.1

Under the conditions \(x<0\) and \(0<\alpha <1\), the Mittag-Leffler function \(E_{\alpha ,1}\), which occurs as the relaxation function (3.14) in the analytical solution (3.13) of the fractional Zener model (3.1), has the integral representation

$$\begin{aligned} E_{\alpha ,1}(x)=\frac{1}{\alpha \pi }\int _{0}^{\infty }\left[ \arctan \left( \frac{v^{\alpha }}{-x\sin (\alpha \pi )}+\cot (\alpha \pi )\right) +\pi \left( \alpha -\frac{1}{2}\right) \right] \mathrm {e}^{-v}\mathrm {d}v. \end{aligned}$$
(3.34)

3.4 Numerical evaluation of the Mittag-Leffler function

In order to describe the relaxation behaviour of the viscoelastic constitutive model (3.1), we have to evaluate the Mittag-Leffler function \(E_{\alpha ,1}\) for arbitrary negative arguments with \(0<\alpha <1\). It can be represented either by formula (3.14) or (3.34). In each case, the computation of the Mittag-Leffler function with the prescribed accuracy \(\varepsilon >0\) is proved in the following theorems.

Theorem 3.1

Under the conditions \(x<0\), \(\left| x\right| <1\) and \(0<\alpha <1\), the Mittag-Leffler function \(E_{\alpha ,1}\) can be computed with accuracy \(\varepsilon >0\) by the formula

$$\begin{aligned} E_{\alpha ,1}(x)=\sum _{k=0}^{N}\frac{x^k}{\varGamma (\alpha k+1)}+\overline{E}(x,N), \end{aligned}$$
(3.35)

where \(\left| \overline{E}(x,N)\right| \le \varepsilon \) and

$$\begin{aligned} N=\max \left\{ 1,\left\lceil \frac{\ln \left( \varepsilon (1-\left| x\right| )\right) }{\ln (\left| x\right| )}\right\rceil -1\right\} . \end{aligned}$$
(3.36)

Proof

Let \(x<0\) and \(0<\alpha <1\). On the basis of (3.14), we write

$$\begin{aligned} E_{\alpha ,1}(x)&=\sum _{k=0}^{n}\frac{x^k}{\varGamma (\alpha k+1)}+\sum _{k=n+1}^{\infty }\frac{x^k}{\varGamma (\alpha k+1)} = \sum _{k=0}^{n}\frac{x^k}{\varGamma (\alpha k+1)}+\overline{E}(x,n), \end{aligned}$$
(3.37)

for \(n\ge 1\). Since \(\varGamma (k\alpha +1)\ge 1\) for all \(k\ge 1\), we have

$$\begin{aligned} \left| \overline{E}(x,n)\right|&=\left| \sum _{k=n+1}^{\infty }\frac{x^k}{\varGamma (\alpha k+1)}\right| \le \sum _{k=n+1}^{\infty }\left| x\right| ^k = \left| x\right| ^{n+1}\frac{1}{1-|x|}, \end{aligned}$$
(3.38)

for \(\left| x\right| <1\). Thus, the estimate \(\left| \overline{E}(x,n)\right| \le \varepsilon \) follows from the inequality

$$\begin{aligned} n\ge \left\lceil \frac{\ln \left( \varepsilon (1-\left| x\right| )\right) }{\ln (\left| x\right| )}\right\rceil -1, \end{aligned}$$
(3.39)

and \(0<\left| x\right| \le q<1\). \(\square \)

Theorem 3.2

Under the conditions \(x<0\) and \(0<\alpha <1\), the Mittag-Leffler function \(E_{\alpha ,1}\) can be computed with accuracy \(\varepsilon >0\) by the formula

$$\begin{aligned} E_{\alpha ,1}(x)=\frac{1}{\alpha \pi }\int _{0}^{M}\left[ \arctan \left( \frac{v^{\alpha }}{-x\sin (\alpha \pi )}+\cot (\alpha \pi )\right) +\pi \left( \alpha -\frac{1}{2}\right) \right] \mathrm {e}^{-v}\mathrm {d}v+\overline{E}(x,M), \end{aligned}$$
(3.40)

where \(\left| \overline{E}(x,M)\right| \le \varepsilon \) and

$$\begin{aligned} M=\left\{ \begin{array}{lll} \max \left\{ 1,\ln \left( \frac{1}{\varepsilon }\right) \right\} , &{}\quad 0.5\le \alpha<1,\\ \max \left\{ 1,\ln \left( \frac{1-\alpha }{\alpha \varepsilon }\right) \right\} , &{}\quad 0<\alpha <0.5. \end{array}\right. \end{aligned}$$
(3.41)

Proof

Let \(x<0\) and \(0<\alpha <1\). On the basis of (3.34), we have

$$\begin{aligned} E_{\alpha ,1}(x)=\frac{1}{\alpha \pi }\int _{0}^{m}\left[ \arctan \left( \frac{v^{\alpha }}{-x\sin (\alpha \pi )}+\cot (\alpha \pi )\right) +\pi \left( \alpha -\frac{1}{2}\right) \right] \mathrm {e}^{-v}\mathrm {d}v+\overline{E}(x,m), \end{aligned}$$
(3.42)

where

$$\begin{aligned} \overline{E}(x,m)=\frac{1}{\alpha \pi }\int _{m}^{\infty }\left[ \arctan \left( \frac{v^{\alpha }}{-x\sin (\alpha \pi )}+\cot (\alpha \pi )\right) +\pi \left( \alpha -\frac{1}{2}\right) \right] \mathrm {e}^{-v}\mathrm {d}v, \end{aligned}$$
(3.43)

for \(m>0\). Since

$$\begin{aligned}&\left| \arctan \left( \frac{v^{\alpha }}{-x\sin (\alpha \pi )}+\cot (\alpha \pi )\right) +\pi \left( \alpha -\frac{1}{2}\right) \right| {}\le \frac{\pi }{2}+\pi \left| \alpha -\frac{1}{2}\right| , \end{aligned}$$
(3.44)

we notice that

$$\begin{aligned} \left| \overline{E}(x,m)\right|&\le \frac{1}{\alpha }\int _{m}^{\infty }\left( \frac{1}{2}+\left| \alpha -\frac{1}{2}\right| \right) \mathrm {e}^{-v}\mathrm {d}v = \left\{ \begin{array}{ll} \mathrm {e}^{-m}, &{} \quad 0.5\le \alpha<1\\ \left( \frac{1-\alpha }{\alpha }\right) \mathrm {e}^{-m}, &{} \quad 0<\alpha <0.5. \end{array}\right. \end{aligned}$$
(3.45)

Thus, the estimate \(\left| \overline{E}(x,m)\right| \le \varepsilon \) follows from the inequality

$$\begin{aligned} m\ge \left\{ \begin{array}{ll} \ln \left( \frac{1}{\varepsilon }\right) , &{}\quad 0.5\le \alpha<1,\\ \ln \left( \frac{1-\alpha }{\alpha \varepsilon }\right) , &{}\quad 0<\alpha <0.5. \end{array}\right. \end{aligned}$$
(3.46)

and the need to ensure the positive value of parameter m. \(\square \)

From a practical and applicable point of view, we distinguish two cases for the numerical computation of \(E_{\alpha ,1}(x)\) with the prescribed accuracy \(\varepsilon >0\):

  1. (i)

    \(x<0\), \(\left| x\right| \le q<1\),

  2. (ii)

    \(x<0\), \(\left| x\right| > q\), \(q<1\),

where q is a fixed number. In case (i), we apply the series (3.35), whereas in case (ii), we use the integral representation (3.40). Since the number of terms in the sum of formula (3.35) in Theorem 3.1 depends on x, it is recommended to take a number q not very close to 1. Indeed, on the basis of (3.36), we can notice that the smaller value of q is taken, the smaller number of terms N is used in formula (3.35).

Fig. 3
figure 3

Relaxation function G defined by (3.14) (Mittag-Leffler function \(E_{\alpha ,1}\)) and evaluated according to (3.35) and (3.40) for parameters \(q=0.8\), \(A_0=0.5\), \(\mu _1=8\), different values of \(\alpha \) and accuracy \(\varepsilon =2.2204 \times 10^{-16}\)

Full size image
Table 1 Number of terms N in the numerical evaluation of the function G using formula (3.35) with parameters \(q=0.8\), \(A_0=0.5\), \(\mu _1=8\), \(\alpha =0.1\) and accuracy \(\varepsilon =2.2204 \times 10^{-16}\)
Full size table

Using the above approach, we can quite easily evaluate the value of the relaxation function G given by the relation

$$\begin{aligned} G(t) = \mu _1E_{\alpha ,1}(-A_0 t^{\alpha }). \end{aligned}$$
(3.47)

Defining \(T=\left( q/A_0\right) ^{1/\alpha }\) for given \(q<1\), the Mittag-Leffler function is numerically calculated by formula (3.35) for \(0<t\le T\) and (3.40) for \(t>T\), respectively. Our numerical results for arbitrary values of t, with parameters \(q=0.8\), \(A_0=0.5\), \(\mu _1=8\), different values of \(\alpha \) and accuracy \(\varepsilon =2.2204 \times 10^{-16}\) (\(=\) machine epsilon), are plotted in Fig. 3. We have produced them using the programming software Matlab. Moreover, the illustrative values of N corresponding to given times t (and \(x=|-A_0 t^{\alpha }|\)) are placed in Table 1.

4 Conclusions

In this paper, we present the computational aspects of the investigation of relaxation properties of viscoelastic materials. The constitutive Zener model is formulated by means of fractional-order derivatives and subjected to arbitrary and continuous signals with a jump at the origin. The corresponding relaxation function is described by the Mittag-Leffler function in terms of a power series. The relaxation function is defined for negative arguments and preserves stretched exponential behaviour in time. For the numerical point of view, the computational problem arises during numerical evaluation of this function for large negative arguments. We propose a method which allows us to avoid this difficulty. Our approach is based on the integral representation of the Mittag-Leffler function which is easier to handle numerically in such a case. The appropriate formulas for numerical computation of the Mittag-Leffler function with the prescribed accuracy are proved. Finally, a numerical example is demonstrated to illustrate the effectiveness of the presented method.