Effect of anisotropic permeability on convective heat transfer through a porous river bed underlying a fluid layer

Abstract

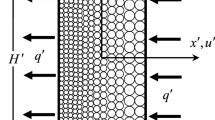
A study is made of convective heat transfer through packed porous beds which consist of a horizontal fluid layer (river bed) and a porous zone with anisotropic permeability and underlaid by a surface heated to a constant temperature $T_1$. The free surface of the fluid layer overlying the horizontal porous layer is heated isothermally at temperature $T_2$ ($>T_1$). Using the Navier–Stokes model for the fluid layer and the generalized Brinkman-extended Darcy model for the porous zone, an exact solution is found for a fully developed system of forced convective flow through the superposed layers. The Beavers–Joseph condition is applied at the interface between the two layers. The influence of hydrodynamic anisotropy on the convective phenomenon is investigated analytically. It is shown that the anisotropic permeability ratio $K^*$, the inclination angle of the principal axes $\varphi$ of the porous medium, and the thickness of the porous lining $\epsilon$ have a strong influence on the convective flow and the heat transfer rate. This analysis helps to predict environmental aquatic behavior.