Skip to main content
SpringerLink
Log in

Two-layer flow in a corrugated channel

  • Published:
Journal of Engineering Mathematics Aims and scope Submit manuscript

Abstract

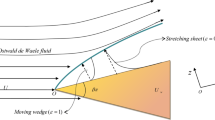
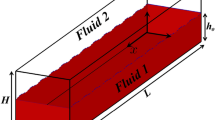
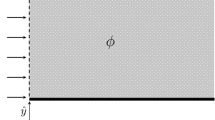
The flow of two superposed viscous fluid layers in a two-dimensional channel confined between a plane and a wavy or indented wall is studied by analytical and numerical methods at arbitrary Reynolds numbers. The interface between the two fluids may exhibit constant or variable surface tension due to an insoluble surfactant. The flow is computed from a specified initial condition using the immersed-interface method on a curvilinear grid constructed by conformal mapping. The numerical simulations illustrate the effect of geometrical nonlinearity and reveal that inertia may increase or decrease the amplitude of the interface profile at steady state depending on the flow parameters. Increasing either the Reynolds number or the wall amplitude above a certain threshold value provokes flow instability and overturning of the interface. In the Appendix, a linear perturbation analysis is performed for arbitrary Reynolds numbers on the assumption of small-amplitude sinusoidal undulations, and results for the amplitude and phase shift of the interfacial and surfactant concentration wave are documented for a broad range of flow conditions. It is found that inertia may have a mixed effect on the deformation and phase shift, while the surfactant promotes the deformation of the interface under most conditions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Cabal A, Szumbarski J and Floryan JM (2002). Stability of flow in a wavy channel. J Fluid Mech 457: 191–212

    Article  MATH  ADS  MathSciNet  Google Scholar 

  2. Floryan JM (2005). Two-dimensional instability of flow in a rough channel. Phys Fluids 17(4): 044101

    Article  ADS  Google Scholar 

  3. Wang CY (1981). Liquid film flowing slowly down a wavy incline. AIChE J 27: 207–212

    Article  Google Scholar 

  4. Kang F and Chen K (1995). Gravity-driven two-layer flow down a slightly wavy periodic incline at low Reynolds numbers. Int J Multiphase Flow 21: 501–513

    Article  MATH  Google Scholar 

  5. Pozrikidis C (2003b). Effect of surfactants on film flow down a periodic wall. J Fluid Mech 496: 105–127

    Article  MATH  ADS  MathSciNet  Google Scholar 

  6. Vlachogiannis M and Bontozoglou V (2002). Experiments on laminar film flow along a periodic wall. J Fluid Mech 457: 133–156

    Article  MATH  ADS  Google Scholar 

  7. Wierschem A, Scholle M and Aksel N (2003). Vortices in film flow over strongly undulated bottom profiles at low Reynolds numbers. Phys Fluids 15: 426–435

    Article  ADS  MathSciNet  Google Scholar 

  8. Luo H and Pozrikidis C (2006). Shear-driven and channel flow of a liquid film over a corrugated or indented wall. J Fluid Mech 556: 167–188

    Article  MATH  ADS  MathSciNet  Google Scholar 

  9. Li X and Pozrikidis C (1997). The effect of surfactants on drop deformation and on the rheology of dilute emulsions in Stokes flow. J Fluid Mech 341: 165–194

    Article  MATH  ADS  MathSciNet  Google Scholar 

  10. Pozrikidis C (2001). Interfacial dynamics for Stokes flow. J Comp Phys 169: 250–301

    Article  MATH  ADS  Google Scholar 

  11. Adamson AW (1990). Physical chemistry of surfaces. Wiley, London

    Google Scholar 

  12. Pozrikidis C (2004). Instability of multi-layer channel and film flows. Adv Appl Mech 40: 179–239

    Article  Google Scholar 

  13. Peskin CS (2002). The immersed boundary method. Acta Numerica 11: 479–517

    Article  MATH  MathSciNet  Google Scholar 

  14. Pozrikidis C (2004). Effect of inertia on the Marangoni instability of two-layer channel flow, Part I: numerical simulations. J Engng Math 50: 311–327

    Article  MATH  MathSciNet  Google Scholar 

  15. Blyth MG, Luo H and Pozrikidis C (2006). Stability of axisymmetric core-annular flow in the presence of an insoluble surfactant. J Fluid Mech 548: 207–235

    Article  ADS  MathSciNet  Google Scholar 

  16. Caponi EA, Fornberg B, Knight DD, Mclean JW, Saffman PG and Yuen HC (1982). Calculations of laminar viscous flow over a moving wavy surface. J Fluid Mech 124: 347–362

    Article  MATH  ADS  Google Scholar 

  17. Pozrikidis C (1997). Introduction to theoretical and computational fluid dynamics. Oxford University Press, New York

    MATH  Google Scholar 

  18. Pozrikidis C (2003). On the relationship between the pressure and the projection function for the numerical computation of incompressible flow. Euro J Mech B / Fluids 22: 105–121

    Article  MATH  MathSciNet  ADS  Google Scholar 

  19. Yon S and Pozrikidis C (1998). A finite-volume / boundary-element method for flow past interfaces in the presence of surfactants, with application to shear flow past a viscous drop. Computers and Fluids 27: 879–902

    Article  MATH  Google Scholar 

  20. Luo H and Bewley TR (2004). On the contravariant form of the Navier–Stokes equation in time-dependent curvilinear coordinate systems. J Comp Phys 199(1): 355–375

    Article  MATH  ADS  MathSciNet  Google Scholar 

  21. Blyth MG and Pozrikidis C (2004). Evolution equations for the surface concentration of an insoluble surfactant; stability of an elongating thread and a stretched interface. Theor Comp Fluid Dyn 17(3): 147–164

    Article  MATH  Google Scholar 

  22. Gottlieb D and Orszag SA (1977). Numerical analysis of spectral methods. SIAM, Philadelphia

    MATH  Google Scholar 

  23. Dongarra JJ, Straughan B and Walker DW (1996). Chebyshev tau-QZ algorithm methods for calculating spectra of hydrodynamic stability problems. Appl Num Math 22: 399–434

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical and Aerospace Engineering, George Washington University, Suite T739, 801 22nd St. NW, Washington, DC, 20052, USA

    H. Luo

  2. School of Mathematics, University of East Anglia, Norwich, England, NR4 7TJ, UK

    M. G. Blyth

  3. Department of Mechanical and Aerospace Engineering, University of California, San Diego, La Jolla, CA, 92093-0411, USA

    C. Pozrikidis

Authors
  1. H. Luo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. G. Blyth
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. C. Pozrikidis
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. G. Blyth.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Luo, H., Blyth, M.G. & Pozrikidis, C. Two-layer flow in a corrugated channel. J Eng Math 60, 127–147 (2008). https://doi.org/10.1007/s10665-006-9134-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10665-006-9134-2

Keywords

Search

Navigation