Abstract
This paper investigates the validity of the real interest rate parity hypothesis (RIPH) using a panel unit root approach. For this purpose, first we estimate the possible nonlinear data-generating processes of the real interest rate differential series and using these estimates determine which panel unit root test is better for analyzing the RIPH. To this end, smooth transition autoregressive and threshold autoregressive (TAR) models are estimated for two different panels of countries: G7 and post-Soviet transition economies. The results show that the data displays both strong asymmetry and high transition speed. Therefore, secondly, we propose a new panel unit root test where the alternative is stationary with asymmetric TAR adjustment, and provide their empirical power properties. Finally, we demonstrate that our newly proposed test is able to provide conclusive evidence in favor of the RIPH in contrast to the other panel unit root tests considered.


Similar content being viewed by others
Notes
For the PPP hypothesis this occurs because the nominal rates act more like a random walk under a flexible exchange rate regime and the real exchange rates that imitate the behavior of the nominal rates with sticky prices also behave like a random walk and thereby violate the PPP. Sarno (2005) corroborates this argument by empirically demonstrating that the PPP tends to perform better if the exchange rate is fixed. Similarly, the greater monetary independence realized under flexible exchange rates causes the nominal interest rates to act more sluggishly in response to changes in the international rates thereby violating the UIP (Frankel et al. 2004).
These reasons include transmission of monetary shocks across countries due to currency substitution, direct spillover effects in monetary aggregates arising from characterizing money as endogenous, and violation of the UIP due to carry trade.
For instance, Dumas (1992) have showed that sluggish and costly adjustments to deviations from equilibrium in goods markets may bring about real interest rate relationships that are indeed nonlinear.
Connecting exchange rate movements to movements in fundamentals such as the interest rate remains a contentious and daunting issue. Monetary models of the exchange rate (including interest rates) have struggled to account for exchange rate changes even ex post (Rogoff 2001). This implies that the fundamentals which are supposed to drive the exchange rate in theory (namely interest rates in the context of this paper) are characterized by small explanatory power in reality. Certain sample periods have appeared well fitted (Mark 1995), but there has been little consistency as the samples have been extended (Cheung et al. 2005). Some optimism has emerged regarding the longer-run ability of monetary models (MacDonald 1999; Engel et al. 2008), but the vast majority of short term and even longer term movements in exchange rates remain anomalous with the consequence that the hypotheses tested in the paper remain to a certain extent hidden in the data. An important strand of the literature has tried to address this deficiency by allowing for non-linear effects of fundamentals on the exchange rate (or the interest rate). Some of the empirical studies have allowed for recurrent shifts between two regimes in Markov-switching or smooth transition threshold models (Sarantis 1999; Taylor and Peel 2000; Kilian and Taylor 2003). While these approaches led to an improvement over linear models in many cases, non-linear dynamics remained largely unexplained. Others have allowed for stark and unpredictable changes in the relationship based on tests for parameter instability, though with linear relationships within regimes, and have offered notable improvement via these piece-wise linear models (as more recently Belke et al. 2011).
Nonlinear estimations are also carried out for the G20 and emerging countries including Brazil, Chile, China, Mexico, Turkey, India, Indonesia, Malaysia, Thailand, Peru, Philippines, and South Africa. The results obtained for the G20 and emerging countries are similar to those obtained in this study for the G7 and transition countries, respectively. Results are available upon request.
The existence of cross sectional dependence in the real interest rate differential series (RIDs) of the countries included in our sample is formally tested using the cross sectional dependence (CD) tests proposed by Pesaran (2004). All the test results do confirm the existence of CD between the RIDs of the countries in the sample. The results of these tests are available upon request.
We have excluded the three Baltic post-Soviet countries that are also classified as the CEECs that have achieved membership in the EU, namely Latvia, Lithuania and Estonia from our sample. The reason of this choice was to concentrate solely on the past-Soviet countries that try to increase their integration with the rest of the world but have or could not achieve deep bounds with one of the developed countries or blocks like these three CEECs.
If the RIDs converge to a zero mean in the long-run, then the strong version of the RIPH is said to hold. However, as argued in Ferreira and León-Ledesma (2007) and Camarero et al. (2010) a long run-mean that is different from zero may be theoretically justified by the existence of transaction costs, non-traded goods, non-zero country-specific risk premium, or different national tax rates. If this is the case, then the RIPH is said to hold in its weak version. Following Ferreira and León-Ledesma (2007) and Camarero et al. (2010) we have focused on testing the weak version of the RIPH in this study, since it also nests the strong version as a special case.
See Ucar and Omay (2009) for further details.
Equation (6) exhibits only one transition function. The other way of writing Eq. (6) is as follows: \( \Delta y_{it} = \alpha_{i} + \phi_{i} y_{i,t - 1} \left[ {1 - \exp ( - \theta_{i} y_{i,t - d}^{2} )} \right] + \gamma_{i} y_{i,t - 1} \left[ {1 - \left( {1 - \exp ( - \theta_{i} y_{i,t - d}^{2} )} \right)} \right] + \varepsilon_{it} \) [see Teräsvirta (1994) for details]. Our PTAR representation is similar to this representation. In Eq. (6) the lower regime parameter is obtained by adding \( \phi_{i} \) and \( \gamma_{i} \) (i.e., \( \phi_{i} + \gamma_{i} \)) where the upper regime parameter is \( \gamma_{i} \). However, in the above representation there is no need to carry out an addition. The lower regime parameter is given directly by the parameter \( \phi_{i} \) and the upper regime parameter is again represented by \( \gamma_{i} \).
The details are given in the appendix section. For further details please refer to Enders and Granger (1998).
See Omay (2014) for further details about the cross sectional dependence problem.
Refer to Ucar and Omay (2009) for the details of the sieve bootstrap methodology.
We utilized monthly data for the transition countries to increase the number of observations.
For France no data is available for any of these series from 1999Q1 when the Euro was introduced. Following the same methodology used to construct the global vector autoregression (GVAR) database, the country specific IFS money market rate was used from 1979Q1 to 1998Q4 and the series was completed to 2011Q2 using the corresponding data for Germany as the representative euro area interest rate. The GVAR data are publicly available at: https://sites.google.com/site/gvarmodelling/ data, including a detailed description of the data and sources.
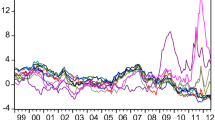
Pesaran et al. (2013) calculates the ex-post real interest rate for each country i using the formula \( r_{it} = 0.25\ln \left[ {1 + \left( {R_{it} /100} \right) - \left( {p_{it} - p_{i,t - 1} } \right)} \right] \) where \( R_{it} \) is the short-term rate of interest per annum in per cent in country \( i \), \( p_{it} = \ln CPI_{it} \) and \( CPI_{it} \) is the consumer price index of country \( i \). The RID for a particular country \( i \) is then calculated according to Eq. (5) by taking the US as the base foreign country.
Moreover, in a panel data setting, finding the threshold parameter using the searching algorithms will lead to a power loses in the proposed test. Enders (2001) also found similar results in the power analysis of the TAR and M-TAR models.
We have also estimated these nonlinear parameters for G20 and emerging economies, and found similar results. The nonlinear parameters are located in between \( \gamma \cong \left\{ {0.90,2.50} \right\} \) for G20 countries and \( \gamma \cong \left\{ {0.90,10000} \right\} \) for the emerging economies. Therefore, the results obtained from the panel unit root tests for G20 (emerging) countries will be similar to those obtained for the G7 (transition) countries. Results are available upon request.
We may also distinguish more explicitly between national and international trends as potential drivers of the RIPH equilibrium following Belke et al. (2011), and Belke and Dreger (2013). To analyze these issues, each variable could be decomposed into common and idiosyncratic components. The idiosyncratic component is the part of a variable that is driven by national developments, whereas the common component represents international trends in the evolution of the variables. The CSD bias can be remedied using 3 alternative methods namely; the Common Correlated Error (CCE) estimator (Pesaran 2006, 2007); the factor structure approach developed by Bai and Ng (2004), known as PANIC (Panel Analysis of Nonstationarity in the Idiosyncratic and Common Components); and sieve bootstrap methodology (Chang 2004). The CCE estimator augments the panel regressions by including the cross-sectional averages of the lagged first-differenced terms, and this approach is valid for panels where N and T are of the same order of magnitude (Pesaran 2007) unlike the principal component approach that requires. Although Kapetanios et al. (2011) have shown that the CCE estimators have better small sample properties than the factor-based estimators, using the CCE estimator in our present context is quite troublesome since our testing procedure utilizes an indicator function that may produce problems while taking the averages of the independent variable. Hence, we prefer to use the bootstrap methodology which also solves the CSD problem in a multifactor error structure. Besides, the bootstrap methodology is shown to be a better remedy for smooth structural break panel unit root tests with CSD, as opposed to the CCE methodology (Omay et al. 2013). Therefore, our methodology is not suitable for obtaining the common trends and idiosyncratic components separately. But, as a further research, PANIC and/or CCE estimators may be used for different forms of nonlinearities which permit the use of these methods.
Taylor and Sarno (1998) emphasized that panel unit root tests may reject joint non-stationarity even if only one of the processes is stationary under the alternative hypothesis. Thus, if the unit root null is rejected, it is important to distinguish between non-stationary and stationary series. See Chortareas and Kapetanios (2009) for the details of the SPSM.
The RIPH was investigated for these countries with respect to also Russia and Germany, and similar results were found. These results are available upon request.
The exchange rate regime of a country can be classified according to either the International Monetary Fund (IMF)’s official, de jure, classification that uses the country’s self-reported exchange rate policies or the actually implemented, de facto, exchange rate policies. As stated in Calvo and Reinhart (2002), Gosh et al. (1997) and Levy-Yeyati and Sturzenegger (2005), the official exchange rate regime adopted by a country can be considerably different from the one that is actually implemented. The country can develop a fear of floating and intervene in the foreign exchange market to prevent the actual variability of its exchange rate or officially follow a pegging regime but adjust its parity very often. These considerations have led researchers to develop alternative measures to identify the de facto exchange rate regimes of the countries. Examples of this approach include Reinhart and Rogoff (2004) and Levy-Yeyati and Sturzenegger (2005). When the de jure classification and the de facto classification of Reinhart and Rogoff (2004) that is updated by Ilzetzki et al. (2011) are both taken into account the following results can be deduced with respect to the exchange rate systems of the countries included in our sample. First, there are important differences between the exchange rate regimes of the G7 and transition countries. Second, the transition economies have more regime changes than the G7 countries. Second, the freely floating regime is observed in the G7 (basically, by the UK, Japan, and Canada) during a considerably large time span under the de jure classification, whereas no country from the transition group has fallen into this category for the de facto classification. Third, while the freely falling regime has been present in all of the transition countries during important lapses of time, in the case of the G7 this regime has happened only in Italy and just for seven months (from 1992:09 to 1993:03). Fourth, the dual markets regime is not observed in the case of the G7 and in the case of the transition countries 120 observations are recorded, with 24 observations corresponding to Georgia, Ukraine and Russia and the remaining 48 being for Moldova. Fifth, a comparison between the de jure and de facto classifications for the transition countries indicates a decreasing use of floating exchange rates in favor of crawling pegs. This differential between the two classifications may justify the fear of floating for the transition economies.
These results depend on the special characteristics of the RID data. The same results will not prevail for other data structures. The MTAR process is very different in nature from the TAR model. For more details see Enders and Granger (1998).
The results of the PMTAR unit root tests, where the threshold is consistently estimated using Chan’s (1993) method, are available upon request.
This result is in line with the finding of Belke et al. (2011) who have found that cointegration exists only among the common components of macroeconomic variables.
We have also generated the critical values for the consistent estimate of the threshold. Tables are available upon request.
The empirical bootstrap program written to implement both the PTAR and PMTAR unit root tests is available upon request.
References
Baharumshah AZ, Haw CT, Fountas S (2005) A panel study on real interest rate parity in East Asian countries: pre- and post-liberalization era. Glob Finance J 16:69–85
Baharumshah AZ, Soon S-V, Borsic D (2013) Real interest parity in Central and Eastern European countries: evidence on integration into EU and the US markets. J Int Financ Mark Inst Money 25:163–180
Bai J, Ng S (2004) A PANIC attack on unit roots and cointegration. Econometrica 72(4):1127–1177
Baillie RT, Kiliç R (2006) Do asymmetric and nonlinear adjustments explain the forward premium anomaly? J Int Money Finance 25:22–47
Balke NS, Wohar ME (1998) Nonlinear dynamics and covered interest parity. Empir Econ 23:535–559
Bansal R, Dahlquist M (2000) The forward premium puzzle: different tales from developed and emerging economics. J Int Econ 51:115–144
Belke A, Dreger C (2013) Current account imbalances in the Euro area: does catching up explain the development? Rev Int Econ 21:6–17
Belke A, Rees A (2014) Globalisation and monetary policy—a FAVAR Analysis for the G7 and the Euro area. N Am J Econ Finance 29:306–321
Belke A, Dobnik F, Dreger C (2011) Energy consumption and economic growth—new insights into the cointegration relationship. Energy Econ 33:782–789
Bilson JFO (1978) Rational expectations and the exchange rate. In: Frenkel JA, Johnson HG (eds) The economics of exchange rates: selected studies. Addison Wesley, New York, p 1978
Calvo GA, Reinhart CM (2002) Fear of floating. Q J Econ 117:379–408
Camarero M, Carrion-i-Silvestre JL, Tamarit C (2010) does real interest rate parity hold for OECD countries? New evidence using panel stationarity tests with cross-section dependence and structural breaks. Scott J Polit Econ 57:568–590
Chan K-S (1993) Consistent and limiting distribution of the least squares estimator of a threshold autoregressive model. Ann Stat 21:520–533
Chang Y (2002) Nonlinear IV unit root tests in panels with cross-sectional dependency. J Econom 110:261–292
Chang Y (2004) Bootstrap unit root tests in panels with cross-sectional dependency. J Econom 120:263–293
Cheung Y-W, Chinn MD, Pascual AG (2005) Empirical exchange rate models of the nineties: are any fit to survive? J Int Money Finance 24:1150–1175
Chortareas G, Kapetanios G (2009) Getting PPP right: identifying mean-reverting real exchange rates in panels. J Bank Finance 33:390–404
Chung YS, Crowder WJ (2004) Why are real interest rates not equalized internationally? South Econ J 71:441–458
Cumby RE, Obstfeld M (1984) International interest rate and price level linkages under flexible exchange rates: a review of recent evidence. In: Bilson JFO, Marston RC (eds) Exchange rate theory and practice. University of Chicago Press, Chicago, pp 121–151
Dreger C (2010) Does the nominal exchange rate regime affect the real interest parity condition? N Am J Econ Finance 21:274–285
Dumas B (1992) Dynamic equilibrium and the real exchange rate in a spatially separated world. Rev Finan Stud 5:153–180
Dutton MM (1993) Real interest rate parity new measures and tests. J Int Money Finance 12:62–77
Elliott G, Jansson M (2003) Testing for unit roots with stationary covariates. J Econom 115:75–89
Enders W (2001) Improved critical values for the Enders-Granger unit-root test. Appl Econom Lett 8:257–261
Enders W, Granger CWJ (1998) Unit root tests and asymmetric adjustment with an example using the term structure of interest rates. J Bus Econ Stat 16:304–311
Engel C, Mark NC, West KD (2008) Exchange rate models are not as bad as you think. In: Acemoglu D, Rogoff K, Woodford M (eds) NBER macroeconomics annual 2007, vol 22. University of Chicago Press, Chicago, pp 281–441
Feldstein M (1982) Domestic savings and international capital movements in the long-run and the short-run. NBER working paper no. 947
Ferreira AL, León-Ledesma MA (2007) Does the real interest parity hypothesis hold? Evidence for developed and emerging markets. J Int Money Finance 26:364–382
Flood RP, Marion NP (1982) The transmission of disturbances under alternative exchange rate regimes with optimal indexing. Q J Econ 97:43–66
Fountas S, Wu J-L (1999) Testing for real interest rate convergence in European countries. Scott J Polit Econ 46:158–174
Frankel JA (1976) A monetary approach to the exchange rate: doctrinal aspects and empirical evidence. Scand J Econ 78:200–224
Frankel JA (1992) Measuring international capital mobility: a review. Am Econ Rev 82:197–202
Frankel JA, Schmukler SL, Servén L (2004) Global transmission of interest rates: monetary independence and currency regime. J Int Money Finance 23:701–733
Fujii E, Chinn MD (2001) Fin de Siècle real interest rate parity. J Int Finan Mark Inst Money 11:289–308
Gosh AR, Gulde A-M, Ostry JD, Wolf Holger C (1997) Does the nominal exchange rate regime matter? Working paper 5874. NBER, Cambridge, MA
Güney PÖ, Hasanov M (2014) Real interest rate parity hypothesis in post-Soviet countries: evidence from unit root tests. Econ Model 36:120–129
Helleiner E, Pauly LW (2014) Part three: global finance. In: Ravenhill J (ed) Global political economy. Oxford University Press, Oxford
Holmes MJ (2002) Does long-run real interest parity hold among EU countries? Some new panel data evidence. Q Rev Econ Finance 42:733–746
Holmes MJ, Maghrebi N (2006) Are international real interest rate linkages characterized by asymmetric adjustment? J Int Finan Mark Inst Money 16:384–396
Ilzetzki E, Reinhart CM, Rogoff KS (2011) Exchange rate arrangements entering the 21st century: which anchor will hold? (unpublished manuscript)
Kapetanios G, Shin Y, Snell A (2003) Testing for a unit root in the nonlinear STAR framework. J Econom 112:359–379
Kapetanios G, Pesaran MH, Yamagata T (2011) Panels with non-stationary multifactor error structures. J Econom 160(2):326–348
Kilian L, Taylor MP (2003) Why is it so difficult to beat the random walk forecast of exchange rates? J Int Econ 60:85–107
Levy-Yeyati E, Sturzenegger F (2005) Classifying exchange rate regimes: deeds vs. words. Eur Econ Rev 49:1603–1635
MacDonald R (1999) Exchange rate behaviour: are fundamentals important? Econ J 109:673–691
Mancuso AJ, Goodwin BK, Grennes TJ (2003) Nonlinear aspects of capital market integration and real interest rate equalization. Int Rev Econ Finance 12:283–303
Mark NC (1985) Some evidence on the international inequality of real interest rates. J Int Money Finance 4:189–208
Mark NC (1995) Exchange rates and fundamentals: evidence on long-horizon predictability. Am Econ Rev 85:201–218
Mishkin FS (1984) Are real interest rates equal across countries? An empirical investigation of international parity conditions. J Finance 39:1345–1357
Obstfeld M, Taylor AM (2002) Globalization and capital markets. NBER working paper no. 8846
Omay T (2014) A survey about bias reduction in smooth transition panel data analysis. Econom Lett 1:18–42
Omay T, Hasanov M, Shin Y (2013) Testing unit root in heterogeneous panels with trend-break. A conference on cross-sectional dependence in panel data models. Cambridge University, Cambridge
Pesaran MH (2004) General diagnostic tests for cross-section dependence in panels. In: Cambridge working papers in economics 0435. Faculty of Economics, University of Cambridge, Cambridge
Pesaran MH (2006) Estimation and inference in large heterogeneous panels with a multifactor error structure. Econometrica 74:967–1012
Pesaran MH (2007) A simple panel unit root test in the presence of cross-section dependence. J Appl Econom 22(2):265–312
Pesaran MH, Smith LV, Yagamata T (2013) Panel unit root tests in the presence of a multifactor error structure. J Econom 175:94–115
Rapach DE, Weber CE (2004) Are real interest rates really nonstationary? New evidence from tests with good size and power. J Macroecon 26:409–430
Reinhart CM, Rogoff KS (2004) The modern history of exchange rate arrangements: a reinterpretation. Q J Econ 119:1–48
Rogoff KD (2001) The failure of empirical exchange rate models: no longer new but still true. Econ Policy Web Essay 1(1)
Sarantis N (1999) Modeling nonlinearities in real effective exchange rates. J Int Money Finance 18:27–54
Sarno L (2005) Towards a solution to the puzzles in exchange rate economics: where do we stand? Can J Econ 38:673–708
Singh M, Banerjee A (2006) Testing real interest parity in emerging markets. International monetary fund working paper, no. WP/06/249
Taylor AM (2001) Potential pitfalls for the purchasing-power-parity puzzle? Sampling and specification biases in mean-reversion tests of the law of one price. Econometrica 69:473–498
Taylor MP, Peel DA (2000) Nonlinear adjustment, long-run equilibrium and exchange rate fundamentals. J Int Money Finance 19:33–53
Taylor MP, Sarno L (1998) The behaviour of real exchange rates during the post-Bretton woods period. J Int Econ 46:281–312
Teräsvirta T (1994) Specification, estimation, and evaluation of smooth transition autoregressive models. J Am Stat Assoc 89:208–218
Tsong C-C, Lee C-F (2013) Further evidence on real interest rate equalization: panel information, non linearities and structural changes. Bull Econ Res 65:85–105
Ucar N, Omay T (2009) Testing for unit roots in nonlinear heterogeneous panels. Econ Lett 104:5–8
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Consider the following PTAR(1) model:
where \( \tau \) denotes the threshold variable. We have set this variable to zero as in Enders and Granger (1998) and obtained the critical values tabulated in Tables 8 and 9. If \( \rho_{i1} = \rho_{i2} = 0 \) in Eq. (11) then \( y_{it} \) contains a unit root, while if \( \rho_{i1} = \rho_{i2} < 0 \), \( y_{it} \) is a stationary TAR process with symmetric adjustment, and if \( \rho_{i1} < 0,\,\,\rho_{i2} < 0 \) and \( \rho_{i1} \ne \rho_{i2} \), \( y_{it} \) is a stationary TAR process displaying asymmetric adjustment. We propose testing for whether \( y_{it} \) contains a unit root using the F-statistic for testing \( \rho_{i1} = \rho_{i2} = 0 \) in (11), and/or the most significant of the t-statistics from those for testing \( \rho_{i1} = 0 \) and \( \rho_{i2} = 0 \). In a panel framework, for the model given in (11), the relevant \( F \) and t-statistic will be referred to as \( \bar{F}_{1p,\alpha } \) and \( \bar{t}_{1p,\alpha } \). The test statistics are computed through taking the average of individual EG statistics across the whole panel. Also we have generated the critical values for the PMTAR unit root test, but they are very similar to the values reported in Tables 8 and 9. Hence, we do not tabulate them here, but they are available upon request.Footnote 32 , Footnote 33
The threshold values, which are obtained taking the average of the series, can be denoted as follows:
where a denotes the average of the series.
Rights and permissions
About this article
Cite this article
Çorakcı, A., Emirmahmutoglu, F. & Omay, T. Re-examining the real interest rate parity hypothesis (RIPH) using panel unit root tests with asymmetry and cross-section dependence. Empirica 44, 91–120 (2017). https://doi.org/10.1007/s10663-015-9312-4
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10663-015-9312-4