Abstract
Properly sampling soils and mapping soil contamination in urban environments requires that impacts of spatial autocorrelation be taken into account. As spatial autocorrelation increases in an urban landscape, the amount of duplicate information contained in georeferenced data also increases, whether an entire population or some type of random sample drawn from that population is being analyzed, resulting in conventional power and sample size calculation formulae yielding incorrect sample size numbers vis-à-vis model-based inference. Griffith (in Annals, Association of American Geographers, 95, 740–760, 2005) exploits spatial statistical model specifications to formulate equations for estimating the necessary sample size needed to obtain some predetermined level of precision for an analysis of georeferenced data when implementing a tessellation stratified random sampling design, labeling this approach model-informed, since a model of latent spatial autocorrelation is required. This paper addresses issues of efficiency associated with these model-based results. It summarizes findings from a data collection exercise (soil samples collected from across Syracuse, NY), as well as from a set of resampling and from a set of simulation experiments following experimental design principles spelled out by Overton and Stehman (in Communications in Statistics: Theory and Methods, 22, 2641–2660). Guidelines are suggested concerning appropriate sample size (i.e., how many) and sampling network (i.e., where).





Similar content being viewed by others
Notes
TR(V) = n because of the division by C 1/(C 0 + C 1). The denominator contains n 2 because each standardized semivariogram term is subtracted from 1. And, i ≠ j for the summation because n, representing the sum of the diagonal entries, has been placed in a separate term for 1 T V1.
This experiment was repeated several times to confirm the stability of the variance estimates.
References
Anselin, L. (1988). Spatial econometrics: methods and models. Dordrecht: Martinus Nijhoff.
Cressie, N. (1991). Statistics for spatial data. New York: Wiley.
Griffith, D. (1988). Advanced spatial statistics. Dordrecht: Martinus Nijhoff.
Griffith, D. (1992). Simplifying the normalizing factor in spatial autoregressions for irregular lattices. Papers in Regional Science, 71, 71–86.
Griffith, D. (2000). A linear regression solution to the spatial autocorrelation problem. Journal of Geographical Systems, 2, 141–156.
Griffith, D. (2003). Spatial autocorrelation and spatial filtering: gaining understanding through theory and scientific visualization. Berlin: Springer.
Griffith, D. (2005). Effective geographic sample size in the presence of spatial autocorrelation. Annals, Association of American Geographers, 95, 740–760.
Griffith, D. (2006). Statistical efficiency of model-informed geographic sampling designs. In C. Mário, & M. Painho (Eds.), Proceedings of accuracy 2006, Proceedings of the 7th international symposium on spatial accuracy assessment in a natural resources and environmental sciences. Lisboa, Portugal: Instituto Geográfico Português, pp. 91–98.
Grondona, M., & Cressie, N. (1991). Using spatial considerations in the analysis of experiments. Technometrics, 33, 381–392.
de Gruijter, J., Brus, D., Bierkens, M., & Knotters, M. (2006). Sampling for natural resource monitoring. New York: Springer.
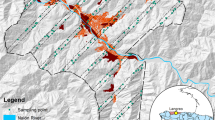
Johnson, D., Hager, J., Hunt, A., Griffith, D., Blount, S., Ellsworth, S., Hintz, J., Lucci, R., Mittiga, A., Prokhorova, D., Tidd, L., Millones, M., & Vincent, M. (2005). Field methods for mapping urban metal distributions in house dusts and surface soils of Syracuse, NY, USA, Science in China (Series C: Life Sciences), 48 (Suppl.), pp. 192–199.
Kelly, K., & Maxwell, S. (2003). Sample size for multiple regression: obtaining regression coefficients that are accurate, not simply significant. Psychological Methods, 8, 305–321.
Levy, P., & Lemeshow, S. (1991). Sampling of populations: methods and applications. New York: Wiley.
Müller, W. (2001). Collecting spatial data: optimum design of experiments for random fields (2nd ed.). Heidelberg: Physica-Verlag.
Overton, W., & Stehman, S. (1993). Properties of designs for sampling continuous spatial resources from a triangular grid. Communications in Statistics: Theory and Methods, 22, 2641–2660.
Thompson, S. (1992). Sampling. NY: Wiley.
Author information
Authors and Affiliations
Corresponding author
Additional information
This research was supported in part by the National Science Foundation under grant BCS-0552588. The author is an Ashbel Smith Professor.
Appendices
Appendix A: Features of a model-informed sampling design
Design-based spatial sampling (de Gruijter et al. 2006) involves repeatedly sampling locations from a geographic landscape. Tessellation stratified spatial random sampling, advanced by Overton and Stehman (1993), involves partitioning a surface into n mutually exclusive and collectively exhaustive equal-size areal units (i.e., tessellation cells; in their case, hexagons), and then sampling a single location from each tessellation cell. The resulting response variable mean, \(\bar{{y}},\) is computed in a standard way, with its standard variance calculation ignoring the presence of spatial autocorrelation and accompanying variance inflation. The sampling variability is based solely on selecting different locations, and hence different y i values. Normality is achieved via the central limit theorem.
Model-based spatial sampling (de Gruijter et al. 2006) involves repeated realizations via a specified model for a given set of locations selected from a geographic landscape. Tessellation stratified spatial random sampling involves fixing a set of locations, one for each tessellation cell, and then calculating a model mean response whose specification includes a term that accounts for the presence of spatial autocorrelation. Normality is achieved via an assumption about the model error term.
A model-informed tessellation stratified sampling design integrates these two approaches into a hybrid, with the mean response being defined as follows [employing a simultaneous autoregressive (SAR) model specification]:
where Y is an n-by-1 vector of sample location values, W is an n-by-n geographic weights matrix (see “Variance inflation and effective sample size”), μ is the model mean, and ρ is the spatial autoregressive (i.e., autocorrelation) parameter. Variation for both \(\bar{{y}}\) and WY/n relates to design-based sampling, whereas the variability of \(\hat{\mu}\) (a generalized least-squares estimator of μ), which is a function of the model error variance σ 2, relates to model-based sampling. Writing the sample mean in this fashion increases the precision of the estimation. The variance estimate is reduced by \(\frac{\sum\nolimits_{i=1}^n {(1-\rho \lambda _{i})^{2}}}{n}.\) The design-based sampling variability component is further reduced by, roughly, ρ 2. The model-based variability component is increased by 1/(1 − ρ)2, but when combined with \(\hat{\sigma}^{2}\), experiences a net reduction that can be sizable (depending upon the magnitude of ρ). These different components are the sources of variance inflation.
This model-informed tessellation stratified sampling design is in keeping with the perspective of Grondona and Cressie (1991), who show that incorporating spatial modeling into the analysis of agricultural field trial experiments tends to yield statistically more efficient estimators than does the classical approach that ignores latent spatial autocorrelation.
Appendix B: Planned sample size in regression
Griffith (2005) furnishes a formula for determining the effective sample size in the presence of positive spatial autocorrelation. A pure spatial autoregressive model has an associated pseudo-R 2 value that relates to the R 2 value of ordinary least squares. Kelley and Maxwell (2003) survey methods of a priori sample size determination for regression analyses. A pure spatial autoregressive model contains a single covariate, the spatial lag term. Accordingly, their Eq. (2) becomes, for a 95% confidence interval and a width of 0.1 for the autocorrelation parameter estimate,
which approximately equals 386 when a single covariate is uncorrelated with the response variable Y.
Assuming that the autoregressive parameter equals the square root of R 2, which is an oversimplification but not an unreasonable assumption, an overlay of the sample size for a bivariate regression and the effective sample size from a spatial autoregression are portrayed in Fig. 6. The nonlinear nature of the autoregressive model specification is conspicuous in the figure. Nevertheless, they both display a monotonic decline with increasing R 2. In other words, as the percentage of redundant information in georeferenced data increases, the effective sample size decreases as does the necessary sample size for estimating a spatial regression model having a predetermined level of significance for its spatially varying covariates.
Rights and permissions
About this article
Cite this article
Griffith, D.A. Geographic sampling of urban soils for contaminant mapping: how many samples and from where. Environ Geochem Health 30, 495–509 (2008). https://doi.org/10.1007/s10653-008-9186-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10653-008-9186-5