Modeling stratified suspension concentration distribution in turbulent flow using fractional advection–diffusion equation

Abstract

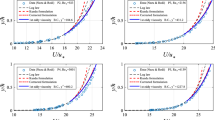
The distribution of suspended sediment particles in a steady, uniform and stratified turbulent flow through open-channels is investigated in this study using fractional advection–diffusion equation (FADE). Unlike previous studies on FADE, the FADE is employed with the effects of stratification due to the presence of the sediment particles. Analogous to the approach of stratified flow, the effect of stratification is connected with the damping of the sediment diffusivity. A general model of sediment diffusion coefficient in stratified flow is proposed which changes along vertical direction as well as with the order of the fractional derivative. Finally the model of sediment distribution is derived incorporating the effects of non-local transport of particles, stratification, hindered settling velocity and damping of mixing length. The model is solved numerically using the fractional Adams–Bashforth–Moulton method and solutions are validated with the experimental data. The validation results are satisfactory. The variation of the depth average sediment diffusion coefficient and the proposed model of sediment diffusion coefficient with the fractional order $\alpha$ are investigated. The results show that with the decrease of fractional order $\alpha$, the value of depth average sediment diffusion coefficient increases and the depth variable sediment diffusion coefficient shows a overall increases throughout the flow depth. The rationality of the dependence of $\alpha$ on both types of sediment diffusion coefficients have been justified physically. It is also found that the effect of stratification results a decrease both for the suspension distribution and the sediment diffusion coefficient which is consistent with the results using traditional ADE.

Appendix: Some preliminaries on fractional derivatives

It is well-known that there are a number of different kinds of definitions of fractional derivatives exists with their applications in various fields [19, 40]. Each definition has its own advantages and are suitable for applications to different type of problems. Among these the Caputo-type derivative is mostly employed in physical problems as it describes the physical behavior well [8, 40]. The Caputo fractional derivative of a function f(y) is defined as

$$\begin{aligned} \,_a^CD_{y}^{\alpha }f(y) = \frac{1}{\Gamma (n-\alpha )}\int _a^{y}\frac{f^{(n)}(\tau )}{(y-\tau )^{\alpha +1-n}}~d\tau \end{aligned}$$

(27)

where $n-1<\alpha \le n$ and $a\in [-\infty , y)$. When $\alpha =n\in N$, Caputo fractional derivative represents the ordinary integer order derivative of order n i.e. $\,_a^CD_{y}^{n}f(y)=f^{(n)}(y)$. The kernel of this fractional model is $(y-\tau )^{n-\alpha -1}$ which gives a power law function. The Eq. 27 can be considered as a convolution of two functions in the interval [a, y] and can be written as

$$\begin{aligned} \,_a^CD_{y}^{\alpha }f(y) = \frac{df(y)}{dy}*\frac{y^{n-\alpha -1}}{\Gamma (n-\alpha )} \end{aligned}$$

(28)

This indicates that fractional derivative value depends on the derivative of the function over the whole interval [a, y]. Alternately, the Caputo fractional derivative can also be defined using the Riemann–Liouville fractional integral as

$$\begin{aligned} \,_a^CD_{y}^{\alpha }f(y) = \,_a^{RL}J_{y}^{m-\alpha } D_{y}^{m} f(y) \end{aligned}$$

(29)

where $D_y^m=\frac{d^m}{dy^m}$ and $m-1<\alpha \le m$, $y>0$ and $m\in N$. Here $\,_a^{RL}J_{y}^{\alpha }$ denotes the Riemenn–Liouville fractional integral of order $\alpha >0$ which is defined as [40]

$$\begin{aligned} \,_a^{RL}J_{y}^{\alpha }f(y) = \,_a^CD_{y}^{-\alpha }f(y) = \frac{1}{\Gamma (\alpha )}\int _a^{y}f(\tau )(y-\tau )^{\alpha -1}~d\tau \end{aligned}$$

(30)