Selecting a binary Markov model for a precipitation process

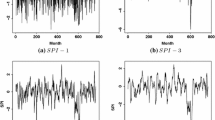
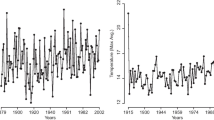
Abstract

This paper uses rth-order categorical Markov chains to model the probability of precipitation. Several stationary and non-stationary high-order Markov models are proposed and compared using BIC. The number of parameters increases exponentially by adding the Markov order. Several classes of high-order Markov models are proposed which their increase of number of parameters are modest. For example models that use the number of precipitation days in a period prior to date, temperature of the previous day and sines/cosines periodic functions (to model the seasonality) are considered. The theory of partial likelihood is used to estimate the parameters. Parsimonious non-stationary first order Markov models with few seasonal terms are found optimal using BIC and temperature does not turn out to be a useful covariate. However BIC seems to underestimate the number of seasonal terms. We have also compared the results with AIC in some cases which tends to pick parsimonious models with more seasonal terms and higher order. We also show that ignoring seasonal terms result in picking higher order Markov chains. Finally we apply the methods to build confidence intervals for the probability of periods with no precipitation or low number of precipitation days in Calgary using historical data from 1980 to 2000.