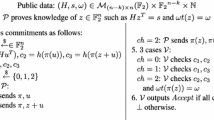Abstract
We present an attack against a code-based signature scheme based on the Lyubashevsky protocol that was recently proposed by Song, Huang, Mu, Wu and Wang (SHMWW). The private key in the SHMWW scheme contains columns coming in part from an identity matrix and in part from a random matrix. The existence of two types of columns leads to a strong bias in the distribution of set bits in produced signatures. Our attack exploits such a bias to recover the private key from a bunch of collected signatures. We provide a theoretical analysis of the attack along with experimental evaluations, and we show that as few as 10 signatures are enough to be collected for successfully recovering the private key. As for previous attempts of adapting Lyubashevsky’s protocol to the case of code-based cryptography, the SHMWW scheme is thus proved unable to provide acceptable security. This confirms that devising secure code-based signature schemes with efficiency comparable to that of other post-quantum solutions (e.g., based on lattices) is still a challenging task.






Similar content being viewed by others
References
Aguilar C., Gaborit P., Schrek J.: A new zero-knowledge code based identification scheme with reduced communication. In: 2011 IEEE Information Theory Workshop, pp 648–652, (2011) https://doi.org/10.1109/ITW.2011.6089577.
Aragon N., Blazy O., Gaborit P., Hauteville A., Zémor G.: Durandal: a rank metric based signature scheme. In: Ishai Y., Rijmen V. (eds.) Advances in Cryptology - EUROCRYPT 2019, pp. 728–758. Springer International Publishing, Cham (2019).
Aragon N., Deneuville J.C., Gaborit, P.: Another code-based adaptation of lyubashevsky’s signature cryptanalysed. Cryptology ePrint Archive, Report 2020/923, (2020) https://eprint.iacr.org/2020/923.
Baldi M., Khathuria K., Persichetti E., Santini P.: Cryptanalysis of a code-based signature scheme based on the Lyubashevsky framework. Cryptology ePrint Archive, Report 2020/905, (2020) https://eprint.iacr.org/2020/905.
Bardet M., Briaud P., Bros M., Gaborit P., Neiger V., Ruatta O., Tillich J.: An algebraic attack on rank metric code-based cryptosystems. In: Advances in Cryptology - EUROCRYPT 2020 Proceedings, Part III, Springer, LNCS, vol 12107, pp 64–93 (2020a).
Bardet M., Bros M., Cabarcas D., Gaborit P., Perlner R.A., Smith-Tone D., Tillich J.P., Verbel J.A.: Improvements of algebraic attacks for solving the rank decoding and MinRank problems. In: Moriai S, Wang H (eds) ASIACRYPT 2020, Part I, Springer, Heidelberg, LNCS, vol 12491, pp 507–536, (2020b) https://doi.org/10.1007/978-3-030-64837-4_17.
Barg S.: Some new NP-complete coding problems. Problemy Peredachi Informatsii 30(3), 23–28 (1994).
Bellini E., Caullery F., Gaborit P., Manzano M., Mateu V.: Improved Veron identification and signature schemes in the rank metric. In: 2019 IEEE International Symposium on Information Theory (ISIT), pp 1872–1876 (2019).
Berlekamp E.R., McEliece R.J., van Tilborg H.C.A.: On the inherent intractability of certain coding problems (corresp.). IEEE Trans. Inf. Theory 24(3), 384–386 (1978). https://doi.org/10.1109/TIT.1978.1055873.
Biasse J.F., Micheli G., Persichetti E., Santini P.: LESS is more: code-based signatures without syndromes. In: Nitaj A., Youssef A. (eds.) Progress in Cryptology - AFRICACRYPT 2020, pp. 45–65. Springer International Publishing, Cham (2020).
Cayrel P.L., Véron P., El Yousfi Alaoui S.M.: A zero-knowledge identification scheme based on the \(q\)-ary syndrome decoding problem. In: Selected Areas in Cryptography. Springer, Berlin, pp 171–186 (2011).
Courtois N., Finiasz M., Sendrier N.: How to achieve a McEliece-based digital signature scheme. In: Boyd C (ed) ASIACRYPT 2001, Springer, Heidelberg, LNCS, vol 2248, pp 157–174, (2001) https://doi.org/10.1007/3-540-45682-1_10.
Debris-Alazard T., Sendrier N., Tillich J.P.: Wave: A new family of trapdoor one-way preimage sampleable functions based on codes. In: Galbraith S.D., Moriai S. (eds) ASIACRYPT 2019, Part I, Springer, Heidelberg, LNCS, vol 11921, pp 21–51, (2019) https://doi.org/10.1007/978-3-030-34578-5_2.
Deneuville J.C., Gaborit P.: Cryptanalysis of a code-based one-time signature. Des. Codes Cryptogr. 88(9), 1857–1866 (2020).
Faugere J.C., Gauthier-Umana V., Otmani A., Perret L., Tillich J.P.: A distinguisher for high-rate mceliece cryptosystems. IEEE Trans. Inf. Theory 59(10), 6830–6844 (2013).
Lyubashevsky V.: Lattice signatures without trapdoors. In: Pointcheval D., Johansson T. (eds) EUROCRYPT 2012, Springer, Heidelberg, LNCS, vol 7237, pp 738–755 (2012) https://doi.org/10.1007/978-3-642-29011-4_43.
Lyubashevsky V., Ducas L., Kiltz E., Lepoint T., Schwabe P., Seiler G., Stehlé D.: CRYSTALS-DILITHIUM. Tech. rep., National Institute of Standards and Technology, available at https://csrc.nist.gov/projects/post-quantum-cryptography/round-2-submissions (2019).
McEliece R.J.: A public-key system based on algebraic coding theory, Jet Propulsion Lab, DSN Progress Report 44, pp 114–116 (1978).
National Institute of Standards and Technology (2017) NIST post-quantum standardization process. https://csrc.nist.gov/Projects/Post-Quantum-Cryptography
Persichetti E.: Improving the efficiency of code-based cryptography. PhD thesis, Department of Mathematics, University of Auckland (2012).
Persichetti E.: Efficient one-time signatures from quasi-cyclic codes: a full treatment. Cryptography 2, 30 (2018). https://doi.org/10.3390/cryptography2040030.
Prange E.: The use of information sets in decoding cyclic codes. IRE Trans. Inf. Theory 8(5), 5–9 (1962).
Rivest R.L., Shamir A., Adleman L.M.: A method for obtaining digital signatures and public-key cryptosystems. Commun. Assoc. Comput. Mach. 21(2), 120–126 (1978).
Santini P., Baldi M., Chiaraluce F.: Cryptanalysis of a one-time code-based digital signature scheme. In: 2019 IEEE International Symposium on Information Theory (ISIT), pp 2594–2598 (2019).
Shor P.W.: Algorithms for quantum computation: Discrete logarithms and factoring. In: 35th FOCS, IEEE Computer Society Press, pp 124–134 (1994) https://doi.org/10.1109/SFCS.1994.365700.
Song Y., Huang X., Mu Y., Wu W., Wang H.: A code-based signature scheme from the Lyubashevsky framework. Theoret. Comput. Sci. 835, 15–30 (2020). https://doi.org/10.1016/j.tcs.2020.05.011.
Stern J.: A new identification scheme based on syndrome decoding. In: Stinson D.R. (ed.) Advances in Cryptology – CRYPTO’ 93, pp. 13–21. Springer, Berlin Heidelberg (1994).
Véron P.: Improved identification schemes based on error-correcting codes. Appl. Algebra Eng. Commun. Comput. 8(1), 57–69 (1997). https://doi.org/10.1007/s002000050053.
Acknowledgements
The authors thank Philippe Gaborit for insightful discussions on preliminary versions of this work.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by M. Albrecht.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was partially funded by the French DGA. Karan Khaturia was supported by University of Zurich Forschungskredit Grant No. FK-19-080. Edoardo Persichetti was supported by the U.S. National Science Foundation Grant CNS-1906360.
Appendix: A computing the number of signatures for a desired confidence level
Appendix: A computing the number of signatures for a desired confidence level
We here prove Proposition 2. To bound the probabilities \(\epsilon _R\) and \(\epsilon _I\) which appear in (4) we will use the Chernoff bound, which we recall in the following.
Theorem 1
Chernoff bound
Let \(X = \sum _{u = 1}^{M}x_u\), where the \(x_u\) are all independent and \(x_u\sim \mathfrak B( \rho )\); then
-
(i)
\(\mathrm {Pr}\left[ X\le (1 - \gamma ) \rho M\right] \le e^{-\frac{\gamma ^2}{2}\rho M}\), for all \(0<\gamma <1\);
-
(ii)
\(\mathrm {Pr}\left[ X\ge (1+\gamma )\rho M\right] \le e^{-\frac{\gamma ^2}{2+\gamma }\rho M}\), for all \(\gamma >0\).
Applying condition (i) of the Chernoff bound on (2), we have \(\rho = \frac{1}{2}\) and \(\gamma = 1-2\delta \), such that
In analogous way, applying condition (ii) of the Chernoff bound on (3), we have \(\rho = \rho _I\) and \(\gamma = \frac{\delta }{\rho _I}-1\), such that
Using these bounds for \(\epsilon _R\) and \(\epsilon _I\), we derive the following inequality on the success probability
We first note that, regardless of the particular choice for \(\delta \), the probabilities \(\epsilon _R^*\) and \(\epsilon _I^*\) decay exponentially with N; thus, we can always choose N sufficiently high to make them extremely low. Using a well known approximation, we have
Now, let
Then, \(N \ge \frac{4}{(1-2\delta )^2} \ln \left( \frac{2\ell (n'-k')}{1-\alpha ^*}\right) \) and (7) implies that
and, \(N \ge \frac{(\delta +\rho _I)}{(\delta -\rho _I)^2} \ln \left( \frac{2\ell k'}{1-\alpha ^*}\right) \) and (8) implies that
Therefore, we obtain the following bound on the probability of success
Rights and permissions
About this article
Cite this article
Aragon, N., Baldi, M., Deneuville, JC. et al. Cryptanalysis of a code-based full-time signature. Des. Codes Cryptogr. 89, 2097–2112 (2021). https://doi.org/10.1007/s10623-021-00902-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10623-021-00902-7