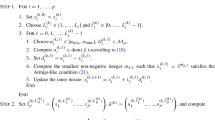Abstract
At each iteration of a block coordinate descent method one minimizes an approximation of the objective function with respect to a generally small set of variables subject to constraints in which these variables are involved. The unconstrained case and the case in which the constraints are simple were analyzed in the recent literature. In this paper we address the problem in which block constraints are not simple and, moreover, the case in which they are not defined by global sets of equations and inequations. A general algorithm that minimizes quadratic models with quadratic regularization over blocks of variables is defined and convergence and complexity are proved. In particular, given tolerances \(\delta >0\) and \(\varepsilon >0\) for feasibility/complementarity and optimality, respectively, it is shown that a measure of \((\delta ,0)\)-criticality tends to zero; and the number of iterations and functional evaluations required to achieve \((\delta ,\varepsilon )\)-criticality is \(O(\varepsilon ^{-2})\). Numerical experiments in which the proposed method is used to solve a continuous version of the traveling salesman problem are presented.







Similar content being viewed by others
Data availability
The authors confirm that all data generated or analyzed in the development of this work are adequately included or referenced in the article itself.
Notes
We already shown, in Sect. 2, that, although non-regular, if a smooth function \(\psi\) has a minimizer at \(C_{1,4}\), its gradient \(\nabla \psi (C_{1,4})\) is necessarily null; so that \(C_{1,4}\) is a KKT point of the minimization of \(\psi\) subject to \(\varphi \le 0\).
References
Aarts, E., Lenstra, J. K., (eds.): Local search in combinatorial optimization, Princeton University Press, (2003)
Amaral, V.A., Andreani, R., Birgin, E.G., Marcondes, D.S., Martínez, J.M.: On complexity and convergence of high-order coordinate descent algorithms for smooth nonconvex box-constrained minimization. J. Glob. Optim. https://doi.org/10.1007/s10898-022-0.1168-6 (to appear)
Applegate, D. L., Bixby, R. E., Chvátal, V., Cook, W. J.: The traveling salesman problem: a computational study, Princeton University Press, (2006)
Birgin, E.G., Gardenghi, J.L., Martínez, J.M., Santos, S.A., Toint, Ph.L.: Worst-case evaluation complexity for unconstrained nonlinear optimization using high-order regularized models. Mathematical Programming 163, 359–368 (2017)
Birgin, E.G., Martínez, J.M.: On regularization and active-set methods with complexity for constrained optimization. SIAM Journal on Optimization 28, 1367–1395 (2018)
Birgin, E.G., Martínez, J.M.: A Newton-like method with mixed factorizations and cubic regularization for unconstrained minimization. Computational Optimization and Applications 73, 707–753 (2019)
Bonettini, S., Prato, M., Begegoldi, S.: A cyclic block coordinate descent method with generalized gradient projections. Applied Mathematics and Computation 286, 288–300 (2016)
Gendreau, M., Hertz, A., Laporte, G.: New insertion and post optimization procedures for the traveling salesman problem. Operations Research 40, 1086–1094 (1992)
Nocedal, J., Wright, S.J.: Numerical Optimization. Springer, New York, NY (2006)
Powell, M.J.D.: On search directions for minimization algorithms. Mathematical Programming 4, 193–201 (1973)
Wright, S.J.: Coordinate descent methods. Mathematical Programming 151, 3–34 (2015)
Funding
This work was supported by FAPESP (Grants 2013/07375-0, 2016/01860-1, and 2018/24293-0) and CNPq (Grants 302538/2019-4 and 302682/2019-8)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Birgin, E.G., Martínez, J.M. Block coordinate descent for smooth nonconvex constrained minimization. Comput Optim Appl 83, 1–27 (2022). https://doi.org/10.1007/s10589-022-00389-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10589-022-00389-5