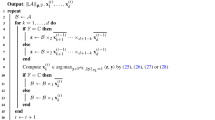1 Introduction

The spectral p-norm of a tensor generalizes the spectral p-norm of a matrix. It can be defined by the \(L_p\)-sphere constrained multilinear form optimization problem:

$$\begin{aligned} \Vert {\mathcal {T}}\Vert _{p_\sigma } = \max \left\{ {\mathcal {T}}({\varvec{x}}^1,{\varvec{x}}^2,\dots ,{\varvec{x}}^d): \Vert {\varvec{x}}^k\Vert _p=1,\, {\varvec{x}}^k\in {\mathbb {R}}^{n_k},\, k=1,2,\dots ,d \right\} , \end{aligned}$$

where \(\Vert {\mathcal {T}}\Vert _{p_\sigma }\) denotes the spectral p-norm of a given tensor \({\mathcal {T}}=\left( t_{i_1i_2\dots i_d}\right) \in {\mathbb {R}}^{n_1\times n_2\times \dots \times n_d}\),

$$\begin{aligned} {\mathcal {T}}({\varvec{x}}^1,{\varvec{x}}^2,\dots ,{\varvec{x}}^d) = \sum _{i_1=1}^{n_1}\sum _{i_2=1}^{n_2}\dots \sum _{i_d=1}^{n_d} t_{i_1i_2\dots i_d} x^1_{i_1}x^2_{i_2}\dots x^d_{i_d} \end{aligned}$$
(1)

is a multilinear form of \(({\varvec{x}}^1,{\varvec{x}}^2,\dots ,{\varvec{x}}^d)\), and \(\Vert \varvec{\cdot }\Vert _p\) denotes the \(L_p\)-norm of a vector for \(1\le p\le \infty\). When the order of the tensor \({\mathcal {T}}\) is two, the problem is reduced to the spectral p-norm of a matrix, and in particular when \(p=2\), to the spectral norm or the largest singular value of a matrix. The spectral p-norm of a tensor was proposed by Lim [18] in terms of singular values of a tensor, and is closely related to the largest Z-eigenvalue (for the case \(p=2\)) of a tensor proposed by Qi [24].

The matrix spectral p-norm is evidently important in many branches of mathematics as well as in various practical applications; see e.g., [6, 11]. The complexity and approximation methods of the matrix spectral p-norm were studied extensively [1, 21, 27], and they have particular applications in robust optimization [27]. When \(p=1,2\), the matrix spectral p-norm can be computed easily, and when \(2<p\le \infty\), computing the matrix spectral p-norm is NP-hard, while it remains unknown for the rest of p. The tensor spectral p-norm was studied mainly in approximation algorithms of polynomial optimization [15]. When the order of a tensor is larger than two, computing the tensor spectral norm (\(p=2\)) is already NP-hard proved by He et al. [8] (see also [10]), a sharp contrast to the case of matrices. NP-hardness to compute the tensor spectral p-norm was also established when \(2<p\le \infty\) by Hou and So [12]. Various approximation bounds of the tensor spectral p-norm were established in the literature [7,8,9, 12, 26]. Nikiforov [23] studied the tensor spectral p-norm using combinatorial methods and proposed several bounds. Li and Zhao [17] recently studied a more general tensor spectral p-norm and provided upper bounds via norm compression tensors.

The dual norm to the spectral p-norm of a tensor \({\mathcal {T}}\), called the nuclear p-norm, is defined as \(\Vert {\mathcal {T}}\Vert _{p_*}=\max _{\Vert {\mathcal {X}}\Vert _{p_\sigma }\le 1}\langle {\mathcal {T}},{\mathcal {X}}\rangle\). In the case of matrices and \(p=2\), it is reduced to the nuclear norm of a matrix, which is equal to the sum of all the singular values of a matrix. The matrix nuclear norm was used widely as a convex envelope of the matrix rank for many rank minimization problems, such as matrix completion [2]. Friedland and Lim [4] studied the tensor nuclear p-norm systematically, and showed that computing the tensor nuclear norm (\(p=2)\) is NP-hard when the order of the tensor is larger than two. They also proposed simple lower and upper bounds of the tensor spectral norm and nuclear norm. The study on the tensor nuclear p-norm has been mainly focused on the case \(p=2\), such as tensor completion [5, 20, 30]. Derksen [3] discussed the nuclear norm of various tensors based on orthogonality. Nie [22] studied symmetric tensor nuclear norms. Extremal properties of the tensor spectral norm and nuclear norm were studied in [16].

Most of the methods to tackle the tensor spectral p-norm and nuclear p-norm in the literature have been heavily relying on matrix unfoldings, no matter in theory such as approximation methods [15] and in practice such as tensor completion [5]. Hu [13] established the relation of the tensor nuclear norm to the nuclear norms of its matrix unfoldings. Wang et al. [29] systematically studied the tensor spectral p-norm via various matrix unfoldings and tensor unfoldings. Li [14] proposed a novel approach to study the tensor spectral norm and nuclear norm via tensor partitions, a concept generalizing block tensors by Ragnarsson and Van Loan [25]. Some neat bounds of the tensor spectral norm (respectively, nuclear norm) via the spectral norms (respectively, nuclear norms) of subtensors in any regular partition were proposed, and a conjecture [14, Conjecture 3.5] on the bounds in any tensor partition was proposed.

In this paper, we systematically study the tensor spectral p-norm and nuclear p-norm via the partition approach in [14]. We prove that for the most general partition called arbitrary partition, the bounds of the tensor spectral p-norm and nuclear p-norm via subtensors can be established for any \(1\le p\le \infty\). It generalizes and answers affirmatively the Li’s conjecture, which is the case \(p=2\) for a tensor partition. The novelty of the proof lies in establishing an index system to describe subtensors in an arbitrary partition. Based on these, we study the relations of the spectral p-norm of a tensor, the spectral p-norms of matrix unfoldings of the tensor, and the bounds via the spectral p-norms of matrix slices of the tensor. The same relation is studied for the tensor nuclear p-norm. Various bounds of these tensor norms in the literature can be derived from our results.

This paper is organized as follows. We start with the preparation of various notations, definitions and properties of tensor norms and tensor partitions in Sect. 2. In Sect. 3, we present our main result on bounding the tensor spectral p-norm and nuclear p-norm via partitioned subtensors. Section 4 is devoted to the discussion and theoretical applications, particularly on the relations among the tensor norms, the norms of matrix unfoldings, and the norms via matrix slices.

2 Preparation

Throughout this paper, we uniformly use the lower case letters (e.g., x), the boldface lower case letters (e.g., \({\varvec{x}}=\left( x_i\right)\)), the capital letters (e.g., \(X=\left( x_{ij}\right)\)), and the calligraphic letters (e.g., \({\mathcal {X}}=\left( x_{i_1i_2\dots i_d}\right)\)) to denote scalars, vectors, matrices, and higher order (order three or more) tensors, respectively. Denote \({\mathbb {R}}^{n_1\times n_2\times \dots \times n_d}\) to be the space of dth order real tensors of dimension \(n_1\times n_2\times \dots \times n_d\). The same notations apply for a vector space and a matrix space when \(d=1\) and \(d=2\), respectively. Denote \({\mathbb {N}}\) to be the set of positive integers.

Given a dth order tensor space \({\mathbb {R}}^{n_1\times n_2\times \dots \times n_d}\), we denote \({\mathbb {I}}^k:=\left\{ 1,2,\dots ,n_k\right\}\) to be the index set of mode-k for \(k=1,2,\dots ,d\). Trivially, \({\mathbb {I}}^1\times {\mathbb {I}}^2\times \dots \times {\mathbb {I}}^d\) becomes the index set of the entries of a tensor in the tensor space. The Frobenius inner product of two tensors \({\mathcal {U}},{\mathcal {V}}\in {\mathbb {R}}^{n_1\times n_2\times \dots \times n_d}\) is defined as:

$$\begin{aligned} \langle {\mathcal {U}},{\mathcal {V}}\rangle :=\sum _{i_1=1}^{n_1}\sum _{i_2=1}^{n_2} \dots \sum _{i_d=1}^{n_d} u_{i_1i_2\dots i_d} v_{i_1i_2\dots i_d}. \end{aligned}$$

Its induced Frobenius norm is naturally defined as \(\Vert {\mathcal {T}}\Vert _2:=\sqrt{\langle {\mathcal {T}},{\mathcal {T}}\rangle }\). When \(d=1\), the Frobenius norm is reduced to the Euclidean norm of a vector. In a similar vein, we may define the \(L_p\)-norm of a tensor (also known as the Hölder p-norm) for \(1\le p\le \infty\) to looking at a tensor as a vector, as follows:

$$\begin{aligned} \Vert {\mathcal {T}}\Vert _p=\left( \sum _{i_1=1}^{n_1}\sum _{i_2=1}^{n_2} \dots \sum _{i_d=1}^{n_d} |t_{i_1i_2\dots i_d}|^p\right) ^{\frac{1}{p}}. \end{aligned}$$

A rank-one tensor, also called a simple tensor, is a tensor that can be written as outer products of vectors, i.e., \({\mathcal {T}}={\varvec{x}}^1\otimes {\varvec{x}}^2\otimes \dots \otimes {\varvec{x}}^d\) where \({\varvec{x}}^k\in {\mathbb {R}}^{n_k}\) for \(k=1,2,\dots ,d\). It can be equivalently represented by the entries as:

$$\begin{aligned} t_{i_1i_2\dots i_d}=\prod _{k=1}^d x^k_{i_k} \quad \forall \,\left( i_1,i_2,\dots ,i_d\right) \in {\mathbb {I}}^1\times {\mathbb {I}}^2 \times \dots \times {\mathbb {I}}^d. \end{aligned}$$
(2)

Here is a property of the \(L_p\)-norm of a rank-one tensor.

Proposition 2.1

If a tensor\({\mathcal {T}}\in {\mathbb {R}}^{n_1\times n_2\times \dots \times n_d}\)is rank-one, say\({\mathcal {T}}={\varvec{x}}^1\otimes {\varvec{x}}^2\otimes \dots \otimes {\varvec{x}}^d\), then\(\Vert {\mathcal {T}}\Vert _p=\prod _{k=1}^d\Vert {\varvec{x}}^d\Vert _p\)for any\(1\le p\le \infty\).

Proof

According to (2), we have

$$\begin{aligned} \Vert {\mathcal {T}}\Vert _p = \left( \sum _{i_1=1}^{n_1}\sum _{i_2=1}^{n_2} \dots \sum _{i_d=1}^{n_d} \left| \prod _{k=1}^d x^k_{i_k}\right| ^p\right) ^{\frac{1}{p}} = \left( \prod _{k=1}^d \left( \sum _{i_k=1}^{n_k}\left| x^k_{i_k}\right| ^p\right) \right) ^{\frac{1}{p}} = \prod _{k=1}^d\Vert {\varvec{x}}^k\Vert _p. \end{aligned}$$

\(\square\)

2.1 The spectral p-norm and nuclear p-norm

Let us formally define the tensor spectral p-norm and its dual norm.

Definition 2.2

For a given tensor \({\mathcal {T}}\in {\mathbb {R}}^{n_1\times n_2\times \dots \times n_d}\) and \(1\le p\le \infty\), the spectral p-norm of \({\mathcal {T}}\), denoted by \(\Vert {\mathcal {T}}\Vert _{p_\sigma }\), is defined as

$$\begin{aligned} \Vert {\mathcal {T}}\Vert _{p_\sigma }:=\max \left\{ \left\langle {\mathcal {T}}, {\varvec{x}}^1\otimes {\varvec{x}}^2\otimes \dots \otimes {\varvec{x}}^d \right\rangle : \Vert {\varvec{x}}^k\Vert _p=1, \, k=1,2,\dots ,d\right\} . \end{aligned}$$
(3)

Essentially, \(\Vert {\mathcal {T}}\Vert _{p_\sigma }\) is the maximal value of the Frobenius inner product between \({\mathcal {T}}\) and a rank-one tensor whose \(L_p\)-norm is one, according to Proposition 2.1. We remark that \(\left\langle {\mathcal {T}}, {\varvec{x}}^1\otimes {\varvec{x}}^2\otimes \dots \otimes {\varvec{x}}^d \right\rangle\) in (3) is exactly the multilinear form \({\mathcal {T}}({\varvec{x}}^1,{\varvec{x}}^2,\dots ,{\varvec{x}}^d)\) defined in (1). Hence, as mentioned in Sect. 1, the tensor spectral p-norm is more commonly known as the \(L_p\)-sphere constrained multilinear form optimization problem in the optimization community. When \(p=2\), the tensor spectral p-norm is often called the tensor spectral norm, and is also known to be the largest singular value of the tensor [18].

Definition 2.3

For a given tensor \({\mathcal {T}}\in {\mathbb {R}}^{n_1\times n_2\times \dots \times n_d}\) and \(1\le p\le \infty\), the nuclear p-norm of \({\mathcal {T}}\), denoted by \(\Vert {\mathcal {T}}\Vert _{p_*}\), is defined as

$$\begin{aligned} \Vert {\mathcal {T}}\Vert _{p_*}:=\min \left\{ \sum _{i=1}^r|\lambda _i| : {\mathcal {T}}=\sum _{i=1}^r\lambda _i {\varvec{x}}^1_i\otimes {\varvec{x}}^2_i\otimes \dots \otimes {\varvec{x}}^d_i, \Vert {\varvec{x}}^k_i\Vert _p=1\hbox { for all}\ k\hbox { and }i, \, r\in {\mathbb {N}}\right\} . \end{aligned}$$
(4)

The decomposition of \({\mathcal {T}}\) into a sum of rank-one tensors, such as that in (4), is called a rank-one decomposition of \({\mathcal {T}}\). Therefore, the tensor nuclear p-norm is the minimum of the sum of the \(L_p\)-norms of rank-one tensors in any rank-one decomposition. A rank-one decomposition of \({\mathcal {T}}\) that attains \(\Vert {\mathcal {T}}\Vert _{p_*}\) is called a nuclear p-decomposition of \({\mathcal {T}}\), similar to the nuclear decomposition of a tensor for \(p=2\) discussed in [4]. When \(p=2\), the tensor nuclear p-norm is commonly known as the tensor nuclear norm. The tensor nuclear norm is the convex envelope of the tensor rank and is widely used in tensor completion [30].

We provide some basic facts of the tensor spectral p-norm and nuclear p-norm. The proof is essentially based on the Hölder’s inequality.

Proposition 2.4

For any\(1\le p,q\le \infty\)with\(\frac{1}{p}+\frac{1}{q}=1\), we have the followings:

  • For a scalar\(t\in {\mathbb {R}}\), \(\Vert t\Vert _{p_\sigma }=\Vert t\Vert _{p_*}=|t|\);

  • For a vector\({\varvec{t}}\in {\mathbb {R}}^n\), \(\Vert {\varvec{t}}\Vert _{p_\sigma }=\Vert {\varvec{t}}\Vert _q\)and\(\Vert {\varvec{t}}\Vert _{p_*}=\Vert {\varvec{t}}\Vert _p\);

  • For a rank-one tensor\({\mathcal {T}}\), \(\Vert {\mathcal {T}}\Vert _{p_\sigma }=\Vert {\mathcal {T}}\Vert _q\)and\(\Vert {\mathcal {T}}\Vert _{p_*}=\Vert {\mathcal {T}}\Vert _p\).

The tensor nuclear p-norm is the dual norm to the tensor spectral p-norm, and vice versa, for any \(1\le p\le \infty\).

Lemma 2.5

For given tensors\({\mathcal {T}}\)and\({\mathcal {Z}}\)in a same tensor space and\(1\le p\le \infty\), it follows that

$$\begin{aligned}\langle {\mathcal {T}},{\mathcal {Z}}\rangle \le \Vert {\mathcal {T}}\Vert _{p_\sigma } \Vert {\mathcal {Z}}\Vert _{p_*},\end{aligned}$$

and further

$$\begin{aligned} \Vert {\mathcal {T}}\Vert _{p_\sigma }&=\max _{\Vert {\mathcal {Z}}\Vert _{p_*}\le 1}\langle {\mathcal {T}},{\mathcal {Z}}\rangle , \nonumber \\ \Vert {\mathcal {T}}\Vert _{p_*}&=\max _{\Vert {\mathcal {Z}}\Vert _{p_\sigma }\le 1}\langle {\mathcal {T}},{\mathcal {Z}}\rangle . \end{aligned}$$
(5)

Proof

Let \({\mathcal {Z}}=\sum _{i=1}^r\lambda _i {\varvec{x}}^1_i\otimes {\varvec{x}}^2_i\otimes \dots \otimes {\varvec{x}}^d_i\) with \(\Vert {\varvec{x}}^k_i\Vert _p=1\) for all k and i with \(\Vert {\mathcal {Z}}\Vert _{p_*}=\sum _{i=1}^r|\lambda _i|\), i.e., a nuclear p-decomposition of \({\mathcal {Z}}\). By Definition 2.2,

$$\begin{aligned} \langle {\mathcal {T}}, {\varvec{x}}^1_i\otimes {\varvec{x}}^2_i\otimes \dots \otimes {\varvec{x}}^d_i\rangle \le \Vert {\mathcal {T}}\Vert _{p_\sigma } \quad \forall \,i=1,2,\dots ,r, \end{aligned}$$

which leads to

$$\begin{aligned} \langle {\mathcal {T}},{\mathcal {Z}}\rangle = \sum _{i=1}^r \lambda _i \langle {\mathcal {T}}, {\varvec{x}}^1_i\otimes {\varvec{x}}^2_i\otimes \dots \otimes {\varvec{x}}^d_i\rangle \le \sum _{i=1}^r |\lambda _i| \cdot \Vert {\mathcal {T}}\Vert _{p_\sigma } = \Vert {\mathcal {T}}\Vert _{p_\sigma } \Vert {\mathcal {Z}}\Vert _{p_*}. \end{aligned}$$

By choosing \(\Vert {\mathcal {Z}}\Vert _{p_*}\le 1\), we have

$$\begin{aligned} \max _{\Vert {\mathcal {Z}}\Vert _{p_*}\le 1} \langle {\mathcal {T}},{\mathcal {Z}}\rangle \le \max _{\Vert {\mathcal {Z}}\Vert _{p_*}\le 1} \Vert {\mathcal {T}}\Vert _{p_\sigma } \Vert {\mathcal {Z}}\Vert _{p_*} = \Vert {\mathcal {T}}\Vert _{p_\sigma }. \end{aligned}$$

On the other hand, let \(\Vert {\mathcal {T}}\Vert _{p_\sigma }=\langle {\mathcal {T}}, {\varvec{y}}^1\otimes {\varvec{y}}^2\otimes \dots \otimes {\varvec{y}}^d \rangle\) with \(\Vert {\varvec{y}}^k\Vert _p=1\) for all k. By Proposition 2.4, we have

$$\begin{aligned} \Vert {\varvec{y}}^1\otimes {\varvec{y}}^2\otimes \dots \otimes {\varvec{y}}^d\Vert _{p_*}=\Vert {\varvec{y}}^1\otimes {\varvec{y}}^2\otimes \dots \otimes {\varvec{y}}^d\Vert _p =\prod _{k=1}^d\Vert {\varvec{y}}^k\Vert _p=1, \end{aligned}$$

which leads to

$$\begin{aligned} \max _{\Vert {\mathcal {Z}}\Vert _{p_*}\le 1} \langle {\mathcal {T}},{\mathcal {Z}}\rangle \ge \langle {\mathcal {T}}, {\varvec{y}}^1\otimes {\varvec{y}}^2\otimes \dots \otimes {\varvec{y}}^d \rangle = \Vert {\mathcal {T}}\Vert _{p_\sigma }. \end{aligned}$$

Therefore, \(\max _{\Vert {\mathcal {Z}}\Vert _{p_*}\le 1} \langle {\mathcal {T}},{\mathcal {Z}}\rangle = \Vert {\mathcal {T}}\Vert _{p_\sigma }\) and so as to the other dual norm equality. \(\square\)

We remark that the proof of Lemma 2.5 for \(p=2\) can be found in [3, 19]. When \(d=2\), the tensor spectral p-norm and nuclear p-norm are reduced to the matrix spectral p-norm and nuclear p-norm, respectively. When \(d=1\), a vector, its spectral p-norm is the \(L_q\)-norm where \(\frac{1}{p}+\frac{1}{q}=1\) and its nuclear p-norm is the \(L_p\)-norm, as mentioned in Proposition 2.4. Two extreme cases of these norms worth mentioning, and they are the only known easy cases to compute.

Proposition 2.6

For any tensor\({\mathcal {T}}\), it follows that\(\Vert {\mathcal {T}}\Vert _{1_\sigma }=\Vert {\mathcal {T}}\Vert _\infty\)and\(\Vert {\mathcal {T}}\Vert _{1_*}=\Vert {\mathcal {T}}\Vert _1\).

Proof

Let \(|t_{s_1s_2\dots s_d}|=\max _{i_k\in {\mathbb {I}}^k,\,k=1,2,\dots ,d}|t_{i_1i_2\dots i_d}|=\Vert {\mathcal {T}}\Vert _\infty\). For any \({\varvec{x}}^k\in {\mathbb {R}}^{n_k}\) with \(\Vert {\varvec{x}}^k\Vert _1=1\) for \(k=1,2,\dots ,d\),

$$\begin{aligned} \left\langle {\mathcal {T}}, {\varvec{x}}^1\otimes {\varvec{x}}^2\otimes \dots \otimes {\varvec{x}}^d \right\rangle&= \sum _{i_1=1}^{n_1}\sum _{i_2=1}^{n_2}\dots \sum _{i_d=1}^{n_d} t_{i_1i_2\dots i_d} x^1_{i_1}x^2_{i_2}\dots x^d_{i_d} \\&\le \sum _{i_1=1}^{n_1}\sum _{i_2=1}^{n_2}\dots \sum _{i_d=1}^{n_d} |t_{s_1s_2\dots s_d}| \cdot |x^1_{i_1}x^2_{i_2}\dots x^d_{i_d}| \\&= |t_{s_1s_2\dots s_d}| \prod _{k=1}^n \Vert {\varvec{x}}^k\Vert _1 \\&= |t_{s_1s_2\dots s_d}|, \end{aligned}$$

implying that \(\Vert {\mathcal {T}}\Vert _{1_\sigma }\le \Vert {\mathcal {T}}\Vert _\infty\). On the other hand, denote \({\varvec{e}}^i\) to be the vector whose ith entry is one and others are zeros. Clearly \(\Vert {\varvec{e}}^i\Vert _1=1\), and we have

$$\begin{aligned} \left\langle {\mathcal {T}}, {\varvec{e}}^{s_1}\otimes {\varvec{e}}^{s_2}\otimes \dots \otimes {\varvec{e}}^{s_d} \right\rangle = t_{s_1s_2\dots s_d}, \end{aligned}$$

implying that \(\Vert {\mathcal {T}}\Vert _{1_\sigma }\ge |t_{s_1s_2\dots s_d}| =\Vert {\mathcal {T}}\Vert _\infty\). Therefore, \(\Vert {\mathcal {T}}\Vert _{1_\sigma }=\Vert {\mathcal {T}}\Vert _\infty\), and the other identity follows since the dual norm of the tensor \(L_1\)-norm is the tensor \(L_\infty\)-norm. \(\square\)

2.2 Tensor partitions

A matrix can be partitioned into submatrices, the same can be applied to a tensor. One important class of tensor partitions, block tensors, was proposed and studied in [25, 28]. It is a straightforward generalization of block matrices. Li [14] proposed three types of partitions for tensors, namely, modal partitions (an alternative name for block tensors), regular partitions, and tensor partitions, with the latter generalizing the former. Some neat bounds on the tensor spectral norm and nuclear norm based on regular partitions were proposed in [14]. The proofs heavily relied on the recursive structure in defining regular partitions. Since we are extending the results to a more general class of partitions than tensor partitions, we only discuss the definition of tensor partitions and refer modal partitions and regular partitions to [14].

Before presenting the partition concepts, we first discuss notations to describe subtensors of a tensor. It is also an essential step to prove our main bounds to be established in Sect. 3. Suppose that \({\mathcal {T}}_j\) is a subtensor of a tensor \({\mathcal {T}}\in {\mathbb {R}}^{n_1\times n_2\times \dots \times n_d}\). We denote the set of its mode-k indices in the original tensor \({\mathcal {T}}\) to be \({\mathbb {I}}_j^k\) for \(k=1,2,\dots ,d\). We then let

$$\begin{aligned} {\mathcal {T}}_j={\mathcal {T}}\left( {\mathbb {I}}_j^1, {\mathbb {I}}_j^2, \dots , {\mathbb {I}}_j^d\right) \text{ where } {\mathbb {I}}_j^k\subset {\mathbb {I}}^k \text{ for } k=1,2,\dots ,d. \end{aligned}$$

Specifically, \({\mathcal {T}}_j\) is a subtensor of \({\mathcal {T}}\) by keeping only the indices in \({\mathbb {I}}_j^k\) of mode-k for \(k=1,2,\dots ,d\). Alternatively, \({\mathcal {T}}_j\) is a subtensor by deleting all the indices in \({\mathbb {I}}^k/{\mathbb {I}}_j^k\) of mode-k for \(k=1,2,\dots ,d\) from the original tensor \({\mathcal {T}}\). The dimension of the subtensor \({\mathcal {T}}_j\) is \(|{\mathbb {I}}_j^1|\times |{\mathbb {I}}_j^2|\times \dots \times |{\mathbb {I}}_j^d|\). In our analysis, we do not relabel the indices of some mode of \({\mathcal {T}}_j\), say \({\mathbb {I}}_j^k\), to \(\{1,2,\dots ,|{\mathbb {I}}_j^k|\}\), but keep its original indices in \({\mathcal {T}}\).

Definition 2.7

[14, Definition 2.4] A partition \(\left\{ {\mathcal {T}}_1,{\mathcal {T}}_2,\dots ,{\mathcal {T}}_m\right\}\) is called a tensor partition of a tensor \({\mathcal {T}}\), if

  • every \({\mathcal {T}}_j~\left( j=1,2,\dots ,m\right)\) can be written as \({\mathcal {T}}\left( {\mathbb {I}}_j^1, {\mathbb {I}}_j^2, \dots , {\mathbb {I}}_j^d\right)\) where the indices of every \({\mathbb {I}}_j^k\subset {\mathbb {I}}^k~\left( k=1,2,\dots ,d\right)\) are consecutive,

  • every pair \(\left\{ {\mathcal {T}}_i,{\mathcal {T}}_j\right\}\) with \(i\ne j\) has no common entry of \({\mathcal {T}}\), and

  • every entry of \({\mathcal {T}}\) belongs to one of \(\left\{ {\mathcal {T}}_1,{\mathcal {T}}_2,\dots ,{\mathcal {T}}_m\right\}\).

We remark that as a tensor partition, every subtensor \({\mathcal {T}}_j\) must be a whole block (not disconnected) from the original tensor \({\mathcal {T}}\). The following observation is straightforward from Definition 2.7.

Proposition 2.8

If\(\left\{ {\mathcal {T}}_1,{\mathcal {T}}_2,\dots ,{\mathcal {T}}_m\right\}\)is a tensor partition ofa tensor\({\mathcal {T}}\)where

$$\begin{aligned} {\mathcal {T}}_j={\mathcal {T}}\left( {\mathbb {I}}_j^1, {\mathbb {I}}_j^2, \dots , {\mathbb {I}}_j^d\right) \quad \forall \,j=1,2,\dots ,m, \end{aligned}$$

then\(\left\{ {\mathbb {I}}_j^1 \times {\mathbb {I}}_j^2 \times \dots \times {\mathbb {I}}_j^d: j=1,2,\dots ,m\right\}\)is a partition of\({\mathbb {I}}^1 \times {\mathbb {I}}^2 \times \dots \times {\mathbb {I}}^d\), the index set of\({\mathcal {T}}\).

In a similar way, we denote \({\varvec{x}}({\mathbb {I}}_j^k)\in {\mathbb {R}}^{|{\mathbb {I}}_j^k|}\) to be the vector by keeping only the entries of \({\varvec{x}}\) with indices in \({\mathbb {I}}_j^k\), or the vector by deleting the entries of \({\varvec{x}}\) whose indices are not in \({\mathbb {I}}_j^k\). Again, in our analysis, we do not relabel these indices to \(\{1,2,\dots ,|{\mathbb {I}}_j^k|\}\).

We remark that Proposition 2.8 indeed implies a more general partition concept than the tensor partition in Definition 2.7. We may further drop the requirement of the indices of \({\mathbb {I}}_j^k\) to be consecutive for \({\mathcal {T}}_j\). In this case, \({\mathcal {T}}_j\) may consist several disconnected pieces by viewing from the original tensor \({\mathcal {T}}\) but can be put together to form a tensor by deleting empty entries from \({\mathcal {T}}\) (see Example 2.10). Although one can relabel some mode-k indices (similar operations to swapping rows or columns in a matrix) to make one of \({\mathcal {T}}_j\)’s to be a tensor with consecutive indices in every mode, it may break other \({\mathcal {T}}_j\)’s into disconnected pieces. Hence, one can define a more general partition concept that allows disconnections.

Definition 2.9

A partition \(\left\{ {\mathcal {T}}_1,{\mathcal {T}}_2,\dots ,{\mathcal {T}}_m\right\}\) where

$$\begin{aligned} {\mathcal {T}}_j={\mathcal {T}}\left( {\mathbb {I}}_j^1, {\mathbb {I}}_j^2, \dots , {\mathbb {I}}_j^d\right) \quad \forall \,j=1,2,\dots ,m \end{aligned}$$

and \({\mathbb {I}}_j^k\subset {\mathbb {I}}^k\) for \(k=1,2,\dots ,d\) and \(j=1,2,\dots ,m\) is called an arbitrary partition of a tensor \({\mathcal {T}}\in {\mathbb {R}}^{n_1\times n_2\times \dots \times n_d}\) if \(\left\{ {\mathbb {I}}_j^1 \times {\mathbb {I}}_j^2 \times \dots \times {\mathbb {I}}_j^d: j=1,2,\dots ,m\right\}\) is a partition of \({\mathbb {I}}^1 \times {\mathbb {I}}^2 \times \dots \times {\mathbb {I}}^d\).

Arbitrary partitions is the most general case of partitioning a tensor. The following example indicates the key difference between a tensor partition and an arbitrary partition for a matrix. Obviously, arbitrary partitions can be far more complicated than tensor partitions for higher order tensors.

Example 2.10

Let \(M\in {\mathbb {R}}^{4\times 6}\) be a matrix shown as \(4\times 6\) blocks in Fig. 1.

  • For (a), \(\left\{ A,B,C,D,E,F\right\}\) is a tensor partition (a special arbitrary partition) of M with \(A,B,C,D\in {\mathbb {R}}^{2\times 2}\) and \(E,F\in {\mathbb {R}}^{1\times 4}\).

  • For (b), \(\left\{ U,V,W,X,Y,Z\right\}\) is an arbitrary partition (but not a tensor partition) of M with \(U,V,W\in {\mathbb {R}}^{2\times 2}\) and \(X,Y,Z\in {\mathbb {R}}^{1\times 4}\). Here \(V=\genfrac(){0.0pt}0{V_1}{V_2}\), \(W=\genfrac(){0.0pt}0{W_1}{W_2}\), and \(Y=(Y_1,Y_2)\) are disconnected in M.

Fig. 1
figure 1

Tensor partition and arbitrary partition of a second order tensor (matrix)

Full size image

In particular, there is no way for a tensor partition of a \(4\times 6\) matrix consisting of exactly three \(2\times 2\) matrices and three \(1\times 4\) matrices. However, an arbitrary partition can make it, such as the partition in the right subfigure of Fig. 1.

Finally in this section, we remark that some \({\mathcal {T}}_j\) (either connected or disconnected) in an arbitrary partition of a tensor may not have the same order of the original tensor \({\mathcal {T}}\). If some \({\mathbb {I}}_j^k\) contains only one index, this causes the disappearance of mode-k and reduces the order of \({\mathcal {T}}_j\) by one. However, we still treat this \({\mathcal {T}}_j\) as a dth order tensor by keeping the dimension of mode-k to be one. For instance, we can always treat a scalar as a one-dimensional vector, or a one-by-one matrix.

3 Bounds of the tensor norms

With the establishment of the index system to describe subtensors in an arbitrary partition, we are now in a better position to present and prove the main results in this paper, bounding the spectral p-norm and the nuclear p-norm of a tensor via the spectral p-norms and the nuclear p-norms of subtensors in an arbitrary partition.

Theorem 3.1

If\(\left\{ {\mathcal {T}}_1,{\mathcal {T}}_2,\dots ,{\mathcal {T}}_m\right\}\)is an arbitrarypartition of a tensor\({\mathcal {T}}\)and\(1\le p,q\le \infty\)with\(\frac{1}{p}+\frac{1}{q}=1\), then

$$\begin{aligned} \left\| \left( \Vert {\mathcal {T}}_1\Vert _{p_\sigma },\Vert {\mathcal {T}}_2\Vert _{p_\sigma },\dots ,\Vert {\mathcal {T}}_m\Vert _{p_\sigma }\right) \right\| _\infty&\le \Vert {\mathcal {T}}\Vert _{p_\sigma } \le \left\| \left( \Vert {\mathcal {T}}_1\Vert _{p_\sigma },\Vert {\mathcal {T}}_2\Vert _{p_\sigma },\dots ,\Vert {\mathcal {T}}_m\Vert _{p_\sigma }\right) \right\| _q, \end{aligned}$$
(6)
$$\begin{aligned} \left\| \left( \Vert {\mathcal {T}}_1\Vert _{p_*},\Vert {\mathcal {T}}_2\Vert _{p_*},\dots ,\Vert {\mathcal {T}}_m\Vert _{p_*}\right) \right\| _p&\le \Vert {\mathcal {T}}\Vert _{p_*} \le \left\| \left( \Vert {\mathcal {T}}_1\Vert _{p_*},\Vert {\mathcal {T}}_2\Vert _{p_*},\dots ,\Vert {\mathcal {T}}_m\Vert _{p_*}\right) \right\| _1. \end{aligned}$$
(7)

Proof

For an arbitrary partition \(\left\{ {\mathcal {T}}_1,{\mathcal {T}}_2,\dots ,{\mathcal {T}}_m\right\}\) of \({\mathcal {T}}\), let \({\mathcal {T}}_j={\mathcal {T}}\left( {\mathbb {I}}_j^1, {\mathbb {I}}_j^2, \dots , {\mathbb {I}}_j^d\right)\), where \({\mathbb {I}}_j^k\subset {\mathbb {I}}^k\) for \(k=1,2,\dots ,d\) and \(j=1,2,\dots ,m\). The whole proof is divided into four steps, each one showing one bound in (6) and (7).

  1. (1)

    The lower bound of \(\Vert {\mathcal {T}}\Vert _{p_\sigma }\) in (6).

    For any given \({\mathcal {T}}_j\), we let \({\varvec{y}}^k\in {\mathbb {R}}^{|{\mathbb {I}}_j^k|}\) with \(\Vert {\varvec{y}}^k\Vert _p=1\) for \(k=1,2,\dots ,d\) be an optimal solution of \(\max \left\{ \left\langle {\mathcal {T}}_j, {\varvec{x}}^1\otimes {\varvec{x}}^2\otimes \dots \otimes {\varvec{x}}^d \right\rangle : \Vert {\varvec{x}}^k\Vert _p=1, \, k=1,2,\dots ,d\right\}\), i.e.,

    $$\begin{aligned} \Vert {\mathcal {T}}_j\Vert _{p_\sigma }=\left\langle {\mathcal {T}}_j,{\varvec{y}}^1\otimes {\varvec{y}}^2\otimes \dots \otimes {\varvec{y}}^d\right\rangle . \end{aligned}$$

    Instead of being \(\{1,2,\dots ,|{\mathbb {I}}^k_j|\}\), the indices of \({\varvec{y}}^k\) are kept as that of \({\mathbb {I}}^k_j\) for \(k=1,2,\dots ,d\). For every k, we define \({\varvec{x}}^k\in {\mathbb {R}}^{n_k}\) where

    $$\begin{aligned} x^k_i = \left\{ \begin{array}{ll} y^k_i &{} \quad i\in {\mathbb {I}}^k_j, \\ 0 &{} \quad i\in {\mathbb {I}}^k/{\mathbb {I}}^k_j. \end{array} \right. \end{aligned}$$

    Clearly we have \(\Vert {\varvec{x}}^k\Vert _p=\Vert {\varvec{y}}^k\Vert _p=1\). Therefore,

    $$\begin{aligned} \Vert {\mathcal {T}}_j\Vert _{p_\sigma }&= \left\langle {\mathcal {T}}_j,{\varvec{y}}^1\otimes {\varvec{y}}^2\otimes \dots \otimes {\varvec{y}}^d\right\rangle = \left\langle {\mathcal {T}},{\varvec{x}}^1\otimes {\varvec{x}}^2\otimes \dots \otimes {\varvec{x}}^d\right\rangle \le \Vert {\mathcal {T}}\Vert _{p_\sigma }, \end{aligned}$$

    proving that \(\max _{1\le j\le m} \Vert {\mathcal {T}}_j\Vert _{p_\sigma }\le \Vert {\mathcal {T}}\Vert _{p_\sigma }\).

  2. (2)

    The upper bound of \(\Vert {\mathcal {T}}\Vert _{p_\sigma }\) in (6).

    Let \({\varvec{x}}^k\in {\mathbb {R}}^{n_k}\) with \(\Vert {\varvec{x}}^k\Vert _p=1\) for \(k=1,2,\dots ,d\) be an optimal solution of (3), i.e.,

    $$\begin{aligned} \Vert {\mathcal {T}}\Vert _{p_\sigma }=\left\langle {\mathcal {T}},{\varvec{x}}^1\otimes {\varvec{x}}^2\otimes \dots \otimes {\varvec{x}}^d\right\rangle . \end{aligned}$$

    First, we observe that

    $$\begin{aligned} \left\langle {\mathcal {T}}_j,{\varvec{x}}^1({\mathbb {I}}_j^1)\otimes {\varvec{x}}^2({\mathbb {I}}_j^2)\otimes \dots \otimes {\varvec{x}}^d({\mathbb {I}}_j^d)\right\rangle \le \Vert {\mathcal {T}}_j\Vert _{p_\sigma }\prod _{k=1}^d \Vert {\varvec{x}}^k({\mathbb {I}}_j^k)\Vert _p. \end{aligned}$$
    (8)

    It is obvious that (8) holds trivially if one of \({\varvec{x}}^1({\mathbb {I}}_j^1),{\varvec{x}}^2({\mathbb {I}}_j^2),\dots , {\varvec{x}}^d({\mathbb {I}}_j^d)\) is a zero vector. Otherwise, we get

    $$\begin{aligned} \Vert {\mathcal {T}}_j\Vert _{p_\sigma }&\ge \left\langle {\mathcal {T}}_j, \frac{{\varvec{x}}^1({\mathbb {I}}_j^1)}{\Vert {\varvec{x}}^1({\mathbb {I}}_j^1)\Vert _p} \otimes \frac{{\varvec{x}}^2({\mathbb {I}}_j^2)}{\Vert {\varvec{x}}^2({\mathbb {I}}_j^2)\Vert _p} \otimes \dots \otimes \frac{{\varvec{x}}^d({\mathbb {I}}_j^d)}{\Vert {\varvec{x}}^d({\mathbb {I}}_j^d)\Vert _p} \right\rangle \\&= \frac{1}{\prod _{k=1}^d \Vert {\varvec{x}}^k({\mathbb {I}}_j^k)\Vert _p} \left\langle {\mathcal {T}}_j,{\varvec{x}}^1({\mathbb {I}}_j^1)\otimes {\varvec{x}}^2({\mathbb {I}}_j^2)\otimes \dots \otimes {\varvec{x}}^d({\mathbb {I}}_j^d)\right\rangle , \end{aligned}$$

    proving that (8) holds in general. Since \(\left\{ {\mathcal {T}}_1,{\mathcal {T}}_2,\dots ,{\mathcal {T}}_m\right\}\) is an arbitrary partition of \({\mathcal {T}}\), \(\left\{ {\mathbb {I}}_j^1 \times {\mathbb {I}}_j^2 \times \dots \times {\mathbb {I}}_j^d: j=1,2,\dots ,m\right\}\) is a partition of \(\left\{ {\mathbb {I}}^1 \times {\mathbb {I}}^2 \times \dots \times {\mathbb {I}}^d\right\}\). Therefore,

    $$\begin{aligned} \Vert {\mathcal {T}}\Vert _{p_\sigma }&=\left\langle {\mathcal {T}},{\varvec{x}}^1\otimes {\varvec{x}}^2\otimes \dots \otimes {\varvec{x}}^d\right\rangle \\&=\left\langle {\mathcal {T}}\left( {\mathbb {I}}^1, {\mathbb {I}}^2, \dots , {\mathbb {I}}^d\right) , \left( {\varvec{x}}^1\otimes {\varvec{x}}^2\otimes \dots \otimes {\varvec{x}}^d\right) \left( {\mathbb {I}}^1, {\mathbb {I}}^2, \dots , {\mathbb {I}}^d\right) \right\rangle \\&=\sum _{j=1}^m \left\langle {\mathcal {T}}\left( {\mathbb {I}}_j^1, {\mathbb {I}}_j^2, \dots , {\mathbb {I}}_j^d\right) , \left( {\varvec{x}}^1\otimes {\varvec{x}}^2\otimes \dots \otimes {\varvec{x}}^d\right) \left( {\mathbb {I}}_j^1, {\mathbb {I}}_j^2, \dots , {\mathbb {I}}_j^d\right) \right\rangle \\&= \sum _{j=1}^m \left\langle {\mathcal {T}}_j, {\varvec{x}}^1({\mathbb {I}}_j^1)\otimes {\varvec{x}}^2({\mathbb {I}}_j^2)\otimes \dots \otimes {\varvec{x}}^d({\mathbb {I}}_j^d)\right\rangle \\&\le \sum _{j=1}^m \left( \Vert {\mathcal {T}}_j\Vert _{p_\sigma }\prod _{k=1}^d \Vert {\varvec{x}}^k({\mathbb {I}}_j^k)\Vert _p\right) \\&\le \left( \sum _{j=1}^m{\Vert {\mathcal {T}}_j\Vert _{p_\sigma }}^q\right) ^{\frac{1}{q}} \left( \sum _{j=1}^m\left( \prod _{k=1}^d \Vert {\varvec{x}}^k({\mathbb {I}}_j^k)\Vert _p\right) ^p\right) ^{\frac{1}{p}} \\&=\left\| \left( \Vert {\mathcal {T}}_1\Vert _{p_\sigma },\Vert {\mathcal {T}}_2\Vert _{p_\sigma },\dots ,\Vert {\mathcal {T}}_m\Vert _{p_\sigma }\right) \right\| _q, \end{aligned}$$

    where the first inequality is due to (8), the second inequality follows from the Hölder’s inequality, and the last equality holds due to Proposition 2.1 and

    $$\begin{aligned} \sum _{j=1}^m \left( \prod _{k=1}^d \Vert {\varvec{x}}^k({\mathbb {I}}_j^k)\Vert _p\right) ^p&= \sum _{j=1}^m {\left\| {\varvec{x}}^1({\mathbb {I}}_j^1)\otimes {\varvec{x}}^2({\mathbb {I}}_j^2) \otimes \dots \otimes {\varvec{x}}^d({\mathbb {I}}_j^d)\right\| _p}^p \\&= \sum _{j=1}^m {\left\| \left( {\varvec{x}}^1\otimes {\varvec{x}}^2\otimes \dots \otimes {\varvec{x}}^d\right) \left( {\mathbb {I}}_j^1, {\mathbb {I}}_j^2, \dots , {\mathbb {I}}_j^d\right) \right\| _p}^p \\&= {\left\| \left( {\varvec{x}}^1\otimes {\varvec{x}}^2\otimes \dots \otimes {\varvec{x}}^d\right) \left( {\mathbb {I}}^1, {\mathbb {I}}^2, \dots , {\mathbb {I}}^d\right) \right\| _p}^p \\&= {\left\| {\varvec{x}}^1\otimes {\varvec{x}}^2\otimes \dots \otimes {\varvec{x}}^d\right\| _p}^p \\&= \left( \prod _{k=1}^d \Vert {\varvec{x}}^k\Vert _p\right) ^p \\&= 1. \end{aligned}$$
  3. (3)

    The lower bound of \(\Vert {\mathcal {T}}\Vert _{p_*}\) in (7).

    For any \({\mathcal {X}}\in {\mathbb {R}}^{n_1\times n_2\times \dots \times n_d}\), let \({\mathcal {X}}_j={\mathcal {X}}\left( {\mathbb {I}}_j^1, {\mathbb {I}}_j^2, \dots , {\mathbb {I}}_j^d\right)\) for \(j=1,2,\dots ,m\), i.e., \(\left\{ {\mathcal {X}}_1,{\mathcal {X}}_2,\dots ,{\mathcal {X}}_m\right\}\) is an arbitrary partition of \({\mathcal {X}}\). By the upper bound of (6) proved in (2), we have

    $$\begin{aligned} \sum _{j=1}^m {\Vert {\mathcal {X}}_j\Vert _{p_\sigma }}^q\le 1\Longrightarrow \Vert {\mathcal {X}}\Vert _{p_\sigma }\le 1. \end{aligned}$$

    Therefore, according to the dual property in Lemma 2.5, we have

    $$\begin{aligned} \Vert {\mathcal {T}}\Vert _{p_*}=\max _{\Vert {\mathcal {X}}\Vert _{p_\sigma }\le 1}\langle {\mathcal {T}},{\mathcal {X}}\rangle =\max _{\Vert {\mathcal {X}}\Vert _{p_\sigma }\le 1} \sum _{j=1}^m \langle {\mathcal {T}}_j,{\mathcal {X}}_j\rangle \ge \max _{\sum _{j=1}^m {\Vert {\mathcal {X}}_j\Vert _{p_\sigma }}^q\le 1} \sum _{j=1}^m \langle {\mathcal {T}}_j,{\mathcal {X}}_j\rangle . \end{aligned}$$
    (9)

    For \(j=1,2,\dots ,m\), let \(y_j=\Vert {\mathcal {X}}_j\Vert _{p_\sigma }\ge 0\) and further let \({\mathcal {Z}}_j=\frac{{\mathcal {X}}_j}{y_j}\) if \(y_j> 0\) or \({\mathcal {Z}}_j={\mathcal {O}}\) if \(y_j=0\). Clearly \(\Vert {\mathcal {Z}}_j\Vert _{p_\sigma }\le 1\) and we have

    $$\begin{aligned} \sum _{j=1}^m {\Vert {\mathcal {X}}_j\Vert _{p_\sigma }}^q\le 1 \Longleftrightarrow \sum _{j=1}^m {y_j}^q\le 1,\,y_j\ge 0,\,\Vert {\mathcal {Z}}_j\Vert _{p_\sigma }\le 1,\,j=1,2,\dots ,m. \end{aligned}$$

    Therefore, (9) further leads to

    $$\begin{aligned} \Vert {\mathcal {T}}\Vert _{p_*}&\ge \max _{\sum _{j=1}^m {y_j}^q\le 1, \,y_j\ge 0, \,\Vert {\mathcal {Z}}_j\Vert _{p_\sigma }\le 1,\,j=1,2,\dots ,m} \sum _{j=1}^m \langle {\mathcal {T}}_j,y_j{\mathcal {Z}}_j\rangle \\&=\max _{\sum _{j=1}^m {y_j}^q\le 1,\,y_j\ge 0,\,j=1,2,\dots ,m} \left( \max _{\Vert {\mathcal {Z}}_j\Vert _{p_\sigma }\le 1,\,j=1,2,\dots ,m} \sum _{j=1}^m y_j\langle {\mathcal {T}}_j,{\mathcal {Z}}_j\rangle \right) \\&= \max _{\sum _{j=1}^m {y_j}^q\le 1,\,y_j\ge 0,\,j=1,2,\dots ,m} \left( \sum _{j=1}^m y_j \max _{\Vert {\mathcal {Z}}_j\Vert _{p_\sigma }\le 1}\langle {\mathcal {T}}_j,{\mathcal {Z}}_j\rangle \right) \\&=\max _{\sum _{j=1}^m {y_j}^q\le 1,\,y_j\ge 0,\,j=1,2,\dots ,m} \sum _{j=1}^m y_j \Vert {\mathcal {T}}_j\Vert _{p_*} \\&=\left\| \left( \Vert {\mathcal {T}}_1\Vert _{p_*},\Vert {\mathcal {T}}_2\Vert _{p_*},\dots ,\Vert {\mathcal {T}}_m\Vert _{p_*}\right) \right\| _p, \end{aligned}$$

    where the second equality is due to the nonnegativity of \(y_j\) and \(\max _{\Vert {\mathcal {Z}}_j\Vert _{p_\sigma }\le 1}\langle {\mathcal {T}}_j,{\mathcal {Z}}_j\rangle\) for any \(1\le j\le m\), the third equality is due to the dual norm property, and the last equality is due to the tightness of the Hölder’s inequality.

  4. (4)

    The upper bound of \(\Vert {\mathcal {T}}\Vert _{p_*}\) in (7).

    For every \(j=1,2,\dots ,m\), let \({\mathcal {T}}'_j\in {\mathbb {R}}^{n_1\times n_2\times \dots \times n_d}\) where

    $$\begin{aligned} \left( t'_j\right) _{i_1i_2\dots i_d} = \left\{ \begin{array}{ll} t_{i_1i_2\dots i_d} &{} \quad \left( i_1,i_2,\dots ,i_d\right) \in {\mathbb {I}}^1_j\times {\mathbb {I}}^2_j\times \dots \times {\mathbb {I}}^d_j, \\ 0 &{} \quad \left( i_1,i_2,\dots ,i_d\right) \notin {\mathbb {I}}^1_j\times {\mathbb {I}}^2_j\times \dots \times {\mathbb {I}}^d_j. \end{array} \right. \end{aligned}$$

    By applying a similar approach as we prove (1), it is not difficult to get \(\Vert {\mathcal {T}}'_j\Vert _{p_*}=\Vert {\mathcal {T}}_j\Vert _{p_*}\) for any \(1\le j\le m\). Since \(\left\{ {\mathbb {I}}_j^1 \times {\mathbb {I}}_j^2 \times \dots \times {\mathbb {I}}_j^d: j=1,2,\dots ,m\right\}\) is a partition of \(\left\{ {\mathbb {I}}^1 \times {\mathbb {I}}^2 \times \dots \times {\mathbb {I}}^d\right\}\), we have \({\mathcal {T}}=\sum _{j=1}^m {\mathcal {T}}'_j\). Therefore, by the triangle inequality, we have

    $$\begin{aligned} \Vert {\mathcal {T}}\Vert _{p_*} = \left\| \sum _{j=1}^m {\mathcal {T}}'_j \right\| _{p_*} \le \sum _{j=1}^m \Vert {\mathcal {T}}'_j \Vert _{p_*} = \sum _{j=1}^m \Vert {\mathcal {T}}_j \Vert _{p_*}, \end{aligned}$$

    proving the last bound.

\(\square\)

Theorem 3.1 generalizes and answers affirmatively the conjecture in [14], which is for \(p=2\) and a tensor partition (a special case of arbitrary partition):

Conjecture 3.2

[14, Conjecture 3.5] If\(\left\{ {\mathcal {T}}_1,{\mathcal {T}}_2,\dots ,{\mathcal {T}}_m\right\}\)is a tensor partition ofa tensor\({\mathcal {T}}\), then

$$\begin{aligned} \left\| \left( \Vert {\mathcal {T}}_1\Vert _{2_\sigma },\Vert {\mathcal {T}}_2\Vert _{2_\sigma },\dots ,\Vert {\mathcal {T}}_m\Vert _{2_\sigma }\right) \right\| _\infty&\le \Vert {\mathcal {T}}\Vert _{2_\sigma } \le \left\| \left( \Vert {\mathcal {T}}_1\Vert _{2_\sigma },\Vert {\mathcal {T}}_2\Vert _{2_\sigma },\dots ,\Vert {\mathcal {T}}_m\Vert _{2_\sigma }\right) \right\| _2, \\ \left\| \left( \Vert {\mathcal {T}}_1\Vert _{2_*},\Vert {\mathcal {T}}_2\Vert _{2_*},\dots ,\Vert {\mathcal {T}}_m\Vert _{2_*}\right) \right\| _2&\le \Vert {\mathcal {T}}\Vert _{2_*} \le \left\| \left( \Vert {\mathcal {T}}_1\Vert _{2_*},\Vert {\mathcal {T}}_2\Vert _{2_*},\dots ,\Vert {\mathcal {T}}_m\Vert _{2_*}\right) \right\| _1. \end{aligned}$$

Theorem 3.1 also provides an alternative proof of a more special case which is for \(p=2\) and a regular partition (a special case of tensor partition) in [14, Theorem 3.1], whose proof is based on mathematical induction and heavily relies on the recursive structure in the definition of a regular partition. The novelty of the proof of Theorem 3.1 lies in establishing an index system to describe arbitrary partitions. It also provides a clearer picture relating the subtensors to the original tensor.

4 Discussions and theoretical applications

The general bounds on the tensor spectral p-norm and nuclear p-norm in Theorem 3.1 provide more insights on dealing with particular tensor instances in practice. Unlike the traditional matrix unfolding technique in which one needs to unfold a tensor in a fixed way, the flexibility on arbitrary partitions of a tensor provides more tools to estimate tensor norms of given tensor data in applications. In particular, it is useful for some tensors comprised of pieces with known spectral or nuclear p-norms. Let us look into its theoretical applications and see how these bounds connect to other tensor norm bounds in the literature.

We first check the tightness of the bounds in Theorem 3.1. Given the flexibility of arbitrary partitions, it is impossible to provide a general necessary and sufficient condition for these bounds to be tight. A trial sufficient condition for all the bounds in Theorem 3.1 to be tight is that all but one of \({\mathcal {T}}_j\)’s are zero tensors. The other obvious case is for \(p=1\) and \(q=\infty\), under which Theorem 3.1 is reduced to

$$\begin{aligned} \Vert {\mathcal {T}}\Vert _{1_{\sigma }}&= \left\| \left( \Vert {\mathcal {T}}_1\Vert _{1_{\sigma }},\Vert {\mathcal {T}}_2\Vert _{1_{\sigma }},\dots , \Vert {\mathcal {T}}_m\Vert _{1_{\sigma }}\right) \right\| _\infty , \\ \Vert {\mathcal {T}}\Vert _{1_*}&= \left\| \left( \Vert {\mathcal {T}}_1\Vert _{1_*},\Vert {\mathcal {T}}_2\Vert _{1_*},\dots ,\Vert {\mathcal {T}}_m\Vert _{1_*}\right) \right\| _1. \end{aligned}$$

These identities can also be verified by Proposition 2.6 where \(\Vert {\mathcal {T}}\Vert _{1_\sigma }=\Vert {\mathcal {T}}\Vert _\infty\) and \(\Vert {\mathcal {T}}\Vert _{1_*}=\Vert {\mathcal {T}}\Vert _1\).

One interesting case is for rank-one tensors, which was already observed in [14] for \(p=2\) and a regular partition.

Proposition 4.1

If\(\left\{ {\mathcal {T}}_1,{\mathcal {T}}_2,\dots ,{\mathcal {T}}_m\right\}\)is an arbitrarypartition of a rank-one tensor\({\mathcal {T}}\), then

$$\begin{aligned} \left\| \left( \Vert {\mathcal {T}}_1\Vert _{p_\sigma },\Vert {\mathcal {T}}_2\Vert _{p_\sigma },\dots ,\Vert {\mathcal {T}}_m\Vert _{p_\sigma }\right) \right\| _q = \Vert {\mathcal {T}}\Vert _{p_\sigma } = \Vert {\mathcal {T}}\Vert _{q_*} = \left\| \left( \Vert {\mathcal {T}}_1\Vert _{q_*},\Vert {\mathcal {T}}_2\Vert _{q_*},\dots ,\Vert {\mathcal {T}}_m\Vert _{q_*}\right) \right\| _q. \end{aligned}$$
(10)

Proof

Let \({\mathcal {T}}=\left( t_{i_1i_2\dots i_d}\right) \in {\mathbb {R}}^{n_1\times n_2\times \dots \times n_d}\) and \({\mathcal {T}}_j={\mathcal {T}}\left( {\mathbb {I}}^1_j,{\mathbb {I}}^2_j,\dots ,{\mathbb {I}}^d_j\right)\) where \({\mathbb {I}}^k_j\in {\mathbb {I}}^k\) for all k and all j. Observe that \(\left\{ t_{i_1i_2\dots i_d}\in {\mathbb {R}}^{1\times 1\times \dots \times 1}: \left( i_1,i_2,\dots ,i_d\right) \in {\mathbb {I}}^1_j\times {\mathbb {I}}^2_j\times \dots \times {\mathbb {I}}^d_j\right\}\) is an arbitrary partition of \({\mathcal {T}}_j\) for every j. Noticing that any scalar \(x\in {\mathbb {R}}\) has \(\Vert x\Vert _{p_\sigma }=\Vert x\Vert _{p_*}=|x|\), by applying the upper bound of (6) for \({\mathcal {T}}\) and every \({\mathcal {T}}_j~\left( 1\le j\le m\right)\), one has

$$\begin{aligned} \Vert {\mathcal {T}}\Vert _{p_\sigma }\le & {} \left\| \left( \Vert {\mathcal {T}}_1\Vert _{p_\sigma },\Vert {\mathcal {T}}_2\Vert _{p_\sigma },\dots ,\Vert {\mathcal {T}}_m\Vert _{p_\sigma }\right) \right\| _q\nonumber \\\le & {} \left( \sum _{i_1=1}^{n_1}\sum _{i_2=1}^{n_2} \dots \sum _{i_d=1}^{n_d} {\Vert t_{i_1i_2\dots i_d}\Vert _{p_\sigma }}^q\right) ^{\frac{1}{q}}= \Vert {\mathcal {T}}\Vert _q, \end{aligned}$$
(11)

and by applying the lower bound of (7) one also has

$$\begin{aligned} \Vert {\mathcal {T}}\Vert _q= & {} \left( \sum _{i_1=1}^{n_1}\sum _{i_2=1}^{n_2} \dots \sum _{i_d=1}^{n_d} {\Vert t_{i_1i_2\dots i_d}\Vert _{q_*}}^q\right) ^{\frac{1}{q}}\nonumber \\\le & {} \left\| \left( \Vert {\mathcal {T}}_1\Vert _{q_*},\Vert {\mathcal {T}}_2\Vert _{q_*},\dots ,\Vert {\mathcal {T}}_m\Vert _{q_*}\right) \right\| _q\le \Vert {\mathcal {T}}\Vert _{q_*}. \end{aligned}$$
(12)

On the other hand, as \({\mathcal {T}}\) is rank-one, one has \(\Vert {\mathcal {T}}\Vert _{p_\sigma }=\Vert {\mathcal {T}}\Vert _q=\Vert {\mathcal {T}}\Vert _{q_*}\) according to Proposition 2.4. By combining it with (11) and (12), we are lead to the final identity (10). \(\square\)

As we see from the above discussion, both the upper and lower bounds in Theorem 3.1 can be obtained for various cases. In general, the more subtensors in an arbitrary partition, the larger gap between the lower and upper bounds for a generic tensor. In particular, if a partition has m subtensors, the largest possible gap between the lower and upper bounds can be \(m^{\frac{1}{q}}\) when all subtensors have the same spectral p-norm or nuclear p-norm. In an extreme though trivial case where there is only one subtensor in the partition (the original tensor itself), all the bounds become naturally tight. However, due to the curse of dimensionality and the NP-hardness to compute these norms, the larger the subtensors, the more difficulty and inaccuracy in estimating these norms.

We now discuss the main bounds in some special cases to relate existing bounds in the literature. By applying the finest partition \({\mathcal {T}}=\left\{ t_{i_1i_2\dots i_d}\in {\mathbb {R}}^{1\times 1\times \dots \times 1}: \left( i_1,i_2,\dots ,i_d\right) \in {\mathbb {I}}^1\times {\mathbb {I}}^2\times \dots \times {\mathbb {I}}^d\right\}\) to Theorem 3.1, we obtain the following bounds among tensor norms.

Proposition 4.2

For any tensor\({\mathcal {T}}\)and\(1\le p,q\le \infty\)with\(\frac{1}{p}+\frac{1}{q}=1\),

$$\begin{aligned} \Vert {\mathcal {T}}\Vert _\infty \le \Vert {\mathcal {T}}\Vert _{p_\sigma } \le \Vert {\mathcal {T}}\Vert _q \le \Vert {\mathcal {T}}\Vert _{q_*} \le \Vert {\mathcal {T}}\Vert _1. \end{aligned}$$
(13)

The second inequality of (13), \(\Vert {\mathcal {T}}\Vert _{p_\sigma } \le \Vert {\mathcal {T}}\Vert _q\), is exactly the one in [23, Theorem 20], and hence it provides an alternatively proof of the upper bound of the tensor spectral p-norm. When \(p=2\), (13) also implies the bounds proposed in [4, Lemma 9.1]:

$$\begin{aligned} \frac{1}{\sqrt{\prod _{k=1}^d n_k}}\Vert {\mathcal {T}}\Vert _2 \le \Vert {\mathcal {T}}\Vert _{2_\sigma } \le \Vert {\mathcal {T}}\Vert _2 \le \Vert {\mathcal {T}}\Vert _{2_*} \le \sqrt{\prod _{k=1}^d n_k}\, \Vert {\mathcal {T}}\Vert _2. \end{aligned}$$

Next, we apply partitions to vector fibers of \({\mathcal {T}}\) to Theorem 3.1, say mode-d fibers, i.e.,

$$\begin{aligned} {\mathcal {T}}=\left\{ {\varvec{t}}_{i_1i_2\dots i_{d-1}}\in {\mathbb {R}}^{n_d}: \left( i_1,i_2,\dots ,i_{d-1}\right) \in {\mathbb {I}}^1\times {\mathbb {I}}^2\times \dots \times {\mathbb {I}}^{d-1}\right\} . \end{aligned}$$

The bounds tighten that of (13) to the followings:

Proposition 4.3

For any tensor\({\mathcal {T}}\)and\(1\le p,q\le \infty\)with\(\frac{1}{p}+\frac{1}{q}=1\),

$$\begin{aligned} \max _{i_k\in {\mathbb {I}}^k,\,k=1,2,\dots ,{d-1}}\Vert {\varvec{t}}_{i_1i_2\dots i_{d-1}}\Vert _q\le & {} \Vert {\mathcal {T}}\Vert _{p_\sigma } \le \Vert {\mathcal {T}}\Vert _q \le \Vert {\mathcal {T}}\Vert _{q_*}\le\sum _{i_k\in {\mathbb {I}}^k,\,k=1,2,\dots ,d-1}\Vert {\varvec{t}}_{i_1i_2\dots i_{d-1}}\Vert _q. \end{aligned}$$
(14)

The first inequality of (14) is exactly the one in [23, Proposition 22]. When \(p=2\) and suppose that \(n_d=\max _{1\le k\le d}n_k\), the first inequality of (14) also implies the bound in [29, Corollary 4.9]:

$$\begin{aligned} \Vert {\mathcal {T}}\Vert _2 \le \sqrt{\prod _{k=1}^{d-1} n_k } \Vert {\mathcal {T}}\Vert _{2_\sigma }. \end{aligned}$$

This is because the largest gap between the lowest and highest bounds in (14) is \(\sqrt{\prod _{k=1}^{d-1} n_k}\).

Let us now apply partitions to matrix slices and discuss their connections to matrix unfoldings. Matrix unfoldings of a tensor have been one of the main tools to study tensor computation and optimization problems, mainly due to the fact that most tensor problems are NP-hard [10] while the corresponding matrix problems are much easier. One important example is that for the tensor spectral norm and nuclear norm, both are NP-hard when the order of the tensor \(d\ge 3\), while they can be computed in polynomial time for a matrix (\(d=2\)). In practice, the tensor nuclear norm is widely used in tensor completion [5, 20] as a convex envelope of the tensor rank. In some literature, even the tensor nuclear norm is defined by the average nuclear norms of its matrix unfoldings, as this definition, albeit is different to the original definition, can be computed in polynomial time.

When \(p=2\), for the tensor spectral norm, the relations of a tensor and its matrix unfoldings have been studied widely, while that for the tensor nuclear norm was only addressed by Hu [13] and soon again by Friedland and Lim [4]. Wang et al. [29] studied comprehensively on the spectral p-norm based on various matrix unfoldings as well as tensor unfoldings. One obvious way to apply Theorem 3.1 is to partition a tensor into matrix slices. To make a clearer presentation, we mainly discuss third order tensors, which can be easily generalized to higher orders. Let \({\mathcal {T}}\in {\mathbb {R}}^{n_1\times n_2\times n_3}\). Denote \({\text {Mat}}_1\left( {\mathcal {T}}\right) \in {\mathbb {R}}^{n_1\times n_2n_3}\), \({\text {Mat}}_2\left( {\mathcal {T}}\right) \in {\mathbb {R}}^{n_2\times n_1n_3}\), and \({\text {Mat}}_3\left( {\mathcal {T}}\right) \in {\mathbb {R}}^{n_3\times n_1n_2}\) to be the mode-1, mode-2, and mode-3 unfolding matrix of \({\mathcal {T}}\), respectively. For \(k=1,2,3\), denote \(T^k_i\) to be the ith mode-k matrix slice for \(i=1,2,\dots ,n_k\); see the following example.

Example 4.4

Let \({\mathcal {T}}=\left( t_{ij\ell }\right) \in {\mathbb {R}}^{2\times 3\times 4}\) where \(i\in \{1,2\}\), \(j\in \{1,2,3\}\) and \(\ell \in \{1,2,3,4\}\), and we have

$$\begin{aligned} {\text {Mat}}_1\left( {\mathcal {T}}\right)&=\left( \begin{array}{cccccccccccc} t_{111} &{}\quad t_{112} &{}\quad t_{113} &{}\quad t_{114} &{}\quad t_{121} &{}\quad t_{122} &{}\quad t_{123} &{}\quad t_{124} &{}\quad t_{131} &{}\quad t_{132} &{}\quad t_{133} &{}\quad t_{134} \\ t_{211} &{}\quad t_{212} &{}\quad t_{213} &{}\quad t_{214} &{}\quad t_{221} &{}\quad t_{222} &{}\quad t_{223} &{}\quad t_{224} &{}\quad t_{231} &{}\quad t_{232} &{}\quad t_{233} &{}\quad t_{234} \\ \end{array} \right) , \\ {\text {Mat}}_2\left( {\mathcal {T}}\right)&=\left( \begin{array}{cccccccc} t_{111} &{}\quad t_{112} &{}\quad t_{113} &{}\quad t_{114} &{}\quad t_{211} &{}\quad t_{212} &{}\quad t_{213} &{}\quad t_{214} \\ t_{121} &{}\quad t_{122} &{}\quad t_{123} &{}\quad t_{124} &{}\quad t_{221} &{}\quad t_{222} &{}\quad t_{223} &{}\quad t_{224} \\ t_{131} &{}\quad t_{132} &{}\quad t_{133} &{}\quad t_{134} &{}\quad t_{231} &{}\quad t_{232} &{}\quad t_{233} &{}\quad t_{234} \\ \end{array} \right) , \\ {\text {Mat}}_3\left( {\mathcal {T}}\right)&=\left( \begin{array}{cccccc} t_{111} &{}\quad t_{121} &{}\quad t_{131} &{}\quad t_{211} &{}\quad t_{221} &{}\quad t_{231} \\ t_{112} &{}\quad t_{122} &{}\quad t_{132} &{}\quad t_{212} &{}\quad t_{222} &{}\quad t_{232} \\ t_{113} &{}\quad t_{123} &{}\quad t_{133} &{}\quad t_{213} &{}\quad t_{223} &{}\quad t_{233} \\ t_{114} &{}\quad t_{124} &{}\quad t_{134} &{}\quad t_{214} &{}\quad t_{224} &{}\quad t_{234} \\ \end{array} \right) , \\ T^1_1&=\left( \begin{array}{cccc} t_{111} &{}\quad t_{112} &{}\quad t_{113} &{}\quad t_{114} \\ t_{121} &{}\quad t_{122} &{}\quad t_{123} &{}\quad t_{124} \\ t_{131} &{}\quad t_{132} &{}\quad t_{133} &{}\quad t_{134} \\ \end{array} \right) , \\ T^1_2&=\left( \begin{array}{cccc} t_{211} &{}\quad t_{212} &{}\quad t_{213} &{}\quad t_{214} \\ t_{221} &{}\quad t_{222} &{}\quad t_{223} &{}\quad t_{224} \\ t_{231} &{}\quad t_{232} &{}\quad t_{233} &{}\quad t_{234} \\ \end{array} \right) . \end{aligned}$$

Let us first generalize the relations of the norms of a tensor and the norms of its matrix unfoldings, from the tensor spectral norm to the tensor spectral p-norm, and from the tensor nuclear norm [13] to the tensor nuclear p-norm.

Lemma 4.5

If\({\mathcal {T}}\in {\mathbb {R}}^{n_1\times n_2\times n_3}\)and\(1\le p\le \infty\), then for any\(\ell =1,2,3\),

$$\begin{aligned} \Vert {\mathcal {T}}\Vert _{p_\sigma }&\le \Vert {\text {Mat}}_\ell \left( {\mathcal {T}}\right) \Vert _{p_\sigma },\\ \Vert {\mathcal {T}}\Vert _{p_*}&\ge \Vert {\text {Mat}}_\ell \left( {\mathcal {T}}\right) \Vert _{p_*}. \end{aligned}$$

Proof

We prove the case for \(\ell =1\) as the other two cases are similar. Let \({\varvec{x}}^k\in {\mathbb {R}}^{n_k}\) with \(\Vert {\varvec{x}}^k\Vert _p=1\) for \(k=1,2,3\), such that \(\Vert {\mathcal {T}}\Vert _{p_\sigma }=\langle {\mathcal {T}}, {\varvec{x}}^1\otimes {\varvec{x}}^2\otimes {\varvec{x}}^3 \rangle\). By Proposition 2.1, \(\Vert {\varvec{x}}^2\otimes {\varvec{x}}^3\Vert _p=1\), and so \(\Vert {\text {vec}}\left( {\varvec{x}}^2\otimes {\varvec{x}}^3\right) \Vert _p=1\), where \({\text {vec}}\left( \varvec{\cdot }\right)\) turns a tensor or a matrix to a vector. Therefore,

$$\begin{aligned} \Vert {\mathcal {T}}\Vert _{p_\sigma }=\langle {\mathcal {T}}, {\varvec{x}}^1\otimes {\varvec{x}}^2\otimes {\varvec{x}}^3 \rangle = \langle {\text {Mat}}_1\left( {\mathcal {T}}\right) , {\varvec{x}}^1 \otimes {\text {vec}}\left( {\varvec{x}}^2\otimes {\varvec{x}}^3\right) \rangle \le \Vert {\text {Mat}}_1\left( {\mathcal {T}}\right) \Vert _{p_\sigma }. \end{aligned}$$

For the nuclear p-norm, let \({\mathcal {T}}=\sum _{i=1}^r \lambda _i {\varvec{y}}^1_i \otimes {\varvec{y}}^2_i \otimes {\varvec{y}}^3_i\) with \(\Vert {\varvec{y}}^k_i\Vert _p=1\) for all k and all i, such that \(\Vert {\mathcal {T}}\Vert _{p_*}=\sum _{i=1}^r |\lambda _i|\). It is not difficulty to see that

$$\begin{aligned} {\text {Mat}}_1\left( {\mathcal {T}}\right) = \sum _{i=1}^r \lambda _i {\varvec{y}}^1_i \otimes {\text {vec}}\left( {\varvec{y}}^2_i \otimes {\varvec{y}}^3_i\right) , \end{aligned}$$

and \({\text {vec}}\left( {\varvec{y}}^2_i \otimes {\varvec{y}}^3_i\right) \in {\mathbb {R}}^{n_2n_3}\) with \(\Vert {\text {vec}}\left( {\varvec{y}}^2_i \otimes {\varvec{y}}^3_i\right) \Vert _p=1\) for all i. Therefore,

$$\begin{aligned} \Vert {\text {Mat}}_1\left( {\mathcal {T}}\right) \Vert _{p_*}\le \sum _{i=1}^r |\lambda _i| = \Vert {\mathcal {T}}\Vert _{p_*}. \end{aligned}$$

\(\square\)

Our main result in this section discusses the relations of the norms of a tensor, the norms of matrix unfoldings of the tensor, and the norms obtained by partitions to matrix slices of the tensor, as follows.

Theorem 4.6

Let\({\mathcal {T}}\in {\mathbb {R}}^{n_1\times n_2\times n_3}\)and\(1\le p,q\le \infty\)with\(\frac{1}{p}+\frac{1}{q}=1\). For\(k=1,2,3\), denote

$$\begin{aligned} {\varvec{t}}^k_{p_\sigma }=&\left( \Vert T^k_1\Vert _{p_\sigma }, \Vert T^k_2\Vert _{p_\sigma },\dots ,\Vert T^k_{n_k}\Vert _{p_\sigma }\right) \in {\mathbb {R}}^{n_k}. \\ {\varvec{t}}^k_{p_*}=&\left( \Vert T^k_1\Vert _{p_*}, \Vert T^k_2\Vert _{p_*},\dots ,\Vert T^k_{n_k}\Vert _{p_*}\right) \in {\mathbb {R}}^{n_k}. \end{aligned}$$

It follows that for any\(k=1,2,3\)and any\(\ell \ne k\),

$$\begin{aligned} {n_k}^{-\frac{1}{q}}\Vert {\text {Mat}}_\ell \left( {\mathcal {T}}\right) \Vert _{p_\sigma } \le {n_k}^{-\frac{1}{q}} \left\| {\varvec{t}}^k_{p_\sigma } \right\| _q \le \left\| {\varvec{t}}^k_{p_\sigma }\right\| _\infty&\le \Vert {\mathcal {T}}\Vert _{p_\sigma } \le \Vert {\text {Mat}}_\ell \left( {\mathcal {T}}\right) \Vert _{p_\sigma } \le \left\| {\varvec{t}}^k_{p_\sigma }\right\| _q, \end{aligned}$$
(15)
$$\begin{aligned} {n_k}^{\frac{1}{q}}\Vert {\text {Mat}}_\ell \left( {\mathcal {T}}\right) \Vert _{p_*} \ge {n_k}^{\frac{1}{q}} \left\| {\varvec{t}}^k_{p_*} \right\| _p \ge \left\| {\varvec{t}}^k_{p_*}\right\| _1&\ge \Vert {\mathcal {T}}\Vert _{p_*} \ge \Vert {\text {Mat}}_\ell \left( {\mathcal {T}}\right) \Vert _{p_*} \ge \left\| {\varvec{t}}^k_{p_*}\right\| _p. \end{aligned}$$
(16)

Proof

A key observation is that for \(k\ne \ell\), \(\left\{ T^k_1,T^k_2,\dots ,T^k_{n_k}\right\}\) or \(\left\{ \left( T^k_1\right) ^{{\text {T}}},\left( T^k_2\right) ^{{\text {T}}},\dots ,\left( T^k_{n_k}\right) ^{{\text {T}}}\right\}\) must be an arbitrary partition of the matrix \({\text {Mat}}_\ell \left( {\mathcal {T}}\right)\) (see Example 4.4). By applying Theorem 3.1, the last inequality of (15) and the last inequality of (16) hold, and so as to the first inequality of (15) and the first inequality of (16). The fourth inequality of (15) and the fourth inequality of (16) hold by Lemma 4.5. The third inequality of (15) and the third inequality of (16) hold by Theorem 3.1. Finally, the second inequality of (15) holds by the largest gap between the \(L_q\)-norm and the \(L_\infty\)-norm of an \(n_k\)-dimensional vector, and the second inequality of (16) holds by the largest gap between the \(L_p\)-norm and the \(L_1\)-norm of an \(n_k\)-dimensional vector. \(\square\)

When \(p=2\), (16) provides tighter lower or upper bounds than that in [13, Theorem 4.4] and [4, Theorem 9.4]:

$$\begin{aligned} {n_k}^{-\frac{1}{2}}\Vert {\text {Mat}}_\ell \left( {\mathcal {T}}\right) \Vert _{2_\sigma }&\le \Vert {\mathcal {T}}\Vert _{2_\sigma } \le \Vert {\text {Mat}}_\ell \left( {\mathcal {T}}\right) \Vert _{2_\sigma } ,\\ {n_k}^{\frac{1}{2}}\Vert {\text {Mat}}_\ell \left( {\mathcal {T}}\right) \Vert _{2_*}&\ge \Vert {\mathcal {T}}\Vert _{2_*} \ge \Vert {\text {Mat}}_\ell \left( {\mathcal {T}}\right) \Vert _{2_*} . \end{aligned}$$

In general, by Theorem 4.6, both \(\left\| {\varvec{t}}^k_{p_\sigma }\right\| _q\) obtained from partitions to matrix slices and \(\Vert {\text {Mat}}_\ell \left( {\mathcal {T}}\right) \Vert _{p_\sigma }\) obtained from matrix unfoldings, provide a bound with a factor \({n_k}^{\frac{1}{q}}\) for \(\Vert {\mathcal {T}}\Vert _{p_\sigma }\). The same factor \({n_k}^{\frac{1}{q}}\) for \(\Vert {\mathcal {T}}\Vert _{p_*}\) by both \(\left\| {\varvec{t}}^k_{p_*}\right\| _p\) from partitions to matrix slices and \(\Vert {\text {Mat}}_\ell \left( {\mathcal {T}}\right) \Vert _{p_*}\) from matrix unfoldings. For the flexibility of \(n_k\)’s in Theorem 4.6, one may choose the tightest bound to be \(\min _{1\le k\le 3} {n_k}^{\frac{1}{q}}\). Finally, by choosing one bound from the best matrix unfolding and the other from the best partition to matrix slices would give the tightest bound of both the tensor spectral p-norm and the tensor nuclear p-norm.

It is not difficult to extend Theorem 4.6 to fourth or higher order tensors. Again, the bounds in terms of \(n_k\)’s, the dimensions of a tensor, are similarly obtained from matrix unfoldings and from partitions to matrix slices, and can be tighter by combining the two. We only list the following result to extend Theorem 4.6 to a general order, whose proof is left to interested readers.

Theorem 4.7

Let\({\mathcal {T}}\in {\mathbb {R}}^{n_1\times n_2\times \dots \times n_d}\)and\(1\le p,q\le \infty\)with\(\frac{1}{p}+\frac{1}{q}=1\). Let\(\left\{ {\mathbb {I}}_1,{\mathbb {I}}_2\right\}\)be a partition of the set\(\{1,2,\dots ,d\}\), and pick any\(i\in {\mathbb {I}}_1\)and\(j\in {\mathbb {I}}_2\). Denote\({\text {Mat}}({\mathcal {T}})\)to be the matrix unfolding of\({\mathcal {T}}\)by combining modesof\({\mathbb {I}}_1\)into the row index and modes of\({\mathbb {I}}_2\)into the columnindex, i.e., a\(\left( \prod _{k\in {\mathbb {I}}_1} n_k\right) \times \left( \prod _{k\in {\mathbb {I}}_2} n_k\right)\)matrix. Consider the set ofmatrix slices of\({\mathcal {T}}\)obtained by fixing all the mode-kindicesexcept modesiandj, i.e., a set of\(\prod _{1\le k\le d,\,k\ne i,j}n_k\)number of\(n_i\times n_j\)matrices. Further, denote\({\varvec{t}}_{p_\sigma }\in {\mathbb {R}}^{\prod _{1\le k\le d,\,k\ne i,j}n_k}\)to be the vector whose entries are the spectralp-norms of this set ofmatrix slices and\({\varvec{t}}_{p_*}\in {\mathbb {R}}^{\prod _{1\le k\le d,\,k\ne i,j}n_k}\)to be the vector whose entries are the nuclearp-norm ofthis set of matrix slices. It follows that

$$\begin{aligned} \Vert {\text {Mat}}\left( {\mathcal {T}}\right) \Vert _{p_\sigma }\prod _{1\le k\le d,\,k\ne i,j}{n_k}^{-\frac{1}{q}} \! \le \left\| {\varvec{t}}_{p_\sigma } \right\| _q \prod _{1\le k\le d,\,k\ne i,j}{n_k}^{-\frac{1}{q}} \! \le \left\| {\varvec{t}}_{p_\sigma }\right\| _\infty \le \Vert {\mathcal {T}}\Vert _{p_\sigma } \le \Vert {\text {Mat}}\left( {\mathcal {T}}\right) \Vert _{p_\sigma } \le \left\| {\varvec{t}}_{p_\sigma }\right\| _q,\\ \Vert {\text {Mat}}\left( {\mathcal {T}}\right) \Vert _{p_*} \prod _{1\le k\le d,\,k\ne i,j}{n_k}^{\frac{1}{q}} \! \ge \left\| {\varvec{t}}_{p_*} \right\| _p \prod _{1\le k\le d,\,k\ne i,j}{n_k}^{\frac{1}{q}} \! \ge \left\| {\varvec{t}}_{p_*}\right\| _1 \ge \Vert {\mathcal {T}}\Vert _{p_*} \ge \Vert {\text {Mat}}\left( {\mathcal {T}}\right) \Vert _{p_*} \ge \left\| {\varvec{t}}_{p_*}\right\| _p. \end{aligned}$$

We remark that Theorem 4.7 indicates any matrix unfolding, not necessarily having \(n_i\) rows and \(\prod _{1\le k\le d,\,k\ne i}n_k\) columns such as third order tensors. In this sense for \(p=2\), it extends the result in [13, Theorem 5.2]. Finally, we remark that one can even use the tensor unfolding technique [29] to derive more sophisticated bounds, but we do not pursue here as it involves heavy notations on the partition lattice of modes. The key point leading to all of these is the following fact: For any tensor unfolding of a tensor, there exists a partition of the original tensor, such that it is also a partition of the tensor unfolding.