An alternating direction method with increasing penalty for stable principal component pursuit

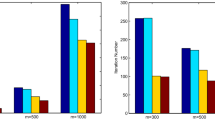
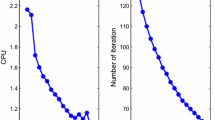
Abstract

The stable principal component pursuit (SPCP) is a non-smooth convex optimization problem, the solution of which enables one to reliably recover the low rank and sparse components of a data matrix which is corrupted by a dense noise matrix, even when only a fraction of data entries are observable. In this paper, we propose a new algorithm for solving SPCP. The proposed algorithm is a modification of the alternating direction method of multipliers (ADMM) where we use an increasing sequence of penalty parameters instead of a fixed penalty. The algorithm is based on partial variable splitting and works directly with the non-smooth objective function. We show that both primal and dual iterate sequences converge under mild conditions on the sequence of penalty parameters. To the best of our knowledge, this is the first convergence result for a variable penalty ADMM when penalties are not bounded, the objective function is non-smooth and its sub-differential is not uniformly bounded. Using partial variable splitting and adopting an increasing sequence of penalty multipliers, together, significantly reduce the number of iterations required to achieve feasibility in practice. Our preliminary computational tests show that the proposed algorithm works very well in practice, and outperforms ASALM, a state of the art ADMM algorithm for the SPCP problem with a constant penalty parameter.

Appendix: Proofs

1.1 Proof of Lemma 1

Suppose $\delta >0$. Let $(Z^*,S^*)$ be an optimal solution to problem $(P_{ns})$, $\theta ^*$ denote the optimal Lagrangian multiplier for the constraint $(Z,S)\in \chi$ written as $\frac{1}{2}\Vert \pi _{\varOmega }\left( Z+S-D\right) \Vert ^2_F\le \frac{\delta ^2}{2}$ and $\pi ^*_{\varOmega }$ denotes the adjoint operator of $\pi _{\varOmega }$. Note that $\pi ^*_{\varOmega }=\pi _{\varOmega }$. Then the KKT conditions for this problem are given by

$$\begin{aligned} Q+\rho (Z^*-\tilde{Z})+\theta ^*~\pi _{\varOmega }\left( Z^*+S^*-D\right)= & {} 0, \end{aligned}$$

(38)

$$\begin{aligned} \xi G + \theta ^*~\pi _{\varOmega }\left( Z^*+S^*-D\right)= & {} 0, \quad G\in \partial \Vert S^*\Vert _1, \end{aligned}$$

(39)

$$\begin{aligned} \Vert \pi _{\varOmega }\left( Z^*+S^*-D\right) \Vert _F\le & {} \delta , \end{aligned}$$

(40)

$$\begin{aligned} \theta ^*\ge & {} 0, \end{aligned}$$

(41)

$$\begin{aligned} \theta ^*~\left( \Vert \pi _{\varOmega }\left( Z^*+S^*-D\right) \Vert _F-\delta \right)= & {} 0, \end{aligned}$$

(42)

where (38) and (39) follow from the fact that $\pi _{\varOmega } \pi _{\varOmega }=\pi _{\varOmega }$.

From (38) and (39), we get

$$\begin{aligned} \pi _{{\varOmega }^c}\left( Z^*\right) =\pi _{{\varOmega }^c}\left( q(\tilde{Z})\right) , \quad \pi _{{\varOmega }^c}\left( G\right) =\mathbf{0} \end{aligned}$$

(43)

and

$$\begin{aligned} \left[ \begin{array}{c@{\quad }c} (\rho +\theta ^*)I &{} \theta ^*I\\ \theta ^*I &{} \theta ^*I \\ \end{array} \right] \left[ \begin{array}{c} \pi _{\varOmega }\left( Z^*\right) \\ \pi _{\varOmega }\left( S^*\right) \\ \end{array} \right] = \left[ \begin{array}{c} \pi _{\varOmega }\left( \theta ^*~D+\rho ~q(\tilde{Z})\right) \\ \pi _{\varOmega }\left( \theta ^*~D-\xi G\right) \\ \end{array} \right] , \end{aligned}$$

(44)

where $q(\tilde{Z})=\tilde{Z}-\rho ^{-1}~Q$. From (44) it follows that

$$\begin{aligned} \left[ \begin{array}{c@{\quad }c} (\rho +\theta ^*)I &{} \theta ^*I\\ 0 &{} \left( \frac{\rho \theta ^*}{\rho +\theta ^*}\right) ~I \\ \end{array} \right] \left[ \begin{array}{c} \pi _{\varOmega }\left( Z^*\right) \\ \pi _{\varOmega }\left( S^*\right) \\ \end{array} \right] = \left[ \begin{array}{c} \pi _{\varOmega }\left( \theta ^*~D+\rho ~q(\tilde{Z})\right) \\ \frac{\rho \theta ^*}{\rho +\theta ^*}~\pi _{\varOmega }\left( D-q(\tilde{Z})\right) -\xi \pi _{\varOmega }\left( G\right) \\ \end{array} \right] . \nonumber \\ \end{aligned}$$

(45)

From the second equation in (45), we get

$$\begin{aligned} \xi \frac{(\rho +\theta ^*)}{\rho \theta ^*}~\pi _{\varOmega }\left( G\right) +\pi _{\varOmega }\left( S^*\right) +\pi _{\varOmega }\left( q(\tilde{Z})-D\right) =0. \end{aligned}$$

(46)

The Eq. (46) and $\pi _{{\varOmega }^c}\left( G\right) =\mathbf{0}$ are precisely the first-order optimality conditions for the “shrinkage” problem

$$\begin{aligned} \min _{S\in \mathbb {R}^{m\times n}}\left\{ \xi \frac{(\rho +\theta ^*)}{\rho \theta ^*} \Vert S\Vert _1+\frac{1}{2}\Vert S+\pi _{\varOmega }\left( q(\tilde{Z})-D\right) \Vert _F^2\right\} . \end{aligned}$$

The expression for $S^*$ in (10) is the optimal solution to this “shrinkage” problem, and $Z^*$ given in (11) follows from the first equation in (43) and the first row of (45). Hence, given optimal Lagrangian dual $\theta ^*$, $S^*$ and $Z^*$ computed from Eqs. (10) and (11), respectively, satisfy KKT conditions (38) and (39).

Next, we show how to compute the optimal dual $\theta ^*$. We consider two cases.

• (i) Suppose $\Vert \pi _{\varOmega }\left( D-q(\tilde{Z})\right) \Vert _F\le \delta$. In this case, let $\theta ^*=0$. Setting $\theta ^*=0$ in (10) and (11), we find $S^*=\mathbf{0}$ and $Z^*=q(\tilde{Z})$. By construction, $S^*$, $Z^*$ and $\theta ^*$ satisfy conditions (38) and (39). It is easy to check that this choice of $\theta ^*=0$ trivially satisfies the rest of the conditions as well. Hence, $\theta ^*=0$ is an optimal lagrangian dual.

• (ii) Next, suppose $\Vert \pi _{\varOmega }\left( D-q(\tilde{Z})\right) \Vert _F>\delta$. From (11), we have

  $$\begin{aligned} \pi _{\varOmega }\left( Z^*+S^*-D\right) = \frac{\rho }{\rho +\theta ^*}~\pi _{\varOmega }\left( S^*+q(\tilde{Z})-D\right) . \end{aligned}$$

  (47)

  Therefore,

  $$\begin{aligned}&\Vert \pi _{\varOmega }\left( Z^*+S^*-D\right) \Vert _F \nonumber \\&\quad =\frac{\rho }{\rho +\theta ^*}~\left\| \pi _{\varOmega }\left( S^*+q(\tilde{Z})-D\right) \right\| _F, \nonumber \\&\quad =\frac{\rho }{\rho +\theta ^*} \left\| \pi _{\varOmega }\left( \max \left\{ |D-q(\tilde{Z})| -\xi \frac{(\rho +\theta ^*)}{\rho \theta ^*} E,\ \mathbf{0}\right\} -|D-q(\tilde{Z})|\right) \right\| _F,\nonumber \\&\quad = \frac{\rho }{\rho +\theta ^*}~\left\| \pi _{\varOmega }\left( \min \left\{ \xi \frac{(\rho +\theta ^*)}{\rho \theta ^*}~E,\ |D-q(\tilde{Z})|\right\} \right) \right\| _F,\nonumber \\&\quad =\left\| \min \left\{ \frac{\xi }{\theta ^*}~E,\ \frac{\rho }{\rho +\theta ^*}~\left| \pi _{\varOmega }\left( D-q(\tilde{Z})\right) \right| \right\} \right\| _F, \end{aligned}$$

  (48)

  where the second equation is obtained after substituting (10) for $S^*$ and then componentwise dividing the resulting expression inside the norm by $\hbox {sgn}\left( D-q(\tilde{Z})\right)$. Define $\phi :\mathbb {R}_+\rightarrow \mathbb {R}$,

  $$\begin{aligned} \phi (\theta ):= \left\| \min \left\{ \frac{\xi }{\theta }~E,\ \frac{\rho }{\rho +\theta }~\left| \pi _{\varOmega }\left( D-q(\tilde{Z})\right) \right| \right\} \right\| _F. \end{aligned}$$

  (49)

  It is easy to show that $\phi$ is a strictly decreasing function of $\theta$. Since $\lim _{\theta \rightarrow \infty }\phi (\theta )=0$ and $\phi (0)=\Vert \pi _{\varOmega }\left( D-q(\tilde{Z})\right) \Vert _F>\delta$, there exists a unique $\theta ^*>0$ such that $\phi (\theta ^*)=\delta$. Moreover, since $\theta ^*>0$ and $\phi (\theta ^*)=\delta$, (48) implies that $Z^*$, $S^*$ and $\theta ^*$ satisfy the rest of KKT conditions (40), (41) and (42) as well. Thus, the unique $\theta ^*>0$ that satisfies $\phi (\theta ^*)=\delta$ is the optimal Lagrangian dual. We now show that $\theta ^*$ can be computed in $\mathcal {O}(|{\varOmega }|\log (|{\varOmega }|))$ time. Let $A:=|\pi _{\varOmega }\left( D-q(\tilde{Z})\right) |$ and $0\le a_{(1)}\le a_{(2)}\le \cdots \le a_{(|{\varOmega }|)}$ be the $|{\varOmega }|$ elements of the matrix $A$ corresponding to the indices $(i,j)\in {\varOmega }$ sorted in increasing order, which can be done in $\mathcal {O}(|{\varOmega }|\log (|{\varOmega }|))$ time. Defining $a_{(0)}:=0$ and $a_{(|{\varOmega }|+1)}:=\infty$, we then have for all $j\in \{0,1,\ldots ,|{\varOmega }|\}$ that

  $$\begin{aligned} \frac{\rho }{\rho +\theta }~a_{(j)} \le \frac{\xi }{\theta } \le \frac{\rho }{\rho +\theta }~a_{(j+1)} \Leftrightarrow \frac{1}{\xi }~a_{(j)}-\frac{1}{\rho } \le \frac{1}{\theta } \le \frac{1}{\xi }~a_{(j+1)}-\frac{1}{\rho }. \end{aligned}$$

  (50)

  Let $\bar{k}:=\max \left\{ j: a_{(j)}\le \frac{\xi }{\rho },\ 0\le j\le |{\varOmega }| \right\}$, and for all $\bar{k}< j\le |{\varOmega }|$ define $\theta _j:=\frac{1}{\frac{1}{\xi }~a_{(j)}-\frac{1}{\rho }}$. Then for all $\bar{k}< j\le |{\varOmega }|$, we have

  $$\begin{aligned} \phi (\theta _j)=\sqrt{\left( \frac{\rho }{\rho +\theta _j}\right) ^2~\sum _{i=0}^j a^2_{(i)}+(|{\varOmega }|-j)~\left( \frac{\xi }{\theta _j}\right) ^2}. \end{aligned}$$

  (51)

  Also define $\theta _{\bar{k}}:=\infty$ and $\theta _{|{\varOmega }|+1}:=0$ so that $\phi (\theta _{\bar{k}}):=0$ and $\phi (\theta _{|{\varOmega }|+1})=\phi (0)=\Vert A\Vert _F>\delta$. Note that $\{\theta _j\}_{\{\bar{k}< j\le |{\varOmega }|\}}$ contains all the points at which $\phi (\theta )$ may not be differentiable for $\theta \ge 0$. Define $j^*:=\max \{j:\ \phi (\theta _j)\le \delta ,\ \bar{k}\le j\le |{\varOmega }|\}$. Then $\theta ^*$ is the unique solution of the system

  $$\begin{aligned} \sqrt{\left( \frac{\rho }{\rho +\theta }\right) ^2~\sum _{i=0}^{j^*} a^2_{(i)}+(|{\varOmega }|-j^*)~\left( \frac{\xi }{\theta }\right) ^2}=\delta \,\hbox {and}\, \theta >0, \end{aligned}$$

  (52)

  since $\phi (\theta )$ is continuous and strictly decreasing in $\theta$ for $\theta \ge 0$. Solving the equation in (52) requires finding the roots of a fourth-order polynomial (also known as a quartic function). Lodovico Ferrari showed in 1540 that the roots of quartic functions can be solved in closed form. Thus, it follows that $\theta ^*>0$ can be computed in $\mathcal {O}(1)$ operations. Note that if $\bar{k}=|{\varOmega }|$, then $\theta ^*$ is the solution of the equation

  $$\begin{aligned} \sqrt{\left( \frac{\rho }{\rho +\theta ^*}\right) ^2~\sum _{i=1}^{|{\varOmega }|} a^2_{(i)}}=\delta , \end{aligned}$$

  (53)

  i.e. $\theta ^*= \rho \left( \frac{\Vert A\Vert _F}{\delta }-1\right) = \rho \left( \frac{\Vert \pi _{\varOmega }\left( D-q(\tilde{Z})\right) \Vert _F}{\delta }-1\right)$.

Hence, we have proved that problem $(P_{ns})$ can be solved efficiently when $\delta > 0$.

Now, suppose $\delta =0$. Since $\pi _{\varOmega }\left( Z^*+S^*-D\right) =0$, problem $(P_{ns})$ can be written as

$$\begin{aligned} \begin{array}{l@{\quad }l} \min _{Z,S\in \mathbb {R}^{m\times n}}&\xi \rho ^{-1} \Vert \pi _{\varOmega }(S)\Vert _1+\frac{1}{2} \Vert \pi _{\varOmega }\left( D-S-q(\tilde{Z})\right) +\pi _{{\varOmega }^c}\left( Z-q(\tilde{Z})\right) \Vert _F^2. \end{array}\nonumber \\ \end{aligned}$$

(54)

Then (13) and $Z^*=\pi _{\varOmega }\left( D-S^*\right) +\pi _{{\varOmega }^c}\left( q(\tilde{Z})\right)$ trivially follow from first-order optimality conditions for the above problem.

1.2 Proof of Lemma 2

Let $W^*:=-Q+\rho (\tilde{Z}-Z^*)$. Then (38) in the proof of Lemma 1 implies that $W^*=\theta ^*~\pi _{\varOmega }\left( Z^*+S^*-D\right)$. From the first-order optimality conditions of $(P_{ns})$ in (9), we have that $(W^*,-W)\in \partial \mathbf{1}_\chi (Z^*,S^*)$ for some $W\in \partial \xi \Vert S^*\Vert _1$. From (38) and (39), it follows that $-W^*\in \partial \xi \Vert S^*\Vert _1$. The definition of $\chi$, chain rule on subdifferential (see Theorem 23.9 in [26]), and $-W^*\in \partial \xi \Vert S^*\Vert _1$ together imply that $(W^*,W^*)\in \partial \mathbf{1}_\chi (Z^*,S^*)$.

1.3 Proof of Lemma 3

Since $L_{k+1}$ is the optimal solution to the subproblem in Step 4 of ADMIP corresponding to the $k$-th iteration, it follows that

$$\begin{aligned} 0\in \partial \Vert L_{k+1}\Vert _*+ Y_k+\rho _k(L_{k+1}-Z_k). \end{aligned}$$

(55)

Let $\theta _k\ge 0$ denote the optimal Lagrange multiplier for the quadratic constraint in Step 5 sub-problem in the $k$-th iteration. Since $(Z_{k+1},S_{k+1})$ is the optimal solution, the first-order optimality conditions imply that

$$\begin{aligned}&0\in \xi \partial \Vert S_{k+1}\Vert _1+ \theta _k~\pi _{\varOmega }\left( Z_{k+1}+S_{k+1}-D\right) , \end{aligned}$$

(56)

$$\begin{aligned}&-Y_k+\rho _k(Z_{k+1}-L_{k+1})+\theta _k~\pi _{\varOmega }\left( Z_{k+1}+S_{k+1}-D\right) =0. \end{aligned}$$

(57)

From (55), it follows that $-\hat{Y}_{k+1}\in \partial \Vert L_{k+1}\Vert _*$. From (56) and (57), it follows that $-Y_{k+1}\in \xi ~\partial \Vert S_{k+1}\Vert _1$. Since $\partial \Vert L\Vert _*$ and $\partial \Vert S\Vert _1$ are uniformly bounded sets for all $L, S\in \mathbb {R}^{m\times n}$, it follows that $\{\hat{Y}_k\}_{k\in \mathbb {Z}_+}$ and $\{Y_k\}_{k\in \mathbb {Z}_+}$ are bounded sequences. Moreover, (57) implies that $\pi _{\varOmega }\left( Y_k\right) =Y_k$ for all $k\ge 1$.

1.4 Proof of Lemma 4

For all $k \ge 0$, since $Y_{k+1}=Y_k+\rho _k(L_{k+1}-Z_{k+1})$ and and $\hat{Y}_{k+1}:=Y_k+\rho _k(L_{k+1}-Z_k)$, we have that $Y_{k+1}-\hat{Y}_{k+1}=\rho _k(Z_k-Z_{k+1})$. Using these relations, we obtain the following equality

$$\begin{aligned}&\rho _k^{-1}\langle Y_{k+1}-Y_k, Y_{k+1}-Y^* \rangle = \rho _k\langle L_{k+1}-L^*, Z_k-Z_{k+1} \rangle \nonumber \\&\quad +\,\langle L_{k+1}-L^*, \hat{Y}_{k+1}-Y^* \rangle +\langle L^*-Z_{k+1}, Y_{k+1}-Y^* \rangle . \end{aligned}$$

(58)

Moreover, we also have

$$\begin{aligned}&\Vert Z_{k+1}-L^*\Vert _F^2+\rho _{k}^{-2}\Vert Y_{k+1}-Y^*\Vert _F^2 \nonumber \\&\quad = \Vert Z_{k}-L^*\Vert _F^2+\rho _{k}^{-2}\Vert Y_{k}-Y^*\Vert _F^2-\Vert Z_{k+1}-Z_k\Vert _F^2-\rho _{k}^{-2}\Vert Y_{k+1}-Y_k\Vert _F^2 \nonumber \\&\qquad +\, 2\langle Z_{k+1}-L^*, Z_{k+1}-Z_k \rangle + 2 \rho _k^{-2} \langle Y_{k+1}-Y_k, Y_{k+1}-Y^* \rangle , \end{aligned}$$

(59)

$$\begin{aligned}&\quad = \Vert Z_{k}-L^*\Vert _F^2 + \rho _{k}^{-2}\Vert Y_{k}-Y^*\Vert _F^2-\Vert Z_{k+1}-Z_k\Vert _F^2 -\rho _{k}^{-2}\Vert Y_{k+1}-Y_k\Vert _F^2,\nonumber \\&\qquad +\,2\langle Z_{k+1}-L_{k+1}, Z_{k+1}-Z_k \rangle -\,2\rho _k^{-1}\langle -\hat{Y}_{k+1}+Y^*,L_{k+1}-L^* \rangle \nonumber \\&\qquad -\,2\rho _k^{-1}\langle -Y_{k+1}+Y^*, L^*-Z_{k+1} \rangle , \nonumber \\&\quad =\Vert Z_{k}-L^*\Vert _F^2 +\rho _{k}^{-2}\Vert Y_{k}-Y^*\Vert _F^2 -\Vert Z_{k+1}-Z_k\Vert _F^2-\rho _{k}^{-2}\Vert Y_{k+1}-Y_k\Vert _F^2, \nonumber \\&\qquad -\,2\rho _k^{-1}\left( \langle Y_{k+1}-Y_k, Z_{k+1}-Z_k \rangle + \langle -\hat{Y}_{k+1}+Y^*, L_{k+1}-L^* \rangle \right) \nonumber \\&\qquad -\,2\rho _k^{-1}\langle -Y_{k+1}+Y^*, L^*-Z_{k+1} \rangle , \end{aligned}$$

(60)

where the second equality follows from rewriting the last term in (59) using (58), and the last equality follows from the relation $L_{k+1}-Z_{k+1} = \rho _k^{-1}(Y_{k+1}-Y_k)$.

Since $Y^*$ and $\theta ^*$ are optimal Lagrangian dual variables, we have

$$\begin{aligned} (L^*,L^*,S^*)&=\mathop {\hbox {argmin}}\limits _{L,Z,S}\Vert L\Vert _*+\xi ~\Vert S\Vert _1 +\langle Y^*, L-Z \rangle \\&\qquad +\frac{\theta ^*}{2}\left( \Vert \pi _{\varOmega }\left( Z+S-D\right) \Vert ^2_F-\delta ^2\right) . \end{aligned}$$

From first-order optimality conditions, we get

$$\begin{aligned} 0\in & {} \partial \Vert L^*\Vert _*+Y^*,\\ 0\in & {} \xi ~\partial \Vert S^*\Vert _1+\theta ^*~\pi _{\varOmega }\left( L^*+S^*-D\right) ,\\ 0= & {} -Y^*+\theta ^*~\pi _{\varOmega }\left( L^*+S^*-D\right) . \end{aligned}$$

Hence, $-Y^*\in \partial \Vert L^*\Vert _*$ and $-Y^*\in \xi ~\partial \Vert S^*\Vert _1$. Moreover, from Lemma 3, we also have that $-Y_k\in \partial \xi ~\Vert S_k\Vert _1$ for all $k\ge 1$. Since $\xi ~\Vert .\Vert _1$ is convex, it follows that

$$\begin{aligned} \langle -Y_{k+1}+Y_k, S_{k+1}-S_k \rangle \ge 0, \end{aligned}$$

(61)

$$\begin{aligned} \langle -Y_{k+1}+Y^*, S_{k+1}-S^* \rangle \ge 0. \end{aligned}$$

(62)

Since $\rho _{k+1}\ge \rho _k$ for all $k\ge 1$, first adding (61) to (60), then adding and subtracting (62), we get

$$\begin{aligned}&\Vert Z_{k+1}-L^*\Vert _F^2 +\rho _{k+1}^{-2}\Vert Y_{k+1}-Y^*\Vert _F^2 \nonumber \\&\quad \le \Vert Z_{k}-L^*\Vert _F^2 +\rho _{k}^{-2}\Vert Y_{k}-Y^*\Vert _F^2 -\Vert Z_{k+1}-Z_k\Vert _F^2-\rho _{k}^{-2}\Vert Y_{k+1}-Y_k\Vert _F^2 \nonumber \\&\qquad -\,2\rho _k^{-1}\left( \langle -\hat{Y}_{k+1}+Y^*, L_{k+1}-L^* \rangle +\langle -Y_{k+1}+Y^*, S_{k+1}-S^* \rangle \right) \nonumber \\&\qquad -\,2\rho _k^{-1}\langle Y_{k+1}-Y_k,Z_{k+1}+S_{k+1}-Z_k-S_k \rangle \nonumber \\&\qquad -\,2\rho _k^{-1}\langle -Y_{k+1}+Y^*,L^*+S^*-Z_{k+1}-S_{k+1} \rangle . \end{aligned}$$

(63)

Lemma 2 applied to the Step 5 sub-problem corresponding to the $k$-th iteration gives $(Y_{k+1},Y_{k+1})\in \partial \mathbf{1}_{\chi }(Z_{k+1},S_{k+1})$. Using an argument similar to that used in the proof of Lemma 2, one can also show that $(Y^*,Y^*)\in \partial \mathbf{1}_{\chi }(L^*,S^*)$. Moreover, since $-Y^*\in \partial \xi ~\Vert S^*\Vert _1$, $-Y^*\in \partial \Vert L^*\Vert _*$, and $-Y_{k}\in \partial \xi ~\Vert S_k\Vert _1$, $-\hat{Y}_{k}\in \partial \Vert L_k\Vert _*$ for all $k\ge 1$, we have that for all $k \ge 0$,

$$\begin{aligned} \langle Y_{k+1}-Y_k, Z_{k+1}+S_{k+1}-Z_k-S_k \rangle \ge 0,\\ \langle -Y_{k+1}+Y^*, L^*+S^*-Z_{k+1}-S_{k+1} \rangle \ge 0,\\ \langle -Y_{k+1}+Y^*, S_{k+1}-S^* \rangle \ge 0,\\ \langle -\hat{Y}_{k+1}+Y^*, L_{k+1}-L^* \rangle \ge 0. \end{aligned}$$

This set of inequalities and (63) together imply that $\{\Vert Z_{k}-L^*\Vert _F^2+\rho _{k}^{-2}\Vert Y_{k}-Y^*\Vert _F^2\}_{k\in \mathbb {Z}_+}$ is a non-increasing sequence. Using this fact, rewriting (63) and summing over $k\in \mathbb {Z}_+$, we get

$$\begin{aligned}&\sum _{k\in \mathbb {Z}_+}\Vert Z_{k+1}-Z_k\Vert _F^2+\rho _{k}^{-2}\Vert Y_{k+1}-Y_k\Vert _F^2 \\&\qquad +\, 2\sum _{k\in \mathbb {Z}_+}\rho _k^{-1}\left( \langle -\hat{Y}_{k+1}+Y^*, L_{k+1}-L^* \rangle +\langle -Y_{k+1}+Y^*, S_{k+1}-S^* \rangle \right) \\&\qquad +\, 2\sum _{k\in \mathbb {Z}_+}\rho _k^{-1}\langle Y_{k+1}-Y_k,Z_{k+1}+S_{k+1}-Z_k-S_k \rangle \\&\qquad +\, 2\sum _{k\in \mathbb {Z}_+}\rho _k^{-1}\langle -Y_{k+1}+Y^*,L^*+S^*-Z_{k+1}-S_{k+1} \rangle \\&\quad \le \sum _{k\in \mathbb {Z}_+}\left( \Vert Z_{k}-L^*\Vert _F^2 +\rho _{k}^{-2}\Vert Y_{k}-Y^*\Vert _F^2-\Vert Z_{k+1}-L^*\Vert _F^2\right. \\&\qquad \left. -\,\rho _{k+1}^{-2}\Vert Y_{k+1}-Y^*\Vert _F^2\right) <\infty . \end{aligned}$$

This inequality is sufficient to prove the rest of the lemma.