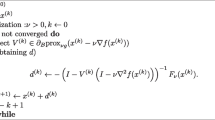Skip to main content
SpringerLink
Log in

Proximal methods for the latent group lasso penalty

  • Published:
Computational Optimization and Applications Aims and scope Submit manuscript

Abstract

We consider a regularized least squares problem, with regularization by structured sparsity-inducing norms, which extend the usual ℓ 1 and the group lasso penalty, by allowing the subsets to overlap. Such regularizations lead to nonsmooth problems that are difficult to optimize, and we propose in this paper a suitable version of an accelerated proximal method to solve them. We prove convergence of a nested procedure, obtained composing an accelerated proximal method with an inner algorithm for computing the proximity operator. By exploiting the geometrical properties of the penalty, we devise a new active set strategy, thanks to which the inner iteration is relatively fast, thus guaranteeing good computational performances of the overall algorithm. Our approach allows to deal with high dimensional problems without pre-processing for dimensionality reduction, leading to better computational and prediction performances with respect to the state-of-the art methods, as shown empirically both on toy and real data.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Algorithm 1
Algorithm 2
Algorithm 3
Algorithm 4
Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Notes

  1. It is the solution computed via the projected Newton method for the dual problem with very tight tolerance

References

  1. Bach, F.: Consistency of the group lasso and multiple kernel learning. J. Mach. Learn. Res. 9, 1179–1225 (2008)

    MATH  MathSciNet  Google Scholar 

  2. Bach, F.R., Lanckriet, G., Jordan, M.I.: Multiple kernel learning, conic duality, and the smo algorithm. In: ICML. ACM International Conference Proceeding Series, vol. 69 (2004)

    Google Scholar 

  3. Bach, F., Jenatton, R., Mairal, J., Obozinski, G.: Optimization with sparsity-inducing penalties. Found. Trends Mach. Learn. 4(1), 1–106 (2012)

    Article  Google Scholar 

  4. Bauschke, H.: The approximation of fixed points of compositions of nonexpansive mappings in Hilbert space. J. Math. Anal. Appl. 202(1), 150–159 (1994)

    Article  MathSciNet  Google Scholar 

  5. Bauschke, H., Combettes, P.L.: Convex Analysis and Monotone Operator Theory in Hilbert Spaces. Springer, New York (2011)

    Book  MATH  Google Scholar 

  6. Beck, A., Teboulle, M.: A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2(1), 183–202 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  7. Becker, S., Bobin, J., Candes, E.: NESTA: A fast and accurate first-order method for sparse recovery. SIAM J. Imaging Sci. 4(1), 1–39 (2009)

    Article  MathSciNet  Google Scholar 

  8. Bertsekas, D.: Projected Newton methods for optimization problems with simple constraints. SIAM J. Control Optim. 20(2), 221–246 (1982)

    Article  MATH  MathSciNet  Google Scholar 

  9. Boyle, J., Dykstra, R.: A method for finding projections onto the intersection of convex sets in Hilbert spaces. In: Dykstra, R., Robertson, T., Wright, F. (eds.) Advances in Order Restricted Statistical Inference. Lecture Notes in Statistics, vol. 37, pp. 28–48. Springer, Berlin (1985)

    Chapter  Google Scholar 

  10. Brayton, R., Cullum, J.: An algorithm for minimizing a differentiable function subject to box constraints and errors. J. Optim. Theory Appl. 29, 521–558 (1979)

    Article  MATH  MathSciNet  Google Scholar 

  11. Chambolle, A., Pock, T.: A first-order primal-dual algorithm for convex problems with applications to imaging. J. Math. Imaging Vis. 40(1), 120–145 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  12. Chen, S., Donoho, D., Saunders, M.: Atomic decomposition by basis pursuit. SIAM J. Sci. Comput. 20(1), 33–61 (1999)

    MATH  MathSciNet  Google Scholar 

  13. Chen, X., Lin, Q., Kim, S., Carbonell, J., Xing, E.P.: Smoothing proximal gradient method for general structured sparse regression. Ann. Appl. Stat. 6(2), 719–752 (2012)

    Article  MathSciNet  Google Scholar 

  14. Combettes, P.L., Wajs, V.R.: Signal recovery by proximal forward-backward splitting. Multiscale Model. Simul. 4(4), 1168–1200 (2005) (electronic)

    Article  MATH  MathSciNet  Google Scholar 

  15. Deng, W., Yin, W., Zhang, Y.: Group sparse optimization by alternating direction method (2011)

  16. Duchi, J., Singer, Y.: Efficient online and batch learning using forward backward splitting. J. Mach. Learn. Res. 10, 2899–2934 (2009)

    MATH  MathSciNet  Google Scholar 

  17. Efron, B., Hastie, T., Johnstone, I., Tibshirani, R.: Least angle regression. Ann. Stat. 32, 407–499 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  18. Fornasier, M. (ed.): Theoretical Foundations and Numerical Methods for Sparse Recovery. Radon Series on Computational and Applied Mathematics, vol. 9. de Gruyter, Berlin (2010)

    MATH  Google Scholar 

  19. Fornasier, M., Daubechies, I., Loris, I.: Accelerated projected gradient methods for linear inverse problems with sparsity constraints. J. Fourier Anal. Appl. (2008)

  20. Hale, E.T., Yin, W., Zhang, Y.: Fixed-point continuation for l1-minimization: methodology and convergence. SIAM J. Optim. 19(3), 1107–1130 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  21. Jacob, L., Obozinski, G., Vert, J.-P.: Group lasso with overlap and graph lasso. In: Proceedings of the 26th International Annual Conference on Machine Learning, pp. 433–440 (2009)

    Google Scholar 

  22. Jacques, L., Hammond, D., Fadili, J.: Dequantizing compressed sensing: when oversampling and non-Gaussian constraints combine. IEEE Trans. Inf. Theory 57(1), 559–571 (2011)

    Article  MathSciNet  Google Scholar 

  23. Jenatton, R., Audibert, J.-Y., Bach, F.: Structured variable selection with sparsity-inducing norms. Technical report, INRIA (2009)

  24. Jenatton, R., Obozinski, G., Bach, F.: Structured principal component analysis. In: Proceedings of the 13 International Conference on Artificial Intelligence and Statistics (2010)

    Google Scholar 

  25. Liu, J., He, J.: Fast overlapping group lasso (2010)

  26. Mairal, J., Jenatton, R., Obozinski, G., Bach, F.: Network flow algorithms for structured sparsity. Adv. Neural Inf. Process. Syst. (2010)

  27. Meier, L., van de Geer, S., Buhlmann, P.: The group lasso for logistic regression. J. R. Stat. Soc. B 70, 53–71 (2008)

    Article  MATH  Google Scholar 

  28. Micchelli, C.A., Pontil, M.: Learning the kernel function via regularization. J. Mach. Learn. Res. 6, 1099–1125 (2005)

    MATH  MathSciNet  Google Scholar 

  29. Moreau, J.-J.: Fonctions convexes duales et points proximaux dans un espace hilbertien. C. R. Acad. Sci. Paris 255, 2897–2899 (1962)

    MATH  MathSciNet  Google Scholar 

  30. Mosci, S., Rosasco, L., Santoro, M., Verri, A., Villa, S.: Solving structured sparsity regularization with proximal methods. In: Balcázar, J., Bonchi, F., Gionis, A., Sebag, M. (eds.) Machine Learning and Knowledge Discovery in Databases. Lecture Notes in Computer Science, vol. 6322, pp. 418–433. Springer, Berlin (2010)

    Chapter  Google Scholar 

  31. Mosci, S., Villa, S., Verri, A., Rosasco, L.: A primal-dual algorithm for group sparse regularization with overlapping groups. In: Lafferty, J., Williams, C.K.I., Shawe-Taylor, J., Zemel, R.S., Culotta, A. (eds.) Advances in Neural Information Processing Systems, vol. 23, pp. 2604–2612 (2010)

    Google Scholar 

  32. Nesterov, Y.: A method for unconstrained convex minimization problem with the rate of convergence o(1/k 2). Dokl. Akad. Nauk SSSR 269(3), 543–547 (1983)

    MathSciNet  Google Scholar 

  33. Nesterov, Y.: Smooth minimization of non-smooth functions. Math. Program., Ser. A 103(1), 127–152 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  34. Nesterov, Y.: Gradient methods for minimizing composite objective function. CORE Discussion Paper 2007/76, Catholic University of Louvain, September 2007

  35. Obozinski, G., Jacob, L., Vert, J.-P.: Group lasso with overlaps: the latent group lasso approach. Research report, October 2011

  36. Park, M.Y., Hastie, T.: L1-regularization path algorithm for generalized linear models. J. R. Stat. Soc. B 69, 659–677 (2007)

    Article  MathSciNet  Google Scholar 

  37. Peyré, G., Fadili, J.: Group sparsity with overlapping partition functions. In: Proc. EUSIPCO 2011, pp. 303–307 (2011)

    Google Scholar 

  38. Poliak, E.: Computational Methods in Optimization: A Unified Approach. Academic Press, New York (1971)

    Google Scholar 

  39. Qin, Z., Goldfarb, D.: Structured sparsity via alternating direction methods. J. Mach. Learn. Res. 13, 1435–1468 (2012)

    MATH  MathSciNet  Google Scholar 

  40. Qin, Z., Scheinberg, K., Goldfarb, D.: Efficient block-coordinate descent algorithms for the group lasso (2012)

  41. Rockafellar, R.T.: Monotone operators and the proximal point algorithm. SIAM J. Control Optim. 14(5), 877–898 (1976)

    Article  MATH  MathSciNet  Google Scholar 

  42. Rosasco, L., Mosci, M., Santoro, S., Verri, A., Villa, S.: Iterative projection methods for structured sparsity regularization. Technical Report MIT-CSAIL-TR-2009-050, MIT (2009)

  43. Rosen, J.: The gradient projection method for nonlinear programming, part I: Linear constraints. J. Soc. Ind. Appl. Math. 8, 181–217 (1960)

    Article  MATH  Google Scholar 

  44. Roth, V., Fischer, B.: The group-lasso for generalized linear models: uniqueness of solutions and efficient. In: Proceedings of 25th ICML (2008)

    Google Scholar 

  45. Salzo, S., Villa, S.: Accelerated and inexact proximal point algorithms. J. Convex Anal. 9(4), 1167–1192 (2012)

    MathSciNet  Google Scholar 

  46. Schmidt, M., Le Roux, N., Bach, F.: Convergence rates of inexact proximal-gradient methods for convex optimization. In: Advances in Neural Information Processing Systems (NIPS) (2011)

    Google Scholar 

  47. Subramanian, A., et al.: Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proc. Natl. Acad. Sci. USA 102(43), 15545–15550 (2005)

    Article  Google Scholar 

  48. The Gene Ontology Consortium: Gene ontology: tool for the unification biology. Nat. Genet. 25, 25–29 (2000)

    Article  Google Scholar 

  49. Tibshirani, R.: Regression shrinkage and selection via the lasso. J. R. Stat. Soc. B 58(1), 267–288 (1996)

    MATH  MathSciNet  Google Scholar 

  50. Tseng, P.: Approximation accuracy, gradient methods, and error bound for structured convex optimization. Math. Program., Ser. B 125(2), 263–295 (2010)

    Article  MATH  Google Scholar 

  51. van ’t Veer, L., et al.: Gene expression profiling predicts clinical outcome of breast cancer. Nature 415(6871), 530 (2002)

    Article  Google Scholar 

  52. Villa, S., Salzo, S., Baldassarre, L., Verri, A.: Accelerated and inexact forward-backward algorithms. SIAM J. Optim. 23(3), 1607–1633 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  53. Yuan, M., Lin, Y.: Model selection and estimation in regression with grouped variables. J. R. Stat. Soc. B 68(1), 49–67 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  54. Zhao, P., Rocha, G., Yu, B.: The composite absolute penalties family for grouped and hierarchical variable selection. Ann. Stat. 37(6A), 3468–3497 (2009)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors wish to thank Saverio Salzo for carefully reading the paper. This material is based upon work partially supported by the FIRB Project RBFR12M3AC “Learning meets time: a new computational approach for learning in dynamic systems” and the Center for Minds, Brains and Machines (CBMM), funded by NSF STC award CCF-1231216.

Author information

Authors and Affiliations

  1. Laboratory for Computational and Statistical Learning, Istituto Italiano di Tecnologia, Genoa, Italy

    Silvia Villa & Lorenzo Rosasco

  2. Massachussets Institute of Technology, Cambridge, USA

    Lorenzo Rosasco

  3. DIBRIS, Università di Genova, Genoa, Italy

    Lorenzo Rosasco, Sofia Mosci & Alessandro Verri

Authors
  1. Silvia Villa
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lorenzo Rosasco
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sofia Mosci
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Alessandro Verri
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Silvia Villa.

Appendix: Projected Newton method

Appendix: Projected Newton method

In this appendix we report as Algorithm 5 Bertsekas’ projected Newton method described in [8], with the modifications needed to perform maximization instead of minimization of a function.

Algorithm 5
figure 9

Projection onto \(K_{2}^{\mathcal{G}}\)

Full size image

The step size rule, i.e. the choice of α, is a combination of the Armijo-like rule [43] and the Armijo rule usually employed in unconstrained minimization (see, e.g., [38]).

Rights and permissions

Reprints and permissions

About this article

Cite this article

Villa, S., Rosasco, L., Mosci, S. et al. Proximal methods for the latent group lasso penalty. Comput Optim Appl 58, 381–407 (2014). https://doi.org/10.1007/s10589-013-9628-6

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10589-013-9628-6

Keywords

Search

Navigation