Skip to main content
SpringerLink
Log in

Detecting “dense” columns in interior point methods for linear programs

  • Published:
Computational Optimization and Applications Aims and scope Submit manuscript

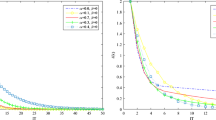
Abstract

During the iterations of interior point methods symmetric indefinite systems are decomposed by LD̂L T factorization. This step can be performed in a special way where the symmetric indefinite system is transformed to a positive definite one, called the normal equations system. This approach proved to be efficient in most of the cases and numerically reliable, due to the positive definite property. It has been recognized, however, that in case the linear program contains “dense” columns, this approach results in an undesirable fill–in during the computations and the direct factorization of the symmetric indefinite system is more advantageous. The paper describes a new approach to detect cases where the system of normal equations is not preferable for interior point methods and presents a new algorithm for detecting the set of columns which is responsible for the excessive fill–in in the matrix AA T. By solving large–scale linear programming problems we demonstrate that our heuristic is reliable in practice.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. R.P. Amestoy, T.A. Davis, and I.S. Duff, “An approximate minimum degree ordering algorithm,” SIAM Journal on Matrix Analysis and Applications, vol. 17, no. 4, pp. 886–905, 1996.

    Article  MATH  MathSciNet  Google Scholar 

  2. E.D. Andersen, J. Gondzio, C. Mészáros, and X. Xu, “Implementation of interior point methods for large scale linear programs,” in Interior Point Methods of Mathematical Programming, T. Terlaky (Ed.), Kluwer Academic Publishers, 1996, pp. 189–252.

  3. J.R. Bunch and B.N. Parlett, “Direct methods for solving symmetric indefinit systems of linear equations,” SIAM Journal on Numerical Analysis, vol. 8, pp. 639–655, 1971.

    Article  MathSciNet  Google Scholar 

  4. I.S. Duff, N.I.M. Gould, J.K. Reid, J.A. Scott, and K. Turner, “The factorization of sparse symmetric indefinite matrices,” IMA J. Numer. Anal. vol. 11, pp. 181–204, 1991.

    Article  MATH  MathSciNet  Google Scholar 

  5. R. Fourer and S. Mehrotra, “Solving symmetric indefinite systems in an interior point method for linear programming,” Mathematical Programming, vol. 62, pp. 15–40, 1993.

    Article  MathSciNet  Google Scholar 

  6. D. Goldfarb and K. Scheinberg, “A product-form Cholesky factorization method for handling dense columns in interior point methods for linear programming,” Mathematical Programming, vol. 99, no. 1, pp. 1–34, 2004.

    Article  MATH  MathSciNet  Google Scholar 

  7. J. Gondzio, “Multiple centrality corrections in a primal-dual method for linear programming,” Computational Optimization and Applications, vol. 6, no. 137–156, 1996.

  8. N.K. Karmarkar, “A polynomial-time algorithm for linear programming,” Combinatorica, vol. 4, pp. 373–395, 1984.

    Article  MATH  MathSciNet  Google Scholar 

  9. I.J. Lustig, R.E. Marsten, and D.F. Shanno, “The interaction of algorithms and architectures for interior point methods,” in Advances in Optimization and Parallel Computing, P.M. Pardalos (Ed.), Elsevier Sciences Publishers B.V. 1992, pp. 190–205.

  10. I.J. Lustig and E. Rothberg, “Gigaflops in linear programming,” Operations Research Letters, vol. 18, no. 4, pp. 157–165, 1996.

    Article  MATH  MathSciNet  Google Scholar 

  11. I. Maros and C. Mészáros, “The role of the augmented system in interior point methods,” European Journal on Operational Research, vol. 107, no. 3, pp. 720–736, 1998.

    Article  MATH  Google Scholar 

  12. C. Mészáros, “Fast Cholesky factorization for interior point methods of linear programming,” Computers & Mathematics with Applications, vol. 31, nos. (4/5), pp. 49–54, 1996.

    Article  MATH  Google Scholar 

  13. C. Mészáros, “On free variables in interior point methods,” Optimization Methods and Software, vol. 9, pp. 121–139, 1997.

    Google Scholar 

  14. C. Mészáros, “On the sparsity issues of interior point methods for quadratic programming,” Working paper WP 98-4, Computer and Automation Institute, Hungarian Academy of Sciences, Budapest, 1998.

  15. C. Mészáros, “The BPMPD interior-point solver for convex quadratic problems,” Optimization Methods and Software, vol. 11/12, pp. 431–449, 1999.

    Google Scholar 

  16. C. Mészáros, “On the Cholesky factorization in interior point methods,” Computers & Mathematics with Applications, vol. 50, pp. 1157–1166, 2005.

    Article  MATH  MathSciNet  Google Scholar 

  17. C. Mészáros, “On the numerical issues of interior point methods,” Working paper WP 2005-3, Computer and Automation Institute, Hungarian Academy of Sciences, Budapest, 2005.

  18. C. Mészáros, “On the performance of the Cholesky factorization in interior point methods on Pentium 4 processors,” CEJOR, vol. 13, no. 4, pp. 289–298, 2005.

    MATH  Google Scholar 

  19. C. Mészáros and U.H. Suhl, “Advanced preprocessing techniques for linear and quadratic programming,” OR Spectrum, vol. 25, pp. 575–595, 2004.

    Article  Google Scholar 

  20. H.D. Mittelmann, “Benchmarking Interior Point LP/QP Solvers,” Optimization Methods and Software, vol. 12, pp. 655–670, 1999.

    MathSciNet  Google Scholar 

  21. H.D. Mittelmann and P. Spellucci, “Decision tree for optimization software,” World Wide Web, http://plato.la.asu.edu/guide.html, 1998.

  22. C Roos, T. Terlaky, and J.-Ph. Vial, Theory and Algorithms for Linear Optimization: An Interior Point Approach. John Wiley & Sons, 1996.

  23. R.J. Vanderbei, “Symmetric quasi-definite matrices,” SIAM Journal on Optimization, vol. 5, no. 1, pp. 100–113, 1995.

    Article  MATH  MathSciNet  Google Scholar 

  24. R.J. Vanderbei and T.J. Carpenter, “Symmetric indefinite systems for interior point methods,” Mathematical Programming, vol. 58, pp. 1–32, 1993.

    Article  MATH  MathSciNet  Google Scholar 

  25. M.H. Wright, “Some properties of the Hessian of the logarithmic barrier function,” Mathematical Programming, vol. 67, pp. 265–295, 1994.

    Article  MathSciNet  Google Scholar 

  26. S.J. Wright, Primal–dual interior point methods. SIAM, T57.74.W75, University Science Center, Philadelphia, 1997.

  27. S.J. Wright, “Stability of linear algebra computations in interior-point methods for linear programming,” SIAM Journal on Matrix Analysis and Applications, vol. 18, pp. 191–222, 1997.

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Laboratory of Operations Research and Decision Systems, Computer and Automation Research Institute, Hungarian Academy of Sciences, Lagym´nyosi u. 11, H-1111, Budapest, Hungary

    Csaba Mészáros

Authors
  1. Csaba Mészáros
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Csaba Mészáros.

Additional information

This work was supported in part by the Hungarian Scientific Research Fund OTKA K60480.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Mészáros, C. Detecting “dense” columns in interior point methods for linear programs. Comput Optim Appl 36, 309–320 (2007). https://doi.org/10.1007/s10589-006-9008-6

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10589-006-9008-6

Keywords

Search

Navigation