Shear modulus of single wood pulp fibers from torsion tests

Abstract

The shear modulus of pulp fibers is difficult to measure and only very little literature is available on this topic. In this work we are introducing a method to measure this fiber property utilizing a custom built instrument. From the geometry of the fiber cross section, the fiber twisting angle and the applied torque, the shear modulus is derived by de Saint Venant’s theory of torsion. The deformation of the fiber is applied by a moving coil mechanism. The support of the rotating part consists of taut bands, making it nearly frictionless, which allows easy control of the torque to twist the fiber. A permanent magnet moving coil meter was fitted with a sample holder for fibers and torque references. Measurements on fine metal bands were performed to validate the instrument. The irregular shape of the fibers was reconstructed from several microtome cuts and an apparent torsion constant was computed by applying de Saint Venant’s torsion theory. Fibers from two types of industrial pulp were measured: thermomechanical pulp (TMP) and Kraft pulp. The average shear modulus was determined as (2.13 ${\pm }$ 0.36) GPa for TMP and (2.51 ${\pm }$ 0.50) GPa for Kraft fibers, respectively. The TMP fibers showed a smaller shear modulus but, due to their less collapsed state, a higher torsional rigidity than the kraft fibers.

Introduction

To understand and predict the mechanical properties of paper sheets, large scale simulations of fiber networks are performed. In such models, the fiber is the principal constituent, the fibrilar structure of the fiber is not considered, as multiscale models would only allow the simulation of a small patch of the sheet. To each fiber in the simulated network, properties are ascribed such as the geometry of the fiber, its spatial orientation, the connection to other fibers in the network and its mechanical properties. The fibers can be modeled consisting of a transverse isotropic material. Some parameters, like the longitudinal modulus of elasticity, are subject of many studies, e. g. (Jayne 1959; Derek 1983; Jajcinovic et al. 2016). Other parameters, like the longitudinal shear modulus, are not well-established. In network simulations, such unknown parameters are fitted by adapting the models to show the behavior of real paper sheets. The parameters found in this way are then checked against estimates of these parameters, if available, or against theoretical predictions.

Fig. 1

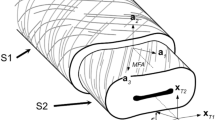
Illustration of the shear deformation of an element in an idealized fiber under torsion. Please note that for evaluation of the torsional constant and the fiber shear modulus the true fiber cross sectional shape was analyzed, compare Fig. 5 and Sect. "Determining the Torsion Constant of the Fiber"

Very little work has been devoted to direct measurement of the shear modulus on pulp fibers (Kolseth and Alf 1983). This is partly due to the apparent difficulties of this measurement. Also, until recent years, the shear modulus was of little practical use, only with the advent of comprehensive fiber network simulations (Kulachenko and Uesaka 2012; Li et al. 2018) the need to determine the fiber shear modulus has increased. Particularly for modeling fiber networks exposed to a high shear load, e.g. creasing and folding of paper and board, the fiber shear modulus becomes a relevant material parameter.

In this work we will determine the longitudinal shear modulus of the pulp fiber wall from torsion experiments on fibers. Figure 1 gives a sketch of an idealized fiber under torsional load with the torsional shear stress $\tau$ drawn in the fiber cross section. This torsional shear is deforming elements of the fiber wall, inducing a shear deformation indicted by the angle $\gamma$ in Fig. 1. In terms of mechanics the shear modulus determining this deformation is called the longitudinal shear modulus. In this work we will stick to this terminology, thus we are measuring the longitudinal shear modulus of the fibers.

Related Work Torsional experiments were conducted by Kolseth and Alf (1983) to determine the longitudinal shear modulus of kraft pulp fibers. His instrument featured a rotary table as actuator and a rotating coil suspended in a uniform magnetic field to compensate the torque of the twisted fiber. Great care was taken to align the fiber with the axis of rotation. Kolseth twisted the fibers until they ruptured after about three turns of the rotary table and simultaneously recorded the torque applied to the fiber. The loading curve clearly showed a nonlinear twist-torque relationship. Despite that, Kolseth used the breaking load to calculate the shear modulus. He used a simple approximation of the torsion constant. For each of the tested fibers, a single cross section was acquired. All of the fibers had an uncollapsed lumen, therefore the cross sections had a hole. Kolseth transformed the fiber cross sections into an annulus of the same cross-sectional area with an inner ring of the same area as the hole in the cross section. The torsion constant of the annulus was then used to calculate the shear modulus. As circular cross sections have the largest torsion constant for a given cross-sectional area, this approximation over-estimates the torsion constant of the fiber cross section (Pólya 1948). The application of the torsion theory for thin-walled tubes would have approximated the torsion constant of these fibers much better (Sokolnikoff 1956; Szabó 1961). While the principal design of this setup (i.e. measuring the torque while twisting the fiber) is elegant, we believe that two points need considerable improvement. First, the measured shear modulus highly depends on the shape of the fiber cross section. Measuring several cross sections of the same fiber reduces the noise considerably, also the true cross sectional shape of the fiber should be used instead of the apparent shape (Lorbach et al. 2012) or an approximated shape. Second the fiber shear modulus should be measured in the linear deformation regime and not from the torque at rupture. Finally, more fibers should be measured to obtain statistically meaningful results.

To determine the torsional properties of fibers torsion pendulums were also used. Naito et al. (July 1980) determined only torsional rigidity of kraft pulp fibers. They determined for red pine early wood kraft pulp fibers $w_{\mathrm {T}} \approx {30} \,\hbox {pNm}^{2}$ and for late wood $w_{\mathrm {T}} \approx {43} \,\hbox {pNm}^{2}$. Neither microtome cuts nor fiber compaction was performed. Without cross-sectional data available, the shear modulus could not be obtained. For fibers of uniform diameter, the longitudinal shear modulus was successfully determined by Tsai and Daniel (1999). For textile fibers, extensive measurements of the elastic properties were performed. An example of a comprehensive early study is (Meredith July 1954). He used analytical solutions of the torsion problem for fiber cross sections that were well approximated by simple geometrical shapes and a soap-film analogy for irregular cross sections (Sokolnikoff 1956).

In his thesis (Kolseth 1983) also used a torsional pendulum to determine the shear modulus for kraft pulp fibers. His instrument possessed a climate chamber with control of temperature and humidity. He used this instrument mainly to study the dependency of torsional rigidity on temperature (Kolseth et al. 1983). For a small set of kraft wood pulp fibers, the shear modulus was also determined. For this experiment Kolseth applied the theory of thin-walled tubes. But still only one cross section per fiber was evaluated. With this setup, he obtained a shear modulus of $G = {(3.6\ {\pm }\ 1.3)}$ GPa.

Fig. 2

Fiber sample (d) mounted in the instrument. The sample holder consists of a static rotation constraint (a) and a rotating cross beam (b) attached to the pointer (c) of the permanent magnet moving coil meter

A mechanism with a rotating coil in a radial uniform magnetic field was used by Dai et al. (2015) to determine the shear modulus of metallic glass fibers. In addition to the rotating coil mechanism used as actuator and sensor, an additional angular transducer allowed the torque measurement for arbitrary angles. The instrument had slide bearings for the spindle of the rotating coil. This allows for tight mechanical coupling of the axis of the instrument with the sample but introduces friction into the torque balance. The instrument measures torques in the range of 1 mN m with a resolution of 30 nN m. Huan et al. (2014) used the same instrument to measure thin copper wires. Instead of an angular transducer, a laser displacement sensor was used to measure the rotation angle. This limits the angular range but allows a better angular resolution. The glass fibers and the copper wires both had a circular cross section. The measurement of the diameter at three different positions was sufficient to determine the torsion constant.

Liu et al. (2016) used a torsion-balance to measure the torsional properties of single micron-diameter wires. The instrument used a rotary table as actuator. The sample and a torsion wire were glued together with a cross beam marking the joint. The prepared sample was mounted above the rotary table. The torque was introduced into the sample by a twisting head on the table. While the sample was twisted, the displacement of the cross beam was measured with a laser displacement sensor. The torsion wires were calibrated by a torsion pendulum. This design of the sample assembly looks promising for the application to natural fibers.

In conclusion, while there are some methods available to measure torsional rigidity of thin wires or fibers, no reliable data or method on the shear modulus of pulp fibers could be found in the literature. In order to obtain these data it is necessary to combine a measurement of fiber torsional rigidity with a reliable measurement of the fiber cross sectional shape, and to apply adequate mechanical modeling of the fiber twisting to evaluate the shear modulus.

Materials and methods

Design of the instrument

We adapted a permanent magnet moving coil instrument (PMMC) (Golding and Widdis 1963; Paul 1978; Stanek 1961) as actuator and sensor. PMMCs were used for sensitive and precise electrical measuring instruments until the technology was superseded by modern electronic instruments in the 1980s. In a PMMC, a coil rotates in a small circular gap between two pole pieces of a permanent magnet and a soft iron cylinder. The magnetic field in the gap is radial uniform and always perpendicular to the direction of movement of the coil. The torque induced is thus only dependent on the current through the coil but not on the angle of deflection. The strength of the magnetic field is determined by the geometry of the gap and the strength of the permanent magnet, neither change during the test. We only have to control and measure the electric current through the coil.

In a PMMC, the torque of the moving coil acts against a restoring spring. The restoring torque of the spring is proportional to the deflection of the coil, the deflection is thus proportional to the current in the coil. The deflection of the coil is indicated by a pointer on a scale. For the most sensitive of these instruments, the friction of pivot bearings is no longer acceptable. In these instruments the coils are supported by taut bands (Christoph 1951; Samal 1955) that act as bearings and as restoring springs. Taut bands are thin wires rolled down to a rectangular cross section. A rectangular cross section has a lower torsional rigidity than the circular cross section of the same area (Samal 1955; Pólya 1948), which allows taut bands to carry heavier moving systems without sacrificing sensitivity.

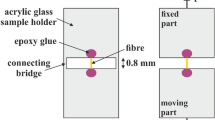
We adapted the PMMC of an analog handheld multimeter, Metrawatt Unigor 4p, that features a moving system with taut band suspension and a low 10 $\mu \text {A}$ current range. As a handheld instrument, the readings of the instrument are independent of the orientation of the instrument. The moving coil assembly together with the scale plate Dwere removed from the multimeter and placed on a separate mount. A beam was attached to the pointer that allowed for the sample to hang down from the beam centered over the axis of rotation of the PMMC. The design is shown in Fig. 2. The tension of the taut band was sufficient to keep the axis of rotation vertical, despite the torque introduced by the additional weight on the pointer. A fork shaped rotation constraint attached to the static part of the instrument prevented the rotation of the sample but allowed free movement otherwise. The necessary clearance between the restraint and the sample holder of 0.1 mm introduced a small slack, less than 2${^{\circ }}$, between the deflection of the pointer and the twisting deformation of the sample. The adjustment of the beam, so that the center of rotation was centered over the taut bands of the instrument, was performed using a telecentric lens.

A sample holder was designed to allow the easy insertion and removal of the samples from the instrument. The sample holder features a small piece of board to bring the sample in a vertical position centered over the axis of rotation of the PMMC. Also the board provides a small axial load on the samples to avoid buckling. See Fig. 3ii.

Fig. 3

Schematic representation of a torque reference (i) and a fiber sample (ii) mounted in the instrument. Both fit between the actuator (a) and the rotation constraint (b) of the instrument. The reference torque is provided by a fine metal band (c) loaded with a brass washer (d) The fiber (e) is attached to a board strip f

The current to the PMMC was provided by a lab power supply, Agilent E3643A, which was manually controlled. The current was measured with a bench multimeter, Agilent 34450A, in the 100 $\mu \text {A}$ range. Ideally this instrument has a resolution of 1 nA. We observed a short term zero drift of the ampere meter of ${\pm }{2}\, \hbox {nA}$. With this current resolution, we obtained a torque resolution of 0.2 nN m.

Procedure

Torque Measurement The measurement of the torque applied on a fiber is a two-step process. In the first step, the pointer is deflected from its zero position to the defined angle $\varphi _0$ without a fiber mounted in the instrument. From the recorded current $I_0$, the restoring torque $T_{\mathrm {S}}$ of the taut bands of the PMMC is calculated. This measurement is only done once for each batch of samples. See Fig. 4i.

Fig. 4

Measurement of the torque applied to the fiber. First the restoring torque of the taut band $T_{\mathrm {S}}$ of the PMMC is determined (i), then the combined torque of the taut band and the fiber $T_{\mathrm {S}}+T_{\mathrm {F}}$ (ii). The torque generated by the moving coil (c) is determined by measuring the current through the coil with a precision ampere meter (a). The current is controlled by an adjustable power supply (b). The taut band of the PMMC not only acts as a support of the moving coil, but also as restoring spring (d)

For the second step the fiber is mounted in the instrument. The pointer is now again deflected to the defined angle $\varphi _0$, but this time the current required $I_1$ is larger than in the first step as the torque of the coil $T_1$ acts now against the restoring torque $T_{\mathrm {S}}$ of the taut bands and the torque of the fiber $T_{\mathrm {F}}$. The additional torque contributed by the fiber $T_{\mathrm {F}}$ is calculated as

$$\begin{aligned} T_{\mathrm {F}} = T_1 - T_0 = k_{\mathrm{T}} (I_1 - I_0) \end{aligned}$$

(1)

See Fig. 4ii. The instruments proportionality torque constant $k_{\mathrm{T}}$ is evaluated during calibration, see section 2.3. The currents $I_0$ and $I_1$ are found by manually adjusting the power supply until the pointer is exactly over the mark of the scale corresponding to $\varphi _0$. It takes about 10 s for the pointer to come to rest. The subtle effects of the viscoelasticity of the fibers are annihilated by the small movements required to manually adjust the pointer to its final position.

Measuring the Rate of Twist The angle of the twist was defined before the torque measurements. For the measurements presented in this paper, the maximum possible angle, i. e. the full deflection of the instrument, was used $\varphi _0 = 75^{\circ }$. From the twist torque curve published by Kolseth and Alf (1983), we know that this angle is still in the linear region of the deformation. The free length of the fiber between the glued joints was determined with an optical 3D measurement system, Alicona InfiniteFocus.

Reconstruction of the Fiber Geometry After the measurement, the metal hook was removed from the fiber and the remaining fiber together with the small board strip was embedded in resin. The embedded fibers were microtome cut such that there were at least five equidistant cross sections for each fiber taken (Wiltsche et al. 2011; Lorbach et al. 2012). Dependent on the free length, the distance between the microtome cuts was either 50 $\mu \text {m}$ for short fibers or 100 $\mu \text {m}$ for longer fibers. The microscopic images from the microtome were manually binarized. The microscopy images suffer from a very low contrast that prevents reliable automated edge detection. Figure 5 shows the microscopic images and the binarized cross sections of a TMP fiber and a kraft fiber side by side. From these binarized images, the torsion constant for the fiber was determined by numerically solving Eq. 10 for each fiber cross section image. Further details are outlined in Sect. "Determining the Torsion Constant of the Fiber".

Fig. 5

Cross sections of a partially collapsed TMP fiber with a small residual lumen (a) and a fully collapsed kraft fiber (b) The torsion constants derived from the binary images are $I_{\mathrm {T}} = {4190.73}\,{\mu \hbox {m}^{4}}$ and $I_{\mathrm {T}} = {2702.97}\,{\mu \hbox {m}^{4}}$ respectively. Microscopic images are contrast enhanced

Calibration

Preliminary Calibration The calibration makes use of the fact that the pointer of the PMMC is counter balanced. The PMMC was positioned with the axis of rotation in horizontal position. Small weights were placed on the pointer at a distinguished position. The weights were trimmed until the pointer was horizonal and at the end of the scale. A set of five weights was appropriately trimmed and weighed on a Sartorius BP 210 S lab balance. The average weight was ${\overline{W}} = {2.985} \,\text {mg}$. The distance from the axis to the distinguished position was measured with a sliding caliper as $d = {16.2} \,\text {mm}$. The maximum restoring torque of the taut bands of the instrument was $T_{\mathrm {max}} = {474.2} \,\text {nN m}$. Then, with the axis back in vertical position a current of $I_{\mathrm {max}} = {9.19} \,\mu \text {A}$ was required to deflect the pointer to the end of the scale. The torque constant of the PMMC was $k_{\mathrm{T}} = \frac{ T_{\mathrm {max}} }{ I_{\mathrm {max}} } = {51.55} \,\hbox {mN m A}^{-1}$.

Final Calibration The initial calibration was cross-checked by measuring the torque of torque standards, see Fig. 3i. For the standards, fine bands of platinum nickel PtNi10 alloy were used. These are available from the manufacturer Carl Haas Spiralfederfabrik with a specified torsional rigidity [25]. The bands used for validation had a torsional rigidity of $w_{\mathrm {T}} = {224.7}\,{\hbox {pNm}^2}$ and a rectangular cross section of $w = {55.0} \,\mu \text {m}$ by $h = {5.5} \,\mu \text {m}$. The torque of the standard was calculated from the specified torsional rigidity of the band and the dimensions by Eq. 2 (Samal 1955; Christoph March 1951; Hildebrand June 1957). With the rate of twist $\varphi ^{\prime } = \frac{\varphi }{l}$, the torque is

$$\begin{aligned} T_{\mathrm {R}} = w_{\mathrm {T}} \varphi ^{\prime } + \frac{W_{\mathrm {W}} (w^2+h^2)}{12} \varphi ^{\prime } + \frac{E w^5 h}{360} {\varphi ^{\prime }}^3 \end{aligned}$$

(2)

A M1 brass washer with a mass of $m_{\mathrm {W}} = {13.5} \,\text {mg}$ was used to align the band to the axis of rotation. $W_{\mathrm {W}}$ is the weight of the washer, E is the Young’s modulus of the band. The last two terms in Eq. 2, representing the effects of normal stresses (Weber 1921), account only for 0.5‰ of the torque and are negligible. The free length of the bands was measured with an optical 3D measurement system, alicona InfiniteFocus. The torque references were inspected for kinks in the band and spilled glue before measurement. All standards were measured only once, as many of the standards were damaged when removed from the instrument. Repeatability tests could therefore not be performed. 13 standards were successfully measured.

The calibration curve is seen in Fig. 6. The error $E_\mathrm {rms} = {5.15} \,\text {nN m}$ is mainly due to the slight misalignment of the axes and due to the small buckling of the band under torsional deformation. The instrument overestimated the torque by 11.8%. The torque constant of the PMMC was corrected accordingly to $k_T = {46.11} \,{\text {mN m A}}^{-1}$.

Fig. 6

Calibration of the instrument. 13 torque standards were measured after preliminary calibration. The instrument overestimated the torque of the standards by 11.8%

Validation

To demonstrate that the measurement procedure yields valid results, the data acquired from the 13 torque standards was used to obtain the shear modulus of the PtNi10 alloy from it. From the measured torque T, twisting angle $\varphi$, and the free length l, we obtain the torsional rigidity $w_{\mathrm {T}} = \frac{T l}{\varphi } = G I_{\mathrm {T}}$, which is the product of the shear modulus G and the torsion constant $I_{\mathrm {T}}$. To determine the torsion constant $I_{\mathrm {T}}$, we applied de Saint Venant’s torsion theory (Sokolnikoff 1956; Stephen 1970; Szabó 1960; Weber 1921). The exact solution for the torsion constant of a solid bar of rectangular cross section is

$$\begin{aligned} \begin{aligned} I_{\mathrm {T}}&= \frac{w h^3}{3} - \frac{64}{\pi ^5} h^4 \sum _{n=0}^{\infty } \frac{1}{(2n+1)^5} \tanh \left( \frac{(2n+1)\pi }{2} \frac{w}{h}\right) \\&\approx \frac{w h^3}{3} - \frac{64}{\pi ^5} h^4 \tanh \left( \frac{\pi }{2} \frac{w}{h} \right) \end{aligned} \end{aligned}$$

(3)

Only the first term of the series is required to calculate the torsion constant with an accuracy of better than 0.5%.

Sample preparation

Material Samples of two industrial pulps were subjected to the torsion experiments: softwood thermomechanical pulp (TMP) and softwood Kraft pulp. The Kraft pulp was an industrial, once dried, unbeaten, unbleached kraft pulp (mixture of spruce and pine, $\kappa$-number < 45). The TMP pulp is a once dried softwood thermomechanical pulp from industrial production. The cross sectional morphology of the fibers differed significantly depending on the pulping process. During the preparation, all of the kraft fibers collapsed, but some of the TMP fibers collapsed only partially with a residual lumen. Figure 5a depicts a partially collapsed fiber typical for TMP pulp. In total 37 fibers have been analyzed. The first set consisted of 20 fibers from TMP pulp, the second set was 17 fibers softwood Kraft pulp.

Preparation of the Fibers The preparation started with dried fibers from which a fiber suspension was formed by dilution with distilled water. A drop of the suspension was placed on a silicon pad and then covered by a second pad. This stack was placed between two carrier boards in the drying unit of a Rapid-Koethen sheet former and dried.

Fiber Selection From the dried fibers, suitable fibers were selected. To be selected, the fibers had to have a small straight section of about 500 $\mu \text {m}$. The selected fibers were stored in defined climate conditions, 50% relative humidity at 23$^{\circ }\hbox {C}$, until use. The fibers for sample preparation were chosen randomly from the pre selected fibers.

Mounting of the Fibers For the fibers to fit into the sample holder of the instrument, they were glued between a metal hook and a small piece of board with a grammage of 200 ${g/m^2}$ and a thickness of 280 $\mu \text {m}$. Figure 3i shows the arrangement. The fiber remained on the board during microtomy. A fast setting nail polish was used as glue. It was left to dry for at least 24 h to cure completely before testing.

Determining the torsion constant of the fiber

Pulp fibers consist of a primary wall P, and three secondary walls $S_1$, $S_2$, $S_3$. All layers are reinforced with microfibrils. In contrast to the other layers, the $S_2$ has a distinctive helical tilting, which is characterized by the micro fibril angle (MFA). Since the $S_2$ layer takes up the biggest volume fraction, pulp fibers are commonly modeled by taking only the structure of the $S_2$ layer into account. As in the $S_2$ layer the microfibrils are oriented roughly in the direction of the fiber axis, i. e. the MFA is small, the fiber is modeled as a transverse isotropic material with the plane of isotropy perpendicular to the longitudinal fiber axis (Seidlhofer et al. Aug 2019). The material model is incompressible, which is a simplification, as very recent work is suggesting a compressible plasticity model to account for the fiber wall nanoporosity (Seidlhofer et al. 2021).

The fiber is twisted around the longitudinal axis. Hence, the longitudinal shear modulus $G_{\mathrm {L}}$ is the relevant material parameter. In shear tests, stress $\tau$ and the shearing of the edges $\gamma$ are perpendicular ($\tau = G_{\mathrm {L}} \gamma$) to each other. This orientation is indicated in Fig. 1. We assume that warping torsion of the irregular fiber cross section is of negligible magnitude (Parkus 1966) and apply the torsion theory of de Saint Venant.

The de Saint Venant torsion angle of twist $\varphi$ for a beam with uniform cross section is

$$\begin{aligned} \varphi = \frac{T l}{G_{\mathrm {L}} I_{\mathrm {T}}} \end{aligned}$$

(4)

where T is the torque and $I_{\mathrm {T}}$ the torsion constant. The torsion constant $I_{\mathrm {T}}$ is a cross-sectional geometrical parameter. The cross section of a natural fiber varies considerably over the length of the fiber. In a pilot survey, we microtomized two fibers, one from each of the two pulps, respectively. For each fiber at least 90 cross sections, 20 $\mu \text {m}$ apart, were acquired and the torsion constants determined. The variation of the torsion constant along the fiber axis was large for both fibers, the min-max ratio was at least $1\mathop {:}10$. For the TMP fiber the distribution of the values was nearly uniform, thus values close to the extremes occurred quite frequently. To avoid the effect of slicing the fiber sample at an unsuitable position, where the torsion constant is extreme, we developed a simple model for the deformation of the fiber under torsion based on several cross sections, the apparent torsion constant. We model the fiber as a series of segments with uniform cross sections as shown in Fig. 7. It is assumed that each cross section center is lying on the torsional axis. Finally, we approximate the apparent torsion constant $I_{\mathrm {T}}$ of the fiber by the discrete torsion constants $I_{\mathrm {T}}^i$ of the segments.

Fig. 7

To compute the apparent torsion constant $I_{\mathrm {T}}$ of the fiber, it is partitioned into n segments. Segment i is described by its torsion constant $I_{\mathrm {T}}^i$, its length $l_i$ and its twisting angle $\varphi _i$

The torque T is the same for all segments and the fiber is of an homogeneous material. We apply de Saint Venant torsion to all segments

$$\begin{aligned} \varphi _i = \frac{T l_i}{G_{\mathrm {L}} I_{\mathrm {T}}^i} \end{aligned}$$

(5)

and take into account that the twisting angles of the segments $\varphi _i$ accumulate along the fiber

$$\begin{aligned} \varphi = \sum _{i=1}^{n} \varphi _i. \end{aligned}$$

(6)

With Eq. 5 and 6 the shear modulus can be computed from the length increments $l_i$ and the torsion constants $I_{\mathrm {T}}^i$ of the fiber segments as

$$\begin{aligned} G_{\mathrm {L}} = \frac{T}{\varphi } \sum _{i=1}^{n} \frac{l_i}{I_{\mathrm {T}}^i}. \end{aligned}$$

(7)

The apparent torsion constant $I_{\mathrm {T}}$, that describes the deformation of the fiber as a beam with uniform cross section, is defined as

$$\begin{aligned} I_{\mathrm {T}} = \frac{l}{ \sum _{i=1}^{n} \frac{l_i}{I_{\mathrm {T}}^i}}. \end{aligned}$$

(8)

The torsion constant $I_{\mathrm {T}}^i$ for each of the n segment cross sections $A_i$ was calculated from the respective cross section image acquired with microtomy, compare Fig. 5. We are first introducing the Prandtl stress function $\psi$. Then we solve the Poisson’s equation stated in Eq. 9, cf. (Sokolnikoff 1956, Eq. 35.7), for the given boundary value problem with an in-house FEA code.

$$\begin{aligned} \frac{\partial ^2 \psi }{\partial y^2} + \frac{\partial ^2 \psi }{\partial z^2} = -2 \text{ } \text{with} \text{ } \psi = c_j \, \text {on} \, \partial \Omega _j \, \text {for} \, j \, = \, 1,\dotsc ,m \end{aligned}$$

(9)

When the fiber shows a lumen, i. e. the cross section has holes, the cross section is defined by m boundary curves. The stress function $\psi$ can assume different but constant values $c_j$ on each boundary curve $\partial \Omega _j$. The Dirichlet boundary values $c_j$ are calculated with the technique given in Stephen (1970).

Then, with the solution of the stress function $\psi$, the torsion constant is computed by evaluating the integral in Eq. 10, cf. (Sokolnikoff 1956, Eq. 35.9) and (Gruttmann et al. 1999, Eq. 20), respectively.

$$\begin{aligned} I_{\mathrm {T}}^i = -\int _{A_i} \left( \frac{\partial \psi }{\partial z} z + \frac{\partial \psi }{\partial y} y \right) dA_i. \end{aligned}$$

(10)

Results

Validation To validate the instrument and the procedure the shear modulus of the bands used as torque standards was determined. The torsion constant for the rectangular cross section is $I_{\mathrm {T}} = {2858.8}\,{\mu \hbox {m}^4}$. The shear modulus of the band material, PtNi10, is given by the manufacturer as $G_{\mathrm {PtNi}} = {73.06} \, {\mathrm{ GPa}} \pm 5\%$ [25]. The measured shear modulus is $G_{\mathrm {M}} = (77.99 \pm 7.09) \,\mathrm{GPa}$. The measured value deviates 6.75% from the shear modulus given in the material data sheet. The measurement method has hence been validated successfully.

Shear modulus of wood pulp fibers The average values of the measured quantities for length l, torque T, and torsion constant $I_{\mathrm {T}}$ and the resulting shear modulus G of the fibers are summarized in Table 1, error margins are 95% confidence limits. Two TMP outliers with very high shear moduli were removed from the data set. Closer inspection of the microscopy images showed that these samples were actually a bundle of not fully disintegrated fibers. All other samples were individual fibers. The distribution of the shear modulus is right skewed. The asymmetry of the distribution demonstrated by the box plot in Fig. 8.

Table 1 Summary of the measurements on fibers. The error margins are 95% confidence limits

Fig. 8

Shear modulus for TMP and kraft fibers. The distribution for kraft fibers is noticeably right skewed. Two outliers due to deficient fiber morphology were removed from the data set

Discussion and conclusions

We designed a fiber torsion tester based on a moving coil taut band instrument. For analysis of the fibers we assumed a transverse isotropic material for the fiber, where the preferred direction is aligned to the torsional axis and warping is not hindered. The torsional constant $I_{\mathrm {T}}$ of the tested fibers was calculated from the actual fiber cross section which has been photographed under a microscope. The fiber cross sections are assumed to be aligned with the torsion axis, de Saint Venant’s theory of torsion is applied to calculate an apparent torsion constant $I_{\mathrm {T}}$ of each fiber. We validated our instrument by measuring the shear modulus of a linear elastic platinum wire with well defined torsional properties.

The fiber wall shear moduli for Kraft and TMP fibers are summarized in the box plot, Fig. 9. The material of the TMP fibers, with a longitudinal shear modulus of $G = {2.13}\, {\text {GPa}}$, turned out to be weaker than the kraft fibers, with a shear modulus of $G = {2.51} \,{\text {GPa}}$. A similar behavior has already been observed for the fiber E-modulus in longitudinal direction where TMP fibers were weaker than Kraft pulp fibers (Neagu et al. 2006). It has been reasoned that the harsh production process of the TMP fibers is damaging the fibers more than the removal of the lignin in the Kraft cooking process (Neagu et al. 2006). Also nanoscale FEM models for pulp fibers reveal a higher longitudinal stiffness for Kraft fibers compared to TMP fibers (Borodulina et al. 2015). The considerably lower stiffness of lignin compared to crystalline cellulose leads in these models to a higher E-modulus for the Kraft fibers because much of the lignin is removed from the fiber wall in the cooking process.

When we focus on the torsional rigidity of the individual fibers we, however, find that the TMP fibers are stronger than the Kraft fibers. We obtain a torsional rigidity of $w_{\mathrm {T}} = (7.81 \pm 2.06)\,{\hbox {pNm}^2}$ for TMP fibers and $w_{\mathrm {T}} = (5.63 \pm 4.44) \, {\hbox {pNm}^2}$ for kraft fibers. This difference is due to the larger cross sections, and the less collapsed state of the TMP fibers which leads to an increase in the torsion constant $I_{\mathrm {T}}$. The cross sectional shape of the TMP fibers thus overcompensating the smaller shear stiffness of the material.

Fig. 9

Torsional rigidity $w_{\mathrm {T}}$ for TMP and kraft fibers. The distribution for kraft fibers is noticeably right skewed

The variation of the shear modulus was smaller than we expected for a biological material and a mix of fibers from different wood species. This supports the idea that the shear modulus of wood pulp fibers is indeed a material property. In Fig. 10 we see that the apparent torsion constant varies considerably. However, assuming that the shear modulus G is a material constant, the torsional rigidity also should show more variability.

The design of an instrument with less variation is desirable, but the constructive effort for better alignment of the sample, which we see as main contributor to the variation, is high and would make the instrument rather difficult to use.

Fig. 10

Torsion constant $I_{\mathrm {T}}$ for TMP and kraft fibers. The values for the torsion constant vary more than an order of magnitude

Future Work To complete the characterisation of the wood pulp fibers, the static shear modulus must be complemented with viscoelastic properties. The setup described in this work could be upgraded with a Laser displacement sensor for a dynamic measurement of the fiber twisting angle and a suitable force control system to perform creep- and relaxation tests.

Supplement: error analysis of the homogeneous mechanical model

To validate the calculation of the apparent torsion constant from a simplified fiber geometry we compared it to the simulation of a more realistic fiber geometry that takes the fibrilar structure of the fiber into account. A cross section of one of the TMP fibers was used as base of a uniform prismatic beam. For this cross section a torsion constant $I_{\mathrm {T}} = {11575.05}\,{\mu \hbox {m}^4}$ was calculated with the numerical method described in Sect. "Determining the Torsion Constant of the Fiber". For the application of de Saint Venant’s theory to the beam a longitudinal shear modulus of $G = {2.5}\, {\text {GPa}}$, a length of $l = {1000} \,\mu \text {m}$, and an angle of twist of $\varphi = {9}{^{\circ }}$, was assumed. The prediction for the torque $M_{\mathrm {T}}$ required to deform the fiber is

$$\begin{aligned} M_{\mathrm {T}} = G I_{\mathrm {T}} \frac{\varphi }{l} = {4.545}\,\text {nN m} \end{aligned}$$

(11)

The simulation of the same geometry yields a torque of $M_{\mathrm {S}} = {4.789} \,\text {nN m}$. Considering the simulation as the ground truth the relative error is small, $E_{\mathrm {R}} = -5.095 \,\%$, and to some extent caused by the boundary conditions of the FEA simulation, as the error decreases with the fiber length.

In a refined model, anisotropy was introduced to account for microfibril reinforcement and the dependency of the torque on the microfibril angle was established. For this simulation a transverse isotropic material was assumed. The parameters were $E_{\mathrm {L}} = {10.0}\,{\text {GPa}}$, $E_{\mathrm {T}}={3.0}\, {\text {GPa}}$, $G_{\mathrm {T}} = {1.0} \,{\text {GPa}}$, $G_{\mathrm {L}} = {2.5}\, {\text {GPa}}$, and $\nu _{\mathrm {LT}} = 0.23$. The simulation showed that the torque required to twist the fiber decreases with increasing MFA.

Fig. 11

Dependence of the normalized torque on the microfibril angle. The torque on the fiber is related to the a perfectly aligned fiber, i. e. $\mathrm {MFA} = 0^{\circ}$. The range of MFAs found in the $S_2$ layer of wood pulp fibers is highlighted

For Fig. 11 we relate the torque of a fiber modeled with a non-zero MFA to the torque on a perfectly aligned fiber. The estimation error of the torque, as well as the shear modulus, induced by non-zero MFA, is within 5% if the microfibril angle MFA is below 14.5${^{\circ }}$. Since the MFA of the $S_2$ layer is often in the range ${0}{^{\circ }}\ \hbox {to}\ {10}{^{\circ }}$ (Salmén 2018; Courchene et al. 2006) the error is less than 2.5% and therefore neglectable compared to other error implications. Furthermore, we note that assuming linear elasticity, the torque is equivalent for both rotation directions, be it with or against the MFA direction. The reason is that we assume equivalent stiffness of the fibrils for elongation and compression, hence the microfibrils are bearing the same load in both rotation directions. Additionally, an initial twist has no influence in linear elastic analysis. As these effects might be relevant for large twist angles, we select less twisted and straight fibers and keep the twist angle small in the measurements. Therefore, we consider these effects to be negligible.

We conclude that the errors induced by assuming a homogenous material and applying the analytical de Saint Venant torsion theory with a numerical computed torsion constant are within acceptable bounds.