Introduction

Natural fibers, i.e., fibers consisting mainly of cellulose, hemi-cellulose and lignin, can be found in many biomaterials like flax, wood, jute and paper (Berglund 2012; Sood and Dwivedi 2018). Because of their high specific strength, biodegradability, low-cost production, recycle-ability, vast availability and easy processing, these natural fibers are becoming a more important constituent in multiple engineering materials, such as wood-cement composites (Caprai et al. 2019), carbon fiber-cellulose composite paper (Yunzhou and Biao 2014), woven flax fiber composites (Chegdani and El Mansori 2018) and natural fiber fabrics (Francucci et al. 2010). Natural fibers offer opportunities for sustainable clean composites, however, not without potential problems. For instance, the geometrically imperfect fiber walls can deteriorate the composite performance, or more importantly, properties of natural fiber composites degrade when exposed to moisture or water. In general, because of their hydrophilic nature, an imposed change in moisture content due to a change in relative humidity, wetting, printing, etc. results in swelling of the natural fibers, which greatly affects the geometric and mechanical properties (Uesaka et al. 1992; Johnson et al. 2017; Jajcinovic et al. 2018; Hashimoto et al. 2003; Chen et al. 2019; Bosco et al. 2015). Also for synthetic fibers, loss of dimensional stability related to hygroscopic changes are of key importance (Agrawal et al. 2013; Guo et al. 2016; Nunna et al. 2012). As a result aging of fiber-based materials, such as paper products, are strongly effected by moisture content, which controls the life expectancy (Zou et al. 1996a, b). Therefore, full understanding of the hygroscopic behavior of a single fiber is needed to predict macroscopic dimensional changes and to unravel the microscopic deformation and failure mechanisms such as fiber matrix debonding in composites and fiber–fiber debonding in paper sheets. This work proposes a novel method for a precise in-situ measurement of the full-field hygroscopic strain of individual fibers in response to moisture uptake.

Before discussing the hygro-expansion quantification techniques proposed in the literature, first some general properties of natural fibers are briefly discussed. Natural fibers used in paper products are typically long, with a hollow ribbon-like shape, consisting of multiple layers that are usually named, starting from the surface, S1, S2 and S3. Each layer consists of smaller micro-fibrils of mostly crystalline cellulose chains, interrupted by amorphous parts, that are aligned in a helical shape along the fiber axis (Neagu et al. 2006; Hubbe 2014). The angle of these micro-fibrils (MFA) strongly affects their mechanical properties (Page et al. 1972; El-Hosseiny and Page 1975; Mark and Gillis 1983; Reiterer et al. 1999) and the magnitude and principal directions of the hygro-expansion (Yamamoto et al. 2001; Meylan 1972). Natural fibers are optically semi-transparent with a refractive index of roughly 1.6, which increases with the moisture content (Fabritius and Myllylä 2006). Page and Tydeman (1962) have stated that a single natural fiber shrinks roughly 20–30% in transverse and 1% in longitudinal direction, upon drying from an over-saturated wet fiber to a completely dry state.

Already in 1965, Tydeman et al. (1965) investigated the dimensional changes of single fibers using micro-radiography combined with a vacuum chamber, where the outer dimension of a fiber web was projected on an X-ray sensitive film before and after drying, allowing them to obtain a change in fiber width with a strain precision of maximum 1 × 10−2Footnote 1, while longitudinal measurements were not possible. Meylan (1972) investigated the influence of the MFA on the longitudinal shrinking behavior of natural fibers by using an universal S.I.P trioptic microscope combined with a climate chamber. Salt solutions, which are limited to a few discrete values of relative humidity, were used to change the relative humidity, while the microscope imaged the dimensional change of the fiber. However, these tests were time consuming, since the relative humidity was decreased in eight discrete steps, which took two days each to reach an equilibrium. Additionally, due to the apparatus’ low measurement resolution (±1.25 \(\mu\)m), only longitudinal shrinkage measurements were possible on fibers longer then 4 mm, with a strain precision of 3 × 10−4Footnote 2. Nanko and Wu (1995) investigated the longitudinal shrinkage of fibers using reflection-type scanning laser microscopy, where they applied a silver powder on the fiber surface for tracking, while simultaneously obtaining surface height profiles (topographies). Combining these topographies allowed them to obtain the shrinkage in longitudinal direction before and after a drying step. The transverse shrinkage was not measured, moreover, no strain data was provided. Lee et al. (2010) used Atomic Force Microscopy (AFM) in tapping mode to determine the longitudinal and cross-section dimensional changes (of cellulose fibrils instead of fibers) using salt solutions to keep the relative humidity constant and bring the fibrils to equilibrium, after which the relative humidity was increased or decreased to 50% while consecutive AFM scans were captured. This allowed to obtain the dimensional change due to moisture uptake or release with, respectively, a longitudinal and transverse strain precision of 1 × 10−2Footnote 3, however with a limited field of view. Table 1 contains a brief description of the above-mentioned methods and the reported precision. The method proposed here is added to reveal its potential.

Table 1 Single fiber hygro-expansion techniques proposed in the literature with, if available, a calculated precision
Full size table

This paper demonstrates a novel, more precise, easy-to-apply method to directly quantify the full-field continuous dimensional changes of natural fibers during wetting and drying, with a longitudinal and transverse strain precision of, respectively, 1 × 10−4 and 7 × 10−4, as listed in Table 1.

Within the proposed method, the fiber hygro-expansion is measured by correlating fiber topographies obtained with a profilometer using Global Digital Height Correlation (GDHC) (Neggers et al. 2012). This allows direct precise full-field measurements of the three dimensional displacement and surface strain fields of the fiber exposed to a continuously changing relative humidity inducing moisture uptake or release, thereby extending the work of Lee et al. (2010). Furthermore, no extensive sample preparation is required and the experiments are less time consuming than most previously reported methods. The method is applicable to different fiber types, materials and geometries as given in Johnson et al. (2017), Jajcinovic et al. (2018), Hashimoto et al. (2003), Chen et al. (2019), making the method viable for a vast range of applications.

Experimental methodology

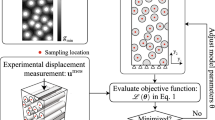
A schematic representation of the experimental methodology is shown in Fig. 1. To keep the fiber within the field of view (FOV) of the microscope while constraining it minimally, a dedicated clamping method, which uses two highly compliant (10 mm long, 50 \(\mu\)m diameter) nylon threads that are fixated at both ends with a droplet of glue, was developed and optimized. The two nylon threads minimally fixate the fiber at two spots, providing complete freedom for hygro-expansion of the fiber while only reducing the fiber’s rigid body motion and twisting, see Fig. 1a. The fiber’s region of interest (ROI) is in the center between the two threads. The fiber is subsequently sprayed with Polymethylmethacrylate micro-particles immersed in ethanol using an airbrush, resulting in a pattern on the fiber’s surface. The micro-particles are a essential element needed for tracking with the GDHC algorithm (Kammers and Daly 2011; Dong and Pan 2017), as explained below.

Different types of profilometers were compared to obtain high quality topographies of the fiber’s top surface and not the internal structure or bottom surface. It was found that vertical scanning interferometry (VSI) optical microscopy is preferred over AFM since it is non-contact and has a small acquisition time with a relatively large FOV. Additionally, VSI was found to yield better results than confocal optical microscopy, which is an intensity based profilometry technique. Fibers become more transparent during testing, to which confocal profilometry was found to be more sensitive. For this work a 100 \(\times\) objective in combination with a FOV multiplier lens up to 2 \(\times\) was chosen for the VSI profilometer (Bruker NPFlex), allowing a magnification up to 200 \(\times\), and a minimal FOV of \(30 \times 40 \, \mu \hbox {m}^2\), corresponding to a pixel size of 29 nm for the \(1376 \times 1040\) pixel surface topography. Green light is used for increased lateral resolution over white light, and consequently increasing the resulting strain resolution obtained from GDHC.

The prepared fiber is placed in a climate chamber underneath the optical profiler, shown in Fig. 1b. A flexible rubber tube, shown in green, is clamped around the objective to close down the control volume as well as possible. An external controller regulates the temperature and relative humidity inside the climate chamber, by controlling a pre-mixed flow of dry nitrogen and humid air into the climate chamber. Before testing, the fiber is first equilibrated by maintaining the starting relative humidity and temperature constant for two hours. During testing, the relative humidity is increased while the optical microscope takes consecutive surface topographies, during which the relative humidity and temperature are logged. Note that the moisture content shows a bi-modal response to a step in relative humidity, i.e. the first \(\sim\)90% of the step in moisture content occurs within a minute, however, the remaining response to full saturation occurs over a time frame of hours (Jajcinovic et al. 2018). Therefore, one should be very careful when converting the measurement of the hygro-expansion as a function RH into hygro-expansion as a function moisture content. All experiments are conducted at a constant temperature of 23 \(^\circ\)C.

After testing, the fiber topographies are processed by the GDHC algorithm (see Sect. “Global Digital Height Correlation Algorithm”), developed previously to obtain full-field deformation data for different micro-mechanical applications (Han et al. 2010; Van Beeck et al. 2013; Shafqat et al. 2018). The optimization of the GDHC algorithm for the current problem is elaborated in Sect. “Global Digital Height Correlation Algorithm”. The algorithm provides the three-dimensional displacement vector of each point on the surface, which allows to compute the surface deformation, giving insight in the fiber kinematics. The surface strains along the longitudinal (\(\epsilon _{ll}\)) and transverse (\(\epsilon _{tt}\)) directions are determined as proposed in Shafqat et al. (2018). Subsequently, to achieve optimal precision in the fiber strains, the mean strains are computed from the strain field, resulting in the mean longitudinal and transverse surface strains as a function of relative humidity. Note that the full strain field is accessible as well, e.g., for analysis of inhomogeneous fiber swelling.

Fig. 1
figure 1

Schematic representation of the experimental procedure with: a the dedicated clamping method (by means of two nylon threads) of a single fiber which is sprayed with micro-particles, b climate chamber placed underneath an optical profiler, allowing in-situ single fiber testing and c topographies obtained from the optical profiler are processed using Global Digital Height Correlation to obtain the average longitudinal and transverse surface strains of a single fiber

Full size image

Global Digital Height Correlation algorithm

Digital Image Correlation (DIC) in its 2D form is an image matching algorithm that allows full-field displacement measurements, which exists in a “local” (subset) or a “global” (whole FOV) form (Bruck et al. 1989; Neggers et al. 2016; Hild and Roux 2012). Global DIC is chosen over local DIC since it is more robust against lost data and pattern degradation (Bergers et al. 2013), which is known to occur when testing natural fibers, while it has been demonstrated that global DIC can more readily be fine tuned towards a specific application (Neggers et al. 2012; Kleinendorst et al. 2016; Kleinendorst, submitted for publication). Here, however, height profiles are used instead of gray-scale images. Therefore, a Global Digital Height Correlation (GDHC) approach dedicated to fiber swelling is adopted based on topography conservation, i.e. the height value at a certain pixel position \(\vec {x}\) in the reference topography f is equal the height value at the new position (\(\vec {x} + \vec {u}(\vec {x})\)) in the deformed topography g minus the out-of-plane displacement (Neggers et al. 2014), which reads:

$$\begin{aligned} \psi (\vec {x}) = f(\vec {x}) - (g(\vec {x} + u(\vec {x})\vec {e}_x + v(\vec {x})\vec {e}_y) - w(\vec {x})), \end{aligned}$$
(1)

in which u and v are the in-plane components of the displacement in, respectively, x-direction (\(\vec {e}_x\)) and y-direction (\(\vec {e}_y\)) and w denotes the out-of-plane displacement in z-direction (\(\vec {e}_z\)) while \(\psi\), the residual, represents acquisition noise and height distortions not captured by w. Note that both f and g contain height information as a function of the two-dimensional image coordinate, hence the 3D displacement vector (\(u(\vec {x}) = u(\vec {x})\vec {e_x}+v(\vec {x})\vec {e_y}+w(\vec {x})\vec {e_z}\)) is a function of the 2D position vector (\(\vec {x} = x\vec {e_x}+y\vec {e_y}\)). The residual, \(\psi\), is minimized, i.e.:

$$\begin{aligned} \mathop {{{\,\mathrm{\mathrm{arg\,min}}\,}}}\limits _{\vec {u}(\vec {x})}(\Phi ) = \mathop {{{\,\mathrm{\mathrm{arg\,min}}\,}}}\limits _{\vec {u}(\vec {x})} \Big ( \int _{\Omega }^{}\psi ^2d\vec {x}) \Big ), \end{aligned}$$
(2)

in which \(\Omega\)The solution to this non-linear minimization is the global FOV. To this end, an approximated displacement field, \(\vec {u}^*(\vec {x},\underline{\lambda })\), is introduced, spanned by shape functions, \(\vec {\phi }(\vec {x})\), associated with degrees of freedom (DOF), \(\underline{\lambda }\);

$$\begin{aligned}& \vec{u}^*(\vec{x},\underline{\lambda}) = u^*(\vec{x},\underline{\lambda})\vec {e}_x + v^*(\vec{x},\underline{\lambda}) \vec{e}_y+w^*(\vec{x},\underline{\lambda})\vec {e}_z \quad \text {with} \,\, \underline{\lambda} = \{\underline{\lambda}^x, \underline{\lambda}^y, \underline{\lambda}^z\}, \end{aligned}$$
(3)
$$\begin{aligned}&\vec {u}^*(\vec {x},\underline{\lambda }) = \sum _{i=1}^{n}\lambda _i^{x}\phi_i^{x}(\vec {x})\vec {e}_{x} + \sum _{j=1}^{n}\lambda _j^{y}\phi _j^{y}(\vec {x})\vec {e}_{y}+ \sum _{k=1}^{n}\lambda _k^{z}\phi _k^{z}(\vec {x})\vec {e}_{z}. \end{aligned}$$
(4)

The goal is to minimize \(\Phi\) with the 3n shape functions with DOF \(\underline{\lambda }\) where \(\phi_i\) is a series of basis functions that should be rich enough to capture the fiber swelling kinematics and \(\underline{\lambda }\) are to be determined, which can be written as:

$$\begin{aligned} \mathop {\mathrm{arg\,min}}\limits _{\underline{\lambda }}(\Phi (\underline{\lambda })). \end{aligned}$$
(5)

The solution to this non-linear minimization problem can be found by using an iterative modified Newton–Raphson scheme which has been derived in a consistent manner (Neggers et al. 2016). As shown in Neggers et al. (2016), when four assumptions (linearly independent basis functions, small residual, small rotations and good initial guess) hold, as is the case for fiber swelling as shown below, the true image gradient can be reduced to an image gradient that only depends on the reference image, so it only has to be computed once. Moreover, it was demonstrated in Neggers et al. (2016) that the strain accuracy does not depend on the chosen image gradient, if convergence is found, as will be demonstrated below. Here, however, the corresponding topography gradient (instead of the image gradient) is required by the optimization scheme:

$$\begin{aligned} \vec {G} = \frac{\partial f}{\partial x}\vec {e}_x + \frac{\partial f}{\partial y}\vec {e}_y - \vec {e}_z. \end{aligned}$$
(6)

More details of the derivation of the above given GDHC algorithm can be found in Neggers et al. (2016, 2014).

The type of basis function required to capture the minimal kinematically admissible 3D surface displacement field that fully describes the fiber swelling kinematics can be determined before testing. This optimal kinematic regularization must contain the following three displacement, three rotation and six deformation (expansion and bending) modes:

  • rigid body translation in the three principal directions (each described with a 0th-order polynomial),

  • homogeneous hygroscopic expansion along three principal directions (1st-order polynomial),

  • rotation, with magnitude \(\alpha\), around the three principal directions (1st-order polynomial):

    • in-plane rotation (around the z-axis):

      $$\begin{aligned} \vec{u} = (x (\text{cos} (\alpha_z)-1)-y \text{sin} (\alpha_z))\vec{e_x} + (x\text{sin}(\alpha _z)+y(\text{cos}(\alpha_z)-1)) \vec {e_y}, \end{aligned}$$

    • out-of-plane rotation (around the y-axis):

      $$\begin{aligned} \vec{u} = (x (\text{cos}(\alpha_y)-1)-z \text{sin}(\alpha_y)) \vec{e_x} + (x \text{sin}(\alpha_y)+ z(\text{cos}(\alpha_y)-1))\vec{e_z}, \end{aligned}$$

    • fiber axis rotation (around the x-axis):

      $$\begin{aligned} \vec {u} = (y(\text {cos}(\alpha _x)-1)-z\text {sin}(\alpha _x))\vec {e_y} + (y\text {sin}(\alpha _x)+z(\text {cos}(\alpha _x)-1))\vec {e_z}, \end{aligned}$$

  • small-strain approximation of bending, with magnitude \(\kappa\), in three directions (2nd-order polynomial):

    • in-plane bending (around the z-axis): \(\vec {u} = \kappa_zx^{2}\vec{e_y} + O(x^{4})\),

    • out-of-plane bending (around the y-axis): \(\vec{u} = \kappa_yx^{2} \vec{e_z} + O(x^{4})\),

    • fiber axis bending (around the x-axis): \(\vec{u} = \kappa_xy^{2} \vec{e_z} + O(y^{4})\),

with x, y and z the three global axes. Note that the formulation for bending stems from a Taylor expansion around the center of the fiber positioned at the origin of the global axes. In case of fiber swelling, the bending magnitude will be small, therefore a second-order polynomial basis function is sufficient to properly describe the fiber swelling kinematics, which is verified in Fig. 4 below by analyzing the effect of the polynomial’s order on the mean residual value, similar to the analysis done by Neggers et al. (2014).

Equation 6 shows that the surface gradient drive the correlation, which implies that the applied pattern must reveal adequate gradients in order to properly determine the displacement field. It is for this reason that the fiber is decorated with micro-particles. The edges of the particles are hard to measure using optical height microscopy, as the steep angle at the edge of a particle results in data loss, which consequently results in higher residual values in these regions. A masking algorithm is applied to counteract this phenomenon. A paper fiber is tested for a relative humidity change from 50 to 80%, of which the reference topography is shown in Fig. 2a. A zoomed in view is provided in which two 500 nm particles with black regions around their edges are indicated. These black regions indicate lost data points in the topography [not a number (NaN)], originating from the sharp edges of the particles. Figure 2b shows the residual field between the first and the last topography of the experiment, correlated using a second-order polynomial. A dilatation algorithm is used to mask the pixels inducing NaNs in the reference topography, which masks out the higher residual values. A dilatation of 0 refers to the initial topography, whereas a dilatation of n refers to masking a band of n pixels wide around a NaN pixel, shown in Fig. 2b–d. It can be seen that with increasing dilatation, more of the higher residual pixels are masked. However, dilating too many pixels results in a reduced pattern quality, as can be seen in Fig. 2d, in which the two 500 nm particles indicated in the reference image are completely masked out. Hence, in the following experiments, a dilatation of 2 is used in all correlations.

Fig. 2
figure 2

A paper fiber is tested from a relative humidity of 50–80%, to show the potential of the pixel masking algorithm with: a reference topography, a zoomed in view is provided which shows the lost data, i.e. around two 500 nm particles and b–d three residual fields between the first and the last topography, with, respectively, a dilatation of 0 (initial topography), 2 and 4 rows around a NaN pixel. A dilatation of 2 is chosen, which masks out almost all of the higher residual regions, but does not completely mask out the two 500 nm particles indicated by the red circles in the reference image. This does happen for a dilatation of 4, resulting in a deteriorating pattern

Full size image

Types of fibers considered

Four fiber types are tested, of which scanning electron microscopy (SEM) images are shown in Fig. 3, respectively (a) rectangular viscose, (b) trilobal viscose, (c) 3D-printed hydrogel and (d) eucalyptus paper. Each fiber has a different cross-section, surface topography and hygroscopic behavior. A schematic drawing of the cross-section is added, which is used later to indicate the type of fiber. Rectangular viscose, shown in Fig. 3a, has a width and thickness of respectively \(50 \times 3\, \mu \hbox {m}\) and almost no surface roughness. Note that viscose is an artificially created fiber consisting of cellulose chains oriented in longitudinal direction (Chen 2015). Trilobal viscose, shown in Fig. 3b, has a diameter of \(35\,\mu \hbox {m}\) and some surface roughness lines along the longitudinal direction. 3D-printed hydrogel (Putti et al. 2019), shown in Fig. 3c, has a circular shape with a diameter of \(50\, \mu \hbox {m}\) and some minor surface roughness is visible. Due to its intrinsic ability for large moisture uptake, large hygroscopic dimensional changes are expected for this fiber. Finally, eucalyptus paper fibers, shown in Fig. 3d, have a diameter of \(35\, \mu \hbox {m}\) and a rough surface due to their fibrilic layered structure. The white calcium-carbonate particles are present since this fiber (Eucalyptus Globulus) is carefully extracted, by means of, delaminating an original sheet of paper and pulling out the naturally sticking out fibers without touching or mechanically loading the ROI.

Fig. 3
figure 3

SEM images of the tested fibers: a rectangular viscose, b trilobal viscose, c 3D-printed hydrogel and d eucalyptus paper. The schematic drawings represent the cross-section of each fiber, used later to indicate the type of fiber

Full size image

Results and discussion

Qualitative assessment and optimization of the GDHC method

The method’s potential is illustrated by measuring the hygro-expansion of the above mentioned fibers, starting with rectangular viscose. Three of these fibers have been prepared, each with a different pattern density of \(1\, \mu \hbox {m}\) particles, shown in Fig. 4a–c. Zoomed in views of the three fibers reveal that particle clustering occurs, which appeared to be unavoidable. This clustering is detrimental for the pattern as it accumulates data loss around the edges of or in between the particles. The fibers are tested with an objective of \(100\,\times\), reducing the FOV to \(60 \times 80 \,\mu \hbox {m}\)2, a vertical scanning range of \(20 \,\mu \hbox {m}\), resulting in a single topography scanning time of 9 s. Fiber swelling should occur homogeneously over the fiber surface, which suggests that a first-order polynomial should be sufficient to describe the kinematics. However, as already discussed, non-linear kinematics can arise due to, e.g., bending of the fiber due to inhomogeneous contact conditions. Therefore, higher-order polynomials are used to describe the global displacement field.

The three fibers are tested for a relative humidity increasing from 50 to 88%, and the mean residual using, respectively, polynomials of order 1–5 are shown in Fig. 4d–f. Figure 4f directly shows that severe particle clustering leads to an increase in the mean residual by approximately a factor of two, irrespective of the polynomial’s order. Additionally, Fig. 4d–f confirm the expected incompleteness of the first-order polynomial, whereas the mean residual tends to converge after an order of two. Important to note here is that the mean residual keeps decreasing even after using a fifth-order polynomial, which happens since higher-order polynomials also tend to capture image noise. However, the additional decrease in mean residual after the second-order polynomial is insignificant. Hence, second-order polynomials are used in the subsequent experiments.

The mean surface strain in the longitudinal and transverse directions versus relative humidity of the three fibers is shown in Fig. 4g–i. All fibers are subjected to two wetting cycles, both with a relative humidity increasing from 50 to 88%, where the strains start at zero for the second wetting cycle. The three fibers show a comparable difference in response between the first and second cycle although the fiber-to-fiber difference is quite substantial, as was also observed in Meylan (1972), Tydeman et al. (1965), Lee et al. (2010). A negative strain in longitudinal direction for the first wetting cycle could imply a positive dried-in strain, imposed during manufacturing, which is released during the first wetting cycle (Chen 2015). Furthermore, a dense pattern results in higher mean residual values, due to visible pattern degradation during the experiment, which consequently results in a decreased precision of the strain compared to the other two patterns. This implies that severe particle clustering deteriorates the quality of the correlation. Additionally, the pattern density shown in Fig. 4a, b is rather sparse compared to typical high-quality DIC patterns (Dong and Pan 2017; Hoefnagels et al. 2019). Nevertheless, since the algorithm uses a global approach in combination with a second-order polynomial, these patterns contain sufficient surface gradient texture for the solution to converge. Note that the strain precision in Fig. 4h is significantly higher than in Fig. 4g, and hence, for the following fibers, a pattern comparable to Fig. 4b is desired.

In conclusion, Fig. 4 confirms that the GDHC method works on rectangular viscose fibers, whereby severe particle clustering leads to increasing strain errors and second-order polynomials are sufficiently rich to capture the hygroscopic kinematics.

Fig. 4
figure 4

Experimental results of 3 different rectangular viscose fibers with: a–c each sprayed with a different pattern density of 1 \(\mu\)m particles and a zoomed in view showing the pattern quality, d–f mean residual versus relative humidity for polynomials of order 1–5 which shows that second-order polynomials are sufficiently rich to describe the fiber’s hygro-expansion behavior, and g–i the mean surface strain in longitudinal and transverse directions as a function of the relative humidity during two wetting cycles, which results in a pronounced difference in hygro-expansion response. Severe particle clustering (c) leads to higher residual values (note the different vertical scale in f), and consequently reduced precision of the strain data, whereas the pattern density in a is very sparse compared to typical high-quality DIC patterns (Dong and Pan 2017; Hoefnagels et al. 2019). Hence the pattern quality shown in b is to be preferred

Full size image

Next, Fig. 5a shows the topography and hygroscopic response of a trilobal viscose fiber. The fiber is tested with an objective of 100 \(\times\) and an FOV multiplier lens of 2 \(\times\), reducing the field of view to 30 \(\times\) 40 \(\mu\)m2, a vertical scanning range of 25 \(\mu\)m, resulting in a single topography scanning time of 12 s. The topography shows the horizontal lines of lost data due to sharp edges, which are also visible in Fig. 3b. Additionally, the zoomed in view shows the pattern quality for the mixture of 500 nm and 1 \(\mu\)m particles employed, to enhance the surface gradient. The hygroscopic strain response is comparable to that of Fig. 4. The release of a positive dried-in strain in longitudinal direction is a again visible. The hygroscopic strain data shows a rather good precision in both directions, hence confirming the quality of the applied pattern. In conclusion, the GDHC method is able to precisely capture the hygro-expansion of trilobal viscose fibers.

Figure 5b shows the topography and hygroscopic response of a 3D-printed hydrogel fiber. The fiber is tested with an objective of 100 \(\times\), a vertical scanning range of 25 \(\mu\)m. A pattern of both 500 nm and 1 \(\mu\)m particles is applied. The fiber is tested in two cycles, both starting from a relative humidity of 50 that increases to 90%. The fiber remains quasi-undeformed until a relative humidity of roughly 85% is reached, after which the fiber starts to swell rapidly to a large transverse surface strain of \(\sim\)0.25, with strain differences up to \(\sim\)1 × 10−2 between subsequent topography images (12 s). Additionally, this fiber shows a much larger increase in longitudinal direction compared to the previous fibers. In short, the GDHC method is also capable to precisely describe the hygro-expansion of 3D-printed hydrogel fibers, capturing large strain differences, i.e. \(\sim\)1 × 10−2 per topography.

Fig. 5
figure 5

Experimental results of a a trilobal viscose fiber and b 3D-printed hydrogel fiber, containing (left) a topography with zoom and (right) the mean surface strain in longitudinal and transverse directions versus relative humidity for two wetting cycles

Full size image

Finally, Fig. 6a shows the topography of a paper fiber. The fiber is tested with an objective of 100 \(\times\) and a FOV multiplier lens of 2 \(\times\), a vertical scanning range of 25 \(\mu\)m and a threshold of 10%. The topography directly shows the complications that emerge when testing natural fibers: areas of lost data due to transparency (in addition to the particles’ edges) and a highly irregular surface topography. The paper fiber is sprayed with both 500 nm and 1 \(\mu\)m particles, shown in the zoom. Since the main focus of this research lies on the exploitation of the GDHC method for natural fibers, which is the biggest challenge with respect to strain precision, this fiber is tested more extensively, i.e. subjected to a relative humidity cycle of 10–92–10–92%, as done in the analysis of the dynamic hygro-expansion of paper sheets in Larsson and Wågberg (2009). Additionally, the longitudinal, transverse and shear strain fields between the first and last image of the first relative humidity stage (10–92%) are given in Fig. 6b. The mean hygroscopic surface strain versus relative humidity response of the same first stage is given in Fig. 6c. A clear trend is visible; however, a large number of outliers, shown in gray, are present after a relative humidity of 60%. Due to an increase in the fiber’s transparency, more data is lost, which may deteriorate the GDHC method’s performance, for which the optimization solution may have converged to a local instead of the global minimum. Typically, the mean residuals of these presumed local minima are higher than the globally converged solutions. Hence, the mean residual of all data points after a relative humidity of 60% are given in a histogram in Fig. 6d, which shows a bimodal distribution, in which the peak at 0.142 \(\mu\)m corresponds to the global minimum solutions. To filter out the undesired local minima, i.e. the outliers from the low-residual peak, the standard deviation is determined. A data point is assumed to be an outlier if the mean residual exceeds 3\(\sigma\), thus only disregarding < 1% of the global minima as outlier. Figure 6e shows the mean hygroscopic strain in the two principal directions and the minor strain direction angle versus the relative humidity with the above determined outliers in gray. The minor strains are relatively constant around an angle of 5° from the longitudinal axis of the fiber, which seems to correspond to the micro-fibril angle that is known to influence the fiber swelling (Meylan 1972; Ek et al. 2009). This angle is in good agreement with the reported range of the MFA of this specific natural (Eucalyptus Globulus) fiber type (0°–13°), obtained by French et al. (2000) using confocal microscopy, where X-ray Diffraction, small angle X-ray scattering, wide angle X-ray scattering and polarization microscopy are additional techniques for determining the MFA (Donaldson 2008; Barnett and Bonham 2004). Choosing a different order polynomial can results in a slight change in the displacement field and hence in the angle of the principal strains. The hygroscopic surface strain response during the full relative humidity cycle, with the outliers in gray, is shown as a function of time in Fig. 6f. Note the negative transverse surface strain after the first drying stage. This indicates that a dried-in strain (due to manufacturing) is released after the first wetting stage, as observed for the viscose fibers, and reported at the paper sheet scale in Smith (1950), Salmén et al. (1987), Larsson and Wågberg (2009). Only an approximate comparison of the found strain values can be made with the literature because the literature values were obtained for different pulp fibers, while the moisture content was not logged in-situ. Nevertheless, a comparison could be made to the work of Meylan (1972), as the micro-fibril angle of 11.5° seems representative for our Eucalyptus Globulus fiber with a MFA of 0°–13° (Donaldson 2008), while the provided relative humidity to moisture content relation by Uesaka (2001) enables back-conversion to relative humidity. This yields a strain difference in longitudinal direction of  0.2% for a relative humidity change of 10–90%, which seems to be in good agreement with the longitudinal strain difference shown in Fig. 6c. In summary, the GDHC method can precisely track the hygro-expansion behavior of natural fibers with an irregular surface topography over a large testing range for both wetting and drying.

Fig. 6
figure 6

Experimental results of a eucalyptus paper fiber, containing: a topography with a zoomed in view for pattern evaluation, b longitudinal, transverse and shear strain fields between the first and last image of the first relative humidity stage (10–92%), c, d the mean surface strain in longitudinal and transverse directions versus the relative humidity (10–92%) and a histogram of the mean residual values to determine the outliers and reduce data noise, which are shown in gray in c, e the two principal strains and minor strain angle (estimation of the MFA) versus the relative humidity and f the mean surface strain in longitudinal and transverse directions during the applied relative humidity cycle (10–92–10–92%). The mean residual analysis, as presented in d is applied to reduce data noise and outliers

Full size image

Quantitative evaluation of the GDHC method

To quantify the potential of the proposed method, a precision analysis experiment is conducted, in which all six fibers (of four fiber types) are tested again. The relative humidity is kept constant (± 0.05%) for 100 topographies (\(\sim\)15 minutes) at, respectively, 50, 70 and 90%. Correlating these 100 height topographies allows quantification of the precision, by determining the standard deviation at the specified relative humidity values. All topographies are correlated to the undeformed initial topography at a relative humidity of 50%, to test the influence of fiber swelling on the precision.

Fig. 7
figure 7

Absolute surface strain precision quantification overview of the six tested fibers in both longitudinal and transverse direction at a relative humidity of respectively 50, 70 and 90%. A residual analysis for the paper fiber is conducted in the boxed area, in which the correlations with a mean residual exceeding 3\(\sigma\) are excluded from the data set, improving the precision, indicated by the black arrows

Full size image

Figure 7 shows the absolute surface strain precisions in longitudinal and transverse directions for all six fibers at respectively a relative humidity of 50, 70 and 90%. It is obvious that the precision in transverse direction is less good than in the longitudinal direction, which is consistent with the fact that more data points are available in longitudinal direction. For the rectangular viscose, the precision in longitudinal direction reduces with increasing particle clustering, while the best precision in transverse direction is achieved with a medium dense pattern. For the trilobal viscose fiber, the precision in transverse direction has increased compared to the flat viscose fiber, which is caused by the initial surface gradient of the fiber. For the 3D-printed hydrogel fiber, the GDHC method has a precision below 7 × 10−4 at a strain of roughly 0.25 in transverse direction, i.e. a relative precision of 2.8 × 10−3. Finally, for the paper fiber, the precision at 90% relative humidity in longitudinal direction directly stands out, which was also visible in Fig. 6. The same mean residual analysis is conducted as given in Fig. 6, to determine the outliers in the dataset. After removing these data points from the precision analysis, a corrected point is added in Fig. 7. This residual analysis significantly improves the longitudinal precision, while the transverse direction is only slightly improved, indicated by the black arrows.

Reconsidering Table 1, it can be concluded the precision of the proposed method, applied to a paper fibers, is at least one order of magnitude better in transverse direction and three times better in longitudinal direction compared to the other methods. However, this is compared to methods which were only able to measure the hygroscopic strain in one direction. Hence, when comparing to the method proposed by Lee et al. (2010), which is the only method able to measure both directions, the longitudinal strain precision is improved by two orders of magnitude, while in transverse direction the strain precision is improved by one order of magnitude. Additionally, the ease and applicability to a wide range of fiber types and sizes of the here-proposed method makes it very attractive, while AFM is usually labor intense with a limited FOV. Note that the method can be further improved by using a mistification setup (Shafqat submitted for publication) instead of an airbrush to obtain a dense and non-clustered pattern of particles.

Conclusion

A novel method has been developed and tested which allows continuous, full-field displacement measurements on a single fiber surface. The method consists of: (1) preparing the sample by delicately fixing a single fiber on a glass slide and, for the purpose of Global Digital Height Correlation (GDHC), applying a micro-particle pattern; (2) testing the fiber by changing the relative humidity around the fiber while taking consecutive topographies using an optical height microscope and; (3) processing the obtained topographies and analyzing them with an optimized GDHC algorithm using a second-order polynomial to obtain full-field displacement data of a fiber surface. A comprehensive derivation of the working principle behind GDHC is given while the importance of the applied pattern with adequate mean surface height gradients is demonstrated. Whereas the micro-particles provide surface height gradients, they inevitably also result in data loss around the edges, which leads to higher residual values in these regions. Therefore, an algorithm is introduced to dilate the pixel rows around each NaN pixel, for which an optimum dilatation of 2 rows is determined.

The developed method is subsequently tested on four types of fibers: (1) rectangular viscose fiber with a flat cross-section of 3 \(\times\) 50 \(\mu\)m\(^2\) and almost no surface roughness, (2) trilobal viscose fiber with a cross-section of 30 \(\mu\)m and some surface roughness, (3) 3D-printed hydrogel with a round cross-section of 50 \(\mu\)m, with limited surface roughness and a pronounced hygroscopic strain response and (4) eucalyptus paper fiber with a hollow ribbon-like cross-section of 35 \(\times\) 20 \(\mu\)m and high surface roughness. For the rectangular and the trilobal viscose fibers, the displacement field was successfully determined as long as the pattern quality was of reasonable quality, i.e. sufficient but no too high particle density. For the 3D-printed hydrogel, the proposed method was able to successfully capture the remarkable swelling behavior (strain differences of \(\sim\)1 × 10−2 between subsequent topographies). Finally, the eucalyptus paper fiber is tested, for which the hygroscopic strain is properly captured. However, at higher relative humidity values, both the noise and the degree of data loss in on the topographies significantly increases, caused by a strong increase in transparency as a result of the increase in moisture content of the fiber. This data quality reduction at high relative humidity challenges the conservation of surface height, which is the principle underlying GDIC, and may, therefore, induce convergence towards a local minimum instead of a global minimum. This problem is remedied by identifying data points with a high residual value (>3\(\sigma\)) as outliers to be removed from the dataset, thereby reducing the data noise and increasing the precision on paper fibers. The major to minor strain angle, obtained for full-field data, is in good agreement with the known range of micro-fibril angle (MFA) from the literature, which seems to indicate that the MFA can be determined with this method.

Finally, the above-described experiments have shown that the proposed method is at least one order of magnitude more precise than previously reported techniques, while the method is also fast, relatively simple, applicable to multiple fibers, allowing for full-field displacement measurements in both wetting and drying experiments.