On doubly symmetric periodic orbits

Abstract

In this article, for Hamiltonian systems with two degrees of freedom, we study doubly symmetric periodic orbits, i.e., those which are symmetric with respect to two (distinct) commuting antisymplectic involutions. These are ubiquitous in several problems of interest in mechanics. We show that, in dimension four, doubly symmetric periodic orbits cannot be negative hyperbolic. This has a number of consequences: (1) All covers of doubly symmetric orbits are good, in the sense of Symplectic Field Theory (Eliashberg et al. Geom Funct Anal Special Volume Part II:560–673, 2000); (2) a non-degenerate doubly symmetric orbit is stable if and only if its CZ-index is odd; (3) a doubly symmetric orbit does not undergo period doubling bifurcation; and (4) there is always a stable orbit in any collection of doubly symmetric periodic orbits with negative SFT-Euler characteristic (as coined in Frauenfelder et al. in Symplectic methods in the numerical search of orbits in real-life planetary systems. Preprint arXiv:2206.00627). The above results follow from: (5) A symmetric orbit is negative hyperbolic if and only its two B-signs (introduced in Frauenfelder and Moreno 2021) differ.

1 Introduction

This article deals with the study of doubly symmetric periodic orbits in dimension four, i.e., for Hamiltonian systems with two degrees of freedom. These are ubiquitous in problems of interest in mechanics; we give several examples in Sect. 2. Let us introduce the basic concepts.

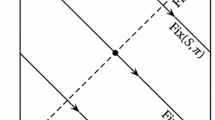
Symmetric orbits. Consider a symplectic manifold $(M,\omega )$ endowed with an antisymplectic involution $\rho : M\rightarrow M$ (i.e., $\rho ^2=id$, $\rho ^*=\omega =-\omega )$, also referred to as a real structure. Its fixed point set $L=\textrm{Fix}(\rho )$ is a Lagrangian submanifold of M. Given a Hamiltonian $H:M\rightarrow \mathbb R$, we say that $\rho$ is a symmetry of the Hamiltonian system induced by H, if $H\circ \rho =H$. In this situation, a symmetric periodic orbit is a periodic orbit $v: S^1=\mathbb R/\tau \mathbb R\rightarrow M$ satisfying $\rho (v(-t))=v(t)$ for all t. A symmetric periodic orbit can also be thought of as a chord starting and ending in L, where the endpoints coincide with $v(0), v(\tau /2)$ (the symmetric points), see Fig. 1.

Fig. 1

Left: a symmetric orbit. Right: a doubly symmetric orbit

Now, suppose we have two distinct antisymplectic involutions $\rho _1$ and $\rho _2$ which commute with each other. In this case, we have two Lagrangian submanifolds $L_1=\textrm{Fix}(\rho _1)$ and $L_2=\textrm{Fix}(\rho _2)$. Given a chord from $L_1$ to $L_2$, we can apply $\rho _2$ to it to get a chord from $L_1$ to itself. Now, apply $\rho _1$ to this chord. The resulting periodic orbit is then doubly symmetric, as it is symmetric with respect to both $\rho _1,\rho _2$, see again Fig. 1. We provide a more formal definition of the notion of a doubly symmetric periodic orbits in Sect. 4.

Reduced monodromy. Suppose that $(M,\omega )$ is a four-dimensional symplectic manifold, $H:M \rightarrow \mathbb {R}$ is a smooth Hamiltonian, and v is a non-constant periodic orbit of the Hamiltonian vector field $X_H$ of H of period $\tau$. By preservation of energy H is constant along v, i.e., v lies for all times on a level set $\Sigma =H^{-1}(c)$ for some $c \in \mathbb {R}$. The differential of the flow $\phi ^t_H$ induces a map on the two-dimensional quotient vector space

$$\begin{aligned}M_v:=\overline{d\phi ^\tau _H(v(0))} :T_{v(0)}\Sigma /\langle X_H(v(0))\rangle \rightarrow T_{v(0)}\Sigma /\langle X_H(v(0))\rangle ,\end{aligned}$$

referred to as the reduced monodromy. The reduced monodromy is a two-dimensional symplectic transformation, i.e., $\det M_v=1.$ Depending on the trace of its reduced monodromy, periodic orbits on a four-dimensional symplectic manifold are now partitioned into three classes.

Positive hyperbolic::

$\textrm{tr}(M_v)>2,$ in which case the reduced monodromy has two positive, real eigenvalues inverse to each other.

Negative hyperbolic::

$\textrm{tr}(M_v)<2,$ in which case the reduced monodromy has two negative, real eigenvalues inverse to each other.

Elliptic::

$-2\le \textrm{tr}(M_v)\le 2.$ If the trace is precisely two, the reduced monodromy has one as an eigenvalue with algebraic multiplicity two. If the trace is precisely minus two, it has minus one as an eigenvalue with algebraic multiplicity two. Otherwise it has two non-real eigenvalues on the unit circle conjugated to each other.

In the language of Symplectic Field Theory, an even cover of a negative hyperbolic orbit is called bad; otherwise, a periodic orbit is called good. Here, we prove the following:

Theorem A

For a Hamiltonian system with two degrees of freedom, a doubly symmetric periodic orbit cannot be negative hyperbolic.

In particular, it follows from Theorem A that all covers of a doubly symmetric periodic orbit are good periodic orbits.

Stability While elliptic periodic orbits are stable, hyperbolic ones are unstable. On the other hand, elliptic and negative hyperbolic orbits have odd Conley–Zehnder index, while positive hyperbolic ones have even Conley–Zehnder index. For the second statement, it is better to exclude the degenerate case where the trace of the reduced monodromy is two, since in this case there are different conventions on how to define the Conley–Zehnder index. We see from this that if we can exclude negative hyperbolic orbits, the question of stability of a periodic orbit can be answered in terms of the parity of its Conley–Zehnder index. In particular, we have the following corollary of Theorem A:

Corollary B

Suppose that v is a non-degenerate doubly symmetric periodic orbit of a Hamiltonian system with two degrees of freedom. Then, it is stable if and only if its Conley–Zehnder index is odd.

Overview of proof of Theorem A The proof of Theorem A uses a real version of Krein theory for the reduced monodromy of a symmetric periodic orbit. Given a symmetric orbit v, the differential of the antisymplectic involution at $v(0) \in L=\textrm{Fix}(\rho )$ induces an antisymplectic involution

$$\begin{aligned} R :T_{v(0)}\Sigma /\langle X_H(v(0))\rangle \rightarrow T_{v(0)}\Sigma /\langle X_H(v(0))\rangle , \end{aligned}$$

i.e., an orientation reversing involution on the two-dimensional vector space $T_{v(0)}\Sigma /\langle X_H$ (v(0)). The involution R conjugates the reduced monodromy with its inverse, i.e.,

$$\begin{aligned} RM_vR=M_v^{-1}. \end{aligned}$$

(1)

We choose a symplectic basis on $T_{v(0)}\Sigma /\langle X_H(v(0))$ such that the involution R gets identified with the matrix

$$\begin{aligned}R=\left( \begin{array}{cc} 1 &{} 0\\ 0 &{}-1 \end{array}\right) \end{aligned}$$

and the reduced monodromy is given by a matrix

$$\begin{aligned}M_v=\left( \begin{array}{cc} a &{} b\\ c &{} d \end{array}\right) \end{aligned}$$

satisfying the determinant condition $ad-bc=1$. It follows from (1) that $a=d$ so that

$$\begin{aligned}M_v=\left( \begin{array}{cc} a &{} b\\ c &{} a \end{array}\right) , \quad a^2-bc=1.\end{aligned}$$

In particular, the question to which class the periodic orbit belongs is completely answered by the entry a of the reduced monodromy matrix. For fixed a, if an off-diagonal entry is not zero, then it completely determines the other one in view of the determinant condition. On the other hand, the off-diagonal entries depend on the choice of the symplectic basis used to identify the reduced monodromy with a matrix. Since the symplectic basis vectors are required to be eigenvectors of the antisymplectic involution R, such a symplectic basis is determined up to a scaling factor, so that the identification of the reduced monodromy with a matrix is unique up to conjugation by a matrix of the form

$$\begin{aligned}\left( \begin{array}{cc} \mu &{} 0\\ 0 &{} \frac{1}{\mu } \end{array}\right) , \quad \mu \in \mathbb {R}\setminus \{0\}.\end{aligned}$$

In particular, while the value of b is not an invariant, its sign is an invariant. Following (Frauenfelder and Moreno 2021), we refer to $\textrm{sign}(b)$ as the B-sign of the reduced monodromy, see also (Zhou 2022). In the case elliptic case, by (Frauenfelder and Moreno 2021, Appendix B), the B-sign gives the same information as the Krein type of the eigenvalues of the reduced monodromy (as introduced in (Krein 1950, 1951a, b, c; Moser 1958)). In the hyperbolic case, the eigenvalues have no Krein type. Therefore, the B-sign in the hyperbolic case is an additional invariant of the real structure $\rho$.

A symmetric periodic orbit intersects the Lagrangian $L=\textrm{Fix}(\rho )$ in its two symmetric points. From the reduced monodromies of each symmetric point, we obtain a B-sign, so that a symmetric periodic orbit is actually endowed with two B-signs. The main observation to prove Theorem A is the following:

Theorem C

A symmetric periodic orbit of a Hamiltonian system with two degrees of freedom is negative hyperbolic if and only if its two B-signs are different.

If the symmetric periodic orbit is elliptic, it is actually clear that the two B-signs have to agree. Indeed, as already mentioned, in the elliptic case the B-sign is just determined by the Krein sign of the eigenvalues. Since reduced monodromy matrices of a periodic orbit for different starting points are all conjugated to each other, Theorem C follows in the elliptic case. What remains to be examined is the hyperbolic case, namely that in the positive hyperbolic case the two B-signs agree, while in the negative hyperbolic case they disagree. To address this, in Sect. 3 we introduce the notion of real couples, so that Theorem C becomes a consequence of Proposition 3.2.

The strategy to prove Theorem A is now rather obvious. One shows that the additional real structure for a doubly symmetric periodic orbit forces the two B-signs to agree, so that, in view of Theorem C, a doubly periodic orbit cannot be negative hyperbolic. This is carried out in Sect. 5 where Theorem A is referred to as Corollary 5.1.

Period doubling bifurcation. When considered in families, periodic orbits may undergo bifurcation, by which a non-degenerate orbit becomes degenerate (i.e., 1 becomes an eigenvalue of its monodromy), and new orbits may appear. Generic bifurcations in dimension four are well understood, see, e.g., (Abraham and Marsden 1978, p. 599). However, the presence of symmetry, and in particular the presence of doubly symmetric orbits, is non-generic, and hence, one expects new phenomena. And indeed, what follows aligns well with this expectation.

As a particular case of bifurcations, the transition from an elliptic periodic orbit to a negative hyperbolic orbit leads to a period doubling bifurcation, by which a new orbit appears, whose period is close to double the period of the original orbit. In the case, where the negative hyperbolic orbit is symmetric, its two different B-signs can actually be useful to figure out where the new periodic orbit of double period bifurcates, see (Frauenfelder et al. 2022). Namely, bifurcation happens near the symmetric point where the B-sign does not jump. Moreover, a consequence of Theorem A is the following, which emphasizes the non-generic nature of symmetry:

Corollary D

In dimension four, doubly symmetric periodic orbits do not undergo period doubling bifurcation.

Indeed, as in period doubling bifurcation the orbit itself does not bifurcate (its double cover does), the orbit after such a bifurcation would have to be doubly symmetric if the orbit before bifurcation is, thus contradicting Theorem A. We remark that Corollary D fails in dimension six, i.e., for systems with three degrees of freedom. Indeed, see, e.g., (Frauenfelder et al. 2022, Section 6) for a numerical example of a planar-to-spatial period doubling bifurcation of doubly symmetric orbits.

SFT-Euler characteristic. In order to address the situation of more general bifurcations than period doubling bifurcation (in the presence of symmetry), we consider a Floer numerical invariant. Namely, following (Frauenfelder and Moreno 2021), the SFT-Euler characteristic of a periodic orbit v is by definition the Euler characteristic of its local Floer homology, given by

$$\begin{aligned} \chi _{SFT}(v)=\#\{\text{ good } \text{ positive } \text{ hyperbolic }\}-\#\{\text{ elliptic, } \text{ negative } \text{ hyperbolic }\}. \end{aligned}$$

Here, one counts each type of orbit that appears after a generic perturbation of the orbit v, so that it bifurcates into a collection of non-degenerate orbits. We remark that bad orbits do not contribute to this number. Note also that this number is $\pm 1$ in the case where v is itself non-degenerate, depending on its type. The remarkable fact, which follows from Floer theory, is that $\chi _{SFT}(v)$ is independent of the perturbation, and so in particular it remains invariant under bifurcations of v. It is therefore very useful in order to study non-generic bifurcations.

Moreover, given a collection of periodic orbits (which may not necessarily arise from a bifurcation, but, e.g., as critical points of an action functional, with a priori fixed homotopy class) one can also consider the same number computed via the above formula. Its invariance under arbitrary homotopies will of course not be guaranteed and will depend on the particular situation. An example of interest, for which a suitable homotopy invariance holds, is frozen planets. These are periodic orbits for the Helium problem which we discuss in more detail in Sect. 2. Due to the interaction between the two electrons in Helium, frozen planets cannot be approached by perturbative methods but instead one can replace the instantaneous interaction of the two electrons by a mean interaction. If one interpolates between mean and instantaneous interaction, one obtains a homotopy of a frozen planet problem for which one has compactness in the symmetric case (Frauenfelder 2020). This allows one to define a version of the Euler characteristic for frozen planets which is invariant under this homotopy (Cieliebak et al. 2022), and which agrees with the SFT-Euler characteristic $\chi _{SFT}$ for the instantaneous interaction. The Euler characteristic for this problem is $-1$, see the remark after Corollary B in Cieliebak et al. (2022). For each negative energy, this implies the existence of a symmetric frozen planet orbit for the instantaneous interaction, see Corollary C in Cieliebak et al. (2022). This follows by homotopy invariance of the Euler characteristic, and the existence (proved analytically in Frauenfelder 2021) of a unique non-degenerate symmetric orbit for the mean interaction.

With these motivations in mind, the following is again a consequence of Theorem A:

Corollary E

In dimension four, suppose that a collection of doubly symmetric periodic orbits has negative SFT-Euler characteristic. Then, a stable periodic orbit exists.

Indeed, Theorem A and the formula defining $\chi _{SFT}$ imply the existence of an elliptic orbit, and one needs to recall that elliptic orbits are precisely the stable orbits for a Hamiltonian system in dimension four.

2 Examples of doubly symmetric periodic orbits

2.1 The direct and retrograde periodic orbit in Hill’s lunar problem

Hill’s lunar Hamiltonian goes back to Hill’s groundbreaking work on the orbit of our Moon (Hill 1878), describing its motion around the Earth and the Sun. The Earth lies in the center of the frame of reference, while the Sun, assumed to be infinitely much heavier than the Earth, lies at infinity. The Hamiltonian reads

$$\begin{aligned}H :T^*(\mathbb {R}^2 \setminus \{0\}) \rightarrow \mathbb {R}, \quad (q,p) \mapsto \frac{1}{2}\big ((p_1+q_2)^2+(p_2-q_1)^2\big ) -\frac{1}{|q|}-\frac{3}{2}q_1^2.\end{aligned}$$

It is invariant under the two commuting antisymplectic involutions

$$\begin{aligned}\rho _1, \rho _2 :T^*\mathbb {R}^2 \rightarrow T^*\mathbb {R}^2\end{aligned}$$

given, for $(q,p) \in T^*\mathbb {R}^2$, by

$$\begin{aligned}\rho _1(q_1,q_2,p_1,p_2)=(q_1,-q_2,-p_1,p_2), \quad \rho _2(q_1,q_2,p_1,p_2)=(-q_1,q_2,p_1,-p_2).\end{aligned}$$

The fixed point sets of the two antisymplectic involutions are the conormal bundles of the x-axis and the y-axis, respectively. If one studies a doubly symmetric periodic orbit in configuration space $\mathbb {R}^2 \setminus \{0\}$, this means that it starts perpendicularly at the x-axis, after a quarter period hits the y-axis perpendicularly, then gets reflected at the y-axis for the next quarter period, and finally gets reflected at the x-axis for the second half of the period. Such periodic orbits can be found by a shooting argument where one shoots perpendicularly from the x-axis for a varying starting point at the x-axis, until one hits the y-axis perpendicularly. Birkhoff used in Birkhoff (1915) this shooting argument to prove the existence of the retrograde periodic orbit for all energies below the first critical value, see also (Frauenfelder and van Koert 2018, Chapter 8.3.2). Although the retrograde periodic orbit looks simpler than the direct one (Hénon 1969), astronomers are actually often more interested in the direct one, since our Moon and actually most moons in our solar system are direct. However, there are prominent counterexamples. Triton, the largest moon of the planet Neptune, is, for example, retrograde.

2.2 The Levi-Civita regularization

Hill’s lunar problem arises as a limit case of the restricted three-body problem, see, for instance, (Frauenfelder and van Koert 2018, Chapter 5.8.2). In the restricted three-body problem, the masses of the Sun and the Earth are comparable and their distance is finite. Different from the Hill’s lunar problem, the restricted three-body problem is only invariant under the antisymplectic involution

$$\begin{aligned}\rho :T^* \mathbb {R}^2 \rightarrow T^* \mathbb {R}^2, \quad (q_1,q_2,p_1,p_2) \mapsto (q_1,-q_2,-p_1,p_2)\end{aligned}$$

obtained from reflection at the x-axis, but not anymore under the antisymplectic involution corresponding to reflection at the y-axis.

We identify $\mathbb {R}^2$ with the complex plane $\mathbb {C}$ and denote by $\mathbb {C}^*:=\mathbb {C} \setminus \{0\}$ the complex plane pointed at the origin. We consider the squaring map

$$\begin{aligned}\ell :\mathbb {C}^* \rightarrow \mathbb {C}^*, \quad z \mapsto z^2.\end{aligned}$$

Note that the squaring map is a two-to-one covering. The contragradient (or symplectic lift) of the squaring map is the symplectic map

$$\begin{aligned}L :T^* \mathbb {C}^* \rightarrow T^*\mathbb {C}^*, \quad (z,w) \mapsto \bigg (z^2, \frac{w}{2\bar{z}}\bigg ),\end{aligned}$$

where $\bar{z}$ is the complex conjugate of z. This map was used by Levi-Civita to regularize two-body collisions (Levi-Civita 1920), and therefore, it is known under the name of Levi-Civita regularization. On $T^* \mathbb {C}$, we have the two commuting antisymplectic involutions

$$\begin{aligned}\sigma _1,\sigma _2 :T^* \mathbb {C} \rightarrow T^*\mathbb {C}\end{aligned}$$

which are given, for $(z,w) \in \mathbb {C} \times \mathbb {C}=T^*\mathbb {C}$, by

$$\begin{aligned}\sigma _1(z,w)=(\bar{z},-\bar{w}), \quad \sigma _2(z,w)=(-\bar{z},\bar{w}).\end{aligned}$$

The Levi-Civita regularization lifts the restriction of the antisymplectic involution $\rho$ to $T^* \mathbb {C}^*$ to the restriction of $\sigma _1$ and $\sigma _2$ to $T^*\mathbb {C}^*$, so that we have

$$\begin{aligned}L \circ \sigma _1\big |_{T^*\mathbb {C}^*}=\rho \big |_{T^*\mathbb {C}^*} \circ L, \qquad L \circ \sigma _2\big |_{T^*\mathbb {C}^*}=\rho \big |_{T^*\mathbb {C}^*} \circ L.\end{aligned}$$

Now, suppose that $v=(q,p)$ is a periodic orbit in $T^*\mathbb {C}^*$ which is symmetric with respect to $\rho$, and such that it has odd winding number around the origin. Then, v lifts under the Levi-Civita regularization to a periodic orbit on $T^*\mathbb {C}^*$ which is doubly symmetric with respect to $\sigma _1$ and $\sigma _2$.

On the other hand, retrograde and direct orbits exist as well in the restricted three-body problem. Different from Hill’s lunar problem, they are just symmetric, but not doubly symmetric. However, the lifts under the Levi-Civita regularization are doubly symmetric, as the retrograde and direct periodic orbit have winding number one around the origin.

2.3 Langmuir’s periodic orbit

Langmuir’s periodic orbit is a periodic orbit for the Helium problem. It was first discovered by Langmuir (1921) numerically as a candidate for the ground state of the Helium atom. For an analytic existence proof, we refer to Cieliebak et al. (2022), and for its role in the semiclassical treatment of Helium, to Tanner et al. (2000).

In the Helium atom, there is a nucleus of positive charge plus two at the origin, i.e., there are two protons. It attracts two electrons of charge minus one according to Coulomb’s law, which looks formally the same as Newton’s law. Moreover, the two electrons repel each other, again according to Coulomb’s law. We abbreviate by

$$\begin{aligned}\Delta :=\big \{(q,q): q \in \mathbb {C}^*\big \} \subset \mathbb {C}^* \times \mathbb {C}^*\end{aligned}$$

the diagonal. The Hamiltonian for the planar Helium problem is then a smooth function

$$\begin{aligned}H :T^*\big (\mathbb {C}^* \times \mathbb {C}^* \setminus \Delta \big ) \rightarrow \mathbb {R}\end{aligned}$$

given by

$$\begin{aligned}H(q_1,q_2,p_1,p_2)=\frac{1}{2}|p_1|^2+\frac{1}{2}|p_2|^2-\frac{2}{|q_1|} -\frac{2}{|q_2|}+\frac{1}{|q_1-q_2|}.\end{aligned}$$

Fig. 2

Langmuir’s doubly symmetric orbit and its symmetric version

The Hamiltonian is invariant under the symplectic involution

$$\begin{aligned}\sigma :T^*\big (\mathbb {C}^* \times \mathbb {C}^* \setminus \Delta \big ) \rightarrow T^*\big (\mathbb {C}^* \times \mathbb {C}^* \setminus \Delta \big )\end{aligned}$$

given by

$$\begin{aligned}\sigma (q_1,q_2,p_1,p_2)=(\bar{q}_2,\bar{q}_1,\bar{p}_2,\bar{p}_1),\end{aligned}$$

consisting of the combination of particle interchange and reflection at the x-axis. The Langmuir Hamiltonian is the restriction of H to the fixed point set of $\sigma$

$$\begin{aligned}H_\sigma :=H\big |_{\textrm{Fix}(\sigma )} :\textrm{Fix}(\sigma ) \rightarrow \mathbb {R}.\end{aligned}$$

The fixed points set consists of points $(q_1,q_2,p_1,p_2) \in T^*(\mathbb {C}^* \times \mathbb {C}^* {\setminus } \Delta )$ which satisfy

$$\begin{aligned}q_1=\bar{q}_2=:q, \quad p_1=\bar{p}_2=:p.\end{aligned}$$

It therefore suffices to consider the Langmuir Hamiltonian on the cotangent bundle of the upper half plane

$$\begin{aligned}\mathbb {H}=\big \{q=q_1+iq_2 \in \mathbb {C}: q_2>0\big \}\end{aligned}$$

where it is given by

$$\begin{aligned}H_\sigma (q,p)=|p|^2-\frac{4}{|q|}+\frac{1}{2q_2}.\end{aligned}$$

On the cotangent bundle of the upper half plane, we have the two antisymplectic involutions

$$\begin{aligned}\rho _1,\rho _2 :T^* \mathbb {H} \rightarrow T^*\mathbb {H}\end{aligned}$$

given by

$$\begin{aligned}\rho _1(q,p)=(-\bar{q},\bar{p}), \quad \rho _2(q,p)=(q,-p),\end{aligned}$$

under both of which $H_\sigma$ is invariant. The fixed point set of $\rho _1$ is the conormal bundle of the positive imaginary axis, while the fixed point set of $\rho _2$ consists of brake points, i.e., at which the velocity is zero. The Langmuir orbit for the first electron $e_1^-$ starts perpendicularly at the imaginary axis and brakes at a quarter of the period and is therefore a doubly symmetric periodic orbit with respect to $\rho _1$ and $\rho _2$. The second electron $e_2^-$ similarly has an associated Langmuir orbit, obtained by conjugation of that of $e_1^-$, see Fig. 2.

2.4 Symmetric frozen planets

Other examples of periodic orbits for the Helium problem are frozen planet orbits. In this examples, both electrons lie on a line on the same side of the nucleus. The inner electron makes consecutive collisions with the nucleus. The outer electron, the actual “frozen planet,” which is attracted by the nucleus but repelled by the inner electron, stays almost stationary but liberates slightly. Frozen planet orbits were discovered by physicists (Tanner et al. 2000; Wintgen et al. 1993) in the context of semiclassics. They recently attracted the interest of mathematicians (Cieliebak et al. 2022; Zhao 2023). A frozen planet orbit is called symmetric if the two electrons brake at the same time, and at the time, the inner electron collides with the nucleus the outer electron brakes again, see Fig. 3. If one applies the Levi–Civita regularization to a symmetric frozen planet, one obtains a doubly symmetric periodic orbit.

Fig. 3

A frozen planet configuration

3 Real couples

A real symplectic vector space is a triple $(V,\omega ,R)$ consisting of a symplectic vector space $(V,\omega )$ and a linear antisymplectic involution $R :V \rightarrow V$, i.e., $R^2=Id, R^*\omega =-\omega$.

Definition 3.1

Assume that $(V_1,\omega _1,R_1)$ and $(V_2,\omega _2,R_2)$ are real symplectic vector spaces. A real couple $(\Psi ,\Phi )$ is a tuple of linear symplectic maps

$$\begin{aligned}\Psi :(V_1,\omega _1) \rightarrow (V_2,\omega _2), \quad \Phi :(V_2,\omega _2) \rightarrow (V_1,\omega _1)\end{aligned}$$

which are related by

$$\begin{aligned} R_2 \Psi R_1=\Phi ^{-1}. \end{aligned}$$

(2)

Note that if $(\Psi ,\Phi )$ is a real couple, then $(\Phi ,\Psi )$ is one as well, since it follows from (2) that

$$\begin{aligned}R_1 \Phi R_2=R_1 R_1^{-1} \Psi ^{-1} R_2^{-1}R_2=\Psi ^{-1}.\end{aligned}$$

If $(\Psi ,\Phi )$ is a real couple, then its composition

$$\begin{aligned}\Phi \Psi :(V_1,\omega _1) \rightarrow (V_1,\omega _1)\end{aligned}$$

is a linear symplectic map from the fixed symplectic vector space $(V_1,\omega _1)$ into itself which has the special property that it is conjugated to its inverse via the antisymplectic involution $R_1$. Indeed,

$$\begin{aligned} R_1 \Phi \Psi R_1= & {} R_1 \Phi R_2 R_2 \Psi R_1=\Psi ^{-1} \Phi ^{-1}=(\Phi \Psi )^{-1}. \end{aligned}$$

(3)

We now consider more closely the two-dimensional case. Note that every two-dimensional real symplectic vector space is conjugated to $\mathbb {R}^2$, endowed with its standard symplectic structure and antisymplectic involution

$$\begin{aligned}R=\left( \begin{array}{cc} 1 &{} 0\\ 0 &{} -1 \end{array}\right) .\end{aligned}$$

After such conjugation, a real couple then consists of a pair of matrices

$$\begin{aligned}(A,B) \in SL(2;\mathbb {R}) \times SL(2;\mathbb {R})\end{aligned}$$

such that

$$\begin{aligned} RAR=B^{-1}. \end{aligned}$$

(4)

Writing

$$\begin{aligned}A=\left( \begin{array}{cc} a &{} b\\ c &{} d \end{array}\right) , \quad ad-bc=1\end{aligned}$$

we have

$$\begin{aligned} RAR= & {} \left( \begin{array}{cc} 1 &{} 0\\ 0 &{} -1 \end{array}\right) \left( \begin{array}{cc} a &{} b\\ c &{} d \end{array}\right) \left( \begin{array}{cc} 1 &{} 0\\ 0 &{} -1 \end{array}\right) \\= & {} \left( \begin{array}{cc} 1 &{} 0\\ 0 &{} -1 \end{array}\right) \left( \begin{array}{cc} a &{} -b\\ c &{} -d \end{array}\right) \\= & {} \left( \begin{array}{cc} a &{} -b\\ -c &{} d \end{array}\right) \end{aligned}$$

and therefore

$$\begin{aligned}B=(RAR)^{-1}=\left( \begin{array}{cc} d &{} b\\ c &{} a \end{array}\right) .\end{aligned}$$

Hence, their products are given by the following matrices

$$\begin{aligned} AB=\left( \begin{array}{cc} a &{} b\\ c &{} d \end{array}\right) \left( \begin{array}{cc} d &{} b\\ c &{} a \end{array}\right) =\left( \begin{array}{cc} ad+bc &{} 2ab\\ 2cd &{} ad+bc \end{array}\right) \end{aligned}$$

(5)

and

$$\begin{aligned} BA=\left( \begin{array}{cc} d &{} b\\ c &{} a \end{array}\right) \left( \begin{array}{cc} a &{} b\\ c &{} d \end{array}\right) =\left( \begin{array}{cc} ad+bc &{} 2bd\\ 2ac &{} ad+bc \end{array}\right) . \end{aligned}$$

(6)

Since

$$\begin{aligned}BA=B(AB)B^{-1}\end{aligned}$$

, the two products are conjugated to each other in $SL(2;\mathbb {R})$. Moreover, they both belong to the subspace

$$\begin{aligned}SL^R(2;\mathbb {R}):=\Bigg \{M=\left( \begin{array}{cc} \alpha &{} \beta \\ \gamma &{} \alpha \end{array}\right) : \alpha ^2-\beta \gamma =1\Bigg \}\end{aligned}$$

of $SL(2;\mathbb {R})$. If $M \in SL^R(2;\mathbb {R})$ satisfies $\textrm{tr}(M) \ne \pm 2$, we define its real Krein sign as

$$\begin{aligned}\kappa (M):=\textrm{sign}(\beta ).\end{aligned}$$

Note that the trace condition implies that $\alpha \ne \pm 1$ so that, in view of the determinant condition $\alpha ^2-\beta \gamma$, we have that $\beta \ne 0$, and so its sign is well defined. The following proposition is now straightforward to prove.

Proposition 3.2

The real Krein signs of AB and BA differ, if and only if

$$\begin{aligned} \textrm{tr}(AB)=\textrm{tr}(BA)<-2, \end{aligned}$$

(7)

i.e., if and only if AB and therefore as well BA are negative hyperbolic.

Proof

By (5) and (6), the trace condition (7) is equivalent to the inequality

$$\begin{aligned}ad+bc<-1.\end{aligned}$$

In view of the determinant condition $ad-bc=1$, this in turn is equivalent to the inequality

$$\begin{aligned}ad<0,\end{aligned}$$

i.e., the requirement that the signs of a and d are different. Having once more a look at (5) and (6), we see that this happens if and only if the real Krein signs of AB and BA disagree. This proves the proposition. $\square$

In the following, we assume that $(\Psi ,\Phi )$ is a real couple between real symplectic vector spaces $(V_1,\omega _1,R_1)$ and $(V_2,\omega _2,R_2)$.

Definition 3.3

The real couple $(\Psi ,\Phi )$ is called symmetric if there exists a linear map

$$\begin{aligned}S :V_1 \rightarrow V_2\end{aligned}$$

which is antisymplectic, i.e.,

$$\begin{aligned}S^* \omega _2=-\omega _1\end{aligned}$$

and satisfies

$$\begin{aligned} \Psi =S\Psi ^{-1}S, \quad \Phi ^{-1}=S\Phi S, \quad R_2 S R_1=S. \end{aligned}$$

(8)

For a symmetric real couple

$$\begin{aligned}T:=SR_1=R_2 S :(V_1,\omega _1) \rightarrow (V_2,\omega _2)\end{aligned}$$

is a linear symplectic map which in view of

$$\begin{aligned}TR_1=S=R_2 T\end{aligned}$$

interchanges the two real structures, so that T leads to an identification of the two real symplectic vector spaces $(V_1,\omega _1,R_1)$ and $(V_2,\omega _2,R_2)$. In the two-dimensional case, if we identify this further with $\mathbb {R}^2$ endowed with its standard symplectic form and standard real structure R, then not only $R_1$ and $R_2$ are identified with R, but so is S. The real tuple becomes identified with a pair (A, B) of $SL(2,\mathbb {R})$-matrices which not only satisfy (4) but due to (8) also satisfy

$$\begin{aligned}RAR=A^{-1}, \qquad RBR=B^{-1},\end{aligned}$$

i.e., both matrices are conjugated to their inverse via R and therefore lie in the subspace $SL^R(2;\mathbb {R})$ of $SL(2;\mathbb {R})$. This implies that

$$\begin{aligned}A=B=\left( \begin{array}{cc} a &{} b\\ c &{} a \end{array}\right) ,\quad a^2-bc=1\end{aligned}$$

and therefore

$$\begin{aligned}AB=BA.\end{aligned}$$

In particular, AB and BA have the same real Krein sign. Therefore, we obtain the following corollary from Proposition 3.2.

Corollary 3.4

Suppose that $(\Psi ,\Phi )$ is a two-dimensional symmetric real couple. Then, neither $\Phi \Psi$ nor $\Psi \Phi$ are negative hyperbolic.

4 Doubly symmetric periodic orbits

Suppose that $(M,\omega )$ is a symplectic manifold and $H :M \rightarrow \mathbb {R}$ is a smooth Hamiltonian. The Hamiltonian vector field $X_H$ of H is implicitly defined by the condition

$$\begin{aligned}dH=\omega (\cdot , X_H).\end{aligned}$$

We abbreviate by $S^1=\mathbb {R}/\mathbb {Z}$ the circle. A simple periodic orbit is a bijective map $v :S^1 \rightarrow \mathbb {R}$ for which there exists $\tau >0$ such that v solves the ODE

$$\begin{aligned}\partial _t v(t)=\tau X_H(v(t)), \quad t \in S^1.\end{aligned}$$

Since for a simple periodic orbit the map is bijective, the Hamiltonian vector field $X_H$ is non-vanishing along v and therefore $\tau$ is uniquely determined by v. We refer to $\tau$ as the period of the simple periodic orbit v. We abbreviate by

$$\begin{aligned}\mathcal {P}_H \subset C^\infty (S^1,M)\end{aligned}$$

the set of simple periodic orbits of the Hamiltonian vector field $X_H$.

A real symplectic manifold is a triple $(M,\omega ,\rho )$ where $(M,\omega )$ is a symplectic manifold and $\rho \in \textrm{Diff}(M)$ is an antisymplectic involution on M, i.e.,

$$\begin{aligned}\rho ^2=\textrm{id}, \quad \rho ^* \omega =-\omega .\end{aligned}$$

If $H :M \rightarrow \mathbb {R}$ is a smooth function on a real symplectic manifold which is invariant under the antisymplectic involution, i.e.,

$$\begin{aligned}H \circ \rho =H,\end{aligned}$$

then its Hamiltonian vector field is anti-invariant, i.e.,

$$\begin{aligned}\rho ^*X_H=-X_H.\end{aligned}$$

We then obtain an involution

$$\begin{aligned}I :\mathcal {P}_H \rightarrow \mathcal {P}_H, \quad v \mapsto \rho \circ v^-\end{aligned}$$

where $v^-$ is the orbit traversed backward, i.e.,

$$\begin{aligned}v^-(t)=v(-t), \quad t \in S^1.\end{aligned}$$

A simple symmetric periodic orbit is a fixed point of I, i.e., $v \in \mathcal {P}_H$ satisfying

$$\begin{aligned}I(v)=v.\end{aligned}$$

We abbreviate by

$$\begin{aligned}\mathcal {P}^I_H:=\textrm{Fix}(I) \subset \mathcal {P}_H\end{aligned}$$

the set of simple symmetric periodic orbits. We remark that the fixed point set of an antisymplectic involution

$$\begin{aligned}L:=\textrm{Fix}(\rho )\end{aligned}$$

is a Lagrangian submanifold of M. Note that if $v \in \mathcal {P}^I_H$, then

$$\begin{aligned}v\big (0\big ), v\big (\tfrac{1}{2}\big ) \in L\end{aligned}$$

so that $v_{[0,\frac{1}{2}]}$ can be interpreted as a chord from L to L.

A doubly real symplectic manifold is a quadruple $(M,\omega ,\rho _1,\rho _2)$ where $(M,\omega )$ is a symplectic manifold and $\rho _1, \rho _2 \in \textrm{Diff}(M)$ are two distinct antisymplectic involutions which commute with each other. Note since $\rho _1$ and $\rho _2$ commute their composition

$$\begin{aligned}\sigma :=\rho _1 \circ \rho _2=\rho _2 \circ \rho _1\end{aligned}$$

is a symplectic involution on $(M,\omega )$. Suppose that $(M,\omega ,\rho _1,\rho _2)$ is a doubly real symplectic manifold and $H :M \rightarrow \mathbb {R}$ is a smooth map which is invariant under both involutions $\rho _1$ and $\rho _2$. We then have on the set of simple periodic orbits $\mathcal {P}_H$ two involutions

$$\begin{aligned}I_1 :\mathcal {P}_H \rightarrow \mathcal {P}_H, \quad v \mapsto \rho _1 \circ v^-, \qquad I_2 :\mathcal {P}_H \rightarrow \mathcal {P}_H, \quad v \mapsto \rho _2 \circ v^-.\end{aligned}$$

Moreover, we have two Lagrangian submanifolds of M

$$\begin{aligned}L_1=\textrm{Fix}(\rho _1), \qquad L_2=\textrm{Fix}(\rho _2).\end{aligned}$$

Definition 4.1

Suppose that $(M,\omega ,\rho _1,\rho _2)$ is a doubly real symplectic manifold and $H :M \rightarrow \mathbb {R}$ is a smooth function invariant under both involutions $\rho _1$ and $\rho _2$. A simple symmetric periodic orbit $v \in \mathcal {P}^{I_1}_H$ of $\rho _1$ is called doubly symmetric if

$$\begin{aligned} \rho _2 \circ v\big (0\big )=v\big (\tfrac{1}{2}\big ). \end{aligned}$$

(9)

Observe that since for a symmetric periodic orbit v(1/2) lies in the fixed point set of $\rho _1$ condition (9) is equivalent to

$$\begin{aligned}\sigma \circ v\big (0\big )=v\big (\tfrac{1}{2}\big ).\end{aligned}$$

Doubly symmetric periodic orbits with respect to $\rho _1$ are in natural one-to-one correspondence with doubly symmetric periodic orbits with respect to $\rho _2$. For $r \in S^1$ and $v \in \mathcal {P}_H$, we denote by

$$\begin{aligned}r_*v \in \mathcal {P}_H\end{aligned}$$

the reparametrized simple periodic orbit

$$\begin{aligned}r_*v (t)=v(r+t), \quad t \in S^1.\end{aligned}$$

We have the following lemma.

Lemma 4.2

An orbit $v \in \mathcal {P}_H^{I_1}$ is doubly symmetric with respect to $\rho _2$ if and only if $\big (\tfrac{1}{4}\big )_*v \in \mathcal {P}_H^{I_2}$ is doubly symmetric with respect to $\rho _1$.

Proof

Suppose that $v \in \mathcal {P}_H^{I_1}$ is doubly symmetric with respect to $\rho _2$. After reparametrization, a simple periodic orbit is still a simple periodic orbit so that we have

$$\begin{aligned}\big (\tfrac{1}{4}\big )_* v \in \mathcal {P}_H.\end{aligned}$$

Since H is invariant under $\rho _2$, we have that

$$\begin{aligned}I_2 \Big (\big (\tfrac{1}{4}\big )_* v\Big ) \in \mathcal {P}_H.\end{aligned}$$

Using (9), we compute

$$\begin{aligned} I_2 \Big (\big (\tfrac{1}{4}\big )_* v\Big )\big (\tfrac{1}{4}\big )= & {} \rho _2 \circ \Big (\big (\tfrac{1}{4}\big )_* v\Big )^-\big (\tfrac{1}{4}\big )\\= & {} \rho _2\Big (\big (\tfrac{1}{4}\big )_*v\Big )\big (-\tfrac{1}{4}\big )\\= & {} \rho _2 \circ v\big (\tfrac{1}{4}-\tfrac{1}{4}\big )\\= & {} \rho _2 \circ v(0)\\= & {} v\big (\tfrac{1}{2}\big )\\= & {} \Big (\big (\tfrac{1}{4}\big )_*v\Big )\big (\tfrac{1}{4}\big ). \end{aligned}$$

That means that $\big (\tfrac{1}{4}\big )_*v$ and $I_2\big (\big (\tfrac{1}{4}\big )_*v\big )$ are solutions of the same first-order ODE which at time $\tfrac{1}{4}$ go through the same point. Therefore, from the uniqueness of the initial value problem of first-order ODEs we deduce that

$$\begin{aligned}I_2\Big (\big (\tfrac{1}{4}\big )_*v\Big )=\big (\tfrac{1}{4}\big )_*v\end{aligned}$$

and hence

$$\begin{aligned}\big (\tfrac{1}{4}\big )_*v \in \mathcal {P}^{I_2}_H.\end{aligned}$$

It remains to check its double symmetry with respect to $\rho _1$. For that, we compute

$$\begin{aligned} \rho _1 \circ \Big (\big (\tfrac{1}{4}\big )_* v\Big )(0)= & {} \rho _1 \circ v\big (\tfrac{1}{4}\big )\\= & {} v\big (-\frac{1}{4}\big )\\= & {} v\big (\tfrac{3}{4}\big )\\= & {} \Big (\big (\tfrac{1}{4}\big )_*v\Big )\big (\tfrac{1}{2}\big ). \end{aligned}$$

Here, we have used in the second equation that v is symmetric with respect to $\rho _1$ and in the third equation that it is one periodic. This shows that $\big (\frac{1}{4}\big )_* v$ is doubly symmetric with respect to $\rho _1$.

It remains to check that if $\big (\frac{1}{4}\big )_* v \in \mathcal {P}^{I_2}_H$ is doubly symmetric with respect to $\rho _1$, it follows that $v \in \mathcal {P}^{I_1}_H$ is doubly symmetry with respect to $\rho _2$. Interchanging in the previous discussion the roles of $\rho _1$ and $\rho _2$, we obtain that

$$\begin{aligned}\big (\tfrac{1}{4}\big )_*\big (\tfrac{1}{4}\big )_*v=\big (\tfrac{1}{2}\big )_*v \in \mathcal {P}^{I_1}_H\end{aligned}$$

is doubly symmetric with respect to $\rho _2$. The fact that $\big (\tfrac{1}{2}\big )_*v$ is invariant under $I_1$ implies that

$$\begin{aligned} I_1 v(t)= & {} \rho _1 \circ v^-(t)\\= & {} \rho _1 \circ v(-t)\\= & {} \rho _1 \circ \Big (\big (\tfrac{1}{2}\big )_* v\Big )\big (-t-\tfrac{1}{2}\big )\\= & {} \rho _1 \circ \Big (\big (\tfrac{1}{2}\big )_* v\Big )^-\big (t+\tfrac{1}{2}\big )\\= & {} I_1\Big (\big (\tfrac{1}{2}\big )_* v\Big )\big (t+\tfrac{1}{2}\big )\\= & {} \Big (\big (\tfrac{1}{2}\big )_*v\Big )\big (t+\tfrac{1}{2}\big )\\= & {} v\big (t+1)\\= & {} v(t), \end{aligned}$$

so that $v \in \mathcal {P}^{I_1}_H$ is as well invariant under $I_1$. Since $\big (\tfrac{1}{2}\big )_*v$ is doubly symmetric with respect to $\rho _2$, we obtain further that

$$\begin{aligned} \rho _2 \circ v(0)= & {} \rho _2 \circ \Big (\big (\tfrac{1}{2}\big )_* v\Big )\big (-\tfrac{1}{2}\big )\\= & {} \rho _2 \circ \Big (\big (\tfrac{1}{2}\big )_* v\Big )\big (\tfrac{1}{2}\big )\\= & {} \rho _2^2 \circ \Big (\big (\tfrac{1}{2}\big )_* v\Big )\big (0\big )\\= & {} \Big (\big (\tfrac{1}{2}\big )_* v\Big )\big (0\big )\\= & {} v\big (\tfrac{1}{2}\big ), \end{aligned}$$

so that v is doubly symmetric with respect to $\rho _2$ as well. This finishes the proof of the lemma. $\square$

5 The reduced monodromy

Suppose that $(M,\omega )$ is a symplectic manifold and $H :M \rightarrow \mathbb {R}$ is a smooth function. We denote by $\phi ^t_H$ the flow of the Hamiltonian vector field of H, characterized by

$$\begin{aligned}\phi ^0_H(x)=x,\quad \frac{d}{dt}\phi ^t_H(x)=X_H(\phi ^t_H(x)), \qquad x \in M.\end{aligned}$$

If v is a simple periodic orbit of $X_H$ of period $\tau$, we have

$$\begin{aligned}\phi ^\tau _H(v(0))=v(0),\end{aligned}$$

i.e., v(0) is a fixed point of $\phi ^\tau _H$. The differential of the flow

$$\begin{aligned}d\phi ^\tau _H(v(0)) :T_{v(0)} M \rightarrow T_{v(0)} M\end{aligned}$$

is a linear symplectic map of the symplectic vector space $(T_{v(0)}M,\omega _{v(0)})$ into itself. This map is referred to as the unreduced monodromy. Since H is autonomous, i.e., does not depend on time, we have

$$\begin{aligned}d\phi ^\tau _H(v(0))X_H(v(0))=X_H(v(0)).\end{aligned}$$

Moreover, by preservation of energy the Hamiltonian H is preserved along the flow of its Hamiltonian vector field. In particular, if c is the energy of v, i.e., the value H attains along v, the differential of the flow maps the tangent space $T_{v(0)}\Sigma$ of the energy hypersurface

$$\begin{aligned}\Sigma =H^{-1}(c)\end{aligned}$$

back to itself. Therefore, the unreduced monodromy induces a linear map

$$\begin{aligned}M_v:=\overline{d \phi ^\tau _H(v(0))} :T_{v(0)}\Sigma /\langle X_H(v(0))\rangle \rightarrow T_{v(0)}\Sigma /\langle X_H(v(0))\rangle \end{aligned}$$

which is still symplectic for the symplectic structure on $T_{v(0)}\Sigma /\langle X_H(v(0))\rangle$ induced from $\omega _{v(0)}$. This map is referred to as the reduced monodromy. Instead of restricting our attention to 0, we could consider the reduced monodromy

$$\begin{aligned}M_v^t:=\overline{d \phi ^\tau _H(v(t))} :T_{v(t)}\Sigma /\langle X_H(v(t))\rangle \rightarrow T_{v(t)}\Sigma /\langle X_H(v(t))\rangle \end{aligned}$$

for any $t \in S^1$. Note that for different times t the reduced monodromies are symplectically conjugated to each other by the flow.

Suppose now in addition that $\rho$ is a real structure on $(M,\omega )$ under which H is invariant and $v \in \mathcal {P}_H^I$ is a symmetric periodic orbit. Since both points v(0) and $v\big (\tfrac{1}{2}\big )$ lie in the fixed point set of $\rho$, the differential of $\rho$ gives rise to linear antisymplectic involutions

$$\begin{aligned}d\rho \big (v\big (0\big )\big ) :T_{v(0)} M \rightarrow T_{v(0)} M, \quad d\rho \big (v\big (\tfrac{1}{2}\big )\big ) :T_{v(1/2)} M \rightarrow T_{v(1/2)} M \end{aligned}$$

which induce real structures on the quotient spaces $T_{v(0)}\Sigma /\langle X_H(v(0))\rangle$, respectively, $T_{v(1/2)}\Sigma /\langle X_H(v(1/2))\rangle$. Since the Hamiltonian vector field is anti-invariant, the antisymplectic involution $\rho$ conjugates the forward flow to the backward flow

$$\begin{aligned}\rho \phi ^t_H \rho =\phi ^{-t}_H.\end{aligned}$$

In particular, differentiating this identity we have

$$\begin{aligned}d\rho \big (v\big (\tfrac{1}{2}\big )\big ) \circ d\phi ^{\tau /2}_H\big (v\big (0\big )\big ) \circ d\rho \big (v\big (0\big )\big )=\Big (d \phi _H^{\tau /2}\big (v\big (\tfrac{1}{2}\big ) \big )\Big )^{-1}.\end{aligned}$$

Therefore, the induced maps

$$\begin{aligned}\Psi :=\overline{d\phi ^{\tau /2}_H\big (v\big (0\big )\big )} :T_{v(0)}\Sigma /\langle X_H(v(0))\rangle \rightarrow T_{v(1/2)}\Sigma /\langle X_H(v(1/2))\rangle \end{aligned}$$

and

$$\begin{aligned}\Phi :=\overline{d\phi ^{\tau /2}_H\big (v\big (\tfrac{1}{2}\big )\big )} :T_{v(1/2)}\Sigma /\langle X_H(v(1/2))\rangle \rightarrow T_{v(0)}\Sigma /\langle X_H(v(0))\rangle \end{aligned}$$

give rise to a real couple $(\Psi ,\Phi )$. Note that the compositions coincide with the reduced monodromies at times 0 and $\tfrac{1}{2}$

$$\begin{aligned}\Phi \Psi =\overline{d\phi ^{\tau }_H\big (v\big (0\big )\big )}, \quad \Psi \Phi =\overline{d\phi ^{\tau }_H\big (v\big (\tfrac{1}{2}\big )\big )}.\end{aligned}$$

Now, we even assume that the symplectic manifold $(M,\omega )$ is doubly real with real structures $\rho _1$ and $\rho _2$ under both of which H is invariant and $v \in \mathcal {P}^{I_1}_H$ is doubly symmetric with respect to $\rho _2$. The differential of $\rho _2$ gives rise to a linear antisymplectic map

$$\begin{aligned}d\rho _2(v(0)) :T_{v(0)}M \rightarrow T_{v(1/2)}M\end{aligned}$$

which induces an antisymplectic map on the quotient spaces

$$\begin{aligned}S :T_{v(0)}\Sigma /\langle X_H(v(0))\rangle \rightarrow T_{v(1/2)}\Sigma /\langle X_H(v(1/2))\rangle .\end{aligned}$$

Since $\rho _1$ commutes with $\rho _2$ this map interchanges the real structures. By Lemma 4.2, we have that $\big (\tfrac{1}{4}\big )_*v \in \mathcal {P}^{I_2}_H$ and therefore S makes the real couple $(\Psi ,\Phi )$ symmetric. Therefore, we obtain, as a consequence of Corollary 3.4, the following corollary, which is Theorem A from Introduction:

Corollary 5.1

A doubly symmetric periodic orbit on a four-dimensional symplectic manifold cannot be negative hyperbolic.