Abstract
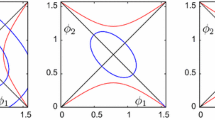
We consider the two-body problem on surfaces of constant nonzero curvature and classify the relative equilibria and their stability. On the hyperbolic plane, for each \(q>0\) we show there are two relative equilibria where the masses are separated by a distance q. One of these is geometrically of elliptic type and the other of hyperbolic type. The hyperbolic ones are always unstable, while the elliptic ones are stable when sufficiently close, but unstable when far apart. On the sphere of positive curvature, if the masses are different, there is a unique relative equilibrium (RE) for every angular separation except \(\pi /2\). When the angle is acute, the RE is elliptic, and when it is obtuse the RE can be either elliptic or linearly unstable. We show using a KAM argument that the acute ones are almost always nonlinearly stable. If the masses are equal, there are two families of relative equilibria: one where the masses are at equal angles with the axis of rotation (‘isosceles RE’) and the other when the two masses subtend a right angle at the centre of the sphere. The isosceles RE are elliptic if the angle subtended by the particles is acute and is unstable if it is obtuse. At \(\pi /2\), the two families meet and a pitchfork bifurcation takes place. Right-angled RE are elliptic away from the bifurcation point. In each of the two geometric settings, we use a global reduction to eliminate the group of symmetries and analyse the resulting reduced equations which live on a five-dimensional phase space and possess one Casimir function.











Similar content being viewed by others
Notes
We mention only the paper (Bolsinov et al. 2012) on the Conley index where new isosceles vortex configurations were found and their stability was established using topological methods.
This assumption is done without loss of generality since one may eliminate these quantities from the equations of motion (2.8) by rescaling time \(t\rightarrow \frac{\sqrt{\varkappa } t}{\mu _1}\), and the momenta \(p\rightarrow \frac{p}{\sqrt{\varkappa }} , \; {\varvec{m}}\rightarrow \frac{ \varvec{m}}{\sqrt{\varkappa }}\), where \(\varkappa =\mu _1\sqrt{G\mu _2}\).
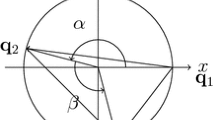
In fact \((\alpha ,q,z,p)\) as defined are Darboux coordinates that generalize the Andoyer variables on \(T^*SO(3)\).
As before, \((\alpha ,q,z,p)\) are Darboux coordinates that generalize the Andoyer variables on \(T^*SO(3)\).
An alternative proof is given in (2018) by working on a symplectic slice of the unreduced system.
References
Bolsinov, A.V., Borisov, A.V., Mamaev, I.S.: Topology and stability of integrable systems. Russ. Math. Surv. 65(2), 259–318 (2010)
Bolsinov, A.V., Borisov, A.V., Mamaev, I.S.: The bifurcation analysis and the Conley Index in mechanics. Regul. Chaotic Dyn. 17(5), 457–478 (2012)
Borisov A.V., Mamaev I.S., Rigid body dynamics. Hamiltonian methods, integrability, chaos. Institute of Computer Science, Moscow–Izhevsk (in Russian) (2005)
Borisov, A.V., Mamaev, I.S.: Reduction in the two-body problem on the Lobatchevsky plane. Russ. J. Nonlinear Dyn. 2(3), 279–285 (2006). (in Russian)
Borisov, A.V., Mamaev, I.S.: Rigid body dynamics in NonEuclidean spaces. Russ. J. Math. Phys. 23(4), 431–453 (2016)
Borisov, A.V., Mamaev, I.S.: The restricted two-body problem in constant curvature spaces. Celest. Mech. Dyn. Astron. 96(1), 1–17 (2006)
Borisov, A.V., Mamaev, I.S., Bizyaev, I.A.: The spatial problem of 2 bodies on a sphere. Reduction and stochasticity. Regul. Chaotic Dyn. 21(5), 556–580 (2016)
Borisov, A.V., Mamaev, I.S., Kilin, A.A.: Two-body problem on a sphere: reduction, stochasticity. Period. Orbits. Regul. Chaotic Dyn. 9(3), 265–279 (2004)
Cariñena, J.F., Rañada, M.F., Santander, M.: Central potentials on spaces of constant curvature: the Kepler problem on the two dimensional sphere \(S^2\) and the hyperbolic plane \(H^2\). J. Math. Phys. 46, 052702 (2005)
Chernoivan, V.A., Mamaev, I.S.: The restricted two-body problem and the Kepler problem in the constant curvature spaces. Regul. Chaotic Dyn. 4(2), 112–124 (1999)
Diacu, F.: Relative Equilibria of the Curved \(N\)-Body Problem. Atlantis, Paris (2012)
Diacu, F., Pérez-Chavela, E., Reyes, J.G.: An intrinsic approach in the curved n-body problem. The negative case. J. Differ. Equ. 252, 4529–4562 (2012)
García-Naranjo, L.C., Marrero, J.C., Pérez-Chavela, E., Rodríguez-Olmos, M.: Classification and stability of relative equilibria for the two-body problem in the hyperbolic space of dimension 2. J. Differ. Equ. 260, 6375–6404 (2016)
Iversen, B.: Hyperbolic Geometry, vol. 25. LMS Student Texts, London (1992)
Kilin, A.A.: Libration Points in Spaces \(S^2\) and \(L^2\). Regul. Chaotic Dyn. 4(1), 91–103 (1999)
Killing, H.W.: Die Mechanik in den nicht-euklidischen Raumformen. J. Reine Angew. Math. 98(1), 1–48 (1885)
Kozlov, V.V., Harin, A.O.: Kepler’s problem in constant curvature spaces. Cel. Mech. Dyn. Astron. 54, 393–399 (1992)
Markeev, A.P.: Libration points in celestial mechanics and cosmodynamics. M. Nauka (1978) (in Russian)
Marsden, J.E.: Lectures on Mechanics. C.U.P. (1992)
Meyer, K.R., Hall, G.R., Offin, D.: Introduction to Hamiltonian dynamical systems and the \(N\)-body problem. Second edition. Applied Mathematical Sciences, 90. Springer, New York, (2009)
Montaldi, J.: Relative equilibria and conserved quantities in symmetric Hamiltonian systems. In: Peyresq Lectures in Nonlinear Phenomena, World Scientific (2000)
Montaldi, J., Nava-Gaxiola, C.: Point vortices on the hyperbolic plane. J. Math. Phys. 55, 102702 (2014)
Montanelli, H.: Computing hyperbolic choreographies. Regul. Chaotic Dyn. 21(5), 523–531 (2016)
Moser, J.: Lectures on Hamiltonian Systems, vol. 81. American Mathematical Soc, Providence (1968)
Pérez-Chavela, E., Reyes-Victoria, J.G.: An intrinsic approach in the curved n-body problem. The positive curvature case. Trans. Am. Math. Soc. 364, 3805–3827 (2012)
Rodríguez-Olmos, M.: Relative equilibria for the two-body problem on \(S^2\). In preparation (2018)
Schering, E.: Die Schwerkraft in mehrfach ausgedehnten Gaussischen und Riemannschen Räumen. Nachr. Koönigl. Ges. Wiss. Göttingen 1873, 149–159 (1873)
Serret, P.J.: Théorie nouvelle géométrique et mécanique des lignes a double courbure. Librave de Mallet-Bachelier, Paris (1860)
Shchepetilov, A.V.: Two-body problem on spaces of constant curvature: 1. Dependence of the Hamiltonian on the Symmetry Group and the reduction of the classical system. Theor. Math. Phys. 124(2), 1068–1081 (2000)
Shchepetilov, A.V.: Calculus and Mechanics on Two-Point Homogenous Riemannian Spaces. Lect. Notes Phys., vol. 707. Springer, Berlin (2006)
Siegel, C.L., Moser, J.K.: Lectures on Celestial Mechanics. Translated from the German by C. I. Kalme. Reprint of the 1971 Translation. Classics in Mathematics, p. 1995. Springer, Berlin (1995)
Acknowledgements
We are thankful to both reviewers and the associate editor for their remarks and criticisms which led to an improvement of our paper. We are grateful to Miguel Rodríguez-Olmos for discussing his preliminary results of (2018) with us. The authors express their gratitude to B. S. Bardin and I. A. Bizyaev for fruitful discussions and useful comments. The research contribution of LGN and JM was made possible by a Newton Advanced Fellowship from the Royal Society, Ref: NA140017. The work of AVB and ISM is supported by the Russian Foundation for Basic Research (Project No. 17-01-00846-a). The research of AVB was also carried out within the framework of the state assignment of the Ministry of Education and Science of Russia.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Borisov, A.V., García-Naranjo, L.C., Mamaev, I.S. et al. Reduction and relative equilibria for the two-body problem on spaces of constant curvature. Celest Mech Dyn Astr 130, 43 (2018). https://doi.org/10.1007/s10569-018-9835-7
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10569-018-9835-7