Skip to main content
SpringerLink
Log in

Orbit uncertainty propagation and sensitivity analysis with separated representations

  • Original Article
  • Published:
Celestial Mechanics and Dynamical Astronomy Aims and scope Submit manuscript

Abstract

Most approximations for stochastic differential equations with high-dimensional, non-Gaussian inputs suffer from a rapid (e.g., exponential) increase of computational cost, an issue known as the curse of dimensionality. In astrodynamics, this results in reduced accuracy when propagating an orbit-state probability density function. This paper considers the application of separated representations for orbit uncertainty propagation, where future states are expanded into a sum of products of univariate functions of initial states and other uncertain parameters. An accurate generation of separated representation requires a number of state samples that is linear in the dimension of input uncertainties. The computation cost of a separated representation scales linearly with respect to the sample count, thereby improving tractability when compared to methods that suffer from the curse of dimensionality. In addition to detailed discussions on their construction and use in sensitivity analysis, this paper presents results for three test cases of an Earth orbiting satellite. The first two cases demonstrate that approximation via separated representations produces a tractable solution for propagating the Cartesian orbit-state uncertainty with up to 20 uncertain inputs. The third case, which instead uses Equinoctial elements, reexamines a scenario presented in the literature and employs the proposed method for sensitivity analysis to more thoroughly characterize the relative effects of uncertain inputs on the propagated state.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18

Similar content being viewed by others

References

  • Ammar, A., Chinesta, F., Joyot, P.: The nanometric and micrometric scales of the structure and mechanics of materials revisited: an introduction to the challenges of fully deterministic numerical descriptions. Int. J. Multiscale Comput. Eng. 6(3), 191–213 (2008). doi:10.1615/IntJMultCompEng.v6.i3.20

    Article  Google Scholar 

  • Askey, R.A., Arthur, W.J.: Some basic Hypergeometric Orthogonal Polynomials that Generalize Jacobi Polynomials, vol. 319. AMS, Providence (1985)

    MATH  Google Scholar 

  • Balducci, M., Jones, B.A., Doostan, A.: Orbit uncertainty propagation with separated representations. AAS/AIAA Astrodynamics Specialist Conference Hilton Head, SC, August 11–15 (2013)

  • Beylkin, G., Mohlenkamp, M.J.: Algorithms for numerical analysis in high dimensions. SIAM J. Sci. Comput. 26(6), 2133–2159 (2005). doi:10.1137/040604959

    Article  MathSciNet  MATH  Google Scholar 

  • Beylkin, G., Garcke, J., Mohlenkamp, M.J.: Multivariate regression and machine learning with sums of separable functions. SIAM J. Sci. Comput. 31(3), 1840–1857 (2009). doi:10.1137/070710524

    Article  MathSciNet  MATH  Google Scholar 

  • Blatman, G., Sudret, B.: Efficient computation of global sensitivity indices using sparse polynomial chaos expansions. Reliab. Eng. Syst. Saf. 95, 1216–1229 (2010). doi:10.1016/j.ress.2010.06.015

    Article  Google Scholar 

  • Chevreuil, M., Lebrun, R., Nouy, A., Rai, P.: A least-squares method for sparse low rank approximation of multivariate functions. arXiv preprint arXiv:1305.0030 (2013)

  • Chinesta, F., Ladeveze, P., Cueto, E.: A short review on model order reduction based on proper generalized decomposition. Arch. Comput. Methods Eng. 18(4), 395–404 (2011)

    Article  Google Scholar 

  • Cohen, A., DeVore, R., Schwab, C.: Convergence rates of best n-term Galerkin approximations for a class of elliptic spdes. Found. Comput. Math. 10(6), 615–646 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  • DeMars, K.J., Bishop, R.H., Jah, M.K.: Entropy-based approach for uncertainty propagation of nonlinear dynamical systems. J. Guid. Control Dyn. 36(4), 1047–1057 (2013). doi:10.2514/1.58987

    Article  ADS  Google Scholar 

  • DeMars, K.J., Cheng, Y., Jah, M.K.: Making best use of model evaluations to compute sensitivity indices. J. Guid. Control Dyn. 37(3), 979–984 (2014). doi:10.2514/1.62308

    Article  ADS  Google Scholar 

  • Doostan, A., Iaccarino, G., Etemadi, N.: A least-squares approximation of high-dimensional uncertain systems. Technical Report, Annual Research Brief, Center for Turbulence Research, Stanford University (2007)

  • Doostan, A., Iaccarino, G.: A least-squares approximation of partial differential equations with high-dimensional random inputs. J. Comput. Phys. 228(12), 4332–4345 (2009)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Doostan, A., Validi, A., Iaccarino, G.: Non-intrusive low-rank separated approximation of high-dimensional stochastic models. Comput. Methods Appl. Mech. Eng. 263, 42–55 (2013). doi:10.1016/j.cma.2013.04.003

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Fann, G., Beylkin, G., Harrison, R., Jordan, K.: Singular operators in multiwavelet bases. IBM J. Res. Dev. 48(2), 161–171 (2004). doi:10.1147/rd.482.0161

    Article  Google Scholar 

  • Forrester, A., Sobester, A., Keane, A.: Engineering design via surrogate modelling: a practical guide. Wiley, Hoboken (2008)

    Book  Google Scholar 

  • Friedman, J., Hastie, T., Tibshirani, R.: The Elements of Statistical Learning, vol. 1. Springer, Berlin (2001)

    MATH  Google Scholar 

  • Fujimoto, K., Scheeres, D.J., Alfriend, K.T.: Analytical nonlinear propagation of uncertainty in the two-body problem. J. Guid. Control Dyn. 35(2), 497–509 (2012). doi:10.2514/1.54385

    Article  ADS  Google Scholar 

  • Ghanem, R., Spanos, P.: Stochastic Finite Elements: A Spectral Approach. Springer, New York (1991)

    Book  MATH  Google Scholar 

  • Hadigol, M., Doostan, A., Matthies, H.G., Niekamp, R.: Partitioned treatment of uncertainty in coupled domain problems: a separated representation approach. Comput. Methods Appl. Mech. Eng. 274, 103–124 (2014). doi:10.1016/j.cma.2014.02.004

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Hampton, J., Doostan, A.: Coherence motivated sampling and convergence analysis of least squares polynomial chaos regression. Comput. Methods Appl. Mech. Eng. 290, 73–97 (2015). doi:10.1016/j.cma.2015.02.006

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Hansen, M., Schwab, C.: Analytic regularity and nonlinear approximation of a class of parametric semilinear elliptic PDEs. Math. Nachr. 286, 832–860 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  • Harrison, R.J., Fann, G.I., Yanai, T., Gan, Z., Beylkin, G.: Multiresolution quantum chemistry: basic theory and initial applications. J. Chem. Phys. 121(23), 11587–11598 (2004). doi:10.1063/1.1791051

    Article  ADS  Google Scholar 

  • Hoang, V.H., Schwab, C.: Sparse tensor Galerkin discretization of parametric and random parabolic PDEs—analytic regularity and generalized polynomial chaos approximation. SIAM J. Math. Anal. 45(5), 3050–3083 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  • Horwood, J.T., Aragon, N.D., Poore, A.B.: Gaussian sum filters for space surveillance: theory and simulations. J. Guid. Control Dyn. 34(6), 1839–1851 (2011). doi:10.2514/1.53793

    Article  ADS  Google Scholar 

  • Jones, B.A., Doostan, A.: Satellite collision probability estimation using polynomial chaos expansions. Adv. Space Res. 52(11), 1860–1875 (2013). doi:10.1016/j.asr.2013.08.027

    Article  ADS  Google Scholar 

  • Jones, B.A., Doostan, A., Born, G.: Nonlinear propagation of orbit uncertainty using non-intrusive polynomial chaos. J. Guid. Control Dyn. 36(2), 430–444 (2013). doi:10.2514/1.57599

  • Jones, B.A., Parrish, N., Doostan, A.: Post-maneuver collision probability estimation using sparse polynomial chaos expansions. J. Guid. Control Dyn. 38(8), 1425–1437 (2015). doi:10.2514/1.G000595

  • Junkins, J.L., Akella, M.R., Alfriend, K.T.: Non-gaussian error propagation in orbital mechanics. J. Astronaut. Sci. 44(4), 541–563 (1996)

    Google Scholar 

  • Khoromskij, B.N., Schwab, C.: Tensor-structured Galerkin approximation of parametric and stochastic elliptic pdes. SIAM J. Sci. Comput. 33, 364–385 (2010). doi:10.1137/100785715

    Article  MathSciNet  MATH  Google Scholar 

  • Kolda, T.G., Bader, B.W.: Tensor decompositions and applications. SIAM Rev. 51(3), 455–500 (2009)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Majji, M., Junkins, J., Turner, J.: A high order method for estimation of dynamic systems. J. Astronaut. Sci. 56(3), 401–440 (2008). doi:10.1007/BF03256560

    Article  ADS  Google Scholar 

  • Nielsen, P., Alfriend, K., Bloomfield, M., Emmert, J., Miller, J., Guo, Y., et al.: Continuing Kepler’s Quest: Assessing Air Force Space Command’s Astrodynamic Standards. The National Academies Press, Washington (2012)

    Google Scholar 

  • Nouy, A.: Proper generalized decompositions and separated representations for the numerical solution of high dimensional stochastic problems. Arch. Comput. Methods Eng. 17, 403–434 (2010). doi:10.1007/s11831-010-9054-1

    Article  MathSciNet  MATH  Google Scholar 

  • Park, R.S., Scheeres, D.J.: Nonlinear mapping of gaussian statistics: theory and applications to spacecraft trajectory design. J. Guid. Control Dyn. 29(6), 1367–1375 (2006). doi:10.2514/1.20177

    Article  ADS  Google Scholar 

  • Quadrelli, M.B., Wood, L.J., Riedel, J.E., McHenry, M.C., Aung, M., Cangahuala, L.A., et al.: Guidance, navigation, and control technology assessment for future planetary science missions. J. Guid. Control Dyn. 38(7), 1165–1186 (2015). doi:10.2514/1.G000525

    Article  ADS  Google Scholar 

  • Reynolds, M., Doostan, A., Beylkin, G.: Randomized alternating least squares for canonical tensor decompositions: application to a PDE with random data. arXiv preprint arXiv:1510.01398 (2015)

  • Russell, R.: Survey of spacecraft trajectory design in strongly perturbed environments. J. Guid. Control Dyn. 35(3), 705–720 (2012). doi:10.2514/1.56813

    Article  ADS  Google Scholar 

  • Sabol, C., Binz, C., Segerman, A., Roe, K., Schumacher Jr., P.W.: Probability of collision with special perturbations dynamics using the Monte Carlo method. In: AAS/AIAA Astrodynamics Specialist Conference, Girdwood, AK (2011)

  • Saltelli, A.: Making best use of model evaluations to compute sensitivity indices. Comput. Phys. Commun. 145, 280–297 (2002). doi:10.1016/S0010-4655(02)00280-1

    Article  ADS  MATH  Google Scholar 

  • Saltelli, A., Tarantola, S., Campolongo, F., Ratto, M.: Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models. Wiley, Hoboken (2004)

    MATH  Google Scholar 

  • Schutz, B., Tapley, B., Born, G.H.: Statistical Orbit Determination. Academic Press, Cambridge (2004)

    Google Scholar 

  • Smith, R.: Uncertainty quantification: theory, implementation, and applications. SIAM Soc. Ind. Appl. Math. 12, 323–331 (2013)

  • Sobol, I.: Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 55, 271–280 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  • Sun, Y., Kumar, M.: Uncertainty propagation in orbital mechanics via tensor decomposition. Celest. Mech. Dyn. Astrono. 124(3), 269–294 (2015). doi:10.1007/s10569-015-9662-z

  • Tamellini, L., Le Maitre, O., Nouy, A.: Model reduction based on proper generalized decomposition for the stochastic steady incompressible Navier-Stokes equations. SIAM J. Sci. Comput. 36(3), A1089–A1117 (2014). doi:10.1137/120878999

    Article  MathSciNet  MATH  Google Scholar 

  • Tapley, B., Ries, J., Bettadpur, S., Chambers, D., Cheng, M., Condi, et al.: Ggm02 - an improved earth gravity field model from GRACE. J. Geod. (2005). doi:10.1007/s00190-005-0480-z

  • Vallado, D.: Fundamentals of Astrodynamics and Applications, 3rd edn, chapter 8.6. Microcosm Press, Hawthorne, CA, p 562 (2007)

  • Xiu, D.: Numerical Methods for Stochastic Computations: a Spectral Method Approach. Princeton University Press, Princeton (2010)

    MATH  Google Scholar 

Download references

Acknowledgements

The material for the work by Marc Balducci is provided by the NSTRF fellowship, NASA Grant NNX15AP41H. This material is based upon work of Alireza Doostan supported by the US Department of Energy Office of Science, Office of Advanced Scientific Computing Research, under Award Number DE-SC0006402 and NSF Grants DMS-1228359 and CMMI-1454601.

Author information

Authors and Affiliations

  1. Colorado Center for Astrodynamics Research, University of Colorado Boulder, Boulder, CO, 80309, USA

    Marc Balducci & Brandon Jones

  2. Aerospace Engineering, University of Colorado Boulder, Boulder, CO, 80309, USA

    Alireza Doostan

Authors
  1. Marc Balducci
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Brandon Jones
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Alireza Doostan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Marc Balducci.

Appendix

Appendix

See Table 15.

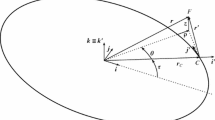
Table 15 Low degree Stokes coefficients
Full size table

Note that \(f_r\) is a retrograde factor, where it is +1 for all direct orbits and \(-1\) for nearly retrograde orbits (Vallado 2007).

$$\begin{aligned} h_e= & {} e \sin {\omega + f_r \varOmega }. \end{aligned}$$
(37)
$$\begin{aligned} k_e= & {} e \cos {\omega + f_r \varOmega }.\end{aligned}$$
(38)
$$\begin{aligned} p_e= & {} \frac{\sin {i}\sin {\varOmega }}{1 + \cos ^{f_r}{i}}. \end{aligned}$$
(39)
$$\begin{aligned} q_e= & {} \frac{\sin {i}\cos {\varOmega }}{1 + \cos ^{f_r}{i}}. \end{aligned}$$
(40)
$$\begin{aligned} \lambda _{{\mathcal {M}}}= & {} {\mathcal {M}} + \omega + f_r \varOmega . \end{aligned}$$
(41)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Balducci, M., Jones, B. & Doostan, A. Orbit uncertainty propagation and sensitivity analysis with separated representations. Celest Mech Dyn Astr 129, 105–136 (2017). https://doi.org/10.1007/s10569-017-9767-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10569-017-9767-7

Keywords

Search

Navigation