Relative equilibria of the restricted three-body problem in curved spaces

Abstract

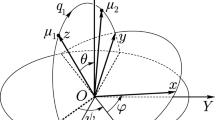
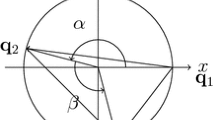
We use a formulation of the N-body problem in spaces of constant Gaussian curvature, ${\kappa }\in \mathbb {R}$, as widely used by A. Borisov, F. Diacu and their coworkers. We consider the restricted three-body problem in $\mathbb {S}^2$ with arbitrary ${\kappa }>0$ (resp. $\mathbb {H}^2$ with arbitrary ${\kappa }<0$) in a formulation also valid for the case ${\kappa }=0$. For concreteness when ${\kappa }>0$ we restrict the study to the case of the three bodies at the upper hemisphere, to be denoted as $\mathbb {S}^2_+$. The main goal is to obtain the totality of relative equilibria as depending on the parameters ${\kappa }$ and the mass ratio $\mu$. Several general results concerning relative equilibria and its stability properties are proved analytically. The study is completed numerically using continuation from the ${\kappa }=0$ case and from other limit cases. In particular both bifurcations and spectral stability are also studied. The $\mathbb {H}^2$ case is similar, in some sense, to the planar one, but in the $\mathbb {S}^2_+$ case many differences have been found. Some surprising phenomena, like the coexistence of many triangular-like solutions for some values $({\kappa },\mu )$ and many stability changes will be discussed.

Appendix

In this Appendix we give reduced formulas for the functions which appear in the equations of the restricted problem.

Let us consider the functions $\rho _{ij}, f_{ij}, g_{ij}$ defined in (5). It is easy to check that they can be written as

$$\begin{aligned}&{\kappa }\rho _{ij}^2 = 2 [1- {\kappa }(\xi _i \xi _j + \eta _i \eta _j) - E_i E_j], \nonumber \\&f_{ij} = {\kappa }(\xi _i \xi _j + \eta _i \eta _j) + E_i E_j, \qquad 1- f_{ij}^2 = {\kappa }\Delta _{ij}, \end{aligned}$$

(50)

$$\begin{aligned}&\Delta _{ij} \!= \!\xi _i^2 \!+\! \eta _i^2 \!+ \!\xi _j^2\! +\! \eta _j^2\! -\! {\kappa }( \xi _i^2\! +\! \eta _i^2)(\xi _j^2 \!+\! \eta _j^2)- {\kappa }(\xi _i\xi _j\!+\!\eta _i\eta _j)^2-2(\xi _i\xi _j+\eta _i\eta _j ) E_i E_j, \nonumber \\ \end{aligned}$$

(51)

$$\begin{aligned}&g_{ij}:= \frac{1}{d_{ij}^3} = \left( \frac{{\kappa }}{1-f_{ij}^2} \right) ^{3/2} = \frac{1}{\Delta _{ij}^{3/2}}, \end{aligned}$$

(52)

where $E_i=\sqrt{1- {\kappa }(\xi _i^2 + \eta _i^2)}.$

If $\mathbf{U}_1=(\xi _1,\eta _1)^T=(r_1,0)^T,$ $\mathbf{U}_2=(\xi _2,\eta _2)^T=(-r_2,0)^T,$ $\mathbf{U}_3= (\xi _3,\eta _3)^T = (x,y)^T,$ then

$$\begin{aligned}&{\kappa }\rho _{13}^2 = 2 (1 - {\kappa }r_1 x - E_1 E_3), \quad {\kappa }\rho _{23}^2 = 2 (1 + {\kappa }r_2 x - E_2 E_3), \end{aligned}$$

(53)

$$\begin{aligned}&f_{13} = {\kappa }r_1 x + E_1 E_3, \quad f_{23} = - {\kappa }r_2 x + E_2 E_3, \end{aligned}$$

(54)

$$\begin{aligned}&g_{13} = \Delta _{13}^{-3/2}, \quad g_{23} = \Delta _{23}^{-3/2}, \quad \Delta _{13}= y^2 + S_1^2, \quad \Delta _{23} = y^2 + S_2^2, \end{aligned}$$

(55)

$$\begin{aligned}&S_1 = x E_1 - r_1 E_3, \quad S_2 = x E_2 + r_2 E_3, \end{aligned}$$

(56)

where $E_j= \sqrt{1-{\kappa }r_j^2},$ $j=1,2$, $E_3 = \sqrt{1-{\kappa }(x^2 + y^2)}$. Then one has

$$\begin{aligned} f_{13} x - r_1 = - {\kappa }r_1 y^2+ S_1 E_3, \qquad f_{23} x + r_2 = {\kappa }r_2 y^2 + S_2 E_3 \end{aligned}$$

(57)

and, furthermore

$$\begin{aligned} \frac{\partial f_{13}}{\partial x } = - \frac{{\kappa }S_1}{E_3}, \qquad \frac{\partial f_{23}}{\partial x } = - \frac{{\kappa }S_2}{E_3}, \qquad \frac{\partial S_1}{\partial x } = \frac{f_{13}}{E_3}, \qquad \frac{\partial S_2}{\partial x } = \frac{f_{23}}{E_3}. \end{aligned}$$

(58)

Lemma 7.1

Assume ${\kappa }>0$ and $r_1,r_2$ fixed. Then $f_{13}$ and $f_{23}$ are convex functions in $C_{{\kappa }}:=\{ (x,y)\in \mathbb {R}^2 \,|\,{\kappa }(x^2+y^2) < 1 \}$, such that for any $(x,y) \in C_{{\kappa }}$

$$\begin{aligned} - \sqrt{{\kappa }} r_1< f_{13} \le 1, \qquad - \sqrt{{\kappa }} r_2 < f_{23} \le 1.\end{aligned}$$

Moreover $f_{13}=0$ along the curve $\gamma _{13} = \{ (x,y) | x \le 0, {\kappa }(x^2 + E_1^2 y^2 ) = E_1^2 \}$, and $f_{23}=0$ on the curve $\gamma _{23} = \{ (x,y) | x \ge 0, {\kappa }(x^2 + E_2^2 y^2 ) = E_2^2 \}$.

If ${\kappa }<0$, then $f_{13}>0$ and $f_{23}>0$ at any point.

Proof

Using

$$\begin{aligned} \frac{\partial ^2 f_{13}}{\partial x^2} = - \frac{{\kappa }E_1}{E_3^3} (1-{\kappa }y^2)< 0, \quad \frac{\partial ^2 f_{13}}{\partial y \partial x} = - {\kappa }^2 x y \frac{E_1}{E_3^3}, \quad \frac{\partial ^2 f_{13}}{\partial y^2} = - \frac{{\kappa }E_1}{E_3^3} (1-{\kappa }x^2) <0, \end{aligned}$$

it follows that the Hessian of $f_{13}$ is negative definite in $C_{{\kappa }}$. Similar formulas hold for $f_{23}$ by replacing $E_1$ by $E_2$. The maximum for $f_{13}$ is equal to 1 and it is attained at the point $(x,y)=(r_1,0)$ and the minimum is achieved at the point $(x,y)= (-1/\sqrt{{\kappa }},0).$ Similar for $f_{23}$. The case ${\kappa }<0$ is obvious from (3). $\square$

Let us consider the functions ${\hat{F}}$, ${\hat{G}}$ introduced in Sect. 6. We compute the partial derivatives

$$\begin{aligned} {\hat{F}}_x= & {} \frac{1}{E_3} \left\{ - 3 m_1 (r_1 - x f_{13} ) f_{13} S_1 \Delta _{13}^{-5/2} + 3 m_2 (r_2 + x f_{23} ) f_{23} S_2 \Delta _{23}^{-5/2} \right. \nonumber \\&\left. -E_3 [ m_1 f_{13} g_{13} + m_2 f_{23} g_{23} ] + {\kappa }x [ m_1 S_1 g_{13} + m_2 S_2 g_{23} ] \right\} , \nonumber \\ {\hat{F}}_y= & {} \frac{y}{E_3} \left\{ - 3 m_1 (r_1 - x f_{13} ) E_1 f_{13} \Delta _{13}^{-5/2} + 3 m_2 (r_2 + x f_{23} ) E_2 f_{23} \Delta _{23}^{-5/2} \right. \nonumber \\&\left. + {\kappa }x \, [ m_1 E_1 g_{13} + m_2 E_2 g_{23} ] \right\} , \nonumber \\ {\hat{G}}_x= & {} \frac{y}{E_3} \left\{ 3 m_1 S_1 f_{13}^2 \Delta _{13}^{-5/2} + 3 m_2 S_2 f_{23}^2 \Delta _{23}^{-5/2} + {\kappa }\, [m_1 S_1 g_{13} + m_2 S_2 g_{23} \,] \right\} , \nonumber \\ {\hat{G}}_y= & {} -\left[ m_1 f_{13} g_{13} + m_2 f_{23} g_{23} \right] \nonumber \\&+ \frac{y^2}{E_3} \left\{ 3 m_1 f_{13}^2 E_1 \Delta _{13}^{-5/2} + 3 m_2 f_{23}^2 E_2 \Delta _{23}^{-5/2} + {\kappa }\,[ \, m_1 E_1 g_{13} + m_2 E_2 g_{23} \,]\right\} .\nonumber \\ \end{aligned}$$

(59)

Lemma 7.2

For any real ${\kappa }$, the following identity holds

$$\begin{aligned} {\hat{F}}_x+{\hat{G}}_y = \frac{1}{E_3} [m_1 E_1 g_{13} + m_2 E_2 g_{23} ]. \end{aligned}$$

(60)

Proof

From (59) it follows

$$\begin{aligned} {\hat{F}}_x+{\hat{G}}_y= & {} -2 \left[ m_1 f_{13} g_{13} + m_2 f_{23} g_{23} \right] + \frac{{\kappa }x}{E_3} \left[ m_1 S_1 g_{13} + m_2 S_2 g_{23}\right] \\&+ \frac{{\kappa }y^2}{E_3}\left[ \, m_1 E_1 g_{13} + m_2 E_2 g_{23} \,\right] \\&+\frac{3 m_1 f_{13}}{E_3} \Delta _{13}^{-5/2} \left[ (r_1 - x f_{13}) S_1 + y^2 f_{13} E_1 \right] \\&+ \frac{3 m_2 f_{23}}{E_3} \Delta _{23}^{-5/2} \left[ (r_2 + x f_{23}) S_2 + y^2 f_{23} E_2 \right] . \end{aligned}$$

Using (57) and (54)

$$\begin{aligned} (r_1 - x f_{13}) S_1 + y^2 f_{13} E_1 = E_3 (y^2 + S_1^2), \quad (r_2 + x f_{23}) S_2 + y^2 f_{23} E_2 = E_3 (y^2 + S_2^2). \end{aligned}$$

Note that from (55), $\Delta _{13}^{-5/2} (y^2 + S_1^2) = \Delta _{13}^{-3/2}= g_{13}$ and $\Delta _{23}^{-5/2} (y^2 + S_2^2) = g_{23}$. Using (56) to write

$$\begin{aligned} m_1 S_1 g_{13} + m_2 S_2 g_{23} = x \left[ \, m_1 E_1 g_{13} + m_2 E_2 g_{23} \,\right] + E_3 \left[ - m_1 r_1 g_{13} + m_2 r_2 g_{23} \right] , \end{aligned}$$

one can easily obtain (60) after some cancellations. $\square$