Abstract
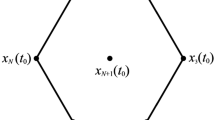
We study the neighborhood of the equal mass regular polygon relative equilibria in the N-body probem, and show that this relative equilibirum is isolated among the co-circular configurations (in which each point lies on a common circle) for which the center of mass is located at the center of the common circle. It is also isolated in the sense that a sufficiently small mass cannot be added to the common circle to form a \(N+1\)-body relative equilibrium. These results provide strong evidence for a conjecture that the equal mass regular polygon is the only co-circular relative equilibrium with its center of mass located at the center of the common circle.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Albouy, A., Cabral, H.E., Santos, A.A.: Some problems on the classical n-body problem. Celest. Mech. Dyn. Astron. 113, 369–375 (2012)
Barutello, V., Terracini, S.: Action minimizing orbits in the n-body problem with simple choreography constraint. Nonlinearity 17, 2015 (2004)
Barutello, V., Ferrario, D.L., Terracini, S.: Symmetry groups of the planar three-body problem and action-minimizing trajectories. Arch. Ration. Mech. Anal. 190, 189–226 (2008)
Checiner, A., Gerver, J., Montgomery, R., Simo, C.: Simple choreographies of \(N\) bodies: a preliminary study. In: Newton, P., Holmes, P., Weinstein, Alan (eds.) Geometry, Mechanics and Dynamics, pp. 287–308. Springer, New York (2002)
Chen, K.-C.: Action-minimizing orbits in the parallelogram four-body problem with equal masses. Arch. Ration. Mech. Anal. 158, 293–318 (2001)
Chenciner, A.: New advances in celestial mechanics and Hamiltonian systems. Are there Perverse Choreographies?. Kluwer/Plenum, New York (2004)
Chenciner, A., Montgomery, R.: A remarkable periodic solution of the three-body problem in the case of equal masses. Ann. Math. 153, 881–902 (2000)
Chenciner, A., Venturelli, A.: Minima de l’intégrale d’action du probléme Newtoniende 4 corps de masses égales dans \(R^3\): orbites ‘hip-hop’. Celest. Mech. Dyn. Astron. 77, 139–151 (2000)
Cors, J.M., Hall, G.R., Roberts, G.E.: Uniqueness results for co-circular central configurations for power-law potentials. Phys. D Nonlinear Phenom. 280, 44–47 (2014)
Ferrario, D.J., Terracini, S.: On the existence of collisionless equivariant minimizers for the classical n-body problem. Invent. Math. 155, 305–362 (2004)
Hampton, M.: Co-circular central configurations in the four-body problem. Equadiff 2003, 993–998 (2003)
Helmholtz, H.: Uber Integrale der hydrodynamischen Gleichungen, Welche den Wirbelbewegungen entsprechen. Crelle’s J. für Math. 55, 25–55 (1858). English translation by P. G. Tait, P.G. On the integrals of the hydrodynamical equations which express vortex-motion, Philosophical Magazine (1867), 485–51
Longley, W.R.: Some particular solutions in the problem of \(n\)-bodies. Bull. Am. Math. Soc. 7, 324–335 (1907)
Maxwell, J.C.: in Maxwell on Saturn’s rings. MIT press, Cambridge (1983)
Moeckel, R.: Linear stability of relative equilibria with a dominant mass. J. Dyn. Diff. Equ. 6, 37–51 (1994)
Newton, I.: Philosophi Naturalis Principia Mathematica. Royal Society, London (1687)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Hampton, M. Splendid isolation: local uniqueness of the centered co-circular relative equilibria in the N-body problem. Celest Mech Dyn Astr 124, 145–153 (2016). https://doi.org/10.1007/s10569-015-9656-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10569-015-9656-x