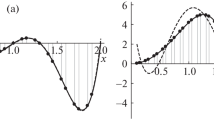
Abstract
An approximation-prediction problem for functions represented by empirical data is analyzed. A class of functions as predictors, the so-called RFT-transformers, based on the least-square and superposition methods is proposed. Special classes of dynamic systems with delay are introduced and analyzed to obtain classical results for calculation of gradients. These results are used to optimize RFT-transformers.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
REFERENCES
A. N. Kolmogorov, “Representation of continuous functions of several variables by superpositions of continuous functions of a smaller number of variables,” Dokl. AN SSSR, 108, No.2, 179–182 (1956).
V. I. Arnol'd, “Functions of three variables,” Dokl. AN SSSR, 114, No.4, 953–956 (1957).
Yu. V. Linnik, The Least-Squares Method and the Fundamentals of Mathematical and Statistical Theory of Processing Observations [in Russian], Fizmatgiz, Moscow (1969).
V. N. Vapnik, Restoration of Functions from Empirical Data [in Russian], Nauka, Moscow (1979).
A. G. Ivakhnenko, Self-Organizing Systems of Recognition and Automatic Control [in Russian], Tekhnika, Kiev (1969).
N. F. Kirichenko, Yu. V. Krack, and A. A. Polishchuk, “Pseudoinverse and projection matrices in problems of synthesis of functional transformers,” Kibern. Sist. Analiz, No. 3, 407–419 (2004).
N. F. Kirichenko, “Analytical representation of perturbations of pseudoinverse matrices,” Kibern. Sist. Analiz, No. 2, 230–238 (1997).
N. F. Kirichenko and N. P. Lepekha, “Perturbation of pseudoinverse and projectional matrices as applied to identification of linear and nonlinear dependences,” Probl. Upravl. Inform., No. 1, 6–22 (2001)
N. F. Kirichenko and N. P. Lepekha, “Application of pseudoinverse and projective matrices to studying control, observation, and identification problems,” Kibern. Sist. Analiz, No. 4, 568–585 (2002).
A. Albert, Regression, Pseudoinversion, Recurrent Estimation [Russian translation], Nauka, Moscow (1977).
A. I. Propoi, Elements of the Theory of Optimal Discrete Processes [in Russian], Nauka, Moscow (1973).
B. N. Bublik and N. F. Kirichenko, Fundamentals of Control Theory [in Russian], Vyssh. Shk., Kiev (1975).
V. M. Kuntsevich and M. M. Lychak, Synthesis of Optimal and Adaptive Control Systems: Game Approach [in Russian], Naukova Dumka, Kiev (1985).
B. N. Bublik, F. G. Garashchenko, and N. F. Kirichenko, Structural and Parametric Optimization and Stability of Dynamic Bundles [in Russian], Naukova Dumka, Kiev (1985).
F. O. Sopronyuk, Simulation and Optimization of Control Systems with Branching Structures [in Russian], Ruta, Chernovtsy (1995).
Yu. Tu, Modern Control Theory [in Russian], Mashinostroenie, Moscow (1971).
Author information
Authors and Affiliations
Additional information
__________
Translated from Kibernetika i Sistemnyi Analiz, No. 3, pp. 58–68, May–June 2005.
Rights and permissions
About this article
Cite this article
Kirichenko, N.F., Donchenko, V.S. & Serbaev, D.P. Nonlinear Recursive Regression Transformers: Dynamic Systems and Optimization. Cybern Syst Anal 41, 364–373 (2005). https://doi.org/10.1007/s10559-005-0070-3
Received:
Issue Date:
DOI: https://doi.org/10.1007/s10559-005-0070-3