Introduction

The medical management of cardiovascular diseases, especially of arrhythmia, has become increasingly reliant upon the use of implanted electronic devices for the treatment of bradycardia or tachycardia (Winters et al. 2001; Gregoratos et al. 2004). The simple pacemakers of the 1970 gave way to the more advanced devices capable of real-time diagnosis of arrhythmia-related disorders and their treatment. The pacemaker technology and clinical practice permits the use of either single-chamber ventricular pacemakers or dual-chamber pacemakers for patients who require cardiac pacing in some indications. The single-chamber ventricular pacemakers are less expensive and their implantation is simpler than the implantation of the dual-chamber pacemakers. Several randomized studies comparing the dual-chamber “physiological” pacing to the ventricular pacing (Mattioli et al. 1998; Connolly et al. 2000; Lamas et al. 2002) have shown that the physiological pacing was more beneficial in some subgroup of patients despite the fact that both variants caused mortality, stroke and heart failures were no significant differences.

Clinical studies focusing on the quality of life with respect to the type of the pacing system implantation were also conducted. The results of the studies confirmed that the implantation of a permanent pacemaker improves health and quality of life. The quality-of-life benefits associated with dual-chamber pacing as compared with the ventricular pacing were observed only in the subgroup of patients with the sinus-node dysfunction (Lamas et al. 1998). The DAVID trial (Dual Chamber and VVI Implantable Defibrillator) demonstrated increase heart failure hospitalisation and mortality in patients programmed to the DDDR mode compared to ventricular backup pacing. The Multicenter Automatic Defibrillator Implantation Trial II (MADIT II) evoke the question of minimising the unnecessary right ventricular pacing (Wilkoff et al. 2002; Moss et al. 2002; Galley et al. 2004).

The myocardial energy demands during the cardiac pacing were studied experimentally (Montgomery et al. 1991; Portman and Ning 1995). The clinical data demonstrating the energetic changes during the pacing on the patients with dilated cardiomyopathy were shown by Baller et al. (2004). Kerckhoffs et al. (2005) carried out mathematical modelling of the right ventricular pacing and comparison with spontaneous depolarization.

In the present study we are using the numerical model of the human cardiovascular system developed in the Institute of Thermomechanics, Czech Academy of Sciences (Převorovská and Maršík 2004) with the purpose to find the parameters of the myocardial energetics during the cardiac rhythm pacing.

Methods and materials

Patients

For our research purposes the patients were designated on the basis of selective criteria. The inclusion criteria were established sick sinus syndrome and pacemaker implantation lasting more than 6 months. The exclusion criteria were left ventricle dysfunction, clinical significant valvular disease and other pathological structural heart changes. The patients with other than sinus rhythm, AV block under 110 beat/min during stimulation or bad image quality from echocardiography examination were also excluded. Our research finally involved thirteen patients with the sick sinus syndrome (eight males and five females with the average age 73 years, ranging 59–82 years). These patients with permanent dual-chamber pacemaker implantation were taken to echocardiography examination.

Study protocol

The numerical model of cardiovascular system was used to calculate the myocardial energetic parameters such as the stroke work index and the myocardial oxygen consumption for three types of pacing.

The stroke work index SWI (gm/m2) is used as a measure of myocardial contractility or work performed by the heart at every contraction. The work performed by the heart can be simply by the fluid dynamic formula \( {\text{work}} = {\text{blood volume change}} \times {\text{pressure change}}{\text{.}} \) The stroke work index of the left ventricle LVSWI is then determined by the stroke volume SV (ml), by the difference of the mean arterial pressure MAP (mmHg) and the pulmonary artery occlusion pressure PAOP (mmHg) (considered to be the indirect measure of the left atrial pressure) by the formula (http://www.lidco-ir.co.uk/html/clinical/nhp.asp)Footnote 1:

$$ {\text{LVSWI}} = 0.0136 \cdot {\left( {{\text{MAP}} - {\text{PAOP}}} \right)} \cdot {\text{SV}}/{\text{BSA}} $$
(1)

the constant 0.0136 converts the units mmHg l/m2 to gm/m2. BSA (m2) is the body surface area given by the DuBois formula (Wang et al. 1992):

$$ {\text{BSA}} = 0,007184 \cdot {\text{BW}}^{{0.425}} \cdot {\text{BH}}^{{0.725}} $$
(2)

where BW (kg) is the body weight and BH (cm) is the body height.

The myocardial oxygen consumption MVO2 (ml O2/beat) is calculated by the relationship proposed by Suga 1990, which is based on the time-varying elastance model of the ventricle. This relationship represents linear correlation between the total pressure-volume area PVA (J/beat) and MVO2 (1 ml O2 = 20 J)

$$ {\text{MVO}}_{2} = a \times {\text{PVA}} + b $$
(3)

where a is the slope coefficient and b is unloaded MVO2. PVA consists of the external mechanical work EW (J/beat) within the contraction cycle and the potential energy PE (J/beat)

$$ {\text{PVA}} = {\text{EW}} + {\text{PE}} $$
(4)

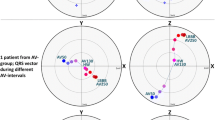
The values EW (representing the work done by the ventricle to eject blood) and PE (the work against the viscoelastic properties of the myocardium) can be estimated using the pressure-volume loops (see Fig. 1)

$$ \begin{aligned}{} & {\text{EW}} = {\left( {p_{{{\text{peakS}}}} - p_{{{\text{ED}}}} } \right)} \cdot {\left( {V_{{{\text{ED}}}} - V_{{{\text{ES}}}} } \right)} \\ & {\text{PE}} = {\left( {p_{{{\text{peakS}}}} - p_{{{\text{ED}}}} } \right)} \cdot {\left( {V_{{{\text{ES}}}} - V_{{\text{o}}} } \right)} \\ \end{aligned} $$
(5)
Fig. 1
figure 1

Ventricular pressure–volume loops

Full size image

The following symbols are used in Eq. 5:

  • p peakS (Pa) maximal value of the systolic ventricular pressure

  • p pED (Pa) end-diastolic ventricular pressure

  • V ED (m3) end-diastolic ventricular volume

  • V ES (m3) end-systolic ventricular volume

  • V o (m3) ventricular volume at zero pressure (point of intersection on the volume axis, see Fig. 1).

The input data for the numerical model, such as the anthropometrical data of the patients (weight, height) or the heart frequency, were obtained from their physical examination. The various model parameters, such as the calcium, sodium, potassium channel’s conductance, were fitted to obtain the stroke volume, blood pressure and pulmonary artery pressure established by the echocardiography examination which was performed during the spontaneous heart rhythm and the AAI, VVI, DDD pacing modes. Each mode was examined for stimulation frequencies 70, 90 and 110 beat/min. Each examination was performed 5 min after the mode change to ensure steady state. Standard views of the parasternal long-axis view and the Doppler outflow tract across the aortic valve were taken using the Agilent Sonos 5500 ultrasound device. The stroke volume was determined from the left ventricular outflow (aortic valve) diameter measured on the parasternal long-axis view and from the outflow velocity on the aortic valve measured from the apical five-chamber view (Huntsman et al. 1983; Lewis et al. 1984) by the Doppler probe. The blood pressure was measured by the sphyngomanometer for each stimulation mode. Then, the pulmonary pressure was measured by the Doppler echocardiography on tricuspid valve.

Medical Ethical Committees of the University Hospital Královské Vinohrady, Prague, approved the study protocol and the informed consent was obtained from all patients.

Mathematical model

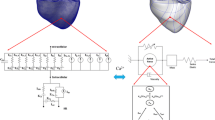
For the modelling purposes, the real cardiovascular system was compartmentalised (see Fig. 2). The 24-segment hemodynamical model (pulsating type) of the human cardiovascular system imitating the electrochemical and mechanical activity of the heart muscle was used for the numerical simulation of the myocardial workload changes during the cardiac rhythm pacing.

Fig. 2
figure 2

Scheme of the human cardiovascular system applied to heart workload calculations

Full size image

The system is approximated by twenty-four compartments, which are characterized by elasticity, resistivity and transfer of the relevant chemical components. The pulsating heart consists of the following compartments: RA—Right Atrium, RV—Right Ventricle, LA—Left Atrium, LV—Left Ventricle. The pulmonary circuit includes compartments representing the pulmonary artery (PA), arteries (Paa), capillaries (Pc), postcapillary venules (Pvv), and pulmonary veins (PV). Systemic circuit connects the aorta (Ao), systemic arteries (Saa), capillaries (Sc), head arteries (HA), capillaries (Hc), and head veins (HV). In addition, the systemic circuit includes the coronary circulation with coronary arteries (CA), capillaries (Cc), veins (CV), shunt (CS), and also the bronchial circulation with bronchial arteries (BA), left bronchial veins (BVL), capillaries (BRc), and right bronchial veins (BVR). The compartments of the pulmonary and systemic blood circulation are connected in series with the four pulsating heart compartments.

The suggested model describes the one-dimensional flow of incompressible blood through the network of elastic blood vessels. The heart compartments are considered to be made of anisotropic and viscoelastic incompressible material.

The mathematical formulation describing the blood flow in the cardiovascular system is based on the mass, energy and momentum balance. The behaviour of the cardiovascular system is described by the heart rate and by its hemodynamical variables, i.e., blood pressure, volume and flow, and by the cardiovascular parameters, such as the compliances and resistances in the corresponding compartments. The blood inertia and physicochemical variables, such as the cardiac action potential and the calcium, sodium and potassium ion concentrations, are included to support more accurate performance of the cardiovascular system. The Beeler-Reuter model (Beeler and Reuter 1977) describes the behaviour of excitable cardiac cells.

Discussion and conclusions

All experimental results obtained with the investigated patients and simulated values resulting from the applied numerical model were elaborated by the following statistical analysis. We use the null hypothesis to demonstrate the agreement or discrepancy between the values of the myocardial energetic parameters (stroke work index, myocardial oxygen consumption) obtained by the numerical simulation for the three pacing modes.

All comparisons of the data were made by the two-tailed Student’s test. The statistical analysis was performed with 5% significance level and the degree of freedom df = 24. The data for the stroke work index are expressed as the mean value ± standard deviation.

The calculated values of the stroke work index at the three pacing modes are shown in the Fig. 3. It was shown that the differences in the compared pacing modes AAI and VVI and the modes DDD and VVI are statistically significant (P < 0.05). The comparison of the stimulation modes DDD and AAI shows that the differences are statistically insignificant (P > 0.05).

Fig. 3
figure 3

Stroke work index calculated by the numerical model of cardiovascular and respiratory system

Full size image

The calculated values of the myocardial oxygen consumption for three pacing modes are demonstrated in the Fig. 4. The myocardial efficiency, which is an important factor for heart performance, changes according to the stimulation mode. The changes resulting from the hemodynamical model fitting by the well-measurable data, i.e., heart rate, stroke volume, systolic pulmonary artery pressure, systolic and diastolic aortic pressure. The conclusion is that the difference between the modes AAI and VVI and the modes DDD and VVI is statistically significant (P < 0.05). The statistical analysis of the AAI and DDD modes indicates that the compared data are not significantly different (P > 0.05).

Fig. 4
figure 4

Myocardial oxygen consumption calculated by the numerical model of cardiovascular system in various pacemaker modes

Full size image

From the comparison of the obtained numerical values for the stroke work index between the AAI and VVI pacing modes and between DDD and VVI modes it follows that the differences are statistically significant (P < 0.05). The results are consistent with the published data (Leclercq et al. 1995; Nielsen et al. 1998). The results of the statistical analysis for the AAI and DDD stimulation modes show that the differences between the compared groups are statistically insignificant (P > 0.05). These results are consistent with the clinical observation where can achieve a similar clinical outcome in AAI and DDD modes in this group of patients (Masumoto et al. 2004). The increase of the stroke work index in AAI or DDD modes was caused by saving the AV synchrony in the patient with the normal left ventricle systolic function. During the AAI pacing mode the implantation of the pacemaker is easier. This fact supports the clinical superiority of the AAI mode against the DDD mode in the sick-sinus group patients with preserved left ventricular function.

The results of the comparison of the obtained numerical values for the myocardial oxygen consumption between the AAI and VVI and between DDD and VVI modes show that the difference between the modes is statistically significant (P < 0.05). The increase of the myocardial oxygen consumption corresponds to the increase of the stroke work index. From the comparison of AAI and DDD modes we can see that the difference is statistically insignificant (P > 0.05).

The insufficient number of the designated subjects gives the limitation of our research study because very strict exclusion criteria exist for the concomitant disease. Many pacemaker patients were not eligible for echocardiography examination because they had hypertension, left ventricle dysfunction or valvular disease.

We conclude that mathematical modelling of the cardiovascular system is a recommended method for the estimation of the myocardial energy demand in patients with heart diseases.