Analysis of Vertical Turbulent Heat Flux Limit in Stable Conditions with a Local Equilibrium, Turbulence Closure Model

Abstract

Assuming that the vertical turbulent heat flux vanishes at extremely stable conditions, one should expect its maximal absolute value to occur somewhere at moderate stability, between a neutral and extremely stable equilibrium. Consequently, in some situations duality of solutions may be encountered (e.g. two different values of temperature difference associated with the same values of heat flux and wind speed). A quantitative analysis of this feature with a local equilibrium Reynolds-stress model is presented. The fixed-wind / fixed-shear maximum has been identified both in the bulk and in single-point flux–gradient relationships (that is, in the vertical temperature gradient and wind-shear parameter domain). The value of the Richardson number corresponding to this maximum is derived from the model equations. To study the possible feedback in strongly stable conditions, weak and intense cooling scenarios have been simulated with a one-dimensional numerical, high-resolution atmospheric boundary-layer model. Despite the rapid cooling, flow decoupling at the surface has not been observed; instead, a stability-limited heat flux is maintained, with a gradual increase of the Richardson number towards the top of the turbulent layer, with some signs of oscillatory behaviour at intermediate heights. Vertical changes of wind shear and the Brunt–Väisälä frequency display a remarkably non-monotonic character, with some signs of a gradually developing instability.

1 Introduction

At extreme stability, the vertical downward heat flux is supposed to vanish due to the suppression of turbulence by buoyancy forces and in spite of the presence of a large vertical temperature gradient. As the heat flux is also null at neutral conditions, a maximum should be present somewhere in the intermediate range of variability of an arbitrary stratification parameter. For example, if turbulence ceases at a critical value of the Richardson number (either gradient, or flux), there should be a maximum of downward heat flux¹ found at a certain value of this number (less than critical) and an identical value of the heat flux (at two different values of stability parameter) should be found on both sides of the maximum’s location. In other words, the existence of a critical value of a controlling equilibrium parameter is a sufficient condition for the presence of such a maximum.

While the above statement seems logical, two remarks should be made. First, it is not clear to what extent the stably stratified turbulent flows can be characterized with a single “traditional” stratification parameter such as the Obukhov parameter or the Richardson number. Second, it is not certain that the heat flux actually vanishes in extremely stable conditions. These reservations should be made, as many recent studies undermined the belief in the existence of the critical gradient Richardson number (e.g. Galperin et al. 2007; Zilitinkevich and Esau 2007; Mahrt 2010). Still, earlier Malhi (1995), Ohya et al. (1997) and Mahrt et al. (1998) proposed to identify a regime with weak or occasional turbulence, termed a “very stable boundary layer” (VSBL). In a VSBL, the transport of heat is maintained by processes other than continuous turbulence, thus the similarity theory becomes ineffective (Mahrt et al. 1998). Currently, the VSBL behaviour remains insufficiently understood, and research on this subject continues (e.g. van de Wiel et al. 2012a).

The presence of the downward heat flux maximum implies the existence of a limit to the turbulent transport, i.e. for a given mechanical forcing² it might become impossible to increase the heat flux beyond a certain value, no matter how large the ground surface cooling rate would be.³ Is this limitation directly related to the rapid “runaway” surface cooling events, resulting in shallow and intense surface inversions? Are such flux-limiting conditions characteristic of the surface layer or may they also occur in the outer part of the stable boundary layer? And, if so, is there a natural tendency to maintain maximum flux in a broader region (by self-adjustment of profiles), or do the occurrences have a rather incidental character? Further, if a duality of solutions exists is it associated with spontaneous transitions between the alternate regimes? Can we find a physical interpretation of the two alternate solutions, associated with both the smaller and the larger temperature gradient? Is any one of them, for any reason, preferred in nature? And, if so, which of these solutions should be chosen in models, driven by a specified heat flux at the boundary?

Many of these questions have already been addressed in several studies. Taylor (1971) was likely the first to notice the duality of solutions to the problem of finding the friction velocity, given the values of surface heat flux and wind speed. Then, he conjectured that only one of these solutions, that associated with a larger momentum flux, was a hydrodynamically stable one and should be chosen. While the latter statement encountered criticism (Arya 1972; Carson and Richards 1978), the existence of the maximum was corroborated by experimental evidence (Malhi 1995; Mahrt 1998; Basu et al. 2006; Sorbjan 2006). Recently, van de Wiel et al. (2007) revisited Taylor’s conjecture, showing the stability of the continuously turbulent solution (corresponding to Taylor’s solution associated with the larger momentum flux) by linear stability analysis. Then, Basu et al. (2008) considered two types of the boundary condition at the surface, set either by prescribing the surface temperature or prescribing the surface heat flux. While their recommendation was clearly in favour of the first option, one might note that the system considered in their work is considerably simpler than the surface heat budget treatment in numerical weather prediction models, typically involving a module describing energy transport in soil. An analysis of such a system is still awaited.

Numerical errors in atmospheric numerical models often obscure mathematical properties of the exact solution. Uncontrolled oscillations frequently encountered in stable stratification have directed attention to the stability of numerical integration. Remedies for these problems were proposed by Kalnay and Kanamitsu (1988) as well as by Girard and Delage (1990). These schemes proved effective in damping oscillations arising in the surface energy budget and in the turbulent kinetic energy budget, correspondingly. McNider et al. (1995) and Derbyshire (1999) investigated boundary instability in the atmosphere-land system under strong radiative cooling conditions. They concordantly identified instability mechanisms present in simple formulations of such a coupled system. Further studies on the turbulence collapse, decoupling of the flow, and the controlling factors continue (van de Wiel et al. 2012a, b).

An apparent limitation of most of the above listed studies lies in using first-order turbulence closure, either in the form of prescribed flux–gradient relationships (log-linear similarity functions), or of specification of eddy transfer coefficients (typically, resting on a prescribed dependence on the gradient Richardson number, $Ri$). Hence, the quantitative results obtained so far reflect to a certain degree the arbitrary choice of particular relations rather than the underlying physics. Also, it is not clear to what extent conclusions from these studies are applicable to more complex models, based on higher-order turbulence closure schemes. This issue seems to be important, as many models applied in a wide range of geophysical problems, from microscale and mesoscale research through numerical weather forecasting, to global circulation models of the ocean and atmosphere, utilize a more complex yet practical and effective approach, viz. simplified second-order turbulence closure schemes. Since the interest in model performance in stable conditions is growing, properties of such turbulence models deserve attention.

In the present study, past research on the heat maximum issue is supplemented through the analysis of the solutions of a local equilibrium Reynolds-stress model. In contrast to the majority of earlier studies, the present analysis is not restricted to the surface layer. Both the bulk surface-layer flux–finite difference relationships as derived from the turbulence model (Łobocki 1993), and the solutions of a high resolution, one-dimensional numerical boundary-layer model, are investigated.

The particular turbulence model selected for this study belongs to the Mellor–Yamada family of turbulence closure models (Mellor and Yamada 1982), as used in numerical weather prediction (e.g. the U.S. NCEP “Eta”/NAM model, (e.g. Janjić 1990; Gerrity et al. 1994), the Japanese JMA-NHM model (Saito et al. 2007), mesoscale atmospheric research (e.g. the WRF model (Sušelj and Sood 2010; Foreman and Emeis 2012)), ocean modelling (e.g. Blumberg and Mellor 1987; Kantha and Clayson 1994; Burchard and Bolding 2001), and global atmospheric models (e.g. Sirutis and Miyakoda 1990). The level-2 closure scheme used herein (Mellor 1973; Mellor and Yamada 1974) can be considered a local equilibrium simplification of the more complex level-3 and level-2.5 turbulence closures used in these models. Certain differences may include the specification of the master length scale and values of model constants as used in individual implementations; in such cases, the present paper may serve as a methodology.

In the context of the Mellor–Yamada model stability issues, it is necessary to mention a recent perturbation analysis by Deleersnijder et al. (2008), specifically regarding the level-2.5 version (Yamada 1977) and its modifications (Hassid and Galperin 1983; Galperin et al. 1988). In his study, an eigenmode analysis of the linearized version of the turbulence model was presented. However, non-linear effects such as a possible duality of solutions remained beyond the scope of the study.

2 Model Calculations

As a thorough description of the turbulence model examined here is available elsewhere (e.g. Mellor 1973; Mellor and Yamada 1974; Yamada 1975; Mellor and Yamada 1982; Nakanishi 2001), we refer to relevant features only.

2.1 Model Constants

While the original selection of model constants (Mellor 1973) had been based on the results of early laboratory experiments, numerous modifications aiming at a better fit to atmospheric data and large-eddy simulation results were later proposed (e.g. Mellor and Yamada 1982; Nakanishi 2001; Foreman and Emeis 2012). As the original set of constants results in a turbulence cut-off at $Ri_c=0.21$, we have opted here for another set, based on a fit to atmospheric data (Łobocki 1993) that shifts $Ri_c$ to 0.56. These are

$$\begin{aligned} \left( A_1,\, A_2,\,B_1,\,B_2,\,C_1\right) = \left( 0.69, 0.52, 16.6, 7.9, 0.06\right) . \end{aligned}$$

Note that this choice leads to a quantitative rather than a qualitative change in model behaviour.

2.2 Local Relationships

The turbulence closure scheme provides local relationships between the two controlling parameters, the vertical gradients of both wind speed $U$ and potential temperature $\Theta$ that may be expressed as,

$$\begin{aligned} \overline{u^{\prime }w^{\prime }}&= - S_M(R_F) q \ell \frac{\,\mathrm{d}{U}}{\,\mathrm{d}{z}},\end{aligned}$$

(1)

$$\begin{aligned} \overline{w^{\prime }\theta ^{\prime }}&= - S_H(R_F) q \ell \frac{\,\mathrm{d}{\Theta }}{\,\mathrm{d}{z}}, \end{aligned}$$

(2)

where $\overline{u^{\prime }w^{\prime }}$ and $\overline{w^{\prime }\theta ^{\prime }}$ denote the vertical kinematic turbulent fluxes of momentum and heat, respectively; $q^2$ is twice the turbulent kinetic energy per unit mass (TKE), $\ell$ is the master length scale, and $S_M$ and $S_H$ are non-dimensional functions of the flux Richardson number $R_F$. These functions are derived from the turbulence model, as well as the relationships between the flux and the gradient Richardson numbers; for details, see e.g. Mellor and Yamada (1982). Further, in this model formulation the TKE normalized by the momentum flux does not depend on the master length scale. Hence, the calculation of fluxes can be accomplished once the gradients are given, and the master length scale is specified. As the fluxes are simply proportional to this length scale, their patterns are not affected by the dependence of the length scale on stratification. For the purpose of this study, we shall assume that the master length scale depends solely on the height and is not directly affected by stratification.⁴ Hence, it is sufficient to present here the distributions of fluxes divided by the master length scale.

Figure 1 displays the vertical turbulent heat flux, divided by the master length scale, as a function of two parameters: the wind shear

$$\begin{aligned} S=\frac{\text {d}U}{\text {d}z}, \end{aligned}$$

(3)

and the Brunt–Väisälä frequency

$$\begin{aligned} N=\sqrt{\beta \frac{\text {d}\Theta }{\text {d}z}}~. \end{aligned}$$

(4)

A pencil of lines passing through the coordinate system origin (broken lines) marks constant values of the gradient Richardson number,

$$\begin{aligned} Ri=\frac{N^2}{S^2}~. \end{aligned}$$

(5)

The stippled region shows the supercritical gradient Richardson number. Solid lines are the isopleths of the kinematic vertical turbulent heat flux, divided by the unit master length scale, $\overline{w^{\prime }\theta ^{\prime }}/\ell$. As these isopleths cannot enter the supercritical $Ri$ regime, they must asymptotically align with the boundary of the supercritical regime. Hence, a maximum value of heat flux for a fixed wind speed must exist. However, the existence of the critical Richardson number is not a necessary condition here; should another inflection point be present on an isopleth, such an isopleth might asymptotically align with the horizontal axis ($S=0$).

Fig. 1

Kinematic vertical turbulent heat flux, per unit master length scale $\overline{w^{\prime }\theta ^{\prime }}/\ell [\hbox {Ks}^{-1}]$, as a function of wind shear $S$ and the Brunt–Väisälä frequency $N$, calculated using the Mellor–Yamada level-2 model. See text for a description of details

It is worth noting that the isopleths of the gradient Richardson number co-lineate with the isopleths of the flux Richardson number, the Obukhov parameter, and the TKE scaled with the momentum flux, as all of these quantities are uniquely related. Further, the maxima are apparently aligned along a straight line corresponding to a constant value of the Richardson- number. To find this value, let us start with the conventional form of the flux–gradient relationship,

$$\begin{aligned} \frac{\,\mathrm{d}{U}}{\,\mathrm{d}{z}}&= \left( \frac{u_*}{\kappa \,z}\right) \,\phi _m,\end{aligned}$$

(6)

$$\begin{aligned} \frac{\,\mathrm{d}{\Theta }}{\,\mathrm{d}{z}}&= \left( \frac{T_*}{\kappa \,z}\right) \,\phi _h, \end{aligned}$$

(7)

where $u_*$ and $T_*$ are the velocity and temperature scales respectively; $\phi _m$ and $\phi _h$ are universal non-dimensional gradients that are dependent on a single equilibrium parameter, either one of those listed above. For convenience, let us choose their dependence on $Ri$. By multiplying these equations side-by-side, one obtains

$$\begin{aligned} {u_*}{T_*}= {(\kappa z)}^2 \frac{\,\mathrm{d}{U}}{\,\mathrm{d}{z}} \frac{\,\mathrm{d}{\Theta }}{\,\mathrm{d}{z}}\, \phi _m^{-1}\,\phi _h^{-1}. \end{aligned}$$

(8)

Let us denote $\phi _m^{-1}\,\phi _h^{-1}$ by $\Phi (Ri)$. By equating the partial derivative of $Ri$ with respect to $\eta =\,\mathrm{d}{\Theta }/\,\mathrm{d}{z}$, to zero, we obtain

$$\begin{aligned} \Phi + \eta \frac{\,\mathrm{d}{\Phi }}{\,\mathrm{d}{Ri}}\frac{\partial {Ri}}{\partial {\eta }}= \Phi + Ri\, \frac{\,\mathrm{d}{\Phi }}{\,\mathrm{d}{Ri}} = 0, \end{aligned}$$

(9)

which can be reformulated as

$$\begin{aligned} \frac{\,\mathrm{d}\phi _m}{\phi _m} + \frac{\,\mathrm{d}\phi _h}{\phi _h} = \frac{\,\mathrm{d}Ri}{Ri}. \end{aligned}$$

(10)

Derbyshire (1999) considered an analogous condition (however in the context of a simpler turbulence closure scheme) as a fixed-shear criterion for instability (FSCI). He noted that a fixed shear is rather unlikely to persist during cooling, hence the FSCI should not be regarded as a sufficient condition for the development of instability. Nevertheless, a limited positive feedback may still occur. One may note that if non-dimensional gradients $\phi _m$ and $\phi _h$ are sole functions of $Ri$, their particular forms would determine the value of $Ri$ corresponding to the location of the maximum. Definitions of flux and gradient Richardson numbers, together with Eqs. 6 and 7 imply

$$\begin{aligned} \frac{\,\mathrm{d}\phi _m}{\phi _m} + \frac{\,\mathrm{d}Ri}{Ri} = \frac{\,\mathrm{d}\phi _h}{\phi _h} + \frac{\,\mathrm{d}R_F}{R_F}, \end{aligned}$$

(11)

so that, recalling (1), as there is no explicit dependence of master length scale on the Richardson number in the adopted model,

$$\begin{aligned} -\frac{1}{2}\,\frac{\,\mathrm{d}R_F}{R_F} = \frac{\,\mathrm{d}S_M}{S_M} + \frac{\,\mathrm{d}q_n}{q_n} \end{aligned}$$

(12)

where $q_n=q/u_*$. The TKE budget equation yields

$$\begin{aligned} q_n = \left[ \frac{B_1(1-R_F)}{S_M}\right] ^{1/4} \end{aligned}$$

(13)

and the $S_M$ function is given by (e.g. Mellor and Yamada 1982),

$$\begin{aligned} S_M = 3\,{A_1} \, \frac{a+b\,R_F}{c+d\,R_F} \, \left( \gamma _1-\gamma _2\,\frac{R_F}{1-R_F}\right) , \end{aligned}$$

(14)

where $a=B_1(\gamma _1-C_1),\,b=-(a+6 A_1 +3 A_2),\,c=B_1\gamma _1,\,d=3 A_1-B_1(\gamma _1+\gamma _2),\,\gamma _1=\frac{1}{3}-\frac{2A_1}{B_1},\,\gamma _2=\frac{6 A_1}{B_1 } + \frac{B_2}{B_1}$. This leads to

$$\begin{aligned} \frac{2 - 3 R_F}{3\, R_F\, (1-R_F)}&= \frac{\gamma _2}{\left[ \gamma _1-(\gamma _1+\gamma _2)\, R_F\right] \,(1-R_F)} \nonumber \\&- \frac{b}{a + b\, R_F} + \frac{d}{c + d\, R_F}, \end{aligned}$$

(15)

which can be readily solved. For model constants listed in Sect. 2.1, $R_F\approx 0.126$, which corresponds to $Ri\approx 0.144$, and $z/L\approx 0.178$. The last value fits the location of a fixed wind-speed maximum at $z/L\approx 0.2$ as found in experimental data of Malhi (1995) (see his Fig. 2) quite well.

Fig. 2

Surface vertical heat flux $\rho \,c_p\,\overline{w^{\prime }\theta ^{\prime }}$ calculated using the Mellor–Yamada level-2 model

2.3 Surface Layer

Calculation of surface fluxes involves an integration of vertical gradients in order to express fluxes in terms of bulk parameters, i.e. wind-speed and temperature differences across a certain height interval. To accomplish this goal, we used a method presented earlier (Łobocki 1993). Figure 2, inspired by Carson and Richards (1978), presents the heat flux as a function of wind speed at 10 m and a temperature difference between this height and the surface, calculated using a roughness length $z_0=10^{-3}$ m. The observations are qualitatively similar to those from the previous section. Taking a value of heat flux of 20 $\mathrm{W\,m^{-2}}$ as an example, we see that this value, associated with a wind speed of $5~\mathrm{m\,s^{-1}}$, may occur either at the temperature difference of 1.5 K, or at a much larger value 8 K. In the weak wind regime, say below 1 $\mathrm{m\,s^{-1}}$, the model predicts turbulence to be maintained only at small temperature differences below 0.5 K, and the difference between the two solutions corresponding to a given wind speed is also small.⁵

The analysis presented in Sect. 2.2 suggests dividing the $(N, S)$ domain in Fig. 1 into three regions: a supercritical $Ri$ area, and the areas of larger and smaller values of temperature gradient corresponding to the same values of wind shear and heat flux, separated with a $Ri=0.144$ line. This delimitation corresponds to a crest line passing through inflection points at all the isopleths drawn on Fig. 2. One might be tempted to associate this division with slow and rapid cooling scenarios in the development of surface-based inversions. That is, while the slow cooling should perhaps result in a relatively deep inversion with a small temperature difference, the rapid scenario would lead to a shallow and intense inversion. It is then interesting to determine whether these scenarios are actually associated with the discussed duality of solutions, and whether setting one of the regimes at the surface layer would also imply a similar regime aloft. To investigate this matter, we resort to simulations with a numerical boundary-layer model (see below).

2.4 Boundary Layer

The simple, one-dimensional model of the atmospheric boundary layer used here includes prognostic equations of momentum and heat transport, and a fully diagnostic turbulence closure. Radiative and condensational processes were not considered. The system of equations is solved with a semi-implicit algorithm consisting of an explicit calculation of the TKE and eddy transfer coefficients, and a fully implicit Crank–Nicholson scheme applied to the transport equations. A log-linear transformation of the vertical coordinate (Taylor and Delage 1971) enables a sufficient resolution for the large vertical gradients present near the ground, with the grid spacing of the order of $z_0$. However, an alternative formulation, utilizing “effective” eddy transfer coefficients (Łobocki 1993) is also available, allowing for grid spacing of $\approx$10 m near the ground, typical of mesoscale models. In fact, this feature is essential for the present study, as much of the attention is focused on the interactions between the surface layer, the parametrizations applied thereto, and the performance of the turbulence closure scheme as applied to the outer part of the boundary layer.

To assess this feature, let us compare results obtained with the following two model set-ups. The first assumes explicitly resolved transport on a grid containing 100 nodes, with vertical spacing varying from $8\times 10^{-3}$ m near the ground, to roughly 20 m in the outer part of the boundary layer. To obtain smooth solutions, without oscillations in the surface heat-flux temporal variability, it was necessary to use a rather short timestep, as small as 1 s. In the second set-up, the lowermost 20 levels were replaced by a bulk surface-layer parametrization derived from the same turbulence closure scheme, and the timestep was increased to 60 s.

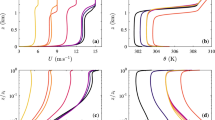
Figure 3 presents results of a simulation of the boundary-layer development during Day 33 of the Wangara experiment (Clarke et al. 1971), with both formulations. Green marks denote the configuration employing the bulk parametrization, while the red ones mark the explicit set-up. As might be seen, the match between the two versions is nearly perfect.

Fig. 3

A comparison of the high-resolution finite-difference solution (red) and the integral surface-layer parametrization (green). Simulation of the boundary-layer evolution during Day 33 of the Wangara experiment with the level-2 Mellor–Yamada model (constants as in Mellor and Yamada (1982)). Squares 1200 LST, triangles 2100 LST, circles 0300 LST on day 34. Right pane focuses on the lowest 50 m

3 Results and Discussion

To investigate the “slow” and “rapid” cooling scenarios, several model runs were performed using various surface cooling rates imposed by a prescribed rate of change of the surface temperature. Initial conditions and synoptic forcing were taken from the aforementioned Wangara simulations. Figure 4 presents a series of potential temperature profiles at 2100, 2400 and 0300 LST (left pane) and corresponding hodographs in the $(N,\,S)$ space (right pane). As might be seen from the potential temperature profiles, the nocturnal cooling is very weak, with the surface temperature decreasing by $\approx$2 K in 6 h. The data points at the hodographs placed in the upper part of the frame (highest wind-shear values) correspond to the lowermost model levels; near the inversion top, both the wind shear and the temperature gradient diminish, leading to a nearly critical regime. It is worth noting that the Richardson number increases with height, and that most of the data points appear to lie in the smaller temperature gradient subdomain. However, near the inversion top, the hodographs cross the $Ri=0.144$ line, apparently smoothly entering the regime of the larger temperature gradient solution.

Fig. 4

Weak surface cooling scenario. Top potential temperature profiles at 2100 (red squares), 2400 (blue triangles) and 0300 (green circles) LST. Bottom hodographs of the solutions in the $\left( N, S\right)$ parameter space. Labels in the plot denote grid levels (m). High-resolution finite-difference Mellor–Yamada level-2 model, modified constants (Łobocki 1993)

The intense cooling scenario (4 K in 6 h) leading to the formation of an approximately 130 m deep, 14 K intense surface inversion, reveals an interesting phenomenon (Fig. 5). While the near-surface data lie below the value of $Ri \approx 0.144$, there is a zone where the temperature gradient increases with height, with little change in the wind shear. One might call these conditions a limitation regime as, for a given dynamical forcing, the growth of the heat flux becomes impossible at a cost of increasing temperature gradient. In contrast with Taylor’s premise, this limitation regime sublayer may arise aloft within a stably stratified layer, that is, under the indirect influence of boundary forcing. In our simulations, the flow is not decoupled at the surface, but rather the critical $Ri$ regime is maintained in the top part of the weakly turbulent boundary layer, due to the lack of shear in the residual layer. Underneath, there is an expanding sublayer where limitation conditions occur; however, the existing heat flux is sufficient to maintain a slow growth.

Fig. 5

Intense surface cooling scenario. Top potential temperature profiles at 2100 (red squares), 2400 (blue triangles) and 0300 (green circles) LST. Bottom hodographs of the solutions in the $\left( N, S\right)$ parameter space. Labels in the plot denote grid levels (m). High-resolution finite-difference Mellor–Yamada level-2 model, modified constants (Łobocki 1993)

Temporal and vertical changes of stability parameters in the intense cooling scenario are illustrated in Figs. 6 and 7. In response to the surface cooling, both the wind shear and temperature gradient decrease within the lowest 10 m; however, an opposite tendency is present in the upper part of the boundary layer. Eventually, non-monotonic vertical profiles are established (Fig. 7). Nevertheless, concurrent changes in both parameters remain roughly balanced, so that the temporal variations of the resulting Richardson number remain small (Fig. 6), and the vertical profiles remain monotonic. Noteworthy is that the most pronounced changes of $Ri$ take place at intermediate heights, 1–10 m, while $Ri$ in both the upper and the near-surface layers remains steady after 2000 LST. One may also note developing oscillations having a 3-h period and growing amplitude. While they might have been excited by the inertial wind oscillation, their period does not correspond to any external forcing. Hence, a specific internal mechanism causing free oscillations is apparently present. However, due to the simplicity of the model adopted in this study, a quantitative comparison of this result to the observed features of turbulence under strongly stable conditions seems too risky.

Fig. 6

Variation of the gradient Richardson number in the intense cooling scenario, at different heights (from bottom to top): red 0.38 m, magenta 1.12 m, purple 3.2 m, blue 8.6 m, green 20.4 m, orange 40.8 m

Fig. 7

Vertical profiles of wind shear ($S$, left pane) and Brunt–Väisälä frequency ($N$, right pane) in the intense cooling scenario. Red squares 2100 LST, blue triangles 2400 LST, green circles 0300 LST

4 Summary and Conclusions

The constant wind shear, heat-flux maximum discussed in previous studies of the stably stratified surface layer has been analyzed with a turbulence closure model. The existence of such a maximum is implied by the existence of a critical value of the gradient Richardson number. However, lack of such a critical value does not preclude the existence of the maximum.

Derbyshire (1999) wrote “Some SBL schemes derived from micrometeorological research seem to allow a decoupling behaviour when implemented in NWP. That is, turbulence dies out from the ground upwards. Such decoupling of the surface from atmospheric fluxes can permit dramatic and possibly unrealistic falls in surface temperature.” This study shows a different pattern, with the changes of static stability and shear gradually propagating through the stable boundary layer. Noteworthy is that the passage between the two regimes (as delineated by the ‘crest’ of the location of heat-flux extrema in Fig. 5) is gradual, without any signs of rapid swapping between the dual solutions. Apparently the intrinsics of the Mellor–Yamada level-2 turbulence closure scheme are not prone to induce instabilities.

It has been pointed out that the existence of the heat-flux maximum is not an exclusive feature of the surface layer. Rather, it may occur, and may even be more frequent, in the upper part of the stable boundary layer. As the term ‘maximum’, as used here, corresponds to the value that cannot be exceeded under certain circumstances, one may also understand it as a limiting value of the heat flux. We have found locations of such constant wind shear, heat-flux maxima at a certain value of $Ri$, and expressed it in terms of model constants. When this value is exceeded, a hypothetical growth of vertical temperature gradient under constant wind shear cannot result in a further increase in the heat flux; therefore, the term limitation regime is proposed. Model calculations show that such a limitation regime may become established in the upper part of the boundary layer, rather than arising immediately near the ground. A viable explanation of the lack of decoupling at the surface may lie in the domination of the wind-shear production over buoyancy sink terms in the turbulent kinetic energy budget, and in differences in the heat and momentum transfer efficiencies. At the top of the stable boundary layer, which gradually encroaches lower portions of the residual layer, the shear is near zero, so even with small values of the potential temperature gradient, the gradient Richardson number is high. Near the surface, wind shear dominates over the buoyancy, so that the heat transport is maintained despite the stratification stability. In the bulk of the boundary layer, a gradual self-adaptation of profiles takes place. Noteworthy is a non-monotonic, but proportional, vertical variability of wind shear and temperature gradient, and a gradual, almost evenly distributed, variation of the Richardson number in response to surface cooling. It needs to be noted that this pattern of evolution is idealized, since it reflects: (1) the features of a particular model used here; (2) particular forcing and initial conditions, highly regular in this study. Further work should include simulations of selected field data with a single-column model and large-eddy simulations, experimenting with alternative model formulations (in particular, the master-length scale specification), and investigating rapid cooling events in numerical model weather forecasts.