1 Introduction

Standard tools for Probabilistic Seismic Hazard Assessment (PSHA) estimate the ground motion due to an earthquake by means of Ground Motion Models (GMMs), which provide the median and the associated aleatory variability of ground motion Intensity Measures (IMs) as a function of source, path and site parameters for a given site. As GMMs consider IMs at all sites as independent variables, they do not provide a description of the correlation structure of ground motion IMs at multiple sites. The quantification of the spatial correlation properties of ground motions is of fundamental importance for estimating risks to spatially-distributed infrastructures and portfolios of buildings. For instance, Iervolino (2013), Sokolov and Ismail-Zadeh (2016) and Sokolov and Wenzel (2019) showed the differences between site-specific and multiple-site PSHA, underlining the importance of considering regional hazard for the calculation of aggregate risk.

Despite the progressive increase of studies on spatial correlation in earthquake ground motions over the last 20 years, debates on the factors affecting spatial correlation still continue. Schiappapietra and Douglas (2020) provide a thorough literature review, critically exploring the main facets of spatial correlation that need to be addressed. Among these aspects, they reported dependence on: (1) the estimation approach; (2) the fitting method; (3) the earthquake magnitude (Mw); (4) the vibration period; (5) local site-effects; and (6) ground motion prediction models. In this regard, a valuable contribution can be also found in Baker and Chen (2020), who recently propose an alternative approach to assess the uncertainty in spatial correlation models in terms of both true and estimation variability. These authors suggest that differences in terms of true variability in correlation among well-recorded and poorly-recorded events are negligible. On the contrary, the estimation uncertainty is inversely correlated to the number of available stations, as demonstrated also by Schiappapietra and Douglas (2020) and Infantino et al. (2021). Moreover, spatial correlation models are usually grounded on the hypothesis of stationarity and isotropy. Namely, the correlation between any pairs of sites with equal separation distance is the same, independently of the source-to-site distance and orientation (Goovaerts 1997; Diggle and Ribeiro 2007). However, different studies (e.g. Chen and Baker 2019; Huang et al. 2020; Infantino et al. 2021) demonstrate the presence of anisotropy in spatial correlation, which tends to be stronger for long-period IMs. Garakaninezhad and Bastami (2017) examined the effects of focal mechanism, Vs,30 (time-averaged shear-wave velocity in the upper 30 m), magnitude and hypocentral distance on the anisotropy ratio and angle, and reported a positive correlation between the anisotropy ratio of high frequency IMs and that of Vs,30 as well as with Mw. Similar conclusions were also drawn by Abbasnejadfard et al. (2020).

Our knowledge on the factors mostly affecting ground motion spatial correlations is partially hampered by both the shortage of ground motion recordings and the possibility of having sufficient data from specific environments. In this framework, 3D Physics-Based ground motion Simulations (3D PBSs) could be employed to provide further insights into earthquake ground motion spatial correlations. 3D PBSs provide spatially-distributed estimates of region-specific ground motions, as they are based on sufficiently detailed models of the seismic source, propagation path and near-surface geology. 3D PBSs enable issues due to the lack of observations to be overcome, especially in the near-source region. They also allow investigation of the impact of factors such as local-site conditions, magnitude, slip distributions and hypocentral locations, on the spatial correlation in a detailed way that is not feasible with earthquake recordings. Infantino et al. (2021) studied the spatial correlations of broadband 3D PBSs for seven different case-studies (Po plain, L’Aquila, Marsica, Sulmona, Norcia—Italy; Thessaloniki—Greece; Istanbul—Turkey) and found a strong variability in terms of correlation lengths due to a strong dependence of the ground motion spatial variability on both local-site and rupture-propagation effects. Stafford et al. (2018) investigated the impact of source kinematics on spatial correlation using finite difference simulations, demonstrating that the rupture process of scenarios of equal magnitude contribute markedly to the correlation length variability. Likewise, Chen and Baker (2019), taking advantage of the CyberShake database, reported supporting evidence of the impact of source and path effects on spatial correlation.

In this context, we use 3D broadband PBSs to address some of the still open questions on earthquake ground motion spatial correlation. We choose the 3D PBS of the 30th October Mw 6.5 Norcia (Central Italy) earthquake as a case study (Özcebe et al. 2019). The authors generated the simulations through the spectral element code SPEED (http://speed.mox.polimi.it, Mazzieri et al. (2013)), which replenishes the frequency spectrum at the high frequencies by using a novel method that makes use of Artificial Neural Networks (Paolucci et al. 2018). The numerical code and its ability to reproduce ground motion spatial correlations have already been validated in different studies (e.g. Stupazzini et al. 2009; Paolucci et al. 2015, 2016, 2018; Infantino et al. 2021). In addition to the 3D PBS of the Mw 6.5 Norcia event, we generate several scenarios by varying either the slip distribution or the hypocentral location to explore different spatial correlation properties, such as the dependency on the rupture process and magnitude. While relaxing the hypothesis of isotropy, we explore possible preferential directions of the ground motion spatial variability as well as the relationship of such directions with the source mechanism and frequency content of the ground motion.

Furthermore, spatial correlation models are usually calibrated on the horizontal component of the ground motion and little effort has been directed towards other components, such as the fault-normal (FN) and the fault-parallel (FP) directions as well as the vertical component (Garakaninezhad and Bastami 2019; Infantino et al. 2021). In the near-field, the ground motion is strongly affected by both the slip distribution and fault mechanism, which can cause a significant polarization of the ground motion (Bray and Rodriguez-Marek 2004). Somerville et al. (1997) demonstrated that the ratios between the FN and FP components of the motion are larger than 1 in the proximity of the fault due to rupture directivity effects. Consequently, we extend our studies to the vertical (Z), FN and FP components, in addition to the horizontal one (defined as the geometric mean of the two horizontal components, geoH), to identify diagnostic spatial correlation features for each component.

2 3D Physics-based broadband ground motion simulations

In recent years, major advances in parallel high-performance computational resources have allowed the development of high-order numerical methods to model the seismic response of 3D heterogeneous media under realistic tectonic and geomorphological conditions. 3D PBSs embody physical and sufficiently accurate models of the seismic source, path and local-site effects to provide region-specific earthquake ground motion predictions. These estimates are, however, reliable only in the low-frequency spectrum (up to 1–1.5 Hz) due to the current limitations in: (1) computational capabilities and (2) detailed knowledge of the geological medium that would enable modelling the propagation of short wavelengths. In this study, we use the spectral element code SPEED to generate spatially distributed broadband ground motions for different scenarios. SPEED is designed to solve 3D seismic wave propagation problems in complex heterogeneous media. Its main advantage lies on its capability to generate realistic broadband ground motion waveforms by means of a novel approach based on Artificial Neural Networks (Paolucci et al. 2018).

2.1 3D numerical modelling

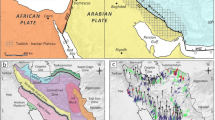
3D numerical simulations require three main inputs: (1) a crustal velocity model, (2) a geotechnical model of local shallow geological structures (e.g. the Norcia basin), and (3) a kinematic slip distribution along the causative fault. The numerical model of the Norcia area (Fig. 1) was produced in a previous project and the reader should refer to Özcebe et al. (2019) for further details. We note here that the results of the 3DPBS for the Norcia case were compared against the available recordings and geodetic measurements to test the goodness of fit of the simulated data. While using the same crustal velocity model and geotechnical setting throughout the analysis, we implement different kinematic source models to allow for the magnitude, slip distribution and hypocentre location to vary among the considered scenarios. The full set of source parameters for the different case studies are given in Sect. 2.3. The final spectral element computational domain of the Norcia area, which includes the source and velocity models as well as the surface topography (Fig. 1a), extends over an area of \(40 \times 50 \times 21~\;{\text{km}}^{3}\) and consists of more than 350,000 hexahedral elements of 3rd order. Such a configuration allows propagating seismic waves with a maximum reliable frequency of 1.5 Hz.

Fig. 1
figure 1

Study area: a topography model; b shear-wave velocity model; c sediment thickness model. Yellow stars indicate the epicentre (Mw 6.5 Norcia event), whereas the black rectangles define the surface fault projection

Full size image

2.2 ANN2BB: Broadband ground motions

Broadband ground motions are generated by combining the results of long-period PBSs with predictions of an Artificial Neural Network (ANN) trained on set of strong motion records. Such an approach, referred to as ANN2BB, has three main steps. First, an ANN is trained on a dataset of ground motion recordings (in our case SIMBAD v6.0, which includes also the Mw 6.5 Norcia observations, updated since Smerzini et al. 2014) to predict the short-period (\(T \le T^{*}\)) spectral ordinates based on the long-period ones (\(T > T^{*}\)); \(T^{*}\) indicates the threshold period below which ground motions from PBSs are not accurate. Second, the trained ANN is applied to estimate short-period response spectral ordinates for periods below \(T^{*}\). Third, a broadband waveform is constructed by combing the long-period PBS with a linearly scaled stochastic signal, such that the corresponding response spectrum approaches the ANN target spectrum at short periods. One of the main advantages of the ANN2BB procedure, compared to standard hybrid approaches, is its ability to simulate the specificity of the ground motion of the study area, particularly at shorter periods, and to preserve the ground motion spatial correlation properties at high frequencies. This is made possible by the correlation between short- and long-periods, as retrieved from the training dataset of earthquake recordings, on which this approach is based. The reader should refer to Paolucci et al. (2018) for further details on the ANN2BB methodology and its validation tests and to Infantino et al. (2021) for systematic analyses that demonstrate the capability of this approach to portray spatial correlation features.

2.3 Case-studies

In the present study, we investigate the 30th October 2016 Mw 6.5 Norcia earthquake simulation and ten different hypothetical scenarios obtained by varying the magnitude (from Mw 4.0 up to Mw 6.5), the kinematic slip distribution and the hypocentral location. While all the scenarios (except for the Mw4.0_S001) share the same fault geometry in the numerical model (namely a fault with a dip angle of 40° and a strike of 161°), different fault rupture scenarios are employed. A summary of the different source parameters is given in Table 1.

Table 1 Summary of the source parameters of the different simulated scenarios. For the Norcia event (first row), the source is taken from the source inversion model proposed by Pizzi et al. (2017), whereas HB94 refers to the kinematic source rupture generator of Herrero and Bernard (1994)
Full size table

Regarding the Mw6.5_S001 scenario (simulation of the Norcia event), preliminary analyses have been carried out by Özcebe et al. (2019) to test different source slip distributions from available fault inversion studies. We adopt the slip distribution (Fig. 2a) along with the fault geometry and hypocentral location proposed by Pizzi et al. (2017), as it is found to be the best performing in a comparison between observations and predictions. Other parameters, such as rupture velocity and rise time, are determined through sensitivity analyses to assess the impact of the modelling assumptions on the final outcomes. All the other scenarios (except Mw4.0_S001) assume the kinematic source model proposed by Herrero and Bernard (1994) (referred to as HB94), according to the target magnitude and fault type (Fig. 2b–d). For each HB94 source model, the rise time is randomized around a mean value of 0.5 s; however, scenarios from S002 to S008 share the same rise time field so that the hypocentral location is the only varying parameters. Figure 3 shows the slip distribution along the causative fault together with the hypocentral locations of scenarios S002-S008, whereas Fig. S1 presents the distribution of the rupture time. Such hypocentral configurations are intended to investigate rupture propagation effects on the ground motion spatial correlation. Finally, the Mw4.0_S001 scenario assumes a double-couple point-source, with a hypocentre located at the same location as scenarios Mw6.5_S001 and Mw_6.5_S002. The aim of such a configuration is two-fold: (1) to explore the dependence of the spatial correlation on the magnitude, considering a broad magnitude interval, and (2) to investigate the effect on the spatial correlation of an extended fault compared to a point source.

Fig. 2
figure 2

Slip distribution along the causative fault. a Pizzi et al. (2017); b HB94 model for the Mw 6.5 scenario; c HB94 model for the Mw 6.0 scenario; d HB94 model for the Mw 5.5 scenario. Yellow stars represent the hypocentral locations, whereas the largest rectangles indicate the maximum dimension of the fault (\(36~\;{\text{km}} \times 13~\;{\text{km}}\)). The smallest rectangles represent the ruptured faults, where the slip asperities (regions of very high slip) are concentred

Full size image
Fig. 3
figure 3

Slip distribution along the causative fault (Mw 6.5) along with the hypocentral locations of scenarios S002–S008

Full size image

3 Ground motion spatial correlation modelling

In geostatistical analysis, the most common tool adopted to represent the correlation structure between spatially distributed IMs is the experimental semivariogram, which measures the average dissimilarity of a pair of random variables separated by an inter-site distance h (e.g. Schiappapietra and Douglas 2020). The semivariogram is defined as:

$$\begin{array}{*{20}c} \hat{\gamma} \left(h \right) = ~\frac{1}{2}{\text{Var}}\left[ {\varepsilon _{{ij}} - \varepsilon _{{ik}} } \right] \\ \end{array}$$
(1)

where Var indicates the variance and \(\varepsilon _{{ij}}\) is the within-event residual representing the misfit between the observed ground motion at an individual site j (k) due to an earthquake i and the event-specific average GMM caused by path and local-site effects. In this study, we calibrate data-driven GMMs based on the simulated datasets for each ground motion component and different IMs, such as the peak ground acceleration (PGA) and 5%-damped spectral accelerations (SA) at 16 oscillator periods between 0.1 and 5 s. We perform a sensitivity test on the GMM functional form to both find the most physically representative average model and thus avoid bias. Similar analyses where carried out by Infantino et al. (2021) for the Po Plain (Italy) case-study. These authors demonstrated how the calibration of an appropriate GMM is a crucial step to both obtain robust estimates of the correlation model parameters and avoid the application of further techniques (e.g., the detrending) to get stable semivariograms. We thus adopt the following model:

$$\begin{array}{*{20}c} {\log _{{10}} \bar{Y}_{{ij}} = ~b_{1} - b_{2} \log _{{10}} \left( {R_{{line}} + b_{3} } \right) + b_{4} \log _{{10}} \left( {\frac{{V_{{s,30}} }}{{800}}} \right) + b_{5} HW~} \\ \end{array}$$
(2)

where \(b_{1} \ldots ~b_{5} ~\) are the model coefficients inferred through a one-stage non-linear regression; HW is a dummy variable introduced to specify if the site is located on the hanging wall (HW = 1) or on the footwall (HW = 0) side of the fault; Rline is the closest distance from the surface fault projection of the segment at the top edge of the rupture plan (Hashemi et al. 2015). In contrast to the standard distance metrics used for GMMs, such as the Joyner-Boore and rupture distances, we prefer using the Rline, as it is found to be more efficient (i.e. lower dispersion) in describing the near-source ground motion (e.g. Paolucci et al. 2016). We introduce the HW term to simply account for near-field effects due to both the slip distribution and directivity, which otherwise would require a more complex functional form. We assess the goodness-of-fit of the GMMs through visual inspection of the residuals, computed as the logarithm (\({\text{log}}_{{10}} )\) misfit between observations and predictions, with respect to the predictor variables and a Quantile–Quantile (QQ) plot of the residuals. An example is shown in Fig. 4.

Fig. 4
figure 4

Spectral acceleration at T = 2 s of the FP component: a Ground motion data and fitted GMMs; b residuals as a function of Rline; c QQ plot of residuals. Grey dots represent stations on the footwall for rock soil condition and the grey line indicates the corresponding GMM; Green dots represent stations on the hanging wall for rock soil condition and the green line indicates the corresponding GMM; Orange dots represent station on the hanging wall for basin soil condition and the orange line indicates the corresponding GMM. The figure shows the results obtained considering the Mw6.5_S001 scenario (30th October 2016 Norcia event)

Full size image

To assess the spatial correlation structure on the residual fields, the main steps are: (1) computing the experimental semivariogram (Eq. 1) through either the method of moments (Matheron 1962) or the estimator proposed by Cressie (1985), (2) choosing a parametric function (e.g. exponential and spherical models) to fit the sample semivariogram, and (3) estimating the parameters of the correlation models, namely the sill (i.e. the variance of the data) and the range (i.e. the distance beyond which the spatial dependency between pairs of sites is negligible) through a least-squares regression (Fig. 5). In the present study, after having shown that both the estimators provide comparable outcomes, we use the classic estimator based on the method of moments to compute the experimental semivariogram:

$$\begin{array}{*{20}c} {\hat{\gamma }\left( h \right) = ~\frac{1}{{2N\left( h \right)}}\mathop \sum \limits_{{N\left( h \right)}} \left\{ {\varepsilon _{{ij}} - \varepsilon _{{ik}} } \right\}^{2} } \\ \end{array}$$
(3)
Fig. 5
figure 5

Experimental semivariogram and corresponding exponential and spherical models: a SA (T = 1.5 s) Z component; b SA (T = 4 s) Z component. Black dots represent the experimental semivariogram estimates for each distance bin, whereas dashed lines are the fitted models. The figure shows the results obtained considering the Mw6.5_S001 scenario (30th October 2016 Norcia event). In this example, we choose the exponential model for SA (T = 1.5 s) and the spherical model for SA (T = 4 s)

Full size image

where \(\hat{\gamma }\left( h \right)\) represents the empirical semivariogram and N(h) is the number of pairs of sites with an inter-site spacing given by h. We select a maximum separation distance of 25 km and an inter-site bin width of 1 km, which results in an average value of N(h) of about 2 million in the first 10 bins and thus in well-constrained semivariances. We opt for an exponential function to model the correlation structure, as it is the most widely adopted and best performing functional form in seismology applications. However, we also implement the spherical model for some IMs because both the visual inspection of the fits and the sum of the squared errors reveals a better performance compared to the exponential model (Fig. 5b).

In most articles, it is assumed that the correlation is isotropic and hence its properties are only a function of distance and not of direction. However, this hypothesis may not always hold, and the pattern of spatial variability may vary with direction. The anisotropy can be either geometric or zonal. In the first case, the directional semivariograms feature the same sill, but different range depending on the relative orientation between pairs of sites; in the latter case, the sill varies with direction (e.g. Goovaerts 1997; Oliver and Webster 2014). Either directional semivariograms or variogram maps can be used to investigate anisotropic properties of the spatial correlation, as shown in Fig. 6. Directional semivariograms are computed for each pair of sites whose inter-site spacing falls not only in a specified distance range but also in a precise azimuth bin. We investigate common directions, such as NS and EW, and fix an azimuth tolerance of only \(10^{ \circ }\). This was made possible by the wealth of data obtained from the simulations. A variogram map (see Fig. 6b) displays the semivariance contribution of each pair considering simultaneously all distance and azimuth bins. Concentric contour plots imply an isotropic variation, whereas patchier distributions reflect anisotropic patterns in correlation. Any cross section of the map corresponds to the more familiar one-dimensional semivariogram. Alternatively, nonparametric tests (e.g. Garakaninezhad and Bastami 2017; Huang et al. 2020) can be employed to quantitatively assess anisotropy.

Fig. 6
figure 6

a directional semivariograms computed for different directions: 0—NS, 45—NE–SW, 71—FN, 90—EW, 135—NW–SE, 161—FP; b Variogram map. The black dashed arrow indicates the NS direction. The figure shows the results obtained considering the Mw6.5_S001 scenario (30th October 2016 Norcia event)

Full size image

Furthermore, the hypothesis of stationarity may not be valid due to specific source and path effects, as suggested by Chen and Baker (2019) and Infantino et al. (2021). In such situations, the semivariogram tends to increase indefinitely without levelling off at a constant sill value and the random variables (e.g. within-event residuals) exhibit a gradual variation in space (Fig. 7a) that masks potential small-range correlation structure. Trend surface models are commonly adopted to model spatial trends and thus remove large-scale correlation patterns, leading to a patchier distribution of the random variable (Fig. 7b) (Oliver and Webster 2014). We implement such an approach in all those cases where the GMM is not able to sufficiently describe the ground motion median behaviour and capture specific features, such as rupture propagation and path effects. Alternatively, nonparametric isotropic GMMs calibrated as a function of few explanatory variables by using other regression techniques, such as LOESS (locally estimated scatterplot smoothing), could be used to potentially avoid this problem.

Fig. 7
figure 7

Spatial variation of within-event residuals of SA (FP) at T = 4 s: a raw data showing a gradual variation of the residual values; b detrended data featuring a patchier distribution. Yellow star indicates the epicentre (Mw 6.5 Norcia event), whereas the grey and black rectangles are the surface fault projection and the effective surface fault projection, respectively. The figure shows the results obtained considering the Mw6.5_S001 scenario (30th October 2016 Norcia event)

Full size image

4 Results

4.1 Mw 6.5 Norcia earthquake simulation

4.1.1 Comparison with recordings

The 30th October 2016 Mw 6.5 Norcia earthquake was recorded by more than 100 stations, belonging to both permanent and temporary seismic networks, within an epicentral distance of 200 km (Luzi et al. 2019). The uniqueness of this dataset lies on the availability of 36 near-source recordings at epicentral distances less than 30 km (Fig. 8d). We compute experimental semivariograms using the data from both simulations and observations and compare them to assess the capability of 3D PBSs and ANN2BB to generate spatially correlated ground motion fields accounting for the actual correlation structure. Recordings and station-metadata are from the Engineering Strong Motion database (ESM). Infantino et al. (2021) perform similar comparisons for the Po Plain (Northern Italy) case study, finding a good agreement between sample semivariograms obtained from observations and simulations over a broad range of periods. As shown in Fig. 8a–c, the Norcia case-study does not show such satisfactory agreement. We propose three possible reasons for this. First, the numerical model does not describe all the small-scale irregularities of the geo-tectonic structure, making the ground motion prone to be less variable. Second, 34 out of 36 location selected in the numerical model have a constant Vs30 equal to 1700 m/s, whereas the ESM stations feature different Vs30 with an average of about 650 m/s (Fig. 8d); most of the simulated data are thus located on homogeneous hard rock that undeniably makes the ground motion more correlated. Third, source models are retrieved through finite-fault inversions and are usually calibrated on very low frequency ranges (e.g. Pizzi et al. 2017). As a consequence, source models lack intrinsic complexity that is inherent in the real world and, in turn, the resulting ground motion features a less variability, affecting both the sill and range. Nonetheless, we note that our results show a realistic trend of the semivariogram, as the semivariances increase with increasing separation distances until they level off at a constant sill value. Therefore, such comparison supports the ability of 3D PBS along with the ANN2BB approach to reproduce the ground motion spatial correlation structure, as already corroborated by systematic analyses reported in Infantino et al. (2021).

Fig. 8
figure 8

a Experimental semivariograms obtained by using the ANN2BB approach (Predictions) and observed recordings for PGA; b experimental semivariograms for SA (T = 2 s); c experimental semivariograms for SA (T = 5 s); d spatial distribution of the seismic stations (epicentral distance < 30 km) that recorded the Norcia event. Dots are color-coded based on the Vs30 values. The red star is the epicentre, whereas the black rectangle represents the projected fault surface (data are from https://esm-db.eu/#/home)

Full size image

4.1.2 Ground motion directionality

In the present study, in addition to the geoH horizontal component, we also present results for other component to identify diagnostic spatial correlation features. Figure 9 illustrates the range and the sill as a function of the oscillator period for the different ground motion components. First, we find that the spatial correlation structure in terms of the range is generally proportional to the considered period, as previously observed (e.g. Schiappapietra and Douglas 2020). This applies to the FN and Z components, whereas the trend is less evident for the FP and geoH ones. Besides, our results show that the correlation between range and period is not well defined at shorter periods (T < 0.5 s), as found in other studies, such as Esposito and Iervolino (2012) and Wagener et al. (2016). Figure 9b suggests that the sill is similarly affected by the vibration period. This result is noteworthy, as it is common practice to work with normalized residuals and therefore the sill is not estimated, being equal to 1. Similar outcomes are provided in Sgobba et al. (2019, 2020), who estimated the range and sill of the source-, path- and site-corrective terms of the ground motion model specific for the Po Plain and central Italy regions, respectively. Secondly, the FN sill and range values tend to be larger than the FP ones over a broad range of periods, in agreement with Infantino et al. (2021), who investigated the FN/FP ratios for 6 different 3D PBSs. This is related to the fact that the FN component is typically strongly affected by directivity effects, which cause the ground motion to be more coherent and thus correlated over longer distances compared to the FP. Indeed, the normal fault mechanism along with the slip distribution, which is characterized by a slip asperity (regions of very high slip) close to the top edge of the fault (Fig. 2a), causes a focusing of the seismic energy from the propagating rupture front along the up-dip direction. Besides, the differences in terms of range and sill rise with increasing period (T > 2.5 s) as a consequence of directivity effects, being predominant at longer periods. The same applies to the sill, which is strongly influenced by the slip asperities. Likewise, the vertical component shows remarkable directivity effects due to the focal mechanism, which is normal faulting with a dip of 40°. The Z component is indeed characterized by larger range and sill values across almost all periods. To better explain these outcomes, we show the ground motion maps for SA (T = 3 s) in Fig. 10. Not only does the vertical component feature homogeneous maximum peak values distributed over a more extended area, but also higher variability in terms of peak values. As a consequence, the resulting ground motion is correlated over longer distances (larger range values) and is characterized by a larger sill with respect to the other components. Finally, it is noted that the spherical model provides a better performance at long periods (T = 4 and 5 s) for all the components; this leads to slightly smaller ranges compared to the exponential functional form.

Fig. 9
figure 9

a Range as a function of the period T for different ground motion components; b sill as a function of the period T for different ground motion components

Full size image
Fig. 10
figure 10

Ground motion maps for SA (T = 3 s): a geometric mean component; b FN component; c vertical component; and d FP component

Full size image

4.1.3 Spatial correlation anisotropic properties

We relax herein the assumption of isotropy and we compute directional semivariograms for the following azimuths: (1) 0° (North); (2) 45° (North–East); (3) 71° (FN—normal to the fault strike); (4) 90° (East); (5) 135° (South–East); (6) 161° (FP—parallel to the fault strike). It is recalled that directions between 180° and 360° provide the same results because of the symmetric property of the semivariogram (Webster and Oliver 2007). Figures 11 and 12 present the range and sill, respectively, as a function of period in terms of average values computed over the different directions along with their standard deviations. There is considerable variability across all periods in terms of both sill and range, meaning that the hypothesis of isotropy is not suitable for any ground-motion component. We also show the trends in the FN and FP directions, highlighting how the former represents a rough lower bound, whereas the latter constitutes an upper bound. This is a rather remarkable but expected result. While the FN direction is mainly affected by the faulting mechanism, rupture directionality effects have a strong impact on the FP direction, leading to more coherent (larger range) and more variable (higher sill) ground motions. Such an observation is also made by Sgobba et al. (2020). While applying their novel methodology to produce non-ergodic shaking scenarios for the Mw6.5 Norcia case-study, the authors identify a strong azimuthal dependence due to rupture directivity along the strike direction. This is likely connected to the main tectonic features of the Apennine region, where faults mostly follow a NW–SE trend. Finally, the FN over FP range ratio shows that on average the FN component is correlated over longer distances compared to the FP one due to strong directivity effects, especially at longer periods, as found for the isotropic case (Fig. 9).

Fig. 11
figure 11

Average range values, computed in the different directions, as a function of the period T. a Geometric mean component; b vertical component; and c FN over FP components ratio. The grey area represents the mean\(\pm ~\)standard deviation. The FN-direction and FP-direction range values as a function of T are also reported on the graphs

Full size image
Fig. 12
figure 12

Same as in Fig. 11 but in terms of sill values, computed in the different directions, as a function of the period T

Full size image

Finally, for the sake of completeness, we present in Fig. 13 the experimental semivariograms and the corresponding models obtained along the FN and FP directions for SA (T = 3 s). Clearly, the semivariogram in the FP direction has a larger sill and range compared to the one in the FN direction.

Fig. 13
figure 13

Directional semivariograms for SA (T = 3 s) for the geometric mean component. Dots and squares represent the experimental semivariograms computed considering azimuths of 71° (FN) and 161° (FP), respectively. Solid lines represent the corresponding models

Full size image

4.2 Dependence of spatial correlation on source effects

4.2.1 Earthquake magnitude

The relationship between magnitude and range has been extensively studied by several authors but it is still under debate (Schiappapietra and Douglas 2020). Indeed, the database heterogeneity in terms of, for example, fault mechanism and geometry, stress drop as well as regional and local-site conditions, may contribute to the variability in the range in addition to the effect of magnitude. To deepen our knowledge on this topic, we carry out different 3D PBSs by varying the magnitude while keeping the same causative fault. Although a clearer dependency of the range on the magnitude is evident when larger Mw differences are considered (e.g. Mw 6.5 Vs. Mw 5.5–4.0), Fig. 14 suggests that there is not a unique and well-defined trend between magnitude and range for any component and therefore other factors, such as the rupture process, should be considered to explain the range variability. While larger events should feature larger correlation lengths because of their lower frequency energy content, we believe that this is true only in the far-field where the point-source assumption can be deemed valid. In the near-field, the effect of the fault extension along with the intrinsic variability of the rupture mechanism are found to play a crucial role in determining the correlation. A more heterogeneous slip distribution on a larger fault may reduce the coherency of the ground motion, leading to smaller range values. At the same time, more homogeneous slip asperities on the fault plane may induce a ground motion correlated over longer distances. Such assumptions could explain the trend of the Mw 4.0 scenario; although its range values are relatively small, it provides correlation lengths as large as those of the higher-magnitude scenarios. Similar thoughts can be found in Stafford et al. (2018). Indeed, while investigating the impact of the rupture process on spatial correlations using finite difference simulations, Stafford et al. (2018) found a negative correlation between magnitude and range, with Mw 3.0 scenarios having on average a larger range compared to the Mw 6.0 ones. Besides the distribution of the slip asperities on the fault, rupture propagation phenomena coupled with the morphology of the basin as well as the topography may give rise to a higher range variability, masking the real dependency of spatial correlations on magnitude.

Fig. 14
figure 14

Range as a function of the period T for different Mw scenarios: a geometric mean component; b FN component; c vertical component; and d FP components

Full size image

The sill seems to be correlated to both the slip asperities, which contribute to the intrinsic variability, and the relative position of such asperities with respect to the hypocentre. In Fig. 15, we observe that the Mw6.5_S001 scenario generally gives the highest sill values across all periods and for any component. We do not find any particular trends with magnitude for the geoH and FP components, where the sill values are rather comparable across all the scenarios. Conversely, we note some magnitude dependency for the Z and FN components, for which the fault mechanism and directivity effects, in addition to the magnitude, play a significant role in determining the variability of the ground motion. Finally, we recall that the slip distributions of Mw6.5_S002, Mw6.0_S001, Mw5.5_S001 and Mw4.0_S001 scenarios stem from the rupture generator by Herrero and Bernard (1994), whereas the source model of Pizzi et al. (2017) was used for the Mw6.5_S001 scenario. This may contribute to the similarity in terms of sill values of the former.

Fig. 15
figure 15

Sill as a function of the period T for different Mw scenarios: a geometric mean component; b FN component; c vertical component; and d FP components

Full size image

4.2.2 Slip distribution

We examine herein the role of the slip distribution by considering two ground shaking scenarios which, while having the same magnitude, hypocentre and causative fault, have different source models (Mw6.5_S001-S002). The impact of the source model is clearly evident in Fig. 16, in which the maps of ground shaking are presented for SA(T = 2 s) and for the Z and FN components. In scenario S001, the slip distribution has a large, more homogeneous slip asperity close to the top edge of the fault, which is located along the path from the hypocentre towards the footwall side. Large peak values are thus generated at all sites located in the up-dip projection of the fault (Fig. 16a, c), leading to more coherent ground motions. This is further highlighted by the range and sill ratios computed as S001/S002 and presented in Fig. 17. In general, scenario S001 features ground motions correlated over longer distances and with a higher variability over a broad period range for all ground-motion components, except for FN, with respect to scenario S002. The different behaviour of the FN component is evident from Fig. 16b. The S002 scenario is characterized by a bilateral rupture, which tends to enlarge the area characterized by more homogeneous higher ground motion amplitudes. Therefore, the ground motion has a correlation structure with a larger correlation length. Our outcomes are consistent with Stafford et al. (2018), who demonstrated how the rupture process of scenarios with equal magnitudes have a pronounced impact on the range variability. Similarly, Chen and Baker (2019) and Infantino et al. (2021) identified different spatial patterns of the correlation coefficient exclusively because of slip distribution and source propagation effects.

Fig. 16
figure 16

SA (T = 2 s) Ground motion maps for Mw6.5_S001 (left panel) and Mw6.5_S002 (right panel) scenarios: a, b FN component; and c, d vertical component

Full size image
Fig. 17
figure 17

Ratio between Mw6.5_S001 and Mw6.5_S002: a range values; and b sill values

Full size image

4.2.3 Hypocentral locations

The relative position between slip asperities and the hypocentre is a key element that has a strong influence on the spatial correlation structure of earthquake ground motions. Here, we address the role of the hypocentral location by considering scenarios S002–S008, which differ solely in terms of their nucleation points. Figure 18 shows that we cannot identify a unique correlation trend between the FN and FP components. The lack of such tendency is attributable to the relative position between the slip asperity and the hypocentre which determines the size of the directivity effects. For instance, in scenarios S004, S005, S007 and S008 the path from the nucleation point to the main slip asperity follows a fault-parallel direction, causing a polarization of the FP ground motion, compared to the FN. As a result, the latter shows a correlation structure with a smaller correlation length across almost all periods. The S006 hypocentre is located close to that of scenario S002 and similarly it shows a significant directivity for the FN component. At the same time, rupture propagation effects along the FP components are marked. The combination of these effects leads to a similar correlation structure of the FN and FP in terms of range values. Finally, the S003 hypocentre is symmetrical to that of scenario S002 with respect to the main slip asperity; therefore, the rupture propagates in the opposite direction (i.e. towards the asperity) causing considerable “backward” directivity effects and leading to a correlated FN component over longer distances compared to the FP.

Fig. 18
figure 18

Ratio of FN/FP range for the different scenarios with varying hypocentral location

Full size image

We further test the effects of the hypocentre location on spatial correlation by looking at possible anisotropy patterns. Figure 19a, b compare the average range and sill values computed for the various scenarios for each azimuthal direction, respectively. For the sake of clarity, we plot on a different graph (Fig. 19c, d) the standard deviations of the range and sill values for each considered direction. Four main observations can be highlighted. First, the average range and sill values tend to increase with increasing period, independently of the azimuth. Second, the range and sill in the FP direction represent an upper bound, whereas those in the FN direction constitute a lower bound; rupture propagation effects along the FP direction prevail over directivity effects along the FN direction, thus leading to patterns of ground motion spatial variability with preferential direction along the strike of the fault. Such a phenomenon is evident in Fig. S2, which shows the ground motion shaking of the spectral acceleration (geoH) at T = 2 s for each scenario. Similar outcomes were found by Garakaninezhad and Bastami (2017) especially for strike-slip mechanisms. Third, there is higher variability in terms of both range and sill along the FP direction compared to the FN one. While the latter is mostly influenced by the focal mechanism, which is the same for all the scenarios, the former is strongly sensitive to both the rupture propagation and hypocentral location, which vary among the case-studies. As a result, the FP direction, besides having larger range and sill values, features also a larger variability due to the rupture process. Fourth, the variability across all scenarios both in terms of range and sill tends to increase with increasing periods, meaning that the impact of rupture propagation phenomena on spatial correlations is stronger at longer periods. These results refer to the geometric mean component; however, similar outcomes are obtained for the other ground-motion components. The full set of figures is provided in the supplementary material (Figs. S3, S4 and S5).

Fig. 19
figure 19

a Average and c standard deviation range values computed for scenarios Mw6.5_S001-S008 for the different azimuth directions; b average and d standard deviation sill values computed for scenarios Mw6.5_S001-S008 for the different azimuth directions

Full size image

4.2.4 Finite fault versus point-source

We mentioned in Sect. 4.2.1 that the effect of a finite fault can be significant in defining the correlation structure in the near-field. Here, we explore spatial correlation patterns caused by a point-source. Because of the spherical propagation from the nucleation point, we would expect a more isotropic ground motion field. However, Fig. 20 shows significant spatial anisotropies in the correlation of the Mw4.0_S001 scenario, especially for the vertical component. Similarly to Figs. 11 and 12, Fig. 20 presents the range and sill as a function of the period in terms of average values computed for the different directions along with their standard deviations. We believe that such anisotropic effects are likely caused by the radiation pattern, which may exhibit a distorted four-lobed pattern due to propagation in the heterogenous medium. When dealing with finite faults, this effect is also coupled with the rupture propagation on the fault plane; therefore, considering an isotropic, rather than an anisotropic, spatial correlation model may be a major simplification.

Fig. 20
figure 20

Average range (a) and sill (b) values computed on the different azimuth directions for the Mw 4.0 point-source scenario. The shadow areas represent the mean\(\pm\)standard deviation

Full size image

Furthermore, ground motion shaking maps (Fig. S6) suggest that topographic amplifications may significantly contribute to spatial anisotropy patterns in addition to the radiation pattern. Topographic effects are indeed not negligible in the numerical model (Fig. 1a). Finally, the sill shows a less pronounced variability, especially for the geoH component (Fig. 20b). This is reasonable since the sill seems to be significantly coupled with the slip asperities, that contribute to the intrinsic variability of the ground motion. In this case-study, the slip is concentrated at a source-point and therefore does not feature the inherent heterogeneity of the finite fault.

5 Conclusions

In this study, we explored the spatial correlation structure of response spectral accelerations from a set of broadband physics-based ground motion simulations generated for the Norcia (Central Italy) area. We use classic geostatistical tools, such as the semivariogram, to evaluate properties of the ground motion spatial correlation under both the assumptions of isotropy and anisotropy with a level of detail which could not be achieved by using recordings. Indeed, semivariance estimates are well-constrained despite the relatively small bin-width and azimuth tolerance used in computing the semivariograms.

It is widely recognized in literature that a positive correlation exists between range and period of interest. Not only are our results in agreement with such statement, but we also demonstrate that the sill also tends to increase as the period increases. This result is rather interesting, as it is common practice to work with normalized residuals so that the sill is not directly estimated.

In the near-source region, the polarization of the ground motion can be significant with larger FN and Z peak values due to directivity effects. We, therefore, investigated the spatial correlation structure of different ground motion components to identify diagnostic features. The specific case of the Mw 6.5 Norcia event simulation (scenario Mw6.5_S001) presents a FN ground motion with a larger intrinsic variability and correlated over longer distances compared to the FP component, as a result of strong directivity effects. The slip distribution coupled with the normal faulting mechanism also significantly affects the Z component, which consequently shows the largest range and sill values over a broad period range. At the same time, the analysis of possible spatial anisotropy patterns reveals that the ground motion field has a strong azimuthal dependence due to rupture propagation effects along the strike direction (FP). This result is consistent with the tectonic setting of the region, as also demonstrated by Sgobba et al. (2020).

The availability of different rupture scenarios generated for the same causative fault allowed the investigation of several aspects of the spatial correlation, such as the dependence on the magnitude, slip distribution and hypocentral location. We believe that the magnitude itself cannot explain the large variability of correlation lengths among different events, especially when the same area is considered. As a matter of fact, Heresi and Miranda (2019) found that only a small ratio of the range variability can be ascribed to magnitude. Our results suggest that the rupture process, both in terms of slip distribution and hypocentral location, has a strong contribution to determine the correlation structure of ground motion IMs, in agreement with the findings of Stafford et al. (2018).

Simultaneously, we observed that the relative position between the hypocentre and the main slip asperity has a strong impact on anisotropy patterns. Not only does the FP direction show on average the largest range and sill values, but it is also characterized by a larger variance among the different scenarios (S002-S008) owing to the different rupture propagation phenomena. Conversely, the FN direction shows rather similar spatial patterns among the case-studies, being mostly affected by the faulting mechanism. Similarly, Chen and Baker (2019) and Infantino et al. (2021) suggested that non-stationarity and anisotropy in spatial correlation strongly depend on the source rupture process.

Although the comparison with recordings shows some discrepancies due to the simplifications of the numerical model, this work offers valuable insights into the spatial correlation of ground motions. Such results would likely be challenging to reach with earthquake recordings due to the shortage of data, especially in the near-source region of major earthquakes. Our outcomes suggest that the spatial correlation structure of ground motion IMs is not only period-dependent, but also scenario-dependent, so that more care should be taken when pooling data from different earthquake to calibrate a unique correlation model. Consistently with other studies (e.g. Chen and Baker 2019; Huang et al. 2020; Infantino et al. 2021), our results strengthened the idea that the isotropy assumption may be a strong simplification and thus not reasonable for the seismic risk assessment of spatially-distributed infrastructure.

Finally, we can state that 3D PBSs represent a powerful tool that provide databases with an unparalleled size and richness, which allows specific features of the spatial correlation structure to be addressed. This is particularly important for those regions characterized by sparse seismic networks, for which developing a well-constrained correlation model is challenging. Further research should be undertaken to explore if the correlation properties identified in this work have a significant impact on the regional seismic risk assessment of portfolios of buildings, infrastructures and earthquake-induced phenomena.