1 Introduction

Quantifying the potential level of ground shaking for a given site or an area allows for an assessment of the level of preparedness and of the economic potential required for proper earthquake protection. This is especially true for many large agglomerations worldwide which are frequently located over extended and often deep sedimentary basins. Several recent investigations have highlighted that thick and soft sediments can strongly amplify short but also long-period ground-motion (e.g., Joyner 2000; Koketsu and Miyake 2008; Denolle et al. 2014; Mascandola et al. 2017).

The simulation of broad-band ground-shaking over spatially extended basins with sharp transitions and laterally variable sedimentary layers at regional scales is, however, challenging. Appropriate regional 3D physics-based simulations are usually limited to low frequencies (up to 1 to 2 Hz) while classical empirical ground-motions models, on the other hand, do not reproduce site-specific geological conditions and rupture details of each earthquake. For most empirical ground-motion models, site effects are generally taken into account through vS30 only, the travel-time based average S wave velocity in the uppermost 30 m. Correspondingly, the thickness of deep sedimentary basins and its impact at long period ground-motion are not considered appropriately by classical empirical models used in engineering seismology, with the notable exceptions of the recent NGA-West ground-motion models (Bozorgnia et al. 2014) which incorporate a factor depending on the depth at which the S wave velocity is exceeding a given threshold value. Moreover, sophisticated approaches have been developed for considering the response of the entire sedimentary column (e.g. Bazzurro and Cornell 2004; Rodriguez-Marek et al. 2014). In these models, the shaking for reference rock conditions, i.e. a hard-rock horizon with vS much larger than 800 m/s, is computed and convolved with 1D modelling results. This approach, however, is difficult to apply at regional scales due to the following reasons: (1) ground motion prediction equations (GMPEs) are well calibrated for soft rock (with vS30 up to 800 m/s) but not for harder rock, (2) vS30-κ adjustments (from soft to hard rock) are still not understood completely (herein, κ represents the empirical high-frequency spectral decay of the acceleration spectra, Anderson and Hough 1984), (3) it is not clear which depth is necessary to reach the main impedance contrast and the true “bedrock” (i.e. a homogeneous half-space free of site effects), (4) 1D models are usually well calibrated only at shallow depths and (5) variations of ground-motion are influenced not only by the local 1D site conditions but also by the 3D environment such as topography, bedrock slope as well as corresponding wave conversion effects at basin edges.

The influence of thick sedimentary layers and the associated long-period amplification effects discussed here are relevant to the Lower Rhine Embayment (LRE) in western Germany. In general, the seismicity in the region is indeed low with respect to plate-boundary regions of the Mediterranean but it is remarkably elevated along the course of the Rhine River up to the Netherlands and into the adjoining parts of Belgium with respect to Central Europe. The LRE forms the southernmost part of the Dutch-German rift structure with extensional tectonics and a set of normal faults in a horst and graben structure (Camelbeeck et al. 2007). Although faults in the LRE have rather low slip rates of less than 0.1 mm per year, the area produces the highest seismic hazard in Germany. The LRE was subject of paleo-seismological investigations during the last decades indicating that their recent activity remains difficult to constrain (Vanneste et al. 2013). Historical records of reports of seismicity reach back hundreds of years and numerous historical events were derived by analyses of written sources (Ahorner 1983; Leydecker 1986, 1999; Reamer and Hinzen 2004; Hinzen and Reamer 2007). The strongest historical earthquake in the area was the Düren earthquake of 1756 (moment magnitude Mw 5.8, Meidow 1995; Grünthal and Wahlström 2003). The more recent 1992 ML 5.9, MW 5.4 Roermond earthquake, located in the Province of Limburg in the south-eastern part of the Netherlands, can be considered the strongest instrumentally recorded event in the area (Pelzing 1996).

Adding to the shaking susceptibility in this region is the fact that in the LRE, the shallow subsurface structure consists mostly of soft sediments of Tertiary and Quaternary age with significant lateral variations of thickness overlying the Devonian bedrock, thus producing significant frequency-dependent modifications of ground-motion. In the past, large-scale investigations of local site responses were already carried out based on measurements of seismic noise (Parolai et al. 2001, 2002; Scherbaum et al. 2003) and numerical simulations (Weber 2007).

The aim of the present paper is to quantify the shaking that may be produced by a large earthquake in this area (i.e. a deterministic scenario) taking into account the influence of thick sedimentary layers on ground-motion for the southern LRE. The selection of a deterministic scenario is predicated on planning efforts for emergency response and earthquake losses. A good knowledge of the LRE basin properties and the availability of several moderate earthquakes time histories recorded by a relatively dense regional seismic network allow a comparison of different methods and inherent uncertainties for scenario simulations of ground-motion. To this regard, we first develop a harmonized 3D model of the sedimentary cover derived from geology, seismic experiments and borehole information. As shown in Fig. 1 and as outlined in the following sections, we implement three alternative approaches to compute ground-motions accounting for the influence of the thick sedimentary cover. In a first step, we select and test different ground-motion models in which the influence of the sedimentary cover is taken into account empirically. Secondly, from the 3D basin model, we compute 1D amplification functions which allow for the adjustment of rock response spectra through Random Vibration Theory (RVT, Cartwright and Longuet-Higgins 1956) and Inverse Random Vibration Theory (IRVT, Vanmarcke and Gasparini 1976) approaches. Thirdly, hybrid physics-based ground motion simulations are used to predict time histories for soft rock conditions which are subsequently adjusted using the 1D amplification functions calculated above. We compare and discuss differences and similarities of all three procedures.

Fig. 1
figure 1

Overview of the methodologies used in this study for obtaining broad-band and site-specific ground-motion intensity measures. See a detailed description including a definition of parameters in the following

Full size image

2 Development of a 3D velocity and attenuation model of the Lower Rhine Embayment

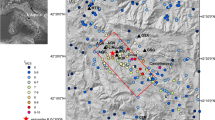
For constraining the 3D geometry and crustal structure of the LRE, Breddin (1954) created a series of high-resolution hydrogeological maps, mainly for assessing the impact of the planned open coal pits in the region. Weber (2007) collected numerous ground water table data, information on deep boreholes and a large number of geological cross sections. The drillings extend several 100 m in depth, often reaching the sediment-bedrock interface. Even for the western LRE, where the thickness of the sedimentary cover can be up to 1350 m, some of the boreholes reach the bedrock. Additional geological and stratigraphic information from the database of the Geological Survey of North Rhine-Westphalia was incorporated (Hilden 1988a, b; Knapp 1988; Knauff 1988). In the end, the final structural model is based on 670 sites on a 2 km grid (Fig. 2). For each site, a 1D stratigraphic profile is available. As outlined by Weber (2007), for many of those sites, remarkable stratigraphic contrasts with several softer coal layers at various depths between stiffer layers are present.

Fig. 2
figure 2

Seismo-tectonic framework of the LRE. Black lines represent seismic faults (Vanneste et al. 2013). The black dots indicate positions of the 1D velocity-depth and density-depth profiles. White triangles in the north-eastern part of the map in the Cologne area represent measurements of seismic noise by Parolai et al. (2001, 2002). Maroon colours represent inhabited areas. The red dashed lines indicate the location of the velocity cross sections shown in Fig. 3. The yellow star indicates the epicentral location of the scenario event. Sites S116 and S445 are used as a case study in the following figures

Full size image

Budny (1984), using a large number of downhole measurements in the LRE, established generalized velocity-depth and density-depth relationships for different soft geological materials occurring in the LRE (soft coal, clay, gravel, sand, schist, silt, tuff). Additionally, seismic velocities and information on density had been derived by Budny (1984) for various hard-rock formations (marlstone, sandstone, mudstone, argillite). Since only limited velocity information was available for marlstone, the velocity-depth relationship of sandstone was used for marlstone since the marlstone velocity values were within the residuals of the sandstone values. For establishing density-depth relationships for marlstone and sandstone, information from literature taken from the Upper Rhine Graben (Brüstle and Stange 1999) has been used. Weber (2007) quantifies the quality of the empirical velocity-depth and density-depth relationships concluding that the depth dependency of the S wave velocity is well represented for most materials on the LRE. While the relationships for clay and schist are of moderate quality, significant uncertainties exist only for silt and tuff.

In a similar manner, Budny (1984) determined material-specific depth-dependent quality factors for S waves (QS). Due to the limited amount of data, material-specific values are generally characterized by a large scatter, meaning that the fit is not well constrained. For the development of the 3D model on QS and for further constraining the measurements, we follow Budny (1984) proposing the use of low values for QS (QS ≤ 10) only for the very shallow layers (< 10 m) while for deeper layers (> 100 m), QS values larger than 20 are used. Using the available velocity-depth, density-depth and QS-depth relationships for different geological materials, a 3D model for vS, vP, density and QS has been derived by interpolating all available site-specific information.

In addition to the data sets derived on the regional scale, Parolai et al. (2001, 2002) carried out seismic noise measurements at more than 200 sites in the north-eastern part of the LRE with a spatial focus on and around the city of Cologne (measurement sites are indicated in Fig. 2). Inverting the individual horizontal-to-vertical spectral ratios obtained from seismic noise measurements, for each site a 1D S wave velocity profile was derived (Parolai et al. 2006). Weber (2007) showed a good agreement of their results with the results of Budny (1984) in the overlapping area. For the municipal area of Cologne, however, seismic noise measurements allow a much higher spatial resolution of the resulting velocity model.

3 Computation of site response

As shown in Fig. 3, the thickness of the sedimentary cover generally increases from a few meters at the north-eastern suburbs of Cologne where the Devonian basement rocks outcrop in the mountainous area of the ‘Bergisches Land’, to more than 1000 m west of the Erft fault system (for example, see the drastic increase in thickness for the central part of the northernmost cross section in Fig. 3). Due to the flat topographic relief across the LRE it is expected that topographic site effects can be neglected. Richwalski et al. (2006) further indicate that a large part of the area can well be described assuming 1D resonance effects only, although 2D and 3D effects cannot fully be excluded as shown by Ewald et al. (2006) who carried out low-frequency ground-motion simulations in the LRE. Therefore, based on the 1D assumption as an acceptable working hypothesis, we will apply 1D analysis for calculating theoretical amplification functions from available velocity and attenuation data sets.

Fig. 3
figure 3

S wave velocity cross sections through the LRE. The location of the cross sections is indicated in Fig. 2

Full size image

For this, we follow the classical Knopoff layer matrix description (Knopoff 1964). For each site for which site-specific velocity, density and attenuation profiles are available, we calculate complex amplification functions with respect to soft rock conditions, i.e. with respect to a reference velocity of vS30 = 760 m/s (National Earthquake Hazards Reduction Program NEHRP site condition B/C, a reason for applying this value is given below in Sect. 5). Since the deep velocity structure will affect the amplification spectra both in the low and in the high-frequency range, this means that the amplification function with respect to soft rock conditions is calculated by dividing the amplification function for the full profile by the amplification of a profile all the way down starting at a depth at which vS exceeds 760 m/s. An example is shown in Fig. 4. As indicated in Fig. 2, amplification functions are calculated for approximately 870 sites. Ground-motion at the investigated sample site in eastern Cologne is amplified over a wide frequency range between 0.5 and 5 Hz with a maximum amplification due to the resonance occurring around 0.6 Hz. In the high-frequency range (f > 5 Hz), ground-motion is significantly attenuated due to the low quality factors in the shallow sedimentary layers.

Fig. 4
figure 4

Left: P wave (dashed line), S wave velocity (solid line) and density model (dotted line) for site S116 in Cologne-Deutz (50.93° N, 7.01° E, see Fig. 2). Right: Complex 1D SH amplification function (vertical incidence) with real (dotted line), imaginary (dashed line) and absolute value (solid black line) with respect to a soft rock reference velocity of vS30 = 760 m/s (see text for further details)

Full size image

4 Testing and selection of GMPEs and empirical ground-motion modelling (method 1)

A review and comparison of an initial list of GMPEs was carried out to identify a final set of suitable candidate empirical ground-motion models for the target region based on the recommendations by Cotton et al. (2006) and Bommer et al. (2010). The selection of GMPEs was mainly driven by the availability of suitable metadata in the target region and the ability of the selected GMPEs to take into account the influence of site effects not only by vS30. Finally, four different ground-motions scaling relations for active shallow crustal earthquakes are selected (characterizing the target area as a stable continental region would be a too severe simplification, Grünthal et al. 2018). We encounter the application of the equations of Abrahamson et al. (2014, ASK14), Boore et al. (2014, BSSA14), Campbell and Bozorgnia (2014, CB14) and Chiou and Youngs (2014, CY14) of the recent NGA-West 2 project (Bozorgnia et al. 2014). To our knowledge, these equations (and the corresponding previous NGA-West 1 models) are the only ones which account for additional factors like sediment thickness for characterizing basin effects not fully captured by vS30.

For the evaluation, we follow the proposal by Scherbaum et al. (2004) and we apply a dataset of 16 weak and moderate earthquakes (3.1 ≤ M ≤ 4.4) which occurred in and around the LRE since January 2007 and which were recorded by at least three stations. For network stations in the LRE, vS30 and z1 for the equations of Abrahamson et al. (2014), Boore et al. (2014) and Chiou and Youngs (2014) are taken from the 3D model described above. Herein, z1 represents the depth at which vS exceeds 1 km/s. vS30 ranges between 150 m/s and 730 m/s and z1 ranges between 0.16 km and 1.30 km. Similarly, Campbell and Bozorgnia (2014) use a parameterization with vS30 and z2.5 (the latter describes the depth at which vS exceeds 2.5 km/s). For stations outside the LRE, vS30 and z1 or z2.5 are assessed using large-scale geological models of the area (Geological Survey of Belgium 2010; Geological Survey of North Rhine-Westphalia 2013, 2016; State Office for Mining and Geology Rhineland-Palatinate 2016). We applied similar correlations between geology and seismic velocities as described in the previous section. For four stations outside the LRE, z1 or z2.5 could not be assessed; the values were therefore set to the recommended default values given for each GMPE (δz1 = 0.0481 km for ASK14, δz1 = 0.0 km for BSSA14, δz1 = 0.0413 km for CY14, δz2.5 = 0.6068 km for CB14). Moment magnitudes for the selected events (the magnitude scale used by the selected GMPEs) are taken from the European-Mediterranean Earthquake Catalogue (EMEC, Grünthal and Wahlström 2012) with its temporal extension as described in Stromeyer and Grünthal (2015). Using the geometrical mean between the two horizontal components, response spectra with 5% damping have been calculated considering the limits of the individual ground-motion models. Figure 5 compares observations and ground-motion modelling results for peak ground acceleration (PGA) and spectral acceleration SA at a period of T = 1 s.

Fig. 5
figure 5

Response-spectra residuals using different NGA West 2 ground-motion models (Abrahamson et al. 2014, top, Boore et al. 2014, second from top, and Campbell and Bozorgnia 2014, second from bottom, and Chiou and Youngs 2014, bottom) for PGA (left) and SA (T = 1 s, right) compared to a Gaussian distribution with unit variance (black line)

Full size image

The central tendency is underestimated, meaning that all models more or less underpredict the level of ground-motion in the area. Such bias might be caused by (1) differences between various Mw magnitude scales or variations of the magnitude scaling in the ground-motion models which are not closely accounted for, (2) regional differences in stress drop, and (3) an insufficient consideration of site effects due to the thick sedimentary cover. With regard to (2), stress drop analyses of events close to the target area have shown larger stress drop values compared to the average observed in active parts of Europe (Scherbaum et al. 2004) while other studies suggested lower stress values for this area (De Crook 1989). With regard to (3), several stations (e.g. network sites Grosshau GSH and Dreilaegerbach DREG of the German Regional Seismic Network) are located on thick layers of sediments particularly affecting ground-motion at longer periods. For these stations, seismic velocities of the sedimentary cover could only be assessed based on large-scale geological models and based on empirically derived velocity-depth relationships, meaning that the influence of local site conditions might not have been assessed correctly.

Overall, however, the ground-motion model of Boore et al. (2014) shows the lowest bias and seems to be the only model compatible with the observations for both PGA and longer period ground-motion. Its residual distribution is most likely to be Gaussian although showing larger variance. Therefore, we allow the equation of Boore et al. (2014) to serve as a first-order proxy for modelling ground-motion in the LRE. This method (named method 1 in the following) takes into account the effects of the sedimentary coverage using general empirical (i.e. non site-specific) amplification factors through parameters vS30 and z1. Note that the corresponding amplification factors of the ground-motion model of Boore et al. (2014) were calibrated using Californian data, meaning that any potential bias due to the differences between California basins and the upper Rhine graben is unknown. This obvious potential discrepancy has motivated the development of site-specific modelling based on the methodologies described below.

5 Site-specific ground-motion modelling (method 2)

Since a detailed subsurface model of the area of investigation is available, in a first step, we calculate ground-motions for soft rock conditions (taken as vS30 equal to 760 m/s and z1 = 0) using the ground-motion model of Boore et al. (2014). For the given values of vS30 and z1, the underlying site amplification for the given ground-motion model is unity (Boore et al. 2014). Herein, no regional correction has been applied since for the attenuation, as the results of data-driven regionalization schemes have corroborated the suggestion that the attenuation properties are similar to those of other active crustal regions, as discussed in Grünthal et al. (2018). Regional variations of ground-motion of active shallow earthquakes may further be significant only for distances larger than 50 to 60 km (e.g., Boore et al. 2014; Kotha et al. 2016) which are not considered here. For the linear component of the site amplification model in Boore et al. (2014), Seyhan and Stewart (2014) evaluated possible regional dependencies concluding that regional variations are insufficiently robust to justify the use of regional scaling.

Using relative 1D SH amplification functions with respect to a soft rock velocity of vS30 = 760 m/s (an example is shown in Fig. 4), we avoid any further host-to-target adjustments from soft to hard rock conditions, consistent with rock probabilistic seismic hazard analysis (PSHA) computations which are usually performed for vS30 = 800 m/s (e.g. Grünthal et al. 2018). Since site-specific amplification functions are available in the Fourier domain but GMPEs are displayed in the response spectrum domain, we follow the equivalent linear site response methodology proposed by Rathje et al. (2005) and Al Atik et al. (2014) based on the RVT and IRVT. This method allows for the calculation of Fourier amplitude spectra (FAS) compatible with given acceleration response spectra. A full seismological model (source, path and site) for the host region is not required. Although applying more advanced constitutive models with a larger number of inputs could potentially better capture the behaviour of the soil with respect to the equivalent linear approach, such procedure would result in increased parametric uncertainty. Moreover, equivalent linear site response analysis was considered to be sufficient due to the moderate to high soil stiffness with 96% of the sites having vS30 > 360 m/s. Weber (2007) has shown that the results of the equivalent linear approach are comparable to the predictions of the fully nonlinear site response analysis.

The following steps are applied:

  1. 1.

    For the considered scenario, the target response spectrum for standard rock conditions (vS30 = 760 m/s) is calculated.

  2. 2.

    For each site the IRVT is used to calculate the FAS that is compatible with the response spectrum defined in step 1 and implemented in the computer program Strata (Kottke and Rathje 2008). The problem of converting a response spectrum to a corresponding Fourier spectrum is addressed by using single-degree-of-freedom amplification functions which are narrowband for lightly damped systems approaching zero for frequencies larger than the site’s fundamental frequency. In this way, we limit the frequency range that contributes to the spectral acceleration for each single frequency. Wang and Rathje (2016) recently could show that the performance can be improved if the Vanmarcke (1975) peak factor model is used as an alternative to the Cartwright and Longuet-Higgins (1956) model as the Vanmarcke peak factor considers the statistical dependence between peaks which is important for narrow-band processes such as those associated with site response and oscillator frequency. A critical part of this approach is the computation of the root mean square (rms) of the oscillator frequency from the FAS through the duration of the oscillator frequency. While various models are available for defining rms duration models, we assess the duration based on the empirical ground-motion model of Kempton and Stewart (2006) which considers both the source duration as well as the increase in duration through vS30 (set to a soft rock reference velocity of 760 m/s) and z1.5 (i.e. the depth at which vS exceeds 1.5 km/s).

  3. 3.

    For each site, the FAS from step 2 is multiplied by the absolute value of the site-specific vS-Q-adjusted amplification function (an example can be found in Fig. 4) for taking into account site effects. Each site-specific amplification function is calculated with respect to a soft rock reference velocity of vS30 = 760 m/s. Since attenuation is stronger for the near-surface sediments than for the underlying solid rock, no additional κ adjustment is required (Al Atik et al. 2014).

  4. 4.

    The adjusted response spectrum (an example is shown in Fig. 6) for each site is obtained by applying the RVT to the amplification function obtained in step 3.

    Fig. 6
    figure 6

    Example for input response spectrum (solid line) and output site-specific response spectrum (dashed line) plus/minus one standard deviation for site S116 in Cologne-Deutz using the RVT approach (method 2)

    Full size image

6 Time-series approach based on broad-band ground-motion simulations (method 3)

In recent years, there is a growing trend towards the use of physics-based ground-motion models which can help to address the limits of empirical ground-motion modelling (Bradley 2019). Such approaches can be classified into three major categories: (1) physics-based approaches (Olsen et al. 2006, 2009) that incorporate the underlying seismological and geological information for specifying the complexity of the seismic source and the crustal structure, (2) simplified stochastic approaches (Boore 2003; Yamamoto and Baker 2013) based on semi-empirical models with few physical parameters and (3) so-called hybrid approaches (Graves and Pitarka 2010, 2015; Mai et al. 2010) which combine the first two approaches for covering both low and high frequencies.

We rely on the latter by applying the method proposed by Graves and Pitarka (2010, 2015) and implemented in the broad-band platform of the Southern California Earthquake Center (SCEC) for generating input acceleration waveforms for reference site conditions. The method has already been successfully validated against historical events in various tectonic environments (e.g., Graves and Pitarka 2015; Razafindrakoto et al. 2018; Lee et al. 2020) and it is also included as part of the SCEC broad-band platform validation exercise (Dreger et al. 2015; Goulet et al. 2015).

In broad-band ground-motion simulations, the most common way for including shallow site effects is via empirical amplifications factors based on ground-motion modelling results and site conditions defined according to geology (e.g. Hartzell et al. 2002) or vS30 (e.g. Graves and Pitarka 2010). More sophisticated approaches starting from vS30 before applying analytical site amplification models have recently been discussed (de la Torre 2020).

This empirical treatment is relatively simple with respect to the source and path modelling. For analytically assessing the influence of the local site response, for each studied site, the input acceleration time-series for reference site conditions are converted to a complex spectrum using a Fast Fourier Transform (FFT), bypassing the problems of the IRVT. The resulting complex Fourier spectrum is multiplied with the complex 1D SH amplification function for representing wave propagation to the ground surface. In this way, the phase modification from sedimentary layers is explicitly accounted for. Finally, the site-specific amplification function at each site is converted to an acceleration time-series and the corresponding response spectrum is calculated.

7 Definition of the scenario

In the LRE, seismicity is not evenly distributed, rather it shows concentrations on the western side and to the south-east of the LRE (so called Erft Block). Following Vanneste et al. (2013), the link between mapped faults and seismicity is clearest for the Erft fault. Located only 15 km west of the city of Cologne, the Erft fault system is the closest to the city and appears to be among the fastest slipping systems in the LRE (Vanneste et al. 2013, see Fig. 2). Following the definition of Schwartz and Coppersmith (1984), here we study a characteristic event on the Erft fault system with a given Mw 6.5 (Kübler 2013; Vanneste et al. 2013). Based on the regional magnitude-recurrence relationship (Grünthal et al. 2018), the average annual occurrence rate of such M ~ 6.5 event or greater would be in the order of one event every two thousand years.

Using typical values for building a set of scenarioruptures on a fault (i.e., aspect ratio 1.5, rupture spacing 2 km) for the underlying definition of the Erft fault in the German National PSHA (Grünthal et al. 2018), there are around 160 possible locations for such Mw 6.5 event. We decided for a relatively adverse case in which a multi-planar rupture starts in the middle of the fault (hypocentre location at 50.79° N, 6.74° E). Classically, for a Mw 6.5 event, the length of the fault is around 20 km and the down-dip width around 14 km (Wells and Coppersmith 1994). The top of the rupture plane is set to 4 km, consistent with typical hypocentres along the Erft fault at depths between 10 and 15 km (Hinzen 2003).

For the physics-based ground-motion modelling, the seismic source is prescribed in the form of a kinematic rupture description (i.e., each point of the fault is characterized by a source-time function describing the spatio-temporal evolution of the rupture) using a kinematic rupture taken from the stochastic slip generator (Graves and Pitarka 2015). Rupture parameterization is taken from the definition of the Erft fault (strike 147°, dip 57.5°, rake − 87°, Grünthal et al. 2018) using a generic 1D model of the Devonian bedrock since this type of rock was found to be representative for bedrock properties across the LRE (Weber 2007). The high-frequency source description utilized a stress parameter of 4 MPa. This value was set through calibration of the intensity-measure at short periods with the empirical ground-motion model of Boore et al. (2014), as we expect the contribution of the simulations mainly to occur at longer periods. Note, however, that this stress value is subject to uncertainties and it is slightly lower than the suggested average value for Europe of 5.65 MPa found by Bora et al. (2017). We use a suite of ten scenario input motions for accounting for the apparent aleatory variability in the occurrence of rupture scenarios and corresponding ground-motions.

8 Results

Site-specific spectral intensity values have been assessed from the simulated surface response spectra and from the simulated time series at each site at which a precise subsurface model is available. The spatial distributions for PGA and SA for T = 1 s are mapped in Fig. 7. For method 3, we show the corresponding mean values. A near-source and a distant site-specific example of the simulated time series as well as slip distributions and spectral intensity measures for all ten scenario realizations using method 3 are shown as supplementary material in the electronic version of this article.

Fig. 7
figure 7

Spatial distribution of spectral intensity using the ground-motion model of Boore et al. (2014) with vS30 and z1 (method 1, top), the RVT approach (method 2, middle) and physics-based modelling (mean of ten scenario input motions, method 3, bottom). The plots on the left represent PGA, the plots on the right show SA for a period T = 1 s. Please note the different amplitude scaling for PGA and SA. The yellow star represents the hypocentre location. The dashed rectangle shows the surface projection of the ruptured fault

Full size image

While close to the epicentre, method 1 provides smaller spectral acceleration values without any lateral variations, for methods 2 and 3, similar values of maximum spectral accelerations can be observed with a more heterogeneous spatial pattern. PGA further shows a rapid decrease over short distances mainly due to the strong attenuation in the sediments for the two latter methods for which the site-specific low values of QS are explicitly accounted for. This effect is less significant for the empirical ground-motion model used by method 1 since the properties of the strongly attenuating thick sediments are not fully considered. For the city centre of Cologne and the eastern city districts, PGA values from RVT modelling and from physics-based modelling agree well (PGA ≈ 0.1 g). Closer to the epicentre, the complexity of the multi-planar rupture associated with the source radiation pattern results in a lobular trend with largest spectral values of method 3 mapped for the eastern ends of the fault. Individual slip realizations (as shown in the supplementary material), however, can cause spectral intensity variations up to 40% at some sites due to the stochastic random-field. Since all events simulated by method 3 are based on bilateral rupture, the significance of the directivity is further controlled by the location of high slip patches and corresponding pulse-like features in the time series. For some rupture realizations, the radiation pattern of the shear dislocation on the fault can generate large forward-directivity velocity pulses at intermediate and longer periods (≥ 1 s) in the direction perpendicular to the fault plane, causing a larger motion in the strike-normal component of ground-motion (see the simulated velocity time series in the supplementary material in the electronic version of this article).

9 Discussion

Figure 8 illustrates the modelled ground-motion spectral amplitudes for six different periods as a function of the closest distance to the surface projection of the fault (Joyner–Boore distance Rjb). Site-specific analysis reveals a number of differences between the physics-based approach and the RVT approach. We further compare the results with the ground-motion model of Boore et al. (2014, method 1) in which the influence of site effects is empirically taken into account through a standard parameterization based on vS30 and z1.

Fig. 8
figure 8

Simulated and empirically predicted mean ground-motion spectral intensities for PGA (top left), SA (T = 0.3 s, top right), SA (T = 0.6 s, middle left), SA (T = 1.0 s, middle right), SA (T = 3.0 s, bottom left) and SA (T = 5.0 s, bottom right) as a function of the Joyner–Boore distance Rjb. Black dots represent the ground-motion model of Boore et al. (2014) with site-specific parameterization using vS30 and z1 from the velocity model of the LRE (method 1). Green crosses represent results of the RVT approach (method 2) and red symbols represent results of the physics-based modelling approach (mean of ten scenario input motions, method 3)

Full size image

As seen previously in Fig. 5, the chosen empirical ground-motion model generally underestimated predictions relative to ground motion observations for the validation suite of earthquakes used in Sect. 4. From Fig. 8, it is now visible that the empirical GMM produces lower predictions compared to the non-ergodic site response methods (methods 2 and 3), especially at intermediate periods (0.6 < T < 3.0 s). As shown in Fig. 2, since most of the sites in this study are located in the sedimentary basin whose thickness can reach up to several hundred meters, this supports the assumption that the influence of the soft soil layers on low-frequency ground-motion is adequately allowed for only when fully accounting for site effects caused by deep impedance contrasts. While for short spectral periods the differences between the empirical ground-motion model with the standard parameterization and the approaches based on methods 2 and 3 are less significant since the stress-drop has been chosen to be consistent with the Boore et al. (2014) predictions on rock and since vS30 can only account for site amplification at short periods. Both the RVT approach and the physics-based approach attenuate faster at larger distances. This is mainly due to the high attenuation of ground-motion (low values of QS) in the thick sedimentary cover.

In the considered period range, despite a large scatter, the RVT approach provides spectral intensities similar to the physics-based modelling approach. Figure 9 compares the site-specific response spectra with respect to the underlying rock reference conditions, i.e. Figure 9 displays how significant the influence of the local site conditions on the spectral intensity measures is considered by each method applied. While for very short periods the influence of site effects is similar for all three methods, larger spectral ratios can clearly be observed for the RVT and the modelling approaches for intermediate and longer spectral periods. This range of periods coincides with the fundamental resonance periods across the LRE with values around 5 to 6 s for its central part but decreasing to 1 to 2 s in its eastern part in the urban area of Cologne. The high values in the long-period range are most likely due to strong resonance effects caused by significant deep and internal impedance contrasts (taking values up to 6, Hinzen et al. 2004; Parolai et al. 2004) but they are also controlled by a rather wide amplification band of Fourier spectral ordinates (Bora et al. 2016). In turn, the impact of such strong impedance contrasts and corresponding site effects are not fully captured by the empirical modelling of ground-motion in the LRE (method 1) but can only be accounted for through site-specific modelling approaches given that measured values of sufficient accuracy are available.

Fig. 9
figure 9

Mean plus/minus one standard deviation of response spectral ratios of 670 sites across the LRE (black dots in Fig. 2) between site-specific vS30 and z1 (method 1, black line), site-specific RVT results (method 2, green line) and physics-based modelling results (method 3, red line) with respect to a ground-motion model with a reference velocity of vS30 = 760 m/s

Full size image

As one of the less constrained issues in rupture modelling is the treatment of aleatory variabilities of each source parameter, we try to quantify the effect of the variability of the random slip realizations generated by the slip generator (Graves and Pitarka 2015). As each of the ten underlying rupture realization varies in terms of the locations of high- and low-slip locations with differences up to a few kilometres along the fault plane (as described above, the length of the fault is around 20 km and the vertical extent is around 14 km), systematic discrepancies can be assessed. The different rupture realizations are mapped as supplementary material in the electronic version of this article. Based on the site-specific simulation observations of method 3, Fig. 10 shows the within-event residuals and the between-event residuals with respect to the RVT model using method 2. Thus, negative and positive between-event residuals correspond to underprediction and overprediction of method 3 with respect to method 2.

Fig. 10
figure 10

Distance dependence of the within-event residuals of method 3 for PGA (top left), SA (T = 0.6 s, top right) and SA (T = 3 s, bottom left). The red line represents the trend of the residual with Rjb. Bottom right: Between-event residuals trend of method 3 with period with respect to method 2

Full size image

The simulations reveal that the within-event component of ground-motion, i.e. azimuthal variations in source, path and site effects, displays a clear distance dependence although the residuals are rather stable across all periods. The slight bumps, which are obvious at Rjb ≈ 10 km for PGA and SA at a period of T = 0.6 s, might arise from the rupture process, which is simplified in the empirical ground-motion model, in turn leading to some systematic larger or lower amplitude values at distinct stations. At short and intermediate distances, the within-event variability, as expected, shows a systemic increase with period. Although in classical ground-motion models (methods 1 and 2), the within-event variability is not distance-dependent, Fig. 10 maps a maximum variability at short and intermediate distances for all periods due to the impact of the radiation pattern and directivity effects being strongest in the near-source region. On the contrary, for farther distances, fewer sites remain in the directivity direction due to the smaller dimension of the fault relative to the distance between the fault and the site. Hence, the variability decreases and it is mainly controlled by the radiation pattern shape and site complexities. Similar observations have been made by Imtiaz et al. (2015) and by Vyas et al. (2016) though for different magnitude and distance ranges.

The between-events residuals show a stable performance with values around zero, illustrating that, on average, the simulations are not biased in the period range across the simulated events and distance ranges considered. Since the between-event residuals display average source effects reflecting the influence of source factors such as variation of slip in space and time, the majority of this parameter uncertainty is mapped onto the between-event residual. At short periods (T < 1 s), the physics-based model is dominated by the portion of the simulation which relies on the simplified physics and corresponding stress parameter uncertainties. At longer periods (T ≥ 0.5 s), at which large amplifications are seen across the LRE (see Fig. 4), the slight increase of the between-event residuals and the increased variability might be attributed to the inclusion of amplification effects and due to the transition to simplified physics-based modelling (Razafindrakoto et al. 2018). The between-event standard deviation is smaller than the within-event variability which is consistent with the empirical results from GMPEs analyses. The between-event variability of method 3 reflects the variability resulting from various slip and hypocenter distributions. However, it does not include the potential variability due to further source parameters (e.g. stress drop). The calibration of the between-event variability, which is beyond the scope of the present study, implies the definition of the probability distributions of the source parameters of method 3 and an evaluation of the number of simulations needed to fully capture the impact of source variabilities.

When comparing the attributes outlined above with the results using empirically derived GMPEs, one can legitimately question whether an identified misfit indicates a problem with the simulations, a shortcoming in the GMPEs or maybe both. A critical consideration in such a comparison is the degree to which the effect under consideration (herein, a thick sedimentary cover in conjunction with a deep and intermediate strong impedance contrasts and the corresponding extension of duration of ground-motion) is well established in the empirical model given that the properties of the sedimentary cover are well constrained. This could be indicative of, for example, the amount of data which are available to constrain and calibrate those portions of the empirical models. Another consideration in comparisons of ground-motion models concerns conditions for which data are sparse or non-existent (here close distances to the fault), which is one of the principal situations under which physics-based simulations might be utilized. For such conditions, as can be seen above, both site-specific ground-motion modelling (method 2) as well as physics-based simulations (method 3) can reasonably explain differences to what is observed within the data space while only method 3 further allows quantifying seismic source uncertainties and the corresponding variability. The comparison between the results of method 1 (general empirical amplification based on vS30 and z1 empirically calibrated using Californian data) and methods 2 and 3 (using site-specific amplification functions) is also fully consistent with the GMPE testing performed in an independent way in Sect. 4. All results indicate that the latest generation of generic GMPEs developed to take into account thick sediment amplifications may underestimate the level of ground-motion in the LRE. Given the availability of a well-resolved subsurface model, the coupling between local 1D site response analysis and rock predictions (either empirical or physics based) are then more adapted to the challenging issue of broad-band ground-motion prediction in this area.

10 Conclusions

Taking advantage of a large amount of geophysical data collected in the area of the LRE, by combining digitized and revised soil profiles, a 3D velocity and attenuation model for the southern part of the LRE has been generated serving as a basis for calculating site-specific 1D SH amplification functions. The suitability of available ground-motion models for active shallow crustal earthquakes accounting for deep basin effects was assessed by comparing empirical ground-motion modelling results to seismic records of local events in the area. Thereon, a scenario-based deterministic framework was adopted for quantifying the impact of deep and spatially extended basins on ground-motion amplification. While empirical ground-motion models do not allow a full consideration of site-specific amplification phenomena in the area, we developed new methods coupling site-specific RVT site‐response analysis from the available 3D model with ground-motion predictions on rock (either empirical or physics-based). Resulting broad-band ground-motion modelling approaches provide similar spectral intensities over a broad spectral range. Although there is an absence of strong-motion recordings of damaging earthquakes in the region, results indicate that a site-specific approach across the sedimentary basin is essential for reliably assessing the level of ground-motion. Whilst rupture variability causes severe differences to empirical ground-motion models at short distances due to fault finiteness, for larger distances the significant attenuation of the thick sedimentary cover reduces the level of amplification, in particular in the high-frequency range, thus reducing the differences between the three methods applied. At intermediate and long periods, existing generic models with site effects taken into account empirically by vS30 and z1 provide significantly lower levels of ground-motion with respect to methods taking into account site-specific 1D amplification functions. Methods 2 and 3 should then be preferred to compute ground-shaking which might also include further work for obtaining better predictions accounting for the possibility of 2D/3D site effects. Though the empirical approach (method 1) can be faulted for being too simplistic, the reliability of such analytical approaches strongly depends on the availability of well-resolved site data. At short and intermediate distances (< 30 km), site-specific and hybrid physics-based ground-motions models (i.e. method 3) have the advantage to produce physics-based site-specific time-histories and to better capture the variability of ground-motions due to finite source effects.