Investigation of damage to the water network of Uki City from the 2016 Kumamoto earthquake: derivation of damage functions and construction of infrastructure loss scenarios

Abstract

The 2016 Kumamoto earthquake (main-shock: M_w 7.0, April 16th) has induced a widespread disruption of lifeline systems across the affected area. In Uki City (Kumamoto prefecture, Japan), water supply had been intermittently cut off for several days: as a result, around 50 repair operations on various locations of the underground pipeline system have been carried out by municipal services. In order to better constrain the vulnerability of such infrastructure with respect to future earthquakes, the collected empirical data is exploited to derive repair-rate functions for ductile pipelines (ductile iron and polyvinyl chloride) of small diameter (less than 100 mm). Due to the relatively low number of data points over a limited range of seismic intensity, the derivation of purely empirical damage function appears to be subject to significant statistical biases. Therefore, a Bayesian updating framework is adopted, where prior information on the parameters of the repair-rate function is estimated from existing damage functions from the literature. Moreover, the uncertainty related to the characterization of the Peak Ground Velocity at the location of the pipelines is taken into account by: (i) the generation of shake-maps with different assumptions on ground-motion prediction equations or fault models, and (ii) the inclusion of a spatially correlated field of the intra-event shake-map error term (i.e., modelling of the inherent variability of the seismic intensity). The results show that the derived repair-rate equation is consistent with some existing functions for ductile and earthquake-resistant pipeline segments. The effect of specific land conditions (e.g., topographic/geological factors) is also investigated, with the possibility to further parametrize the repair-rate function. Finally, the developed damage functions are applied to stochastic simulations of the seismic performance of the water network, while keeping track of various sources of uncertainties and quantifying their impact on the system’s loss distribution.

1 Introduction

Critical infrastructure systems such as utility networks have proven to be essential components of crisis management and recovery operations following an earthquake disaster. Due to the increasing interdependencies between systems, critical facilities such as hospitals or emergency centres may suffer from a prolonged loss of water or electrical power supply, even though the buildings’ structures are likely to withstand the seismic loading (in countries where strong seismic building codes are enforced). For instance, the M_w 7.0 main-shock of the 2016 Kumamoto earthquake that occurred in Kumamoto (Japan) on April 16th, led to the disruption of most utility services: electrical power and water supply were cut off for around half a million dwellings, and gas supply outage concerned around 100,000 dwellings, while most restoration operations lasted between several weeks and 2 months (source Asian Disaster Reduction Center).

Such events are far from exceptional in highly seismic areas such as Japan, and they raise the need for an accurate and precise assessment of the performance of critical utility systems like water supply networks. Seismic damage models for buried pipelines have been developed for a few decades, mostly under the form of repair-rate (RR) functions (i.e., expected number of leaks or breaks per km of pipeline), with empirical data collected from past earthquakes (e.g., Katayama et al. 1975; Isoyama and Katayama 1982; O’Rourke and Ayala 1993; Eidinger et al. 1995; ALA 2001; O’Rourke et al. 2012). These models have been the object of detailed reviews (Tromans 2004; Kakderi and Argyroudis 2014; Gehl et al. 2014), which contribute to raise several issues:

• (i) a significant variability is observed between the RR provided by different models (i.e., sources of epistemic uncertainty);

• (ii) most models rely on a limited number of data points, which are often extracted from a single earthquake event (e.g., Isoyama et al. 1998; O’Rourke and Jeon 1999; Pineda-Porras and Ordaz 2007);

• (iii) the dispersion associated with the regression from empirical data is most of the time not mentioned, leading to an underestimation of the uncertainty associated with the pipeline damage models.

The issue of epistemic uncertainties in the seismic loss assessment of infrastructure systems has recently been raised by Cavalieri and Franchin (2019), who have used a logic tree of various models (from seismic source parameters to fragility functions) and have applied Analysis of Variation to a virtual city comprising built areas and a water network. This procedure enables the identification of the most influential parameters on the outcomes of the risk analysis, and the authors have shown a significant impact of the variability between fragility models. In parallel, some studies have investigated the effect of uncertainties in the hazard estimation when deriving empirical fragility functions (i.e., estimation of the spatial distribution of the intensity measure (IM) of interest, following the earthquake event). This issue has first been tackled by Straub and Der Kiureghian (2008), who have proposed a statistical model that relies on statistical dependence between damage observations in order to derive fragility functions for electrical stations: to this end, an estimation error on the Peak Ground Acceleration (PGA) is introduced in order to account for the fact that the hazard estimates are obtained from ground-motion prediction equations (GMPEs) coupled with recorded observation at nearby sites (i.e., updated ground-motion field, or shake-map). When deriving fragility functions for buildings, explicit modelling of the uncertainty in the hazard estimation has also been proposed by Ioannou et al. (2015) and Yazgan (2015), who show that significantly flatter fragility functions are obtained as a result. More recently, Ioannou et al. (2020) have explored the building damage database for the 1980 Irpinia earthquake (Italy) in order to derive empirical fragility functions: they have tested statistical models of increasing complexity (e.g., uncertainty in the estimation of the IM, spatial correlation of the intra event residual, presence of recorded observations). To this end, a Bayesian updating framework, based on a Markov-chain Monte-Carlo (MCMC) sampling algorithm, has been developed in order to obtain posterior distributions of the fragility parameters.

Therefore, the main objective of this study is to apply a Bayesian updating method, based on developments similar to the approach by Ioannou et al. (2020), for the derivation of empirical RR functions for buried pipelines, using damage data from the Kumamoto earthquake main-shock. The Bayesian approach is well suited to the case where few data points are available, since the developed model can rely on the prior distribution that is estimated from the numerous RR functions available in the literature. Moreover, the uncertainty in the estimation of the IM is to be accounted for through ad-hoc shake-maps that are computed using records from KiK-net and K-NET stations (Aoi et al. 2004: NIED 2019) and various assumptions (i.e., fault geometry, GMPEs, soil amplification models). It is then expected that the posterior damage model, along with a proper uncertainty structure, may be applied to Japanese urban settlements with more confidence than currently available models. Moreover, thanks to the recorded and observed data from the earthquake, it is possible to replay the earthquake scenario with posterior hazard and damage models (i.e., shake-maps and updated RR functions) and to compare the projected losses with a priori scenarios that use generic models and parameters. A comparison between these two extreme configurations (i.e., no a priori knowledge vs. updated knowledge from observations) is expected to deliver valuable lessons on which components of the risk analysis chain have the most impact of the variability of the incurred losses to the water supply system.

Section 2 of the paper presents the water network of Uki City and the collected damage data, as well as the underlying assumptions and parameters that are considered for the computation of shake-maps. Then, Sect. 3 details the methodological developments carried out in order to apply a Bayesian updating approach to the damage data and to deliver updated RR functions for the buried pipelines. Finally, in Sect. 4, stochastic loss scenarios from the Mw 7.0 Kumamoto earthquake are generated, using two distinct sets of assumptions (i.e., a priori vs. a posteriori models and parameters): in both cases, Sobol’ indices (Sobol’ 1990) are computed in order to identify the contribution of each uncertain component to the total variability. To this end, two loss metrics are introduced for the water supply network, namely one based on aggregated physical damage (total number of repairs needed) and the other based on systemic behaviour (connectivity loss between sinks and sources).

2 Available data and modelling assumptions for the M_w 7.0 Kumamoto earthquake event

This section presents the characteristics of the water supply network of Uki City, in the Kumamoto Prefecture, where detailed damage data have been collected. It explains also the approach that has been chosen for the estimation of the hazard distribution (i.e., shake-maps derived from various assumptions).

2.1 Characteristics of the water network system of Uki City

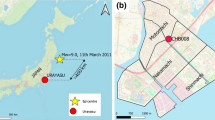
Uki City is a municipality of around 60,000 inhabitants located nearby Kumamoto City, for which the layout of the water supply network has kindly been made available for the purpose of this study (see Fig. 1). The network is roughly composed of two distinct parts, i.e. the Misumi area in the peninsula (Western part—around 130 km of pipelines) and the Matsubase area in the centre of the city (Eastern part—around 378 km).

Fig. 1

Situation of Uki City and of the water supply network with respect to the projected faulting of the M_w 7.0 Kumamoto earthquake main-shock (three different fault geometries considered)

Localized information (i.e., pipeline by pipeline) about the physical characteristics of the network, such as pipeline material, are not available. However, the post-earthquake account by Wham et al. (2017) delivers valuable information about the global characteristics of the network. The global distribution of pipeline materials is detailed in Table 1, where it can be noted that more that 90% of the pipelines in the main area (Matsubase) consist of ductile materials (ductile iron, polyvinyl chloride or steel). In terms of pipe diameter, also according to Wham et al. (2017), most pipelines are of small (73.5% between 30 and 100 mm) to moderate diameters (26% between 125 and 450 mm), with only a fraction of large diameter (over 500 mm) pipelines (0.5%): this distribution is corroborated by the information obtained from the municipality of Uki City, which has enabled the identification of the spatial localisation of the main categories of diameters (see Fig. 11).

Table 1 Distribution of material properties of the water pipelines in Uki City, from Wham et al. (2017)

2.2 Estimation of the ground-motion intensity around the water network

An estimation of the spatial distribution of ground-motion parameters is necessary in order to associate the location of the observed damage data with a range of IM. Since most RR functions available in the literature (Gehl et al. 2014) are expressed as a function of Peak Ground Velocity (PGV), it has been decided to select PGV as the IM of interest for the rest of the study.

After the earthquake occurrence, it is possible to make use of recorded ground motions at nearby stations in order to update the predicted ground-motion field and to better constrain the distribution of intensity measures (i.e., shake-maps). In the present case, available PGV shake-maps at a satisfying resolution may be retrieved from the U.S. Geological Survey ShakeMap^® service (Wald et al. 2006), or from the Japanese QuiQuake service (https://gbank.gsj.jp/QuiQuake). However, the USGS ShakeMap^® uses a site amplification model that evaluates V_S,30 from topographic slopes (Wald and Allen 2007): this approximation is efficient when no other soil data is available, but Japan benefits from a country-wide site amplification map at a resolution of 250 m (J-SHIS model, www.j-shis.bosai.go.jp/en/downloads). Moreover, the USGS ShakeMap^® only uses recorded data from the K-NET seismic network. The QuiQuake shake-map, on the other hand, exploits data from both K-NET and KiK-net networks and it relies on the J-SHIS site amplification model. However, the QuiQuake shake-map provides only median PGV values, with no indication of the standard-deviation values that are required in order to characterise the distribution of the IM.

Therefore, it is proposed to tailor specific shake-maps that fit exactly the needs of this study, with the site amplification model from J-SHIS, all recorded ground-motion parameters from K-NET and KiK-net, and a full probabilistic description of the distribution of PGV. To this end, the approach developed by Gehl et al. (2017) for the derivation of shake-maps using Bayesian networks is applied here: as demonstrated by the authors, this method generates an accurate probabilistic distribution of the updated ground-motion field, thanks to the Bayesian updating of the inter-event and intra-event error terms of the GMPE outcomes (i.e., a priori distribution of the ground-motion field). The ground-motion field is updated in the vicinity of the seismic stations thanks to the spatial correlation of the intra-event errors, and the global level of the ground-motion field is adjusted through the updating of the distribution of the inter-event error. This Bayesian approach uses very similar principles as the updating method proposed by Worden et al. (2018) for the version 4.0 of ShakeMap^®.

For the earthquake main-shock, PGV shake-maps are generated by considering a M_w 7.0 shallow strike-slip rupture. Recorded data from 83 K-NET and 22 KiK-net stations are exploited, by selecting the stations that are within 100 km of the epicentre. The exponential spatial correlation model by Jayaram and Baker (2009) is used, with a correlation distance d = 25 km for PGV. Two GMPEs are tested in the shake-map procedure, namely the global model by Chiou and Youngs (2008) and the specific PGV model that has been developed for Japan by Si and Midorikawa (2000). Source-to site distance metrics, such a distance to rupture R_rup and Joyner-Boore distance R_jb, are estimated from three different 3-D models of the fault geometry (see fault projection surfaces in Fig. 1), namely the source models proposed by USGS, by Kubo et al. (2016) and by Asano and Iwata (2016).

As a result, six different shake-maps are generated with different combinations of GMPEs and source models (see Table 2 and Fig. 2). Shake-maps generated with the Si and Midorikawa (2000) GMPE (S21 to S23) tend to predict PGV values and display stronger contrast between soil types: this difference may be due to the direct amplification factors that are used in Si and Midorikawa (2000), instead of V_S,30 values in Chiou and Youngs (2008). Also, the effect of the fault geometry on the shake-maps in near-field area is quite significant, with highest PGV values obtained when the Kubo et al. (2016) fault model is used. As a general comment, it is worth noting that large differences are observed between the six shake-maps, although the same processing method has been applied: this point reinforces the need to properly account for epistemic uncertainties, as well as aleatory (i.e. the standard deviation associated with the median PGV values), in the hazard assessment stage.

Table 2 Modelling assumptions for the six different shake-maps

Fig. 2

PGV shake-maps derived using the different assumptions on fault geometry and GMPEs

2.3 Reported damage to the water network system

The M_w 7.0 Kumamoto earthquake main-shock has led to water supply outage in thousands of dwellings, mostly in the central part of the city (Matsubase area). For several weeks and months following the event, municipal services have proceeded to the detection of leaks across the water network. As a result, dozens of repair operations have been carried out, mostly on the central part of the network, while the Western part (Misumi area) has been unaffected by the earthquake. Therefore, only the main network layout in the Matsubase area is considered in this study. The municipality of Uki City has provided an account of the repairs, which translate into 50 damage data points that are summarized in Fig. 3.

Fig. 3

Layout of the main part of the water supply network (solid black lines), with the observed damage locations (red diamonds). The underlying PGV distribution is based on shake-map S11

Additional data obtained from the municipality of Uki City have led to the identification of the characteristics (material type and diameter) of the pipelines where the repair operations have been performed. (see Table 7 in “Appendix”). It is observed that all damage points are related to small diameter pipelines (less than or equal to 100 mm). Moreover, almost all repairs concern PVC (polyvinyl chloride) and DI (ductile iron) pipelines, with the exception of a handful of pipelines for which the material is unknown. In addition, according to the collected data, larger pipelines appear to be made either of steel or other material, while the overwhelming majority (more than 90%) of small pipelines is made of either PVC or DI. Therefore, the collected damage data will be used to estimate RR functions for a limited type of pipeline, namely ductile pipes (PVC and DI) of small diameter (≤ 100 mm).

In Fig. 3, the damage locations are plotted with respect to the estimated PGV distribution from shake-map S11, as an example. Distinct pockets of damage may be seen across the network: two groups in the north, and one in the southeast. At first, there is no obvious trend between damage locations and PGV values, and some areas affected by the largest PGV (i.e., northeast of the network) have not sustained any damage. Other shake-maps, expressed in terms of PGA or Spectral Acceleration (SA) at various periods, have also been derived in order to check the correlation of other types of IM with the damage distribution; yet the results are not conclusive. It should be noted that no evidence of permanent ground deformation near the water network has been observed (source Disaster Information Laboratory—NIED), which is why the present study only concentrates on damage models due to wave propagation (commonly expressed as a function of PGV for buried pipelines).

3 Derivation of empirical damage functions for the water network

This section describes the method developed for the derivation of empirical damage functions, using the Uki City damage data. First, existing RR functions are used in order to build a prior distribution of the damage parameters. Then, a Bayesian updating approach is designed in order to develop posterior damage models under various assumptions.

3.1 Review of existing damage functions

Due to the characteristics of the water network (see Table 2) and the occurrence of the damage events, only RR functions for ductile pipelines with small-to-medium diameters are investigated. From the review of RR functions by Kakderi and Argyroudis (2014), the selected damage models are detailed in Table 3. Most of the equations take the form of RR = a.IM ^b, which is chosen as the underlying mathematical function to be characterized in the subsequent Bayesian framework. Most models provide a rough parametrization based on the type of material (or just brittle vs. ductile) and very few of them consider the pipeline diameter as a parameter. This level of detail is compatible with the level of knowledge that can be gained from the available characteristics of the network (see Sect. 2.1), and with the selected typology on which to estimate RR functions, i.e. ductile pipes (PVC and DI) of small diameter (≤ 100 mm).

Table 3 Summary of existing RR functions susceptible to be applied to the Uki City water supply network. CI, DI and PVC stand for cast iron, ductile iron, and polyvinyl chloride, respectively

Since the analysis is focusing on small diameter pipelines, all pipelines larger than 100 mm in diameter are not considered in the computation: as a result, the total exploitable length of the network is reduced to 276 km (as opposed to the total 378 km composing the main part of the network).

The above-detailed RR functions are empirically derived using data from past earthquakes. A common procedure consists in the approach proposed by O’Rourke et al. (1998), which follows these main steps:

• (i) identification of the locations of pipelines repairs and of the network layout;

• (ii) discretization of the area of interest into bins that are based on the level of the IM of interest;

• (iii) in each bin, associated with a discrete IM level, computation of the number of repairs and of the length of pipelines;

• (iv) in each bin, computation of the RR as the ratio of number of repairs over length of pipelines;

• (v) statistical regression over the RR data points in order to build the damage model.

Moreover, O’Rourke and Deyoe (2004) have introduced a criterion, based on the minimum length of pipelines that is required in order to derive statistically significant RR functions: (i.e., 95% confidence level that the RR is within ± 50% of the true value):

$$l \ge 15.36 \cdot \frac{1 - RR}{RR}$$

(1)

where l is the minimum number of kilometres of pipe in the bin, and RR is the repair-rate estimated within the bin.

The empirical approach based on discrete bins is tested on the Uki City damage data: the PGV range from shake-map S11 is divided into five discrete intervals, in which RRs are estimated (see Table 4). The first four bins show a regular progression of the damage rate, with RR values that are comparable with the ones from existing equations; however, the last bin implies a sharp decrease in the predicted RR, which is not physically meaningful. Also, the application of the criterion by O’Rourke and Deyoe (2004) reveals that only bin #4 contains enough data to be statistically reliable, and all other bins fail to meet the test. Therefore, this preliminary investigation shows that the damage data gathered from the M_w 7.0 Kumamoto earthquake main-shock is not sufficient to derive a fully empirical damage model.

Table 4 Discretised bins and associated damage data

3.2 Bayesian updating framework for the estimation of new parameters

As shown in the previous section, a higher-level statistical model is needed in order to cope with the limited amount of data. Therefore, a Bayesian updating framework is developed with the OpenBUGS software (Lunn et al. 2009). The global idea consists in generating a prior distribution of RR parameters from available equations in the literature, and in updating the distribution with the reported damage data and the corresponding ground-motion estimates. The Bayesian updating algorithm in based on the one initially developed by Ioannou et al. (2020) for the estimation of empirical fragility curves for buildings. The main differences reside in the use of an explicit spatial correlation model for the ground-motion field, and in the selection of a different probabilistic model for the sampling of damage states. In the case of linear components such as buried pipelines, it is commonly assumed to use a Poisson distribution in order to model the probability of component i to experience k damage events, given a mean rate λ_i (i = 1..N, with N the number of pipeline segments in the network):

$$P\left( {D_{i} = k |\lambda_{i} } \right) = \frac{{\lambda_{i}^{k} }}{k!}e^{{ - \lambda_{i} }}$$

(2)

The rate λ_i depends on the length L_i of the pipeline component and on the estimated repair rate RR_i:

$$\lambda_{i} = L_{i} \cdot RR_{i}$$

(3)

In the present application, the functional form RR = a.IM ^b is assumed, since it corresponds to a majority of the existing equations (see Table 3). The RR function is elevated to the logarithmic space, in order to improve the stability of the computation:

$$\ln RR_{i} = \ln a + { \exp }\left( {\ln b} \right) \cdot \ln PGV_{i}$$

(4)

Therefore, the variables θ = {ln a; ln b} constitute the parameters that need to be updated by the Bayesian algorithm.

The PGV field is provided by the shake-map estimates at the centroid of each pipeline segment i, with a median PGV value and an error rate ε_i:

$$\ln PGV_{i} = \ln \overline{{PGV_{i} }} + \varepsilon_{i}$$

(5)

At each site, the error term is decomposed into an inter-event term (η, common to all sites) and an intra-event term (ξ_i, specific to each site):

$$\varepsilon_{i} = \eta + \xi_{i}$$

(6)

The distribution of the terms η and ξ_i is directly provided by the shake-map outputs; while the spatial correlation between the ξ_i terms is approximated by a Dunnett–Sobel decomposition (Dunnett and Sobel 1955), as detailed by Bensi et al. (2011) and Gehl et al. (2018) in the case of spatially distributed systems. Given a spatial correlation matrix R between the N sites, and standard Gaussian variables w and v_i, the Dunnett–Sobel decomposition provides the following:

$$\xi_{i} = \sigma_{\xi } \cdot \left[ {\sqrt {1 - \mathop \sum \limits_{j = 1}^{m} t_{ij} } \cdot w + \mathop \sum \limits_{j = 1}^{m} t_{ij} \cdot v_{j} } \right]$$

(7)

where $\sigma_{\xi }$ is the standard-deviation of the intra-event error term (obtained from the GMPE) and the t_ij terms are the Dunnett–Sobel coefficients, which are estimated as follows:

$$r_{il} \approx \mathop \sum \limits_{j = 1}^{m} t_{ij} \cdot t_{lj}$$

(8)

where r_il is elements of the correlation matrix R, so that the t_ij coefficients may be approximated through an optimization routine. The number of common source random variables m constitutes a trade-off between the complexity o the model (i.e., computational cost) and the accuracy of the decomposition: for the present problem, m = 3 has been found to provide a satisfying approximation.

As a result, the statistical model that is built in OpenBUGS is represented in Fig. 4. It is a mix of deterministic variables (i.e., see Eqs. 3–7) and probabilistic variables, which are sampled through a MCMC scheme. The variables that model the uncertainty field in the shake-map, i.e. nodes u, v and w, are root nodes with a marginal distribution that corresponds to the standard normal distribution. Another root node, θ, has a marginal distribution that represents the prior distribution of the parameters ln a and ln b. This distribution is obtained by plotting all RR functions from Table 3 and by fitting parameters that correspond to the 16–84% confidence estimates of the plotted curves: as a result, a bi-variate normal distribution is adopted, with μ_lna = −8.09, σ_lna = 0.85, μ_lnb = 0.49, μ_lnb = 0.22 and ρ_{lna, lnb} = -0.74.

Fig. 4

Bayesian model implemented in OpenBUGS. Bold nodes represent stochastic variables, with their prior distributions. The blue node represents the damage variable evidenced from field observations

Evidence is inserted at the level of the D_i variable, where the number of reported repair operations for each pipeline segment is specified. Three MCMC chains are initiated, with different combinations of initial conditions (i.e., starting values of the probabilistic variables such as θ): each Markov chain is initiated with largely different values, in order to ensure that the three chains manage to converge to similar posterior distributions even though they originate from different regions of the space of variables. The Markov chain are built using the Gibbs sampling scheme in OpenBUGS, where variables are successively sampled from the posterior distribution of previous variables: the posterior distribution of a variable is obtained from the product of the prior distribution (e.g., initial estimate of θ) and the likelihood function (e.g., Eq. 2 for a given observation on a pipeline segment). Each chain generates 90,000 samples, from which the 30,000 first samples are removed (i.e., burn-in sequence of the chain). Out of the remaining 60,000 samples, only 1 out 500 samples is kept in order to reduce undesired auto-correlation effects. For both parameters ln a and ln b, the R_hat statistic is equal to one, indicating a satisfying convergence of the MCMC chains. As an example, generated samples from the three MCMC chains are represented in Fig. 5, along with the prior and posterior distributions of parameters ln a and ln b.

Fig. 5

Outcome of the MCMC sampling of RR parameters {ln a; ln b}, using shake-map S11

In Fig. 5, a slight shift of the mean of ln a and ln b is observed, while the generated samples show a smaller dispersion than in the initial distribution, thanks to the field observations. The Bayesian updating procedure is applied to each of the six shake-maps detailed in Sect. 2.2 (see Fig. 6). Some differences between the resulting RR functions are noticeable: in some cases, models show a significantly reduced dispersion (e.g., models on shake-maps S12, S21 and S22). Also, the model based on S11 predicts higher repair rates than others (e.g., S12 or S22). However, in general, all six models predict repair-rates that are below the median values of the equations from the literature, thus showing the relatively good performance of the pipelines during this specific earthquake event. Finally, the observed differences between the six models highlight the need to account for the uncertainties related with the ground-motion estimation, when exploiting empirical data.

Fig. 6

Median and 16–84th percentile RR functions obtained from the Bayesian model (solid and dashed blue lines), for each of the six shake-maps. The grey lines represent the prior distribution, obtained from the selection of existing RR functions

3.3 Bayesian updating framework accounting for different shake-map models

In order to account for the difference between the shake-maps, another statistical model is built with the addition of a variable S that represents the choice of the underlying shake-map (see Fig. 7). Therefore, S is a discrete variable with six possible states (i.e., from S11 to S23) with a uniform distribution, since there is no a priori knowledge of which shake-map version should be preferred.

Fig. 7

Bayesian model implemented in OpenBUGS, with an additional categorical variable S representing the underlying shake-map

This model is solved by using the same assumptions as the previous one, and the updated distributions are shown in Fig. 8. The integration of the variable S in the model leads to a single distribution of parameters ln a and ln b, which accounts for the contributions from the different shake-map versions. The samples generated by the MCMC chains are used to derive empirical distributions of RR, for each PGV value. Statistics are then extracted (e.g., 16th, 50th or 84th percentile) and the corresponding RR functions are plotted with respect to PGV. Finally, a least-square fitting of the curves is able to propose an analytical expression of RR = a.IM ^b, as detailed in Table 5. As observed in the previous section, the updated RR function tends to predict lower repair rates than most models retrieved from the literature. However, it is in good agreement with the damage models for ductile and earthquake-resistant pipelines, proposed by ALA (2001). In the right plot of Fig. 8, the updated distribution of variable S gives the posterior repartition of the six shake-maps, as a by-product of the Bayesian updating process. This result does not imply that some shake-maps are closer to the “truth” than others are, but it shows which shake-maps are more able to statistically explain the observed damage distribution across the water network. Shake-maps S21 and S22, based on the Si and Midorikawa (2000) GMPE that is derived from Japanese ground-motion records, have the largest weight after the Bayesian updating. They are followed by shake-map S11, which is based on the USGS fault geometry and on the Chiou and Youngs (2008) GMPE,

Fig. 8

Left: Updated RR function (solid and dashed blue lines) accounting for the different shake-maps, and prior existing RR functions (grey lines); Right: Posterior distribution of categorical variable S (i.e. weight of each shake-map in the sampling)

Table 5 Proposed RR functions for various percentiles, with PGV in cm/s

3.4 Bayesian updating framework accounting for specific soil conditions

Additional factors are investigated in order to better understand why specific clusters of damage location have been observed, especially in the North and Southeast part of the Matsubase network. To this end, a detailed map of the specific soil conditions around Uki City is superimposed on the observed damage locations (see Fig. 9). This soil condition map with the scale of 1:25,000 has been provided by Geospatial Information Authority of Japan (GSI) (2013). It is worth noting that most of damage has occurred on a handful of very specific soil types: 16 damages on Pleistocene low and medium terraces, 12 on reclaimed land, 8 on coastal plain and 7 on piled-up land.

Fig. 9

Detailed soil condition map for the central part of Uki City. The black dots represent the 50 damage locations that have been observed. Soil condition data by GSI (2013)

Therefore, another statistical model is built, by augmenting the Bayesian model of Fig. 7 with another variable representing the soil condition of each pipeline. An additional parameter K₁, representing the soil type, is then added to the functional form of the RR function:

$$RR = K_{1} \cdot a \cdot PGV^{b}$$

(9)

The parameter K₁ is only explicated for the soil types associated with the most damages (i.e., low and medium terrace, coastal plain, piled-up land, reclaimed land), while other soil conditions are aggregated into a common undefined category. This formulation is similar to the study, by Isoyama et al. (2000), who have introduced modification factors that account for the soil topography (e.g., terra, narrow valley, alluvial plain). The results of the Bayesian updating procedure accounting for the soil types are detailed in Fig. 10. A clear distinction between some soil types is observed, and the model predicts significantly higher repair-rates for reclaimed or piled-up land. However, the low amount of damage data for some soil types requires further investigation before consolidating this model. From Fig. 9, it can also be observed that most damage locations are close to the interface of contrasting soil types (e.g., between terrace and plain, or between natural levee and reclaimed land). Therefore, another statistical model using the interface between soil types as an additional modification factor would be useful, as it would be able to locate areas of larger damage likelihood with a higher accuracy. However, such a model would require a careful spatial study of the position of the damage locations with respect to soil type boundaries, while solving issues related to differences in spatial resolution.

Fig. 10

Median and 16–84th percentile RR functions obtained by discriminating different soil conditions

4 Main uncertainty sources in the generation of stochastic loss scenarios

This section recreates the Kumamoto earthquake scenario with the derived shake-maps and RR models, in order to compare the distribution of losses with the results that would be obtained when using a priori generic models. Various uncertainties sources at successive steps of the analysis are also investigated, so that their impact on the loss estimation may be quantified with respect to the level of knowledge that is available.

4.1 Summary of possible modelling options and uncertainty sources

In order to generate stochastic scenarios on the losses induced to the water network by the M_w 7.0 Kumamoto earthquake main-shock, six sources of uncertainty X_i are considered. These stochastic variables intend to cover aleatory and epistemic uncertainties, from the characterization of the earthquake event to the sampling of damages across the network:

• X₁ (epistemic, discrete): Fault geometry model to be used;

• X₂ (epistemic, discrete): GMPE model to be used;

• X₃ (aleatory, continuous): sampling of the inter-event error term in order to generate the ground-motion field;

• X₄ (aleatory, continuous): sampling of the intra-event error term in order to generate the ground-motion field;

• X₅ (epistemic, discrete): Damage model (i.e., RR function) to be used;

• X₆ (aleatory, continuous): sampling of the damage states of the pipelines from the RR function (i.e., application of the Poisson distribution).

In order to consider the impact of these variables on the loss assessment of the water network, two extreme cases representing various levels of knowledge are introduced:

• Case #1: No a posteriori knowledge of the event is available (e.g., no ground-motion records, no shake-map, no observed damage), which corresponds to an ex-ante risk assessment using only generic predictive models.

• Case #2: All a posteriori knowledge of the event may be used (e.g. shake-maps, updated RR function), which corresponds to an ex-post risk assessment that benefits from specific and updated models.

Depending on which case is considered, the stochastic variables X_i are sampled from various discrete or continuous distributions, as detailed in Table 6. It is worth noting that variables representing aleatory uncertainty (i.e., X₃, X₄ and X₆) are sampled in a similar way, whatever the case considered. However, regarding GMPE error terms (i.e., X₃ and X₄), uncertainties in Case #2 are slightly reduced thanks to the application of the shake-maps. Then, the intra-error term is sampled for each site i, while accounting for the spatial correlation between the sites. Finally, damage states (i.e., number of repairs following a Poisson distribution) are assumed to be sampled independently for each pipeline segment.

Table 6 Description of the variables to be sampled during the generation of the stochastic scenarios, for both Cases #1 and #2

4.2 Definition of system performance metrics

Two performance metrics are considered for the loss assessment of the water supply network, namely:

• M₁, the total number of repairs required along the network: it represents a global measure of the aggregated damage across the network. Such a metric is useful to estimate direct losses, which are related to the cost of physical repairs and to the amount of repair operations to be planned during the recovery phase.

• M₂, the number of water tanks (i.e., sources) disconnected from a given distribution node (i.e., sink): it represents a local measure, specific to each sink, which estimates the robustness of the network. This metric relies on a connectivity analysis between sources and sinks and it specifically accounts for the system’s topology and redundancy.

More elaborate system performance metrics for water supply networks are discussed in the review by Modaressi et al. (2014): measures based on flow analyses, such as the system serviceability index (Wang et al. 2010) which provides the proportion satisfied customer demands after an earthquake, are able to estimate accurately system-level losses. In the present case, however, only topological features of the network are exploitable (i.e., there is no information on the water demand from the various districts, or the direction of circulation of some of the pipelines), so that the connectivity analysis between sources and sinks can only provide a rough estimate of the performance of the system. For each pipeline segment, the occurrence of at least one damage point is sampled from the RR function, and it is assumed that a damaged pipeline is equivalent to a fully ruptured pipeline (i.e., no water flow between the edge’s extremities). Such an assumption is usually linked to the occurrence of actual breaks along the pipeline (as opposed to less severe leaks). Although the present study focuses on pipe leaks only (due to the absence of permanent ground deformation in the damaged areas), the assumption that pipe leaks are equivalent to flow interruption is supported by the fact that damaged sections of the network were quickly shut down in order to prevent water spillage and accelerate damage identification.

Since the estimated RR functions only pertain to small-diameter ductile pipelines, the computation of loss metrics M₁ and M₂ is only carried out on this pipeline typology, and pipelines of large diameter are considered as not vulnerable in the present example. Following the aforementioned assumptions, damaged pipelines are then removed from the adjacency matrix and the connectivity between various locations of the graph is computed, for each sampled damage scenario. This loss assessment procedure is based on the OOFIMS (Objet-Orient Framework for Infrastructure Modelling and Simulation) software, developed by Franchin and Cavalieri (n.d.) for the seismic risk analysis of spatially distributed systems. Using satellite imagery and indications on the network layout, 13 reservoir tanks are identified as the sources of the water supply system (see Fig. 9). In order to compute the performance metric M₂, four sinks (i.e., water distribution nodes) are then arbitrarily chosen, as detailed in Fig. 11: this selection leads to 13 × 4 couples of source-sink, for which connectivity analyses are carried out.

Fig. 11

Layout of the water supply network with the sources (reservoir tanks, green circles) and four sinks (distribution points, red stars)

4.3 Generation of loss scenarios

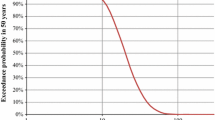
For each case detailed in Table 6, the stochastic variables are sampled from 50,000 Monte Carlo simulations, in order to get stable estimates of the two loss metric M₁ and M₂. The empirical cumulative distribution of metric M₁ is displayed in Fig. 12, for both cases. In Case #1, there is a large dispersion on the predicted number of repairs: possible values range from 22 (16th percentile) to 239 (84th percentile), with a median number of 78 repairs. For Case #2, the dispersion is strongly reduced (29 at 16th percentile and 79 at 84th percentile), while the median of 48 repairs is very similar to the 50 damage locations that have been actually observed. This finding is not surprising, since the collected damage evidence has been used to generate the same damage model that is injected in the forward analysis of Case #2. However, it provides a validation of the ability of the derived damage model and shake-maps to reproduce accurately the observed losses at a global level.

Fig. 12

Empirical CDF of loss metric M₁, for both cases #1 (in blue) and #2 (in red)

The same exercise is performed for loss metric M₂, with respect to the four selected sinks: the bar diagrams in Fig. 13 represent the proportion of damage scenarios that have led to a given number of disconnected sources from each sink, for both Cases #1 and #2. A qualitative analysis of the plots reveals that there are roughly two types of sink behaviours. Sinks #1 and #3 are located in secluded areas of the network, with often a single possible path from the sources to the sink: therefore, there is a tendency to disconnect all sources at once with only a few pipeline ruptures; while there is less chance that only a few sources are disconnected. On the other hand, sinks #2 and #4 are located in well-connected parts of the network, close to several reservoir tanks: it may happen that the connection to some of the sources is lost, however total disconnection from the network is much less frequent. When considering this loss metric, differences between Cases #1 and #2 are less obvious, although it is seen that fewer sources are disconnected in Case #2, which is in line with the lower damage distribution observed in Fig. 12.

Fig. 13

Distribution of loss metric M₂, for both cases #1 (in blue) and #2 (in red)

4.4 Computation of Sobol’ indices

In order to investigate the influence of each uncertainty source on the loss metrics in both cases, Sobol’ indices (1990) are estimated for the variables detailed in Table 6. Sobol’ indices provide a decomposition of the variance of a model output Y (e.g., M₁ or M₂) into fractions corresponding to uncertain inputs X_i:

$$Y = Y_{0} + \mathop \sum \limits_{i = 1}^{d} f_{i} \left( {X_{i} } \right) + \mathop \sum \limits_{j > 1}^{d} f_{ij} \left( {X_{i} ,X_{j} } \right) + \cdots$$

(10)

where d represents the dimension of the problem, i.e., the number of uncertain factors (here, d = 6).

The first-order term, represented by f_i(X_i) in Eq. 8, represents the main effect of factor X_i, while all subsequent interaction terms containing X_i represent the total effect of X_i. The Sobol’ indices are estimated thanks to Monte Carlo simulations with a design of experiment based on the d dimensions. In the case of spatially distributed and continuous variables X₄ (intra-event error at each site) and X₆ (damage sampling for each pipeline), the “categorical parameter” approach by Lilburne and Tarantola (2009) is applied: multiple possible maps of X₄ and X₆ are sampled, and each realization is associated with a categorical indicator that constitutes a pointer to the map in the design of experiments. The estimated Sobol’ indices, for both metrics and both cases, are detailed in Fig. 14.

Fig. 14

Sobol’ indices (main and total effects) computed for both cases and both loss metrics

For Case #1, the main contributors to the variability of loss metric M₁ are variables related to the hazard assessment part (X₁, X₂ and X₃), as well as the choice of the damage model (X₅): these variables influence the global level of hazard or damage rate, which is directly linked to M₁. On the other hand, the influence of variables X₄ and X₆ is negligible: it is because these variables are sampled across a spatialized field, so that there is an averaging effect that leads to very little impact on a global loss metric such as M₁. Loss metric M₂ presents a similar pattern, although variables X₄ and especially X₆ have more influence: due to the systemic nature of this loss measure, which is related to the topologic features of the network, the locations of the pipeline damages (i.e., represented by variable X₆) become important.

Regarding Case #2, only variables X₁ and X₅ have a significant influence loss metric M₁. From Fig. 2, it can be seen that the choice of the fault model (i.e., X₁) greatly influences the resulting shake-map, and in turn M₁. On the other hand, the influence of the choice of GMPE (i.e., X₂) is somewhat diminished by the ability of the shake-map to adjust the ground-motion fields from observations: as seen in Fig. 2, the shake-maps from the two different GMPEs predict similar ground-motion levels in the Uki City area. Similar comments can be made regarding the negligible influence of the GMPE error terms (i.e., X₃ and X₄), which are constrained by the shake-map algorithm. Variable X₅ has the largest relative weight, which means that further efforts should be made towards the reduction of uncertainties in the damage model, if the variability of M₁ needs to be reduced. When considering loss metric M₂ in Case #2, the largest relative weight represents the damage sampling (i.e., X₆): this aleatory uncertainty cannot be reduced and it directly governs the spatial distribution of damage across the network and the source-sink connectivity. All other variables have a reduced influence on the variability of M₂, which means that further reducing these uncertainties would not lead to a dramatic reduction in the dispersion of M₂, as long as damage is sampled for each pipeline. Therefore, there is a strong need to design more discriminating damage models, which use more factors than PGV or pipeline material and diameter: the investigation of the effect of specific soil conditions (i.e., Section 3.4) may provide some solutions, in order to refine the spatial distribution of damage.

5 Conclusions

Various types of data collected after the occurrence of the M_w 7.0 Kumamoto main-shock event (April 16th 2016) have led to the derivation of ad-hoc shake-maps, to the estimation of empirical RR functions and to the reconstruction of the earthquake loss scenario with various modelling assumptions. The application of a Bayesian updating framework to the derivation of empirical damage models is able to account for epistemic and aleatory uncertainties related to the ground-motion distribution (i.e., different choices of source geometry and GMPE, and distribution of inter- and intra-event error terms). Existing RR functions collected from the available literature constitute the prior distribution, which is used to build a robust posterior distribution of damage parameters from a reduced number of damage observations (i.e., only 50 damage locations over a 378 km pipeline network). In addition, the derivation of various shake-maps based on different modelling assumptions highlights the large variability in the ground-motion distribution, even when integrating post-earthquake information: this dispersion then induces a significant variability in the posterior distribution of the damage function. However, further refinement is possible by considering specific soil topography (i.e., additional modification factor based on soil type) or by investigating the effect of the transition areas between contrasting soil types. Globally, the derived damage models are comparable to existing RR functions, and they are in line with the models that are recommended for ductile and earthquake-resistant pipelines.

The second part of the study, devoted to the investigation of uncertainty sources when simulating loss scenario of the Kumamoto main-shock event with different levels of knowledge, has led to several noteworthy lessons:

• When considering a global loss measure that aggregates physical damage over the whole network (i.e., number of damages over all pipelines), the application of specific models that make use of all posterior observations provides accurate loss estimates with a reduced dispersion. The largest uncertainty sources remain the source geometry and the dispersion around the posterior RR function. The residual variability of the ground-motion field remains significant and it has a large influence on the loss distribution, even when accounting for dense ground-motion observations in seismically active areas like Japan.

• When considering local loss measures that are related to the system’s behaviour (i.e., connectivity analysis between a distribution node and water reservoirs), a reduction in the variability of predicted losses is also observed when post-event knowledge is available. However, this reduction is less obvious than in the case of a global loss measure. The sampling of spatialized variables, such as the intra-event error term or the damage state of each pipeline, generates disparate loss scenarios, which are difficult to constrain. As previously mentioned, a further parametrization of the RR function with the knowledge of specific soil conditions would be necessary in order to refine the location of most damage-prone areas. Indeed, the ultimate objective is to assess the network parts where damages are the most likely to occur, in order to take mitigation measures like renovating pipelines or increasing redundancy: however, as seen from the present results, current models are struggling to achieve this with enough accuracy, even when using all available post-earthquake information.

The present study has detailed a methodological framework for the Bayesian–based derivation of pipeline damage models: the RR function that has been built from the Uki City damage data might be applicable to other Japanese municipalities; however, one should be careful to apply the same range of ground motion level (i.e., PGV approximately around 25–75 cm/s) and to consider a similar distribution of pipeline material (i.e., mostly ductile iron and PVC). Another limitation lies in the use of damage data from a single earthquake, and the proposed damage model could be further refined by exploited data from other Japanese earthquake. Finally, the level of available data on the water supply system has prevented the application of flow-based loss measures such as the serviceability index: this measure is useful for managers of critical facilities like hospitals, in order for them to know the amount of water that is available and to plan ahead during the emergency phase. However, the simple connectivity analysis that has been carried out here is enough to highlight the challenges inherent to spatially distributed systems, from the point of view of uncertainty treatment and sampling of damage scenarios.

Appendix: Water network damage data

See Table 7.

Table 7 List of repair points on the water network, with material and diameter of corresponding pipelines