Dynamics of weak stability boundary transfer trajectories to Moon

Abstract

In order to design a WSB trajectory to Moon, highly elliptical geocentric orbit is propagated forward in time so that its perigee increases to Earth-Moon distance. Another highly elliptical selenocentric orbit is propagated backward in time till it starts moving towards Earth. The two trajectories are patched using Fixed Time of Arrival targeting method to obtain a WSB transfer trajectory. In this paper, various geocentric and selenocentric orbits are considered and eligible candidates for WSB transfer are represented on the phase space with color code on transfer time. Genetic Algorithm is used to find patching points to reduce the sum of $\Delta V$ required at the patching points. Lunar fly-by on the way to apogee is also studied.

Appendix:  Equations of motion

Restricted three-body problem (R3BP) and restricted four-body problem (R4BP) are the base models for construction of weak stability boundary transfer trajectories. In these models the orbits of Earth-Moon and Sun-Earth are considered to be circular and coplanar. But in actual solar system, Moon’s orbit eccentricity is 0.0055, Earth’s orbit eccentricity is 0.017 and the Moon’s orbit is inclined to Earth’s orbit by $5^{\circ}$. These values are low and so R3BP and R4BP can be considered as a good starting model. An orbit which becomes a real mission typically is obtained first in such an approximate system and then later refined through more precise models which include effects such as out-of-plane motion, eccentricity, other planet’s gravity, solar radiation pressure etc. However, tremendous insight is gained by considering a simpler model which reveals the essence of the transfer dynamics.

1.1 A.1 Circular restricted three-body problem (CR3BP) (Szebehely 1967)

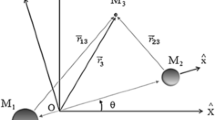
It is assumed that two massive bodies called primaries $m_{1}$ (more massive) and $m_{2}$ move in circular orbit about their center of mass (COM). The third body P is very small to affect the motion of other two bodies. Mass ratio of the system is given by

$$ \mu = \frac{m_{2}}{m_{1} + m_{2}}. $$

(14)

The masses of primaries $m_{1}$ and $m_{2}$ in this non-dimensionalized system of units are, respectively,

$$ \mu_{1} =1- \mu\quad \mbox{and}\quad \mu_{2} = \mu,\quad \mbox{where}\ \mu \in [0,1/2]. $$

(15)

1 unit distance = distance between $m_{1}$ and $m_{2}$.

Unit of time is such that the orbital period of $m_{1}$ and $m_{2}$ about their COM is $2\pi$.

Let $X$–$Y$–$Z$ be an inertial frame with origin at $m_{1}$–$m_{2}$ center of mass, where $X$–$Y$ plane is the orbital plane of the primaries. Consider the set of axes $x,y$ such that the $x$-axis lies along the line from $m_{1}$ to $m_{2}$ with $y$-axis perpendicular to it, completing a right-handed co-ordinate system. The $x$–$y$ frame rotates with respect to the $X$–$Y$ inertial frame with an angular velocity equal to the mean motion, $n$ of either mass. We refer to this co-ordinate frame as rotating frame.

Assume that the two frames coincide at $t=0$. Let ($X$, $Y$, $Z$) and ($x$, $y$, $z$) be the position of $P$ in the inertial and rotating frames, respectively. In normalized units, we have the following transformation of the particle’s position between two frames (Koon et al. 2006)

$$ \left ( \textstyle\begin{array}{c} X\\ Y\\ Z \end{array}\displaystyle \right ) = \left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c} \cos t & -\sin t & 0\\ \sin t & \cos t & 0\\ 0 & 0 & 1 \end{array}\displaystyle \right ) \left (\textstyle\begin{array}{c} x\\ y\\ z \end{array}\displaystyle \right ). $$

(16)

Differentiating gives the transformation of velocity components from the rotating to the inertial frame:

$$\left(\begin{array}{c}\stackrel{\mathbf{\cdot }}{X}\\ \stackrel{\mathbf{\cdot }}{Y}\\ \stackrel{\mathbf{\cdot }}{Z}\end{array}\right)=\left(\begin{array}{ccc}cost& -sint& 0\\ sint& cost& 0\\ 0& 0& 1\end{array}\right)\left(\begin{array}{c}\stackrel{\mathbf{\cdot }}{x}-y\\ \stackrel{\mathbf{\cdot }}{y}+x\\ \stackrel{\mathbf{\cdot }}{z}\end{array}\right).$$

(17)

The larger primary $m_{1}$, is located at ($- \mu_{2}, 0, 0$), and the smaller primary $m_{2}$, at ($\mu_{1}, 0, 0$). This is also true in the inertial frame when $t=0$. At general time $t$, the positions of $m_{1}$ and $m_{2}$ in inertial frame are respectively,

$$\begin{aligned} &(X_{1}, Y_{1}, Z_{1}) = (- \mu_{2} \cos t, -\mu_{2} \sin t, 0), \end{aligned}$$

(18)

$$\begin{aligned} &(X_{2}, Y_{2}, Z_{2}) = (\mu_{1} \cos t, \mu_{1} \sin t, 0). \end{aligned}$$

(19)

The gravitational potential which the particle $P$ experiences due to $m_{1}$ and $m_{2}$ (in normalized units) is

$$ U=- \frac{\mu_{1}}{r_{1}} - \frac{\mu_{2}}{r_{2}} - \frac{1}{2} \mu_{1} \mu_{2}. $$

(20)

where

$$ r_{1}^{2} = (x+ \mu_{2} )^{2} + y^{2} + z^{2}\quad \mbox{and}\quad r_{2}^{2} = (x- \mu_{1} )^{2} + y^{2} + z^{2}. $$

(21)

Consider Euler-Lagrange equations where the mechanical system is described by generalized co-ordinates ($q^{1},\dots,q^{n}$).

$$\frac{d}{dt}\frac{\partial L}{\partial {\stackrel{\mathbf{\cdot }}{q}}^i}-\frac{\partial L}{\partial q^i}=0.$$

(22)

Lagrangian $L = \mathit{KE} - \mathit{PE}$

Lagrangian in Inertial Frame:

$$\begin{array}{rl}\mathcal{L}(X,Y,Z,\stackrel{\mathbf{\cdot }}{X},\stackrel{\mathbf{\cdot }}{Y},\stackrel{\mathbf{\cdot }}{Z},t)& =\frac{1}{2}({\stackrel{\mathbf{\cdot }}{X}}^2+{\stackrel{\mathbf{\cdot }}{Y}}^2+{\stackrel{\mathbf{\cdot }}{Z}}^2)\\ & -\mathrm{\mho }(X,Y,Z,t).\end{array}$$

(23)

Lagrangian in Rotating Frame: (time independent)

$$\begin{array}{rl}L(x,y,z,\stackrel{\mathbf{\cdot }}{x},\stackrel{\mathbf{\cdot }}{y},\stackrel{\mathbf{\cdot }}{z})& =\frac{1}{2}({(\stackrel{\mathbf{\cdot }}{x}-y)}^2+{(\stackrel{\mathbf{\cdot }}{y}+x)}^2+{\stackrel{\mathbf{\cdot }}{z}}^2)\\ & -U(x,y,z)\end{array}$$

(24)

The Euler-Lagrange equations are given by

$$\frac{d}{dt}\frac{\partial L}{\partial {\stackrel{\mathbf{\cdot }}{q}}^i}-\frac{\partial L}{\partial q^i}=0,$$

(25)

$$\begin{array}{rl}L(x,y,z,\stackrel{\mathbf{\cdot }}{x},\stackrel{\mathbf{\cdot }}{y},\stackrel{\mathbf{\cdot }}{z})& =\frac{1}{2}({(\stackrel{\mathbf{\cdot }}{x}-y)}^2+{(\stackrel{\mathbf{\cdot }}{y}+x)}^2+{\stackrel{\mathbf{\cdot }}{z}}^2)\\ & -U(x,y,z),\end{array}$$

(26)

$$\frac{d}{dt}(\stackrel{\mathbf{\cdot }}{x}-y)-(\stackrel{\mathbf{\cdot }}{y}+x)+U_x=0,$$

(27)

$$\frac{d}{dt}(\stackrel{\mathbf{\cdot }}{y}+x)+(\stackrel{\mathbf{\cdot }}{x}-y)+U_y=0,$$

(28)

$$\frac{d}{dt}\stackrel{\mathbf{\cdot }}{z}+U_z=0.$$

(29)

On simplification, we have

$$\stackrel{\mathbf{\cdot }\mathbf{\cdot }}{x}-2\stackrel{\mathbf{\cdot }}{y}=-{\bar{U}}_x,$$

(30)

$$\stackrel{\mathbf{\cdot }\mathbf{\cdot }}{y}+2\stackrel{\mathbf{\cdot }}{x}=-{\bar{U}}_y,$$

(31)

$$\stackrel{\mathbf{\cdot }\mathbf{\cdot }}{z}=-{\bar{U}}_z,$$

(32)

$$\begin{aligned} &\overline{U} ( x,y,z ) =- \frac{1}{2} \bigl( x^{2} + y^{2} \bigr) +U ( x,y,z ), \end{aligned}$$

(33)

where $\overline{U}$ is the effective potential and the subscripts denote its partial derivatives. Since the equations of motion of CR3BP are Hamiltonian and independent of time, they have an energy integral of motion.

$$E(x,y,z,\stackrel{\mathbf{\cdot }}{x,}\stackrel{\mathbf{\cdot }}{y},\stackrel{\mathbf{\cdot }}{z})=\frac{1}{2}({\stackrel{\mathbf{\cdot }}{x}}^2+{\stackrel{\mathbf{\cdot }}{y}}^2+{\stackrel{\mathbf{\cdot }}{z}}^2)+\bar{U}(x,y,z).$$

(34)

Jacobi integral is given by

$$\begin{array}{rl}J(x,y,z,\stackrel{\mathbf{\cdot }}{x,}\stackrel{\mathbf{\cdot }}{y},\stackrel{\mathbf{\cdot }}{z})=-2E& =-({\stackrel{\mathbf{\cdot }}{x}}^2+{\stackrel{\mathbf{\cdot }}{y}}^2+{\stackrel{\mathbf{\cdot }}{z}}^2)\\ & -2\bar{U}(x,y,z),\end{array}$$

(35)

$$\frac{d}{dt}J=\frac{d}{dt}(-({\stackrel{\mathbf{\cdot }}{x}}^2+{\stackrel{\mathbf{\cdot }}{y}}^2+{\stackrel{\mathbf{\cdot }}{z}}^2)-2\bar{U}(x,y,z))=0.$$

(36)

This is the most important integral for determining the motion of the particle.

If $\phi (t)=(x(t),y(t),\stackrel{\mathbf{\cdot }}{x}(t),\stackrel{\mathbf{\cdot }}{y}(t))$, $t\in \mathbb{R}^{1}$, represent a general solution for (1), then $J ( \varphi ) =C$, where $C$ is a real constant. The set

$$\mathcal{J}(C)=\{(x,y,\stackrel{\mathbf{\cdot }}{x},\stackrel{\mathbf{\cdot }}{y})\in {\mathbb{R}}^4|J(x,y,\stackrel{\mathbf{\cdot }}{x},\stackrel{\mathbf{\cdot }}{y})=C\},$$

(37)

For a given value of $C$, represent a 3D energy surface in the 4D phase space.

There are no other integrals constraining the motion of the particle, making the CR3BP a non-integrable problem.

Lagrange points

There are five critical points of the effective potential—three points along the $x$-axis and two symmetric points off the $x$-axis. These points are the $x$–$y$ locations of the equilibrium points for a particle in the rotating frame, i.e., a particle placed here at rest with respect to $m_{1}$ and $m_{2}$ (zero initial velocity), will stay at rest for all time (zero acceleration). These points are labelled as $L_{i}$, $i = 1,\ldots, 5$. $L_{1}$, $L_{2}$ and $L_{3}$ lie on the line joining the two primaries while $L_{4}$ and $L_{5}$ form an equilateral triangle with the primaries. Let $E_{i}$ be the energy of a particle at rest at $L_{i}$, then $E_{5} = E_{4} > E_{3} > E_{2} > E_{1}$. Thus, $L_{1}$ is the location of the lowest energy equilibrium point and $L_{4}$ and $L_{5}$ are the highest energy equilibrium points.

1.2 A.2 Restricted four-body problem

1.2.1 A.2.1 Equations of motion in Sun-Earth rotating co-ordinate system (Koon et al. 2006)

In this model we suppose that the Sun and Earth are revolving in circular orbits around their barycentre and the Moon is moving in a circular orbit around the center of Earth. The orbits of all four bodies are in the same plane. Let $\mu$, $1- \mu$ and $m_{\mathrm{M}}$ be the masses of Earth, Sun and Moon, respectively. Let the distance between the Sun and Earth be unity. The distance from Earth to Moon is $a_{\mathrm{M}}$. In rotating co-ordinates wrt Sun-Earth system the positions of Sun and Earth are fixed at ($-\mu,0$) and ($1- \mu,0$), respectively. The angular velocity of the Moon in these synodic co-ordinates be $\omega_{\mathrm{M}}$ and the phase of the Moon at $t=0$ be $\theta_{\mathrm{M}0}$. In rotating frame defined above and using non-dimensional units the equations of motion are

$$\stackrel{\mathbf{\cdot }\mathbf{\cdot }}{x}=x+2\stackrel{\mathbf{\cdot }}{y}-c_{\mathrm{S}}(x+{\mu }_{\mathrm{E}})-c_{\mathrm{E}}(x-{\mu }_{\mathrm{S}})-c_{\mathrm{M}}(x-x_{\mathrm{M}}),$$

(38)

$$\stackrel{\mathbf{\cdot }\mathbf{\cdot }}{y}=y-2\stackrel{\mathbf{\cdot }}{x}-(c_{\mathrm{E}}+c_{\mathrm{M}}+c_{\mathrm{S}})y+c_{\mathrm{M}}{y}_{\mathrm{M}},$$

(39)

where $c_{i} = \frac{\mu_{i}}{r_{i}^{3}}$, for $i = \mathrm{E}, \mathrm{M}, \mathrm{S}$, and $\alpha_{\mathrm{S}} = \frac{m_{\mathrm{S}}}{a_{\mathrm{S}}^{3}}$, and

$$\begin{aligned} &r_{\mathrm{S}} = \sqrt{ ( x+ \mu_{\mathrm{E}} )^{2} + y^{2}}, \end{aligned}$$

(40)

$$\begin{aligned} &r_{\mathrm{E}} = \sqrt{ ( x- \mu_{\mathrm{S}} )^{2} + y^{2}}, \end{aligned}$$

(41)

$$\begin{aligned} &r_{\mathrm{M}} = \sqrt{ ( x- x_{\mathrm{M}} )^{2} + ( y- y_{\mathrm{M}} )^{2}}, \end{aligned}$$

(42)

with

$$\begin{aligned} &\mu_{\mathrm{S}} =1-\mu, \qquad \mu_{\mathrm{E}} =\mu,\qquad x_{\mathrm{M}} = a_{\mathrm{M}} \cos ( \theta_{\mathrm{M}} ), \\ & y_{\mathrm{M}} = a_{\mathrm{M}} \sin ( \theta_{\mathrm{M}} ), \qquad \theta_{\mathrm{M}} = \omega_{\mathrm{M}} t+ \theta_{\mathrm{M}0}. \end{aligned}$$

The values of the parameters are $\mu = 3.0359\times 10^{-6}$, $m_{\mathrm{M}} = 3.733998734625702\times 10^{-8}$, $a_{\mathrm{M}} = 2.573565073532068\times10^{-3}$ and $\omega_{\mathrm{M}} = 12.36886949284508$.

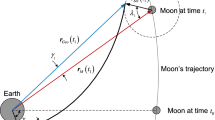
1.3 A.3 Fixed time of arrival targeting (Yamakawa 1992)

Suppose at initial epoch ($t_{0}$), position and velocity $(r(t_{0}), v(t_{0}))$ are given.

Transition matrix from $t_{0}$ to $t_{f}$ is

$$ \varPhi ( t_{f}, t_{0} ) = \left ( \textstyle\begin{array}{c@{\quad}c} \varPhi_{11} & \varPhi_{12}\\ \varPhi_{21} & \varPhi_{22} \end{array}\displaystyle \right ), $$

(43)

where $\varPhi_{i,j}$ are $3\times3$ partitioned transition matrix.

$$\begin{aligned} &\left ( \textstyle\begin{array}{c} dr ( t_{f} )^{-}\\ dv ( t_{f} )^{-} \end{array}\displaystyle \right ) = \varPhi ( t_{f}, t_{0} ) x (t_{0} )= \varPhi ( t_{f}, t_{0} ) \left ( \textstyle\begin{array}{c} dr ( t_{0} )\\ dv ( t_{0} ) \end{array}\displaystyle \right ), \end{aligned}$$

(44)

$$\begin{aligned} &\left ( \textstyle\begin{array}{c} dr ( t_{f} )^{+} \\ dv ( t_{f} )^{+} \end{array}\displaystyle \right ) = \varPhi ( t_{f}, t_{0} ) \left ( \textstyle\begin{array}{c} dr ( t_{0} )\\ dv ( t_{0} ) +d V_{0} \end{array}\displaystyle \right ), \end{aligned}$$

(45)

where $dV_{0}$ is velocity correction at $t_{0}$ and $dr$ and $dv$ are position and velocity deviations, respectively.

The objective is to cancel $dr(t_{f})^{+}$,

$$\varPhi_{11} ( t_{f}, t_{0} ) dr ( t_{0} ) + \varPhi_{12} ( t_{f}, t_{0} ) \bigl( dv ( t_{0} ) +d V_{0} \bigr) =0 $$

which yields

$$\begin{aligned} & \begin{aligned}[b] \varPhi_{12} ( t_{f}, t_{0} ) d V_{0} &=- \varPhi_{11} ( t_{f}, t_{0} ) dr ( t_{0} ) \\ &\quad {}- \varPhi_{12} ( t_{f}, t_{0} ) dv ( t_{0} ) ,\end{aligned} \\ &d V_{0} =- \varPhi_{12} ( t_{f}, t_{0} )^{-1} \bigl[ \varPhi_{11} ( t_{f}, t_{0} ) \varPhi_{12} ( t_{f}, t_{0} ) \bigr]x ( t_{0} ). \end{aligned}$$

When $dV_{0}$ is not performed at $t_{0}$, positional deviation at $t_{f}$ is

$$dr ( t_{f} )^{-} = \bigl[ \varPhi_{11} ( t_{f}, t_{0} ) \varPhi_{12} ( t_{f}, t_{0} ) \bigr]x ( t_{0} ). $$

Thus, velocity correction at $t_{0}$ is given as

$$ d V_{0} =- \varPhi_{12} ( t_{f}, t_{0} )^{-1} dr ( t_{f} )^{-}. $$

(46)

The time required to travel from starting point to end point is optimized using Nelder-Mead simplex method Lagarias et al. (1998) to minimize the total impulse required.