Ion acoustic kinetic Alfvén rogue waves in two temperature electrons superthermal plasmas

Abstract

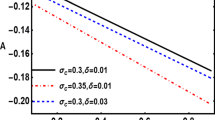
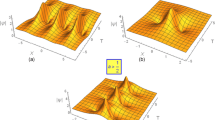
The propagation properties of ion acoustic kinetic Alfvén (IAKA) solitary and rogue waves have been investigated in two temperature electrons magnetized superthermal plasma in the presence of dust impurity. A nonlinear analysis is carried out to derive the Korteweg-de Vries (KdV) equation using the reductive perturbation method (RPM) describing the evolution of solitary waves. The effect of various plasma parameters on the characteristics of the IAKA solitary waves is studied. The dynamics of ion acoustic kinetic Alfvén rogue waves (IAKARWs) are also studied by transforming the KdV equation into nonlinear Schrödinger (NLS) equation. The characteristics of rogue wave profile under the influence of various plasma parameters ($\kappa_{c}$, $\mu_{c}$, $\sigma$, $\theta$) are examined numerically by using the data of Saturn’s magnetosphere (Schippers et al. 2008; Sakai et al. 2013).

Appendix

For the case of low beta plasma, the momentum equation is written as

$$ m_{i} \biggl( \frac{\partial \vec{v}_{i}}{\partial t}+(\vec{v}_{i} \cdot \vec{\triangledown})\vec{v}_{i} \biggr) =e(\vec{E}+ \vec{v}_{i}\times \vec{B}_{0}). $$

(50)

For motion perpendicular to the ambient magnetic field $B_{0}$, we can neglect the $(\vec{v}_{i}\cdot \vec{\triangledown}) \vec{v}_{i}$ term and Eq. (50) becomes

$$\begin{aligned} &m_{i}\frac{\partial \vec{v}_{i}}{\partial t}=e(\vec{E}+ \vec{v}_{i} \times \vec{B}_{0}), \end{aligned}$$

(51)

$$\begin{aligned} &m_{i}\frac{\partial }{\partial t}(\vec{v}_{i}\times \vec{B}_{0})=e\bigl[ \vec{E}\times \vec{B}_{0}+( \vec{v}_{i}\times \vec{B}_{0}) \times \vec{B}_{0} \bigr]. \end{aligned}$$

(52)

and the $x$-component of Eq. (52) is

$$ m_{i}\frac{\partial }{\partial t}(v_{iy}B_{0})=eE_{y}B_{0}-ev_{ix}B _{0}^{2}. $$

(53)

As we know that $E_{y}=0$, and we assume the infinite conductivity (Hasegawa and Uberoi 1982), therefore,

$$\begin{aligned} &\vec{E}+\vec{v}_{i}\times \vec{B}=0, \end{aligned}$$

(54)

$$\begin{aligned} &E_{x}+v_{iy}B_{0}=0, \end{aligned}$$

(55)

$$\begin{aligned} &v_{iy}B_{0}=\frac{\partial \phi }{\partial x}. \end{aligned}$$

(56)

Substituting Eq. (56) in Eq. (53), we get

$$\begin{aligned} &m_{i}\frac{\partial }{\partial t}\frac{\partial \phi }{\partial x}=-eB _{0}^{2}v_{ix}, \end{aligned}$$

(57)

$$\begin{aligned} &v_{ix}=-\frac{m_{i}}{eB_{0}^{2}}\frac{\partial^{2} \phi }{\partial x \partial t}. \end{aligned}$$

(58)

In normalized form, we obtain

$$ v_{ix}=-\beta \frac{\partial^{2} \phi }{\partial x \partial t} $$

(59)

which is Eq. (3) of Sect. 2