Sitnikov problem in the square configuration: elliptic case

Abstract

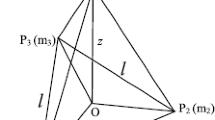
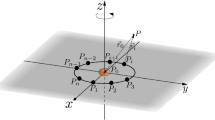
This paper is extension to the classical Sitnikov problem, when the four primaries of equal masses lie at the vertices of a square for all time and moving in elliptic orbits around their center of mass of the system, the distances between the primaries vary with time but always in such a way that their mutual distances remain in the same ratio. First we have established averaged equation of motion of the Sitnikov five-body problem in the light of Jalali and Pourtakdoust (Celest. Mech. Dyn. Astron. 68:151–162, 1997), by applying the Van der Pol transformation and averaging technique of Guckenheimer and Holmes (Nonlinear oscillations, dynamical system bifurcations of vector fields, Springer, Berlin, 1983). Next the Hamiltonian equation of motion has been solved with the help of action angle variables $I$ and $\phi$. Finally the periodicity and stability of the Sitnikov five-body problem have been examined with the help of Poincare surfaces of section (PSS). It is shown that chaotic region emerging from the destroyed islands, can easily be seen by increasing the eccentricity of the primaries to $e = 0.21$. It is valid for bounded small amplitude solutions $z_{\mathrm{max}} ( z_{\mathrm{max}} = 0.65 )$ and $0 \le e < 0.3$.

Appendix

First we expand the right hand side of Eq. (2) and then by putting the values of $r_{1} ( t ), r_{2} ( t ), r_{3} ( t ),\ldots$ . in the same equation, we get

$$\begin{aligned} r ( t )^{ - 3} =& a^{ - 3} \biggl[ 1 + \biggl\{ - e \cos t + \frac{e^{2}}{2} ( 1 - \cos2t ) \\ &{}+ \frac{3e^{3}}{8} ( \cos t - \cos3t )\\ &{} + \frac{e^{4}}{3} ( \cos2t - \cos4t ) +\cdots\biggr\} \biggr]^{ - 3}. \end{aligned}$$

Multiplying $z$ on both sides and applying the Binomial theorem, we get

$$\begin{aligned} r ( t )^{ - 3}z =& a^{ - 3} \biggl[ 1 + ( - 3 ) \biggl\{ - e \cos t + \frac{e^{2}}{2} ( 1 - \cos2t )\\ &{} + \frac{3e^{3}}{8} ( \cos t - \cos3t ) + \frac{e^{4}}{3} ( \cos2t - \cos4t ) \biggr\} \\ &{}+ 6 \biggl\{ - e \cos t + \frac{e^{2}}{2} ( 1 - \cos2t )\\ &{} + \frac{3e^{3}}{8} ( \cos t - \cos 3t ) + \frac{e^{4}}{3} ( \cos2t - \cos4t ) \biggr\} ^{2} \\ &{}- 10 \biggl\{ - e \cos t + \frac{e^{2}}{2} ( 1 - \cos2t )\\ &{} + \frac{3e^{3}}{8} ( \cos t - \cos3t ) + \frac{e^{4}}{3} ( \cos2t - \cos4t ) \biggr\} ^{3} \\ &{}+ 15 \biggl\{ - e \cos t + \frac{e^{2}}{2} ( 1 - \cos2t ) \\ &{}+ \frac{3e^{3}}{8} ( \cos t - \cos3t ) + \frac{e^{4}}{3} ( \cos2t - \cos4t ) \biggr\} ^{4}\\ &{} +\cdots \biggr]z. \end{aligned}$$

Solving the above equation and taking the terms proportional to $e^{\alpha'}z^{\alpha''} ( \alpha' + \alpha'' \le5 )$, we get

$$\begin{aligned} r ( t )^{ - 3}z =& a^{ - 3} \biggl[ 1 + 3e \cos t - \frac{3e^{2}}{2} ( 1 - \cos2t ) + 6e^{2}\cos^{2}t\\ &{} - \frac{9e^{3}}{8} ( \cos t - \cos3t ) - 6e^{3}\cos t ( 1 - \cos2t ) \\ &{}+ 10e^{3}\cos^{3}t - e^{4} ( \cos2t - \cos4t )\\ &{}+ \frac{3e^{4}}{2} ( 1 - \cos2t )^{2} - 15e^{4} \cos^{2}t ( 1 - \cos2t ) \\ &{}+ 15e^{4}\cos^{4}t - \frac{9e^{4}}{2}\cos t ( \cos t - \cos3t ) \biggr]z. \end{aligned}$$

Let us transform the higher power of the cosine function in linear form as

$$\begin{aligned} r ( t )^{ - 3}z =& a^{ - 3} \biggl[ 1 + \frac{3e^{2}}{2} + \frac{15e^{4}}{8} + 3e \cos t + \frac{9e^{2}}{2}\cos2t\\ &{} + \frac{27e^{3}}{8}\cos t + \frac{53e^{3}}{8}\cos3t \\ &{}+ \frac{7e^{4}}{2}\cos2t + \frac{77e^{4}}{8}\cos4t \biggr]z. \end{aligned}$$

Putting the semi major axis $a = 1/\sqrt{2}$ in the above equation one can find $\varpi^{2}$ and $f_{1} ( t )$.

$$\begin{aligned} r ( t )^{ - 3}z =& \biggl[ 2\sqrt{2} + 3\sqrt{2} e^{2} + \frac{15\sqrt{2} e^{4}}{4} + 6\sqrt{2} e \cos t\\ &{} + 9\sqrt{2} e^{2}\cos2t + \frac{27\sqrt{2} e^{3}}{4}\cos t\\ &{} + \frac{53\sqrt{2} e^{3}}{4}\cos3t + 7\sqrt{2} e^{4}\cos 2t \\ &{}+ \frac{77\sqrt{2} e^{4}}{4}\cos4t \biggr]z. \end{aligned}$$

Following the same procedure for the third term of Eq. (3), one can easily find $f_{2} ( t )$.