The effects of solar wind on galactic cosmic ray flux at Earth

Abstract

The amount of solar wind produced continuously by the sun is not constant due to changes in solar activity. This unsteady nature of the solar wind seems to be responsible for galactic cosmic ray flux modulation, hence the flux of incoming galactic cosmic rays observed at the top of the Earth’s atmosphere varies with the solar wind reflecting the solar activity. The aforementioned reasons have lead to attempts by several researchers to study correlations between galactic cosmic rays and the solar wind. However, most of the correlation studies carried out by authors earlier are based on the analyses of observational data from neutron monitors. In this context, we study the effects of solar wind on galactic cosmic ray flux observed at $r \approx 1~\mbox{AU}$, using a theoretical approach and found that the solar wind causes significant decreases in galactic cosmic ray flux at $r \approx1~\mbox{AU}$. A short time variation of the calculated flux is also checked and the result is reflected by exposing a negative correlation of the solar wind with the corresponding galactic cosmic ray flux. This means that the higher the solar wind the lower the galactic cosmic rays flux and vice-versa. To obtain a better understanding, the calculated flux and its short time variation at 1 AU are compared to data that shows a good fit to the model making it possible to establish a statistically significant negative correlation of $-0.988\pm0.001$ between solar wind variation and galactic cosmic rays flux variation theoretically.

1 Introduction

Modeling galactic cosmic rays is a highly non-trivial task which often requires a numerical simulation of the complex phenomena usually observed in the heliosphere. This can mainly be described in four processes namely (Parker 1965; Sabbah 2000; Bazilevskaya et al. 2013; Ihongo and Wang 2015; Aslam and Badruddin 2015) convection in the radial expanding solar wind, diffusion in the heliospheric magnetic field, particle drifts due to magnetic field irregularities and momentum change (or adiabatic cooling).

Nevertheless, if reasonable assumptions are implored, considering only the diffusion and convection processes, the complex phenomena can be reduced to a more simplified scenario which can then be modeled analytically as in the force field and convection-diffusion models (Caballero-Lopez and Moraal 2004; Bazilevskaya et al. 2013; Ihongo and Wang 2015).

Among these processes, the solar wind and magnetic field scattering are known to predominantly modulate the flux of galactic cosmic rays (Firoz et al. 2010; Alania et al. 2011; Modzelewska and Alania 2013). Cliver et al. (2013) also asserted that the solar wind is a solar driver of galactic cosmic ray modulation. In view of the above, this paper is mainly concerned with the effects of solar wind on galactic cosmic ray flux.

Here, we report on the flux of galactic cosmic ray protons calculated at $r \approx1~\mbox{AU}$ using the time-dependent force field model. The short time variation of the calculated flux at fixed energies is also studied together with the solar wind associated decreases observed on the flux while its relationship with the solar wind is also analyzed and the result is reflected by exposing a negative correlation of $-0.988 \pm0.001$ between the solar wind variation and the corresponding galactic cosmic ray flux variation at Earth. This relationship is finally used to predict galactic cosmic ray flux variation at Earth.

The flux is calculated for the energy range (0.5–100) GeV and the solar wind effect is predominantly visible at energies up to 20 GeV which may suggest that this analytical approximation appears to be suitable for this energy range.

2 Time dependent force field model

The time dependent force field model is an approximation to the Parker cosmic ray transport equation re-written below in its simplest form with no source term as (Parker 1965; Batalha 2012; Ihongo and Wang 2015)

$$ \frac{\partial f(\boldsymbol{r},P,t)}{\partial t} + \nabla\cdot \boldsymbol{S} - \underbrace{ \frac{1}{3} \nabla\cdot\boldsymbol{V} \frac{\partial f(\boldsymbol{r},P,t)}{\partial \ln P}}_{Q} = 0 $$

(1)

where (Caballero-Lopez and Moraal 2004; Ihongo and Wang 2015) $\boldsymbol{S} = 4 \pi P^{2} ( C \boldsymbol{V} f(\mathbf{r},P,t) -\boldsymbol {\kappa} \cdot\nabla f(\mathbf{r},P,t) )$ is the differential current density and $C = \frac{-1}{3} \frac{\partial \ln f}{\partial \ln P}$ is the Compton-Getting factor, $P$ is the rigidity and $Q$ is the term elucidating energy losses.

The time dependent force field model assumes the following to solve Eq. (1) after the current density $\boldsymbol{S}$ is inserted in to Eq. (1) (Ihongo and Wang 2015): There is a quasi-stationary state such that $\frac{\partial f}{\partial t} = 0$; There are no energy losses such that $\boldsymbol{\nabla} \cdot\boldsymbol{V} = 0$ for $r \geq1~\mbox{AU}$; Galactic cosmic rays are carried by the solar wind; The solar wind is radially dependent; No particle drifts; There may be a small anisotropy in the solar wind such that $V = V(r,\theta,\tau)$; The heliosphere is axially-symmetric in the heliocentric coordinate system where $\theta= \frac{\pi}{2}$; Isotropic and parallel diffusion coefficient; Perpendicular diffusion is negligible and Earth’s velocity influence is negligible compared to solar wind speed.

In order to solve Eq. (1), we apply the above assumptions after the differential current density is inserted and we perform a coordinate transformation to transform the time $t$ to a time $\tau$ in the solar wind frame.

The coordinate transformation is performed using the following transformation equations: $r \rightarrow r^{\prime}$, $t \rightarrow t^{\prime}$, $\theta\rightarrow\theta^{\prime}$, $\phi \rightarrow\phi^{\prime}$, $r^{\prime}= r$, $\theta^{\prime}= \theta$, $\phi ^{\prime}= \phi$ and $t^{\prime}= t - (\frac{r-r_{1}}{V_{1}(t)} )$ where $V_{1}(t) = V(r_{1},\theta_{1},\phi_{1}, t)$ and $r_{1}$, $\theta_{1}$ and $\phi_{1}$ are fixed.

This gives the following after the coordinate transformation and thorough simplification

$$ \frac{\partial f(r^{\prime},\theta^{\prime},P,t^{\prime})}{\partial r^{\prime}} + \frac{P V(r_{1}^{\prime},\theta_{1}^{\prime},t^{\prime})}{3 \kappa_{r^{\prime}r^{\prime}}}\frac{\partial f(r^{\prime},\theta^{\prime},P,t^{\prime})}{\partial P} = 0 $$

(2)

For brevity, we denote $t^{\prime}= \tau$, $r^{\prime}= r$, $\theta^{\prime}= \theta$, $\phi^{\prime}= \phi$ and $\kappa_{rr} = \kappa$ thus, Eq. (2) becomes

$$ \frac{\partial f(r,\theta,P,\tau)}{\partial r} + \frac{P V(r,\theta,\tau )}{3 \kappa}\frac{\partial f(r,\theta,P,\tau)}{\partial P} = 0 $$

(3)

where $V$ is the solar wind speed and $\kappa$ is the diffusion coefficient. Here, we adopt the form (Caballero-Lopez and Moraal 2004) $\kappa (r,P) = \kappa_{1}(r) \kappa_{2}(P)$, where $\kappa_{2} \approx P$, $P$ is the rigidity and $\tau$ is the solar wind time. It is transformed from the normal time $t$ to the solar wind frame.

The name force field originates from the fact that the coefficients of the second term in Eq. (3) has the dimensions of a force field (that is potential per unit length) while the time dependence emanates from the time dependent solar wind hence, the name “Time dependent Force Field Model”.

2.1 Time dependent force field solution

The general solution to Eq. (3) is

$$\begin{aligned} &{f(r,\theta,P,\tau)} \\ &{\quad{} = F \biggl( \theta,\underbrace{- \int\frac{V(r,\theta,\tau)}{\kappa_{1}(r)} \mathrm{d} r + 3 \int\frac {\beta\kappa_{2}(P)}{P} \mathrm{d} P }_{X} \biggr)} \end{aligned}$$

(4)

where $X$ is assumed to be a constant such that the general solution is

$$ f(r,P,\theta,\tau) = F(\theta,X) $$

(5)

Resulting in this specific solution

$$ \int_{P}^{P^{*}} \frac{\beta\kappa_{2}(P^{\prime})}{P^{\prime}} \mathrm{d} P^{\prime}= \int_{r}^{R} \frac{V(r,\theta,\tau)}{3 \kappa_{0}} \mathrm{d} r \equiv \phi(r,\theta,\tau) $$

(6)

where ∗ and $R$ are used in Eq. (6) to designate the values at the boundary of the heliosphere and outer heliospheric distance respectively and $r$ is the inner heliospheric distance fixed at 1 AU

From Eq. (6), let $\beta\approx1$, and $\kappa_{2}(P) \approx P$ (Caballero-Lopez and Moraal 2004) then we have

$$ \int_{P}^{P^{*}} \mathrm{d} P^{\prime}= \int_{r}^{R} \frac{V(r, \theta, \tau)}{3 \kappa} \mathrm{d} r^{\prime}$$

(7)

Now, from Eq. (7), let

$$ \int_{P}^{P^{*}} \mathrm{d} P^{\prime}= \int_{r}^{R} \frac {V(r,\theta, \tau)}{3 \kappa_{0}} \mathrm{d} r^{\prime}\equiv\phi(r, \theta,\tau) $$

(8)

This means that

$$ \phi(r, \theta,\tau) = \int_{r}^{R} \frac{V(r,\theta, \tau )}{3 \kappa_{0}} \mathrm{d} r^{\prime}$$

(9)

and

$$ \int_{P}^{P^{*}} \mathrm{d} P^{\prime}= \phi(r, \theta, \tau) $$

(10)

Substituting the limits of integration in to (9) and (10) yields

$$ P^{*} = P+ \phi(r,\theta, \tau) $$

(11)

and

$$ \phi(r,\theta, \tau) = \frac{V(r, \theta, \tau)}{3 \kappa}(R - r) $$

(12)

Note that $V$ is kept constant in the integration. Thus $\phi(r,\theta, \tau)$ in Eq. (12) is the main time dependent force field parameter.

The figure below explains the model’s general solution (Ihongo and Wang 2015).

The idea in Fig. 1 is that, a solution $f(R,\theta,\tau)$ is first obtained at the boundary and then used to obtain the solution $f(r,\theta,\tau)$ inside the heliosphere. We assume that particles travel only along the $z$-direction such that solar wind expansion is only radially dependent and both $\theta$ and $\phi$ are neglected.

Fig. 1

Illustration of the general analytical solution (Eq. (5)): The blue dashes is the inner heliosphere, the black is the outer heliosphere, $r,R,\tau$ are the inner heliospheric distance, outer heliospheric distance and the time transformed to the solar wind frame respectively. $X,Y,Z$ represent the heliocentric coordinate system where $\theta= \frac{\pi}{2}$

3 Results

The results presented here are based on two types of computations. These are: Computation based on the model and computation based on observational data.

3.1 Computation based on the model

The spectrum of galactic cosmic rays incident on the Earth’s upper atmosphere can best be studied as a function of its flux and the kinetic energy, this is to enable model results comparable to observational data. In this context, we present below, the model solution in terms of flux and kinetic energy of the particles with an aim to compare results based on our model with observational data.

The observed differential cosmic ray flux spectrum with respect to rigidity is defined as (Moraal 2013; Ihongo and Wang 2015):

$$ j(P)= P^{2} f $$

(13)

where $j(P)$ is the observed cosmic ray intensity spectrum with respect to rigidity, $P$ is the rigidity of cosmic ray particles and $f$ is the omnidirectional distribution function of cosmic rays.

Therefore, we can deduce the solution $f(r,\theta,P,\tau)$ from the aforementioned relation as

$$ f(r,\theta,P, \tau) = \frac{j(r,\theta,P, \tau)}{P^{2}} $$

(14)

Thus we write the solution $f(r,\theta, P, \tau) = f(R,P^{*})$ in terms of the particle rigidity as

$$ \frac{j(r,\theta,P, \tau)}{P^{2}} = \frac{j(R,P^{*})}{P^{*^{2}}} $$

(15)

where we designate the values at the boundary of the heliosphere using a “∗”.

Multiplying Eq. (15) by $P^{2}$, assuming that at the boundary of the heliosphere, the value of the radial distance becomes so large such that the boundary spectrum $j(R,T^{*})$ can be assumed to be independent of the radial distance yields

$$ j_{T}(r,\theta,P, \tau) = j\bigl(P^{*}\bigr) \biggl( \frac{P}{P^{*}} \biggr)^{2} $$

(16)

From Eq. (16), $j(P^{*})$ is the local interstellar spectrum of galactic cosmic rays and is also known as the value of the function at boundary of the heliosphere.

Now to obtain the spectrum inside the heliosphere at $\approx1~\mbox{AU}$, we define $P^{*}$ in Eq. (16) to take the form of (11) so that

$$ j (r, \theta, P, \tau) = j\bigl(P^{*}\bigr) \biggl( \frac{P}{P + \phi (r,\theta, \tau)} \biggr)^{2} $$

(17)

which is same as

$$ j (r,\theta,P, \tau) = j\bigl(P^{*}\bigr) \biggl(\frac{P^{2}}{P^{2} + 2 P\phi(r,\theta, \tau) + \phi^{2}(r,\theta, \tau) } \biggr) $$

(18)

Using the definition for $P$ in terms of kinetic energy $T$ as (Caballero-Lopez and Moraal 2004; Potgieter 2013; Moraal 2013; Aguilar et al. 2015) $P = \frac{A}{Ze} ( \sqrt{ T (T+2T_{0})} )$ where $A$, $Z$ are the mass and atomic numbers respectively of the protons to be considered and $T_{0}$ is the rest mass of a proton, we write the full solution in terms the particle kinetic energy as

$$ \begin{aligned}[b] &j (r,\theta,T,\tau)\\ &\quad = j\bigl(T^{*}\bigr) \biggl( \frac{T (T + 2T_{0})}{ T(T+2T_{0}) + 2 (\sqrt{T(T+ 2T_{0})})\varPhi+ \varPhi^{2}} \biggr) \end{aligned} $$

(19)

where $\varPhi(r, \theta, \tau) = \frac{Ze}{A} \phi(r, \theta, \tau)$, $Z$ and $A$ are the atomic and mass numbers respectively, $T$ is the kinetic energy and $j(T^{*})$ is the local interstellar spectrum. A local interstellar is an input spectrum at which an assumed modulation boundary is specified and then used to modulate the spectrum throughout the heliosphere (Potgieter 2013). This is usually computed using satellite or experimental data as it is yet to be measured directly although, one of the primary aims of the Voyagers is to measure the local interstellar spectra (Potgieter 2013). It has been parametrised by several researchers using observational data. Here, we have used the local interstellar formula for protons by Burger. This formula is written here in terms of rigidity $P$ as a function of Kinetic energy $T$ and units of Particles [$\mbox{m}^{-2}\,\mbox{s}^{-1}\,\mbox{sr}^{-1}\,(\mbox{GeV}/n)^{-1}$] as (Burger and Potgieter 2000; Usoskin et al. 2011; Maurina et al. 2014)

$$ j\bigl(T^{*}\bigr) = \frac{1.9 \times10^{4} \times P(T)^{-2.78}}{1 + 0.4866 P(T)^{-2.51}} $$

(20)

where $P(T) = \sqrt{T(T+2 T_{0})}$ and $T_{0}$ is the rest mass of a proton.

The result based on model computation is then computed using Eq. (19). Here, the solar wind $V(r, \theta, \tau)$ and $j(T^{*})$ are inputs. Solar wind data obtained from the ACE website: Srl.caltech.edu/ACE/ASC/rtsw.html for the month of May 2014 are used as input to the model, then the data from $\mathit{BESS}1998$ published in Sanuki et al. (2000) is used to compute the boundary spectrum $j(T^{*})$ for protons using Eq. (20). The kinetic energy $T$ used here are in the range (0.5–100) GeV and $\phi$ was computed using Eq. (12).

The fit to Eq. (19) is done using MATLAB 2014b and the following results are obtained (see Fig. 2).

3.2 Computation based on observational data

Here, the data values obtained from our model results using the fit from Eq. (19) are plotted alongside data points from AMS-01 (Alcaraz et al. 2000), BESS1993 (Anraku et al. 2002), BESS1998 (Sanuki et al. 2000), CAPRICE 1994 (Boezio et al. 1999), CAPRICE 1998 (Boezio et al. 2003) and IMAX1998 (Menn et al. 2000) using MATLAB 2014b for the galactic cosmic ray flux protons of $z=1$ in order to validate the model. The aforementioned data set can be found in the references provided.

For the flux variation, hourly values of cosmic ray intensity for the month of May 2014 obtained from Moscow neutron monitor (MNM); cro.izmiran.rssi.ru/mosc/main.htm and OULU neutron monitor (ONM); cosmicrays.oulu.fi are used.

Since neutron monitor counting rate are usually cosmic ray secondaries and because the model used primary inputs, the neutron monitor counting rates are recalculated to the heliosphere; that is to $\approx1$ AU. The process of recalculation is described below.

The magnitude of cosmic ray intensity measured by a neutron monitor is usually a function of the product of the differential intensity of cosmic ray at $r \approx1~\mbox{AU}$ and the specific coupling coefficient of the neutron monitor (Alania et al. 2008). This is written here as (Alania et al. 2008)

$$ j_{i}^{k} = A_{i}^{k} \int_{T_{\mathit{min}}}^{T_{\mathit{max}}} T^{-\gamma} W(T,h) \mathrm{d} T $$

(21)

where $j_{i}^{k}$ is the $k$ monthly or hourly values of intensity variation measured by $i$ neutron monitor, $T_{\mathit{max}}$ is the maximum kinetic energy or the upper limit of kinetic energy beyond which galactic cosmic ray intensity variation varnish. The maximum kinetic energy used in the context of Eq. (21) has been calculated using the definition for kinetic energy in terms of rigidity; (Aguilar et al. 2015) $T_{\mathit{max}} = \sqrt{P_{\mathit{max}}^{2} + T_{0}^{2}} - T_{0}$ for both Neutron monitors and $T_{\mathit{min}} = \sqrt{P_{\mathit{min}}^{2} +T_{0}^{2}} - T_{0}$ where $P_{\mathit{max}}$ is the maximum rigidity beyond which intensity variation varnish and this is usually assumed to be 100 GV (Alania et al. 2008), $P_{\mathit{min}}$ is the neutron monitor specific cut off rigidity, $T_{0}$ is the rest mass of a proton, $h$ is the atmospheric depth and $W(T,h)$ is the specific coupling coefficient of a neutron monitor. $A$ is the magnitude of galactic cosmic ray intensity recalculated to the heliosphere in other words, it is the primary cosmic ray intensity at $\approx1~\mbox{AU}$, $T^{-\gamma}$ is the primary power law kinetic energy spectrum at the boundary of the heliosphere and $\gamma$ is the spectra index of a neutron monitor.

The spectra index $\gamma$ of a typical neutron monitor is dependent on solar activity (Siluszyk et al. 2014). In this work we have used the value of $\gamma$ calculated for solar maximum for the year 2014 (Siluszyk et al. 2014). This gamma is $\gamma= -1.5$ thus;

$$ A_{i}^{k} = \frac{j_{i}^{k}}{\int_{T_{\mathit{min}}}^{T_{\mathit{max}}} T^{-\gamma } W(T,h) \mathrm{d} T} $$

(22)

But $W(T,h)$, the coupling coefficient of a neutron monitor has already been parameterized by various researchers . Here we have used the parameterisation by Maurina et al. (2014) obtained from the work done by Caballero-Lopez and Moraal (2012). This is written here as

$$ W(P,h)= 210^{-2} \bigl(2^{1.45} + P_{c} ^{1.45} \bigr)^{-4.696} P_{c}^{7.7} $$

(23)

where (Aguilar et al. 2015) $P_{c}(T) = \sqrt {T_{\mathit{min}}(T_{\mathit{min}}+2 T_{0})}$ is the specific neutron monitor cut off rigidity.

Using the parameterisation from Eq. (23) yields the coupling coefficients for Oulu neutron monitor at a cut off rigidity 0.8 GV and Moscow neutron monitor at a cut off rigidity of 2.43 GV as $1.20 \times10^{-8}~\mbox{m}^{2}\,\mbox{sr}$ and $3.57 \times10^{-6}~\mbox{m}^{2}\,\mbox{sr}$ respectively.

For convenience we drop $i$ and $k$ thus, evaluating the integral in Eq. (22), Eq. (22) becomes

$$ A = \frac{j}{W(T,h) [\frac{{T_{\mathit{max}}}^{-\gamma+ 1}}{-\gamma+1} - \frac{{T_{\mathit{min}}}^{-\gamma+ 1}}{-\gamma+1} ]} $$

(24)

where $A$ is the magnitude cosmic ray intensity recalculated to $\approx 1~\mbox{AU}$ that is; to primary cosmic ray intensity, $W(T,h)$ is the specific neutron monitor coupling function.

To test the accuracy of our calculation, it is affirmed that if $T_{\mathit{max}}$ and $\gamma$ are properly determined, the intensity of any neutron monitor recalculated to the heliosphere should be the same irrespective of their cut off rigidities (Alania et al. 2008). In this regard, Fig. 5 right panel shows that these intensities are the same which has proved the accuracy of the above calculations.

The cosmic ray intensities recalculated to primary intensities using Eq. (24) are then normalize with respect to minimum and maximum values in order to put to a standard scale of 0–1 using the following normalization relation (Moore 2006)

$$ \text{Normalized data} = \frac{j-j_{\mathit{min}}}{j_{\mathit{max}}-j_{\mathit{min}}} $$

(25)

where $j$ are the data values of cosmic ray intensity, $j_{\mathit{max}}$ is the maximum intensity in each data set and $j_{\mathit{min}}$ is the minimum intensity in each data set. These are presented in Fig. 3 top right panel while in Fig. 4, we have presented the actual intensities as percentages. The percentage intensities are calculated with respect to the hour of highest intensity using this relation (Alania et al. 2008), $j_{i} = \frac{j-j_{0}}{j_{0}}$ where $j_{i}$ is the percentage intensities, $j$ is the hourly average intensities and $j_{0}$ is the hour of highest intensity.

Figures 2, 3 and 5 presents both balloon borne experimental data and ground based neutron monitor count rates compared with the model results.

4 Discussion

Fig. 2

Time dependent force field Solution for galactic cosmic ray protons left panel, top right panel is the short time variation of flux calculated using the model and bottom right is the solar wind profile. The fit is done for: $T_{0} = 0.9384~\mbox{GeV}$, $R = 100~\mbox{AU}$, $r = 1~\mbox{AU}$, $\theta= \frac{\pi}{2}$, $\kappa= 8.4\times10^{21}\beta P~\mbox{cm}^{2}(\mbox{GV})/\mbox{s}$

Figure 2 left panel is a spectrum of galactic cosmic rays as a function of its flux and kinetic energy. This has been calculated as a function of flux and kinetic energy with an aim to compare results based on our model with observational data. As seen from the figure, the black curve is the local interstellar spectrum; This is an input spectrum at which an assumed modulation boundary is specified and then used to modulate the spectrum throughout the heliosphere (Potgieter 2013). This is usually computed using satellite or experimental data as it is yet to be measured directly, although one of the primary aims of the Voyagers is to measure the local interstellar spectra (Potgieter 2013). The colour code on the vertical axis are solar wind speeds corresponding to the coloured spectrum.

The solar wind is known to play a crucial role in controlling the mechanism of transport processes occurring continuously in the heliosphere (Mishra and Mishra 2006; Alania et al. 2011; Modzelewska and Alania 2013). These include convection in the solar wind, diffusion in the heliospheric magnetic field, drift motion due to magnetic field irregularities and adiabatic energy changes (Parker 1965; Sabbah 2000; Aslam and Badruddin 2015). However, among the aforementioned processes, the effect of solar wind remain the major process in cosmic ray intensity modulation (Sabbah 2000; Firoz et al. 2010). This effect is observed in Fig. 2 left panel where the flux is seen to bend over at low energies up to 20 GeV which may suggest galactic cosmic ray flux modulation by the solar wind at energies up to 20 GeV (Moraal 2013; Potgieter 2013). Due to the modulation effect, the coloured spectra are referred to as the modulated spectra while the black curve is usually referred to as the unmodulated spectrum (Caballero-Lopez and Moraal 2004; Moraal 2013). The spectrum is also observed to spread at the aforementioned energy range which may suggest that each solar wind speed produced a slightly different spectrum with the spectra decreasing with increasing solar wind speed. This may be due to the fact that the solar wind itself is not constant and this unsteady nature of the solar wind might be capable of producing variations on galactic cosmic ray flux (Firoz et al. 2010; Kojima et al. 2015). The coloured spectra is observed to harden above 20 GeV and the effect of modulation seems to vanish. This may be because the effect of solar modulation is expected to be very small and perhaps negligible above 20 GeV (Boezio et al. 2003; Aguilar et al. 2015).

For a better understanding, a short time variation of the calculated flux is presented in Fig. 2 right panel alongside the solar wind profile where a negative correlation between galactic cosmic ray flux variation and solar wind variation is observed. This is consistent with the negative correlation between solar wind variation and the corresponding galactic cosmic ray variation reported by other authors earlier (Sabbah 2000; Mishra and Mishra 2006; Firoz et al. 2010; Alania et al. 2011; Modzelewska and Alania 2013; Kojima et al. 2015). This means that the higher the solar wind the lower the galactic cosmic ray flux and vice-versa. This could be explained by the fact that low solar wind speed streams may be responsible for high cosmic ray intensities (HCRI) and high solar wind speed streams may be responsible for low cosmic ray intensities (LCRI) usually observed at Earth (Firoz et al. 2010; Kumar and Badruddin 2014). This also agrees with the report by (Mishra and Mishra 2006) that high speed solar wind streams might cause anisotropic variations in cosmic ray intensities. The abrupt decrease in flux observed at 250 hrs and 550 hrs may suggest the effects of high speed solar wind streams and perhaps due to enhancements in the solar wind speed (Mishra and Mishra 2006; Modzelewska and Alania 2013). High solar wind streams might have the effect of decelerating galactic cosmic ray flux (Firoz et al. 2010). The flux variation seems to be predominantly higher at low energies and lower at higher energies which may be due to variations in the solar wind speed as galactic cosmic ray flux is known to be strongly modulated by the solar wind at lower energies causing anisotropic variations in cosmic ray flux (Mishra and Mishra 2006; Firoz et al. 2010; Potgieter 2013).

In Fig. 3 left panel, the calculated flux is compared with observational data to validate the model. The model is seen to agree well with the IMAX 1992 data points up to 20 GeV and it is in good agreement with the rest of the data points up to 2 GeV. Between 2 GeV up 20 GeV, there are small discrepancies between the model, IMAX 1992 and the other data sets. This maybe because the inputs solar wind data used in the model were measurements during the period of solar maximum and the IMAX 1992 experiment was also during the period of solar maximum conditions while the other balloon flights were during the period of solar minimum (Boezio et al. 1999, 2003; Sanuki et al. 2000; Anraku et al. 2002). This may also be due to the fact that the period of solar maximum is known to be associated with high sunspot numbers and high solar radio flux (Tiwari et al. 2014) and since the above are inversely correlated with cosmic ray flux (Paouris et al. 2012; Tiwari et al. 2014), it might suggest that lower rate of cosmic ray flux are expected at solar maxima conditions and verse-versa. Also, weak detraction in cosmic ray flux may be responsible for rise in cosmic ray flux across solar activity minima and the strong detraction in cosmic ray flux maybe responsible for fall in cosmic ray flux across solar activity maxima (Sabbah 2000; Firoz et al. 2010). The high values of BEESS 1998 and AMS 1998 fluxes observed between 10–30 GeV maybe because these values were taken at the peak of solar minimum while all the coloured spectra becomes steeper above 30 GeV which might indicate the ascending phase of the solar cycle within which these measurement were taken (Tiwari et al. 2014).

Fig. 3

Left panel is the Calculated proton flux using the model red +, compared with data points from CAPRICE 1994 blue $x$, BESS 1993 green $o$, AMS 1998 red $o$, IMAX 1992 blue $o$, BESS 1998 cyan +, and CAPRICE 1998 magenta $x$. Top right panel are data points from OULU neutron monitor (ONM) and Moscow neutron monitor (MNM) compared with flux variation calculated from our model; these are normalized to standard scale of 0–1 and bottom right is the solar wind profile. The fit is done for; $T_{0} = 0.9384~\mbox{GeV}$, $R = 100~\mbox{AU}$, $r = 1~\mbox{AU}$, $\theta= \frac{\pi}{2}$, $\kappa= 8.4\times10^{21}~\mbox{cm}^{2}(\mbox{GV})/\mbox{s}$

In Fig. 3 top right panel, the short time flux variation calculated using the model (blue line) is compared with neutron monitor counting rates from Moscow and OULU neutron monitors. As seen from the figure, the model appears to be consistent with observational data except for the small discrepancies observed between 300–500 hours and between 650–720 hours. The possible interpretation for this is that low solar wind speed streams might cause high values of cosmic ray intensity while high solar wind speed streams might cause low values of cosmic ray intensity (Mishra and Mishra 2006; Firoz et al. 2010; Kumar and Badruddin 2014) as evident in the solar wind profile of Fig. 3 bottom right panel, the range where the discrepancies are observed corresponds to the period of low solar wind streams.

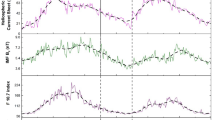
Figure 4 top left panel is the model’s actual hourly intensity variations without normalization, middle left and bottom left are the Moscow neutron monitor (MNM) and Oulu neutron monitor (ONM) counts respectively. The model flux is observed to vary faster with time at an average rate of 0.1 % hr⁻¹ while the NM counts are seen to be less varied with time at an average rate of 0.01 % hr⁻¹. This could be because solar wind speed variations maybe responsible for anisotropic variations on galactic cosmic ray intensity (Mishra and Mishra 2006; Firoz et al. 2010). This can be seen in Fig. 4 right panel where the solar wind speed variation is seen to be negatively correlated with galactic cosmic ray intensity variation.

Fig. 4

Hourly Intensity variations without normalization; top left panel is the model, middle left panel are data points from Moscow neutron monitor (MNM) and bottom left are data points from OULU neutron monitor (ONM) while the right panels are the aforementioned data points compared with the solar wind profile. The fit is done for; $T_{0} = 0.9384~\mbox{GeV}$, $R = 100~\mbox{AU}$, $r = 1~\mbox{AU}$, $\theta= \frac{\pi}{2}$, $\kappa= 8.4\times10^{21}~\mbox{cm}^{2}(\mbox{GV})/\mbox{s}$

Figure 5 left panel is the model’s main modulation parameter $\phi$ dependence on solar wind speed variation. This is observed to be linearly dependent on solar wind speed which means that the higher the solar wind speed the stronger the modulation parameter thus resulting in a stronger modulation of galactic cosmic ray flux by the solar wind. This thus, result in a negative correlation between galactic cosmic ray flux variation and solar wind speed variation which is in line with earlier report by Gupta et al. (2006), Firoz et al. (2010), Alania et al. (2011), Modzelewska and Alania (2013), Bazilevskaya et al. (2013), Tiwari et al. (2014), Kojima et al. (2015) that galactic cosmic ray intensity variation and solar wind variation are inversely correlated.

Fig. 5

Left panel is dependence of Model’s modulation parameter on solar wind speed, right panel is the recalculated Moscow neutron monitor (MNM) and Oulu neutron monitor (ONM) count rates

To calculate the exact correlation coefficient, the Pearson correlation method (Firoz et al. 2010) is used where a strong negative correlation coefficient of $r = -0.988 \pm0.001$ alongside its probable error was obtained. This is then tested for statistical significance also using the Pearson correlation method. Here, for the correlation coefficient of $r = -0.988$, the quantity $t = -172$ is calculated using (Moore 2006; Richard 2000–2012) $t = \frac{r}{\sqrt {\frac{(1-r^{2})}{N-2}}}$ where $N$ is size of the sample and $r$ is the correlation coefficient yielded a probability level of $p = 0.00000025$. This means that $p < 0.0001$ (Firoz et al. 2010). The possible statistical interpretation to the above is that the correlation between cosmic ray intensity variation and solar wind speed is statistically significant (Mishra and Mishra 2006). According to the Pearson correlation method, a correlation coefficient tends to be significant if the probability $p <0.05$ and if the probability is $p < 0.001$ then the correlation has a good statistical significance and even a better statistical significance for $p < 0.0001$ (Firoz et al. 2010). Our result of correlation is also in line with the earlier report by (Mishra and Mishra 2006) that the correlation between cosmic ray intensity and solar wind velocity is statistically significant.

The error of 0.001 obtained is computed using the probable error formula (Gupta et al. 2006) $P.E = \frac{0.6745(1-r^{2})}{\sqrt {N}}$ where $r$ is the correlation coefficient and $N$ is the size of the sample.

The over all result is that the model seems to be in good agreement with observational data which may suggest that the model provides a good approximation to the Parker transport equation (Eq. (1)) and may be suitable at short time scales and within the energy range used and in the model.

5 Summary

There have been several reports on cosmic rays and solar wind correlation from different researchers where negative correlations were found between cosmic rays and solar wind using observational data from ground based neutron monitors and experiments. In this context, applying a theoretical approach, we have studied the effects of solar wind on galactic cosmic ray flux at $\approx1~\mbox{AU}$ and found that the solar wind causes significant decreases on in galactic cosmic ray flux at $\approx1~\mbox{AU}$. A short time variation of the calculated flux is also checked at $\approx1~\mbox{AU}$ and the result is reflected by exposing a negative correlation of the solar wind variation with the corresponding galactic cosmic ray flux; This means that the higher the solar wind, the lower the galactic cosmic ray flux and vice-versa. For a better understanding, the model results are compared with observational data that shows a good fit to the model making it possible to predict that, galactic cosmic ray variation and solar wind variation at Earth are inversely-correlated and the correlation is found to be statistically significant with a correlation coefficient of $-0.988 \pm0.001$.