Modelling of Soot Aerosol Dynamics in Turbulent Flow

Abstract

Aerosol dynamics plays an important role in the modelling of soot formation in combustion processes, as it is responsible for predicting the distribution of size and shape of soot particles. The distribution is required for the correct prediction of the rates of surface processes, such as growth and oxidation, and furthermore it is important on its own because new regulations on particulate emissions require control of the number of smaller particles. Soot formation is strongly dependent on the local chemical composition and thermodynamic conditions and is therefore coupled with fluid dynamics, chemical kinetics and transport phenomena. Comprehensive modelling of soot formation in combustion processes requires coupling of the population balance equation, which is the fundamental equation governing aerosol dynamics, with the equations of fluid dynamics. The presence of turbulence poses an additional challenge, due to the non-linear interactions between fluctuating velocity, temperature, concentrations and soot properties. The purpose of this work is to review the progress made in aerosol dynamics models, their integration with fluid dynamics and the models for addressing the turbulence-soot interaction.

1 Introduction

Soot is particulate material formed during combustion processes. It consists mainly of carbon, a small amount of H and other compounds present in the fuel, and comprises primary particles, typically up to 50 nm, and aggregates ranging from several hundred nm up to a few μ m (Fig. 1). Its formation is strongly dependent on the local chemical composition and thermodynamic conditions, and is therefore intricately coupled with fluid dynamics and transport phenomena.

Fig. 1

TEM micrographs of soot particles (note that the big ‘holes’ are from the carbon film). Courtesy of Carlos E. Garcia Gonzalez [1]

Several reasons may be provided for the need to predict soot. First and foremost, soot emissions are harmful and must be minimised. While so far it was mainly the total soot mass that was being controlled, new regulations call for control of the number of particles, particularly the smaller ones, and therefore prediction of the soot particle size distribution is becoming increasingly important. On the other hand, soot can also be desirable: in furnace combustion it enhances heat transfer, while carbon black and other nanoparticles produced with similar processes are employed as advanced materials. It should also be mentioned that accounting for soot is necessary for the correct simulation of a sooting flame, as it affects the temperature field due to radiation.

In spite of controversy in the past, it is now generally accepted that soot is formed via poly-aromatic hydrocarbons (PAHs) and that C₂H₂ is instrumental in PAH and soot growth. Soot formation is kinetically controlled, and therefore cannot be predicted by equilibrium models. While chemical kinetics is clearly important, soot formation is also closely linked to the flow field. More specifically, the distribution and fluctuations of C₂H₂, PAHs and oxidisers in a turbulent flame are crucial for soot prediction. The effect of temperature on soot via kinetics and the reverse effect of soot on temperature via radiation also point towards soot being closely linked with flow and transport. The grave differences in the soot observed in different flow regimes and spatial locations in a flame indicate that soot prediction can only be accomplished in the context of detailed CFD models.

Soot particles are polydisperse, as can be clearly seen in Fig. 1. Accounting for the size and shape distribution of soot particles requires concepts from the subject of aerosol dynamics, which relate the evolution of the distribution to the physical and chemical processes that occur between aerosol particles, such as surface growth, coagulation and aggregation. The distribution is of fundamental importance for two reasons. Firstly, the rates of surface processes such as growth and oxidation depend on the surface area, while the coagulation and aggregation rates depend on particle volume, and therefore the distribution is an essential component of a detailed soot model. Secondly, prediction of the distribution is increasingly important on its own right, as new regulations are imposing limits on the concentrations of particles of different sizes, with increasing concern about the smaller particles; moreover, in the formation of nanoparticles for use as advanced materials, the distribution is a key property of the product and control over it allows tailoring the particles for specific applications.

A number of reviews on soot have appeared in the literature: [2, 3] are overall reviews of soot formation, [4,5,6,7,8,9,10] cover mainly soot chemistry and physics, while [11,12,13] focus on particular applications such as engines and coal combustion. Very few reviews have focussed on aerosol dynamics or on the coupling of soot models with fluid dynamics, the most relevant ones being [14], which reflects the state of the art in the late ‘90s when most models used in CFD did not incorporate detailed aerosol dynamics, and more recently [15] on fine particle formation (including both soot and metal oxides). The aim of the present review is to discuss the progress in the modelling of aerosol dynamics in the context of soot models and the coupling of aerosol and fluid dynamics, particularly for turbulent flows that present the most severe challenges. An overview of soot models will be presented first, followed by a brief summary of the essential chemical kinetics. Afterwards the main approaches for modelling aerosol dynamics will be discussed, with an emphasis on their application to soot. Subsequently the coupling of aerosol and fluid dynamics will be considered, with emphasis on turbulent flow, and the main challenges and unresolved issues will be identified.

2 Overview of Soot Models

2.1 Elements of soot models

The model of the fundamental physical and chemical kinetics of soot may be called the soot model and can be divided into two main parts: chemical kinetics and aerosol dynamics. The former can be further subdivided into kinetics of PAHs, nucleation and surface reactions including growth and oxidation. Not all models include detailed sub-models for all of these processes; PAH kinetics in particular are included in the more detailed models. A thorough discussion of soot kinetics is not the objective of this review, but a concise summary will be presented in Section 3 to provide the essential background for the material that follows. Aerosol dynamics studies how the soot particle population evolves as a result of the physical and chemical processes involved, which include, in addition to the processes mentioned above, coagulation and aggregation. The simplest models assume that soot is monodisperse, an assumption that can be used only in the context of empirical models. The prediction of the distribution requires solution of the population balance equation (PBE), a transport equation for the particle number density. Aerosol dynamics and the PBE are the main subjects in this review and will be discussed in Section 4.

Soot kinetics depend on the concentration of certain key species: nucleation and surface growth depend on precursors such as C₂H₂ and PAHs, while oxidation depends on oxidising agents such as O₂ and OH. The complexity of the gas-phase chemistry that is required in a simulation of a sooting process model depends on the soot model. The simplest models correlate soot with mixture fraction and require no more than a global mechanism, the precursor-based models require good predictions of C₂H₂ and therefore fairly detailed chemistry, while PAH-based soot kinetics need very detailed mechanisms.

When soot is formed and transported in a flow field, the kinetics and aerosol dynamics of the soot model must be combined with transport equations for soot and considered together with fluid dynamics, heat and mass transfer. A radiation model must be included to bring forth the two-way coupling of soot and temperature. Especially in laminar flows, accurate modelling of the transport processes is important. Differential diffusion between soot particles and gas-phase species must be considered, because the diffusivity of the former is much lower. Thermophoresis is also significant and contributes an extra flux term for the soot particles.

The presence of turbulence introduces a new level of complexity in soot modelling. In a turbulent flow, all quantities are subject to random fluctuations. Apart from the velocities, thermodynamic variables and concentrations, this includes the variables representing the soot (e.g. number density, volume fraction or particle size distribution). In Reynolds-Averaged Navier-Stokes (RANS) models, the effect of fluctuations at all scales is modelled, while in Large-Eddy Simulation (LES), the larger flow scales are simulated and the effect of fluctuations at the smaller scales is modelled. Turbulence models are now mature, while models for the turbulence-chemistry interaction have also undergone considerable development. By contrast, the interaction of turbulence and soot started to be investigated in detail relatively recently. This interaction manifests itself in the fluctuations of the soot variables, which result in several non-linear unclosed terms in the soot transport equations. One of the main objectives of this review is to outline pathways for modelling these terms.

2.2 Model taxonomy and historical overview

In a seminal review in 1997, Kennedy [14] classified soot models in three categories: empirical correlations, semi-empirical models and models with detailed chemistry. This classification reflected the state of the subject at that time, as empirical and semi-empirical models were dominant. Since then, significant progress has been made in detailed models; furthermore, empirical correlations relate soot to overall parameters (usually in engines) and are not suited for detailed coupling with fluid dynamics, so they will not be reviewed here. Therefore, for the purpose of this review, the models will be classified as follows:

• Semi-empirical non-precursor models. These models relate soot to temperature or mixture fraction.

• Semi-empirical precursor models. These models relate soot to precursors such as C₂H₂, albeit via empirical kinetics, and require coupling with relatively detailed chemistry.

• Detailed models. These are models that may include PAH chemistry, detailed soot kinetics and aerosol dynamics. They require coupling with detailed chemistry and therefore render the overall approach much more expensive. Many of the studies employing detailed models have been on 1-D laminar flows and ideal reactors, but there is also an increasing number of relatively recent works applying such models to turbulent flows.

The models now employed in research are mostly those belonging to the last two categories, while several models are hybrid, in the sense that they employ some but not all components of detailed models. This review will therefore focus on these two categories, although some of the models in the first category will be briefly discussed due to their historical importance.

3 Soot Chemical Kinetics

In this section, the elements of soot chemical kinetics will be summarised. As this is a vast subject and several reviews are available [4,5,6,7,8,9,10], no comprehensive review will be attempted here; only a summary of the main concepts essential for the understanding of the aerosol dynamics models will be presented. Each of the main chemical processes will be considered separately, except for the case of the semi-empirical non-precursor models, as those can only be described by overall equations.

3.1 Semi-empirical non-precursor models

Models in this category are largely outdated now for research purposes, although they are still implemented in general purpose CFD codes. Therefore only two of them will be considered here, due to their historical importance.

The model of Tesner et al. [16] postulates a chain reaction model for soot, adopting Semenov’s model for chain reactions. It links soot formation with temperature and proposes the following two-equation model for number density of ‘radical nuclei’ and soot particles. The model is empirical and does not reflect the true soot formation mechanisms. Nevertheless, it was used in the first studies of turbulent sooting flames [17, 18].

Proposed much later, the model of Moss et al. [19] is far more realistic, as it relates the rates of soot formation and growth to mixture fraction, and describes soot in terms of number density, n, and volume fraction, f_v. The equations are:

$$ \frac{d}{dt} \left( \frac{n}{N_{A}} \right) = \alpha - \beta \left( \frac{n}{N_{A}} \right)^{2} $$

(1)

$$ \rho_{s} \frac{d f_{v}}{dt} = \gamma n + \delta $$

(2)

where ρ_s is the soot density and N_A is Avogadro’s number. The mechanisms include nucleation (α, δ), surface growth (γn) and coagulation (β(n/N_A)²). The kinetic expressions for nucleation and growth relate the parameters α, γ and δ to temperature, density and fuel mole fraction, and these variables are in turn related to mixture fraction. The model makes an important step in modelling soot in terms of number density and mass fraction, a concept that was used in later models and can be related to the moment methods (Section 4.3.3). In addition, the link of soot to mixture fraction is a step towards linking soot with precursors, which are correlated to some extent with mixture fraction, although the concept of complete correlation between soot and mixture fraction is not realistic. Moss and co-workers later put forward more advanced semi-empirical precursor-based models (Section 3.4).

The model of Kennedy et al. [20] is a one-equation model that relates the soot volume fraction to mixture fraction. The lack of number density as a model variable makes it not very realistic, but the model is notable for leading to the first application of a transported probability density function (PDF) method to a sooting turbulent flame (Section 6.2). The use of one equation facilitated the application of the PDF method because, in early applications of PDF methods, the number of variables had to be kept to a minimum.

3.2 PAH formation

The subject of PAH kinetics is very large, and a detailed treatment is out of the scope of this review (see e.g. [21] or [8]). PAHs are hydrocarbons with two or more aromatic rings, and their role in soot formation is to bridge gas-phase chemistry and soot nucleation, as well as to contribute to soot growth via condensation. PAH kinetics is found only in detailed models. One major problem is posed by the large number of possible PAHs; furthermore, the transition from PAHs to soot is poorly understood, so a point of transition must be imposed.

Early detailed mechanisms of PAH formation were compiled by Harris et al. [22] and Frenklach and Warnatz [23]. The prototype detailed model for the growth of PAHs is the H-abstraction-C₂H₂-addition (HACA) mechanism [24,25,26]:

$$ \begin{array}{@{}rcl@{}} &&{\mathrm{A}_{i}} + \mathrm{H} \rightleftharpoons{~~~~} {\mathrm{A}_{i}\cdot} + \mathrm{H}_{2} \end{array} $$

(3)

$$ \begin{array}{@{}rcl@{}} &&{\mathrm{A}_{i}\cdot} + {\mathrm{C}_{2}\mathrm{H}_{2}} \rightleftharpoons{~~~~} {\mathrm{A}_{i}\mathrm{C}_{2}\mathrm{H}_{2}\cdot} \end{array} $$

(4)

$$ \begin{array}{@{}rcl@{}} &&{\mathrm{A}_{i}\mathrm{C}_{2}\mathrm{H}_{2}\cdot} + {\mathrm{C}_{2}\mathrm{H}_{2}} \longrightarrow {\mathrm{A}_{i+1}} + \mathrm{H} \end{array} $$

(5)

where A_i is a PAH with i aromatic rings. The HACA sequence can also include PAH oxidation. One implementation can be found in the ABF mechanism [27]. The growth of PAHs can be terminated at some point such as pyrene (four rings, C₁₆H₁₀), or further growth can be described as a polymerisation process via the method of moments [28, 29] (see Section 4 for further discussion). In one study [30], it was found that the difference of the two approaches in the soot production was up to a factor of two.

A simplified model due to Hall et al. [31], predicts two- and three-ringed PAHs ${\mathrm {C}_{10}^{~~~\bullet }\mathrm {H}_{7}}$ and C₁₄H₁₀, on which a nucleation model is then based. Steady-state assumptions for intermediates mean that only H₂, C₂H₂, ${\mathrm {C}_{6}^{~\bullet }\mathrm {H}_{5}}$ and C₆H₆ are needed. This model cannot be regarded as a detailed model in the sense of HACA, but it does represent a way of adding PAHs to precursors and was further developed by Smooke et al. [32].

Other detailed PAH mechanisms include those of Marinov et al. [33], D’Anna and Kent [34], Richter et al. [35], Slavinskaya and Frank [36] and Blanquart et al. [37]. A very detailed PAH mechanism can make the model very expensive, which is a concern for its coupling with CFD, especially in turbulent flows.

3.3 Nucleation

Nucleation, or inception, is possibly the most difficult step to model mechanistically, as there are many uncertainties such as the transition between PAHs and soot or the size of soot nuclei, while it is also very difficult to obtain experimental evidence. Furthermore, the nucleation mechanism depends on the fuel—in aliphatic fuels C₂H₂ appears to be the main species involved while in fuels containing aromatics, such as kerosene, the aromatic part of the fuel can be the dominant contribution [38].

In semi-empirical non-precursor models, nucleation is related to temperature or mixture fraction. In semi-empirical precursor models, nucleation is described via a global reaction involving C₂H₂ and sometimes also C₆H₆. The global reaction can be described as [39]:

$$ \mathrm{C}_{2}\mathrm{H}_{2} \longrightarrow 2\mathrm{C}(\mathrm{s}) + \mathrm{H}_{2} $$

(6)

$$ R_{n} = k_{n}(T) [\mathrm{C}_{2}\mathrm{H}_{2}] $$

(7)

where C(s) denotes the soot, k_n is given as a function of temperature, T, by an Arrhenius-type expression. In the model of Leung et al. [39], the size of nuclei was assumed to be 100 C, or 1.24 nm. The dependence of nucleation on C₂H₂ implies that this species must be accurately predicted, which is possible with modest-size reduced mechanisms, at least for simple fuels. An extension of this model, proposed by Lindstedt [40], includes also a benzene nucleation step. In the work of Hall et al. [31], the simplified PAH model described in Section 3.2 is combined with a nucleation model that relates nucleation to small PAHs. Nucleation rate is assumed to be eight times the formation rate of ${\mathrm {C}_{10}^{~~~\bullet }\mathrm {H}_{7}}$ and C₁₄H₁₀.

Mechanistic models consider nucleation as a series of PAH reactions, and are therefore closely related to PAH models. In the work of Frenklach and Wang [24], the soot nuclei are assumed to be formed by PAH dimerisation and the nucleation rates are calculated via aerosol dynamics equations (see Section 4). This concept is used in many subsequent works employing the method of moments. Another approach, found in the works of Richter et al. [35] and D’Anna and co-workers [41,42,43,44,45], is to integrate the nucleation steps with the kinetics of a detailed PAH mechanism.

3.4 Surface growth and oxidation

Early empirical models employed simplified expressions for surface growth that are now known to be unphysical. The Tesner et al. [16] model does not solve for volume fraction, hence has no notion of surface growth, while the Moss et al. [19] model considers growth as dependent on mixture fraction and temperature, but independent of surface area. The group of Moss, in the work of Syed et al. [46], employed a similar mixture fraction-based model, but with growth proportional to surface area.

A number of fundamental studies on soot surface growth have been carried out to investigate the identity of growth species, the dependence of soot on surface area, the reduction of soot reactivity with age, the difference of surface growth in premixed and non-premixed flames and the relative importance of nucleation and growth. A comprehensive study by Harris and Weiner [47, 48], based on laminar premixed flames, concluded that acetylene constitutes the primary growth species. An expression was postulated for surface growth that is linearly dependent on surface area, S, as well as on the concentration of acetylene, and has been the basis for many subsequent models:

$$ R_{g} = k_{g} S [{\mathrm{C}_{2}\mathrm{H}_{2}}] $$

(8)

In the Leung et al. [39] model, a square root dependence of growth on surface area was assumed, in order to limit growth. A subsequent study by Lindstedt [40], which considered acetylene and benzene nucleation steps, compared several growth expressions and found that a growth model independent of surface area yielded the best results in the context of that model. A later semi-empirical precursor-based model, due to Brookes and Moss [49], assumed growth to be proportional to Sⁿ and calibrated n from experiments yielding a value close to unity, i.e. growth proportional to surface area, as in the Harris-Weiner expression.

Most models for detailed surface growth kinetics are based on the HACA mechanism of Frenklach and Wang [24]. These models employ elementary reactions, based on an analogy with the HACA for PAH growth (Section 3.2). The HACA for soot can be summarised by the following steps:

$$ \begin{array}{@{}rcl@{}} {\mathrm{C}(\mathrm{s})-\mathrm{H}} + \mathrm{H} &\rightleftharpoons{~~~~}& {\mathrm{C}(\mathrm{s})\cdot} + \mathrm{H}_{2} \end{array} $$

(9)

$$ \begin{array}{@{}rcl@{}} {\mathrm{C}(\mathrm{s})\cdot} + \mathrm{H} &\longrightarrow& {\mathrm{C}(\mathrm{s})-\mathrm{H}} \end{array} $$

(10)

$$ \begin{array}{@{}rcl@{}} {\mathrm{C}(\mathrm{s})\cdot} + {\mathrm{C}_{2}\mathrm{H}_{2}} &\longrightarrow& {\mathrm{C}(\mathrm{s})-\mathrm{H}} + \mathrm{H} \end{array} $$

(11)

Further surface reaction steps are added to describe oxidation. The general form of rate equations for a soot particle of size class i is:

$$ R_{g,i} = k_{g,s} C_{g} \alpha \chi_{s} S_{i} N_{i} $$

(12)

where k_g,s is the per-site rate coefficient, C_g is the concentration of participating gas-phase species, χ_s is number density of surface sites obtained by a steady-state approximation, S_i is the surface area, N_i is the number density and α is a parameter interpreted to represent the effect of surface morphology. Initially α was a free parameter, and different values were used for different flames [24]; later it was assumed to depend on temperature and particle size [27].

Apart from the acetylene route, soot growth can also occur via condensation of PAHs on the surface of soot particles [24, 25]. Condensation can be modelled via aerosol dynamics (Section 4), where the participating particles are soot and PAHs.

In the mechanisms of Richter et al. [35] and D’Anna and co-workers [41,42,43,44,45], soot particles of different sizes are clustered into bins and included as species in the mechanism (see also Section 4.3.4), while growth occurs via reactions with C₂H₂ and PAHs. All of the processes in soot formation, from PAH kinetics to growth and even coagulation, are included in a single mechanism.

The main oxidising species of soot are considered to be O₂ and OH, while some models include also O. Two of the first models proposed for oxidation by O₂ were those of Nagle and Strickland-Constable [50] and of Lee et al. [51]. The model of Neoh et al. [52] is most commonly employed for oxidation by OH. These models form the basis for the oxidation part of most soot mechanisms, while several studies have proposed corrections to the rates in these models. For example, the Leung et al. [39] model included oxidation by O₂ only, according to the Lee et al. [51] model but with an adjusted constant, while the study of Liu et al. [53] considered oxidation by O₂ and OH and proposed further modifications, particularly for smoking flames. In detailed models, the oxidation steps are integrated in the surface chemistry via HACA.

4 Soot Aerosol Dynamics

In this section, the main approaches for introducing aerosol dynamics into soot models will be considered. The semi-empirical non-precursor and precursor models assume that soot is monodisperse. Proper account for aerosol dynamics requires solution of the Population Balance Equation (PBE) to account for the particle size distribution and, in more detailed descriptions, the morphology of aggregates.

4.1 Models assuming monodisperse soot

The Tesner et al. [16] model is formulated in terms of the empirical quantities of ‘radical nuclei’ and soot particles, so it cannot be discussed at all in terms of aerosol dynamics. For the other models that assume monodisperse particles, the coagulation rate has to be proportional to the square of the number of particles, as it is proportional to the number of collisions between particles. In the Moss et al. [19] model, for example, the coagulation rate is assumed to be temperature-dependent and is given by the following expression:

$$ R_{a} = C_{\beta}T^{\frac{1}{2}} \left( \frac{n}{N_{A}} \right)^{2} $$

(13)

where the coefficient C_β was determined from experiments with atmospheric ethylene flames.

4.2 The Population Balance Equation (PBE)

The Population Balance Equation (PBE), also called the General Dynamic Equation (GDE), describes the dynamics of a polydisperse particulate system. General reviews of the PBE can be found in [54,55,56,57], while [58] focusses on its coupling with reacting flows. The PBE is a general equation that has been applied to a wide range of particulate systems, often with a different terminology—for example, Williams’ spray equation [59] is a PBE for the droplet size and velocity distribution. The particles are described by one or more distributed properties, usually a measure of particle size (diameter, volume or mass). Other properties, such as the surface area and the number of primary particles per aggregate, can be used to include information about the particle morphology.

The physical and chemical processes described by the PBE can be classified in two groups. Processes in the first group result in transport in physical space and include convection, diffusion and thermophoresis. Processes in the second group are physical and chemical processes that result in changes in the distribution at each spatial point and include nucleation, continuous size change (surface growth and oxidation), particle combination (coagulation and aggregation) and possibly other processes such as breakage and sintering. The PBE will be considered first for a spatially homogeneous system such as a stirred reactor, where transport terms in physical space do not appear, and afterwards its coupling with flow will be addressed (Section 5).

4.2.1 Formulation of the PBE

The PBE can be formulated in a discrete or continuous form. The discrete form was developed first and is suitable for populations where polydispersity arises by successive additions of a certain unit. The particles can be described by a discrete distribution of the number of units they comprise. The discrete PBE first appeared in the work of Smoluchowski [60] on coagulation, and that form is often referred to as the Smoluchowski equation.

In the following we will consider particle volume, v, as the independent variable, taking discrete values v_i = iv₀ where v₀ is the volume of the unit. We define N_i as the concentration of particles of volume v_i (i.e. the number of particles per unit volume of physical space). The Smoluchowski equation is based on the physical argument that the rate of change of the number of particles v_i is determined by a source term due to coagulation of all pairs of smaller particles whose sum of volumes yields v_i and a sink term due to coagulation of particles v_i with any other particle:

$$ \frac{dN_{i}}{dt}= \frac{1}{2} \sum\limits_{j=1}^{i-1}\beta_{j,i-j}N_{j} N_{i-j} - \sum\limits_{j=1}^{\infty}\beta_{ij} N_{i} N_{j} $$

(14)

where the coagulation kernel, β_ij, is a function describing the probability of coagulation of a particle of volume v_i with one of volume v_j. While the original Smoluchowski equation considered coagulation only, it was extended by Friedlander [61] to include surface processes such as condensation and evaporation of aerosols, by assuming that these processes occur via addition or removal of a single unit. The discrete PBE is a system of ODEs that resemble chemical kinetics.

There are two main drawbacks in the discrete PBE formulation. The first one is the large number of variables and equations involved—for the coagulation of an aerosol ranging from 1 nm–1 μ m in diameter, 10⁹ discrete units must be accounted for. The second one is that, while a coagulation process results in a population comprising integer multiples of the volume of the nucleus, surface processes can involve the addition or subtraction of a much smaller unit—in the case of soot, that could be a C₂ unit or a C or even H atom, thus increasing the number of discrete units tremendously. The problem is aggravated in processes such as the evaporation of droplets, where a minimum discrete unit being removed cannot even be defined. The description of surface processes is therefore better accomplished by considering the particle volume as a continuous variable.

The continuous PBE is a partial integro-differential equation. We first define the number density, n(v,t), as a continuous function denoting the number of particles with volume in the interval between v and v + δv per unit of particle volume at time t, as shown in Fig. 2. Anticipating the coupling with fluid dynamics, it is advantageous to consider the number density as a concentration, i.e. as a quantity per unit volume of physical space. A correspondence between the particle concentration and the number density concentration is therefore established as:

$$ N_{i} = n(v_{i}) dv $$

(15)

Fig. 2

The continuous particle size distribution and its time evolution

A concise derivation of the continuous PBE is given in the Appendix. The final equation including surface processes, nucleation and coagulation is:

$$ \begin{array}{@{}rcl@{}} \frac{\partial n}{\partial t} + \frac{\partial (Gn)}{\partial v } &=& B \delta(v-v_{0})\\ &&+ \frac{1}{2} {{\int}_{0}^{v}} \beta (w,v-w) n(w) n(v-w) dw - {\int}_{0}^{\infty} \beta (v,w) n(v) n(w) dw\\ \end{array} $$

(16)

where the function G is the net rate of change of particle volume due to a continuous process, such as growth and oxidation, and has the role of a convective velocity in the particle volume coordinate. Nucleation is assumed to produce particles of volume v₀ with rate B. The integral terms on the right-hand side correspond to the sums in Eq. 14, and the possible forms of the kernel β(v,w) will be considered in Section 4.2.2. In the remaining of this review we will refer almost exclusively to the continuous PBE, and therefore the distinction between the two forms will not be mentioned explicitly except where it needs to be emphasised. In the case of soot, the PBE must be coupled with the species mass balance equations and the chemical kinetics of the gas phase. The nucleation, growth the oxidation rates will thus be functions of the species mass fractions, furnished by the kinetic models described in Sections 3.3 and 3.4.

Several extensions to the form of the PBE shown in Eq. 16 are possible. Further integral terms can be introduced to describe breakage processes, but have not been used in soot modelling. The PBE can also be extended to several dimensions if a joint distribution in terms of additional variables—e.g. volume, surface area or chemical composition—is considered. While the formulation of the multidimensional PBE is straightforward, such a model requires sufficiently detailed kinetics for the processes that determine the polydispersity in the additional dimensions. Such kinetics have been acquired for some problems described by the PBE such as crystallisation and aerosols, but are difficult to obtain for soot. Still, a multidimensional PBE has been used as the basis for the derivation of certain moment methods (Section 4.3.3).

4.2.2 Coagulation kernels

We now consider the form of the coagulation kernel, at first for spherical particles. The coagulation kernel, β(v,w), is the function describing the probability of coagulation of a particle of volume v with one of volume w. The forms of two important kernels used in soot modelling are shown below [55]. The first is the kernel for coagulation in the free molecule regime:

$$ \beta(v,w)=\left( \frac{3}{4 \pi} \right)^{\frac{1}{6}} \left( \frac{6kT}{\rho_{p}} \right)^{\frac{1}{2}} \left( \frac{1}{v}+\frac{1}{w}\right)^{\frac{1}{2}} \left( v^{\frac{1}{3}}+w^{\frac{1}{3}} \right)^{2} $$

(17)

and the second is the kernel for coagulation in the continuum regime due to Brownian motion:

$$ \beta(v,w) = \frac{2kT}{3\mu} \left( \frac{1}{v^{\frac{1}{3}}}+\frac{1}{w^{\frac{1}{3}}}\right) \left( v^{\frac{1}{3}}+w^{\frac{1}{3}} \right) $$

(18)

where k is the Boltzmann constant, μ is the gas viscosity. In the continuum-slip regime, the following modification of Eq. 18 can be used [62]:

$$ \beta(v,w) = \frac{2kT}{3\mu} \left( \frac{C(v)}{v^{\frac{1}{3}}}+\frac{C(w)}{w^{\frac{1}{3}}}\right) \left( v^{\frac{1}{3}}+w^{\frac{1}{3}} \right) $$

(19)

where

$$ C = 1 + 1.257 \frac{2\lambda}{d_{p}} $$

(20)

is the Cunningham correction factor for slip flow, and the numerical factor has been obtained via an experimental fit by Davies [63]. In the above formulas, ρ_p is the particle density and d_p is the particle diameter, while the gas mean free path, λ, can be estimated from kinetic theory, assuming a single component gas whose molecules act like rigid elastic spheres [55, 64]:

$$ \lambda = \frac{1}{\sqrt{2} \pi \sigma^{2} N_{m}} $$

(21)

where σ is the molecular diameter and N_m is the number of molecules per unit volume. The latter can be obtained from the ideal gas law:

$$ N_{m} = \frac{p}{kT} $$

(22)

The transition from the one regime to the other depends on the Knudsen number, Kn, defined as:

$$ Kn = \frac{2 \lambda}{d_{p}} $$

(23)

For Kn >> 1 the particles are smaller than the mean free path and behave like molecules, hence Eq. 17 must be employed. For Kn << 1 the continuum assumption is valid and coagulation occurs due to Brownian motion, as described by Eq. 18. An approach due to Fuchs [65], can be used for the transition regime. Other kernels (laminar shear, turbulent shear, sedimentation) are prevalent for larger particles where inertial effects are considerable, but are not relevant for the usual size range of soot particles.

4.2.3 Aggregate morphology

Small soot particles coagulate to form approximately spherical particles (up to about 50 nm). Larger primary particles collide to form fractal aggregates (Fig. 1). The shape of primary particles is retained during aggregation, although some gradual deformation due to sintering may occur. If fractal aggregates are present, they must be accounted for in the population balance.

Fractal aggregates can be assumed to be composed of nearly monodisperse primary particles of radius α_p0 and characterised by their fractal dimension, D_f [55]:

$$ N_{p} = A\left( \frac{R}{\alpha_{p0}}\right)^{D_{f}} $$

(24)

where N_p is the number of primary particles per aggregate, R is a characteristic radius such as the radius of gyration and A is a proportionality constant. The value of D_f can be determined from experiments or Monte Carlo simulations. For spherical particles it is 3, while typical values for soot are around 1.8 [66].

In terms of kinetics, the collision kernels must be modified to account for the fractal dimension; for example, in the continuum regime and for N_p >> 1000, the Brownian motion kernel is modified as follows [55]:

$$ \beta(v,w)= \frac{2kT}{3\mu} \left( \frac{1}{v^{\frac{1}{D_{f}}}}+\frac{1}{w^{\frac{1}{D_{f}}}}\right) \left( v^{\frac{1}{D_{f}}}+w^{\frac{1}{D_{f}}} \right) $$

(25)

Growth and oxidation rates are determined by the surface area, which depends on the volume and number of primary particles, and a correction may be applied to account for a degree of overlapping [67].

4.3 Solution of the PBE

The direct numerical solution of the large system of coupled non-linear ODEs that constitute the discrete PBE is possible but very expensive, especially if the PBE is to be coupled with flow, unless a very small size range is considered. By contrast, the continuous PBE is a single non-linear partial integro-differential equation, but its solution poses severe challenges. The literature on methods for solving the continuous PBE is very large, and a comprehensive review cannot be attempted here; on the other hand, only a few of the methods have been employed for soot modelling in turbulent flows. In the following we will present an introduction to the main approaches and discuss in more detail the ones that have been used for this purpose.

4.3.1 Analytical and similarity solutions

Analytical and similarity solutions of the PBE can be obtained only for a few special cases. Nevertheless, these solutions are important for validating and benchmarking numerical methods. The PBE for growth alone is a first-order hyperbolic equation and can be solved with the method of characteristics, while nucleation can enter as a boundary condition [56, 68]. Some analytical solutions for pure coagulation, mostly with simplified kernels and particular initial distributions, have been derived with the method of Laplace transforms, and reviews of those can be found in [54, 56, 57]. Similarity solutions originate in the work of Friedlander [69, 70] and have been reviewed in [54,55,56,57].

4.3.2 Monte Carlo methods

Monte Carlo methods proceed by constructing an ensemble of particles and subjecting them to random events for each process in the PBE at every time step, consistent with the rate of that process. The application of Monte Carlo methods to the PBE dates from the work of Spielman and Levenspiel [71] on droplet coalescence and re-dispersion, and a general review can be found in [56]. In the field of soot modelling, Kaplan and Gentry [72] employed the Monte Carlo method to study the fundamentals of aggregation, while Mitchell and Frenklach [73, 74] studied the transition from coagulation to aggregation. Balthasar and Kraft [75] developed an algorithm simulating nucleation, surface processes and coagulation in 1-D laminar premixed flames. The works of Balthasar and Frenklach [76] and Patterson and Kraft [77] focus on the prediction of soot morphology, while Raj et al. [78] used a Monte Carlo method to predict PAH growth.

Monte Carlo methods are very expensive computationally, because a large number of particles are needed to obtain convergence. For this reason, they have been employed mainly for kinetic investigations in ideal or partially-stirred reactors and 1-D laminar flames. As the focus of this review is on turbulent flames, they will not be discussed in detail here, but the interested reader is referred to the above references. One recent study [79], however, applied the Monte Carlo method to a DNS simulation of a turbulent flame, by selecting subsets from the ensemble of Lagrangian trajectories of fluid particles and performing the Monte Carlo simulation of soot formation along the selected trajectories.

4.3.3 Moment methods

Methods belonging to this family do not attempt to solve for the distribution, but rather aim to compute its moments. The k-th moment is defined as:

$$ m_{k} = \int\limits_{0}^{\infty} {v^{k} n(v )dv } $$

(26)

Physical meaning can be given to some low-order moments: the zeroth moment is the total number of particles, while the first moment represents the total particle volume. Thus a method that predicts the first two moments of the distribution yields the same information as a model that solves for soot number density and volume fraction. The main motivation for moment methods stems from the fact that the number of variables employed is minimal. On the other hand, the distribution is not being computed, and assumptions must be made for reconstructing it from the moments. A more important issue is the fact that the moment equations are unclosed, except for special cases. As a result, a wealth of approximate closure methods have been developed. The literature on moment methods is very extensive, and only the main ideas will be introduced here.

The earliest detailed exposition of the method of moments can be found in the work of Hulburt and Katz [80]. The PBE must first be transformed into a system of equations for the moments by multiplying with v^k and integrating:

$$ \begin{array}{@{}rcl@{}} && \int\limits_{0}^{\infty} v^{k} \frac{\partial }{\partial t} n(v) dv + \int\limits_{0}^{\infty} v^{k} \frac{\partial }{{\partial v }}(G(v) n(v)) dv = \int\limits_{0}^{\infty} v^{k} B \delta(v-v_{0}) dv \\ &&+ \int\limits_{0}^{\infty} v^{k} \frac{1}{2} {{\int}_{0}^{v}} \beta (w,v-w) n(w) n(v-w) dw dv - \int\limits_{0}^{\infty} v^{k} \int\limits_{0}^{\infty} \beta (v,w) n(v) n(w) dw dv\\ \end{array} $$

(27)

In general, it is not possible to obtain a closed system for K moments, unless the functions describing the surface processes and the coagulation kernel assume special forms. For example, for a PBE for nucleation and size-independent growth or shrinkage, G(v) = G₀, we obtain:

$$ \begin{array}{@{}rcl@{}} \frac{dm_{k}}{dt} - k G_{0} m_{k-1} &=& {v_{0}^{k}} B \hskip 3em k=1,...,K \end{array} $$

(28)

$$ \begin{array}{@{}rcl@{}} \frac{dm_{0}}{dt} &=& B \end{array} $$

(29)

In this case the system of equations is closed. However, the assumption of size-independent growth or shrinkage is unphysical for soot when a description in terms of particle volume is employed, because the surface processes depend on surface area and hence on the 2/3 power of volume. If a linear measure of particle size, such as particle diameter, is employed as the independent variable in the PBE, then constant growth or shrinkage rate implies proportionality to surface area. However, the use of particle volume as a dimension facilitates the description of coagulation and aggregation, because the volume is conserved in these processes. The integral terms arising from coagulation and aggregation pose a similar closure problem, which is readily seen by substituting the kernels in Eqs. 17, 18 into Eq. 27. A solution can be found for the discrete PBE and the constant kernel [81] but, for most other cases, the moment equations are unclosed and involve fractional moments.

Various approximate methods have been proposed to provide closure for the moment equations. The main underlying ideas involved are: a) series expansion of the number density, b) presuming the shape of the distribution, c) obtaining the fractional moments by interpolation, and d) approximating the moment integrals with numerical quadrature whose parameters are allowed to evolve in time.

The approach of series expansion originates in the work of Hulburt and co-workers [80, 82], who proposed expansion in orthogonal functions. This approach has also been shown to be related to the method of weighted residuals [83], where the distribution is approximated via global trial functions, but which has not found application to soot. Taylor series expansions were tried in early work on soot [29] but their applicability was found to be limited.

If the shape of the distribution can be presumed, the moments will be expressible in terms of a few parameters, and the presumed distribution will allow the evaluation of all terms. This approach is very effective in applications where there is evidence that the distribution adopts a well-known form—some examples are the Rosin-Rammler distribution which is often employed in sprays [84] and the log-normal and gamma distributions in aerosols [85, 86]. The log-normal distribution was also investigated in early soot studies (see [87] and references within). In sooting flames, however, the combination of surface processes, coagulation and aggregation, as well as the effect of spatial variation of precursors gives rise to considerable variability and sometimes even bimodal features to the distribution, so the assumption of a presumed shape is not adequate.

The method of obtaining unknown moments via interpolation was proposed particularly for soot and became the predominant method since the pioneering work of Frenklach and Harris [29], and was described as Method II in the original work but later named Method of Moments with Interpolative Closure (MOMIC). In this approach, the fractional moments that result from the moment transformation are approximated via logarithmic interpolation from the integral moments. The derivation must be carried out individually for each different kernel or surface growth/oxidation process. The approach was extended by Kazakov and Frenklach [88] to cover a wider range of coagulation regimes and to include aggregation, the latter being accomplished by considering the moments of a distribution over mass and number of primary particles per aggregate. More elaborate MOMIC models of aggregation were presented by Balthasar and Frenklach [76] and by Mueller et al. [89], the latter employing a volume-surface area description and forming the basis for the HMOM method that will be discussed below. A comprehensive description of MOMIC has been provided by Frenklach [90]. The method has been applied to 1-D premixed laminar flames [24, 25, 29, 88], to turbulent premixed flames via LES [91] and also to turbulent non-premixed flames via RANS [92] and LES [93].

Another family of methods originate in the Quadrature Method of Moments (QMOM) proposed by McGraw [94]. QMOM is based on the concept of Gaussian quadrature, where the distribution is regarded as the weight function and the remaining part of the integrand as the function to be integrated. For example, the growth integral is approximated as follows:

$$ \int\limits_{0}^{\infty} v^{k} G(v)n(v) dv \simeq \sum\limits_{i = 1}^{n} w_{i} {v_{i}^{k}} G(v_{i}) $$

(30)

The aim is to determine the quadrature parameters, w_i and v_i, so that all integrals involving the unknown distribution with the same parameters can be approximated. The moments themselves are approximated in the same way:

$$ \int\limits_{0}^{\infty} {n(v)v^{k} dv } \simeq \sum\limits_{i = 1}^{n} {w_{i} {v_{i}^{k}} } $$

(31)

QMOM proceeds via a two-stage process that consists of updating the moments and inverting a matrix to obtain the quadrature parameters. In the Direct Quadrature Method of Moments (DQMOM) [95], ODEs for the quadrature parameters themselves are derived. The main advantage of the DQMOM is that it provides a system of ODEs in terms of a closed set of parameters, thus making it more convenient for coupling with CFD. DQMOM found few applications to turbulent non-premixed flames [96, 97]. Blanquart and Pitsch [98] presented a DQMOM-based model that employs eight moments and a trivariate PBE in terms of volume, surface area and number of active sites, and applied it to laminar premixed and non-premixed flames.

QMOM and DQMOM are more general and pose fewer constraints on the distribution than MOMIC, but can result in numerical problems as the process updating the moments is ill-conditioned. The Hybrid Method of Moments (HMOM), due to Mueller et al. [99], is an evolution of MOMIC incorporating concepts from DQMOM. It is derived from a bivariate PBE in terms of volume and surface area, and aims at capturing bimodality in the distribution by using DQMOM for the spherical particles and MOMIC for the fractal aggregates. The original work demonstrated the method in 1-D premixed and non-premixed laminar flames; subsequent works combined it with LES and applied it to turbulent non-premixed flames [100,101,102] and to an aircraft combustor [103].

4.3.4 Discretisation methods

Discretisation methods are based on a discrete representation of the continuous distribution. Unlike the discrete PBE, where each bin in the distribution corresponds to one unit, a discretised continuous PBE divides the domain of the independent variable into intervals of possibly unequal size. This allows covering a particle volume domain ranging over several orders of magnitude with a small number of sections.

Several challenges are encountered in devising a successful discretisation method for the PBE, owing to its integro-differential and non-linear nature. The domain spans several orders of magnitude, with different processes occurring at different scales: nucleation, for example, is a localised source appearing at the lower end of the particle volume spectrum, while coagulation spreads the distribution towards larger volumes. Coagulation involves integral terms whose discretisation is non-local, i.e. includes contributions from the entire domain, thus requiring a large number of operations. It is also not straightforward to obtain a discretisation of the coagulation terms that is conservative with respect to the moments in an arbitrary non-uniform grid. Furthermore, the growth term gives the PBE the features of a first-order hyperbolic equation, which means that the solution may involve sharp fronts. Work over the last four decades has resulted in a number of solutions to these problems and a large number of methods can be found in the chemical engineering and aerosol literature, but very few of them have found their way to soot modelling so far.

One of the first approaches for the numerical solution of the PBE is the method of Gelbard et al. [104], proposed initially for coagulation and subsequently extended to multicomponent coagulation and growth [105]. It is based on approximating the distribution as a piecewise constant function (effectively a histogram) so that the evaluation of the coagulation integral terms involves products of number densities and numerical integrations of the kernel, and the latter can be precomputed for speed-up. Landgrebe and Pratsinis [106] developed a similar approach and employed it to study and map regimes of aerosol behaviour with respect to the time required to reach a self-preserving distribution. While these approaches were initially developed for atmospheric aerosols and nanoparticle synthesis, the Gelbard et al. method was later applied to model soot formation in laminar premixed flames [107], laminar counterflow diffusion flames [31, 108], laminar co-flow diffusion flames [32, 108,109,110,111,112]. The diffusion flame studies employed the PAH and nucleation kinetics by Hall et al. [31] (Sections 3.2 and 3.3).

A simpler approach adopted by a family of methods is to consider the distribution as a set of delta functions, each of which effectively represents a ‘bin’ of the discretised distribution. As a result, these methods do not carry out integrations of the kernel and number densities, but rather compute the coagulation source and sink terms pointwise. For example, the approximation of the source term integral for the bin $(v_{i}-\frac {\delta v_{i}}{2}, v_{i}+\frac {\delta v_{i}}{2})$ can be written as:

$$ {\int}_{v_{i}-\frac{\delta v_{i}}{2}}^{v_{i} +\frac{\delta v_{i}}{2}}{{\int}_{0}^{v}} \beta (w,v-w) n(w) n(v-w) dw dv \approx \sum\limits_{{\begin{array}{c} j \\ v_{k}+v_{j}=v_{i} \end{array}}} Q_{k,j} n_{k} n_{j} $$

(32)

where the factors Q_k,j include the kernel and any other correction factors required by the approximation scheme. An inherent problem in this approach is that the sum of volumes v_k + v_j will almost never be equal to the representative volume of any other interval unless a uniform grid is employed, so the resultant particle must be allocated to one of the two adjacent points and thus gain or lose volume. To counter this effect, correction factors (incorporated in Q_k,j) are introduced so as to conserve one or two moments of the distribution. Methods in this category are thus intermediate approaches that bridge the gap between moment and discretisation methods; they are fast and ensure moment conservation, possibly at the expense of accuracy in the prediction of the distribution. A number of these methods are based on a geometric grid, in which several simplifications are possible, particularly coagulation. For example, if v_i = 2v_i− 1, only particles from the previous point can contribute to the coagulation source term, a fact that greatly reduces the number of computations to be carried out. The geometric grid was first proposed by Bleck [113] and further developed by Marchal et al. [114] and Hounslow et al. [115]. The last of these methods conserves both number density and particle volume, but is still limited to a particular geometric grid.

The most general and flexible method in this class is that of Kumar and Ramkrishna [116, 117], which solves algebraic equations to compute correction factors that conserve any two moments of the distribution and is not tied to a particular choice of grid. While these methods were originally developed for different applications such as crystallisation, the Kumar and Ramkrishna method has been been adapted for use in soot modelling. Park and Rogak [118] employed it for the discretisation of the coagulation term, in conjunction with their method for discretisation of the growth term that will be discussed below, initially for modelling aerosol synthesis. Their overall approach was subsequently applied to soot modelling in several studies, including [119,120,121,122] in ideal reactors, [123,124,125,126,127] in laminar co-flow diffusion flames and [128] in laminar premixed flames.

An alternative to the approximation of the distribution by a piecewise constant function is to employ higher order trial functions via a finite element method. Gelbard and Seinfeld [129] employed cubic splines in their early work, but abandoned this approach in favour of the one described above [104]. Other finite element studies employed collocation and Galerkin methods [130, 131] or collocation with linear trial functions [132]. Netzell [133] developed a method that, while not derived via a finite element method, allows for variation of the distribution within each bin. This approach was used in a number of soot modelling studies on laminar [134, 135] and turbulent [136, 137] flames, a diesel spray confined in a high-pressure vessel [138] and a Diesel engine [139].

A recent approach by Liu and Rigopoulos [140] is based on a piecewise constant approximation of the distribution in the context of a finite volume scheme, applicable to an arbitrary grid. The resulting equations are akin to the formulation in [104, 106], which however employ geometric grids. The extension to an arbitrary grid, suggested in [106], involves many different cases for the boundaries of the double integrals approximating the coagulation integral terms. The method described in [140] identifies the boundaries for all cases in an arbitrary grid and results in a compilation of formulas for their geometric evaluation. As the boundaries are pre-computed, there is no overhead in the CPU time. The application of the method to soot formation was demonstrated via the simulation of a co-flow laminar flame, and it was shown that the CPU effort required for solving the PBE was less than 10% of the overall CFD simulation, thus demonstrating the potential for applying the method to turbulent flames.

The discretisation of the growth term poses a different computational problem: as it is a first order derivative, it can lead to sharp fronts. Early methods employed first order schemes that can exhibit considerable numerical diffusion. The concepts that have been employed to address this issue include: a) moving grids based on the method of characteristics, b) high resolution fixed grids that counter numerical diffusion, and c) adaptive grids.

In a moving grid approach, the nodes move to follow the growth process in a way guided by the method of characteristics. This is the basis of the method of Tsang and Brock [141], proposed for aerosols, and of Kumar and Ramkrishna [142], which combines the moving grid with their earlier sectional method for coagulation. In these methods, special care must be taken for the nucleation term which is always active at the lowest end of the volume range, an issue that can be addressed by adding nodes at that range [142]. Moving grid methods were applied to soot by Park et al. [120] and Wen et al. [121, 122]. A major issue with moving grids arises when the PBE is coupled with flow, as the distribution becomes spatially dependent and a different grid may be required at different locations.

Fixed grid approaches include high-resolution schemes that counter numerical diffusion with additional terms, as employed by Ma et al. [143] and Qamar et al. [144] for crystallisation. A related approach was developed by Park and Rogak [118], where a three-point fixed scheme is derived so as to conserve three moments and to reduce numerical diffusion. This method was developed for aerosols and used subsequently in soot modelling [119, 120].

Sewerin and Rigopoulos [145] developed an adaptive grid approach where the grid adaptivity is based on the gradient of the distribution, and combined it with a high resolution scheme. The method is based on a coordinate transformation between a reference uniform grid and an actual grid, and ensures that the nodes in the latter are distributed in an optimal way so as to capture accurately steep gradients. This method addresses the issue of coupling an adaptive grid with flow by discretising the PBE in a fixed reference grid, while the spatial variation of the grid is effected via additional transport terms. Finally, constraints are employed to ensure adequate resolution at the nucleation range. The method has been applied to the LES modelling of a turbulent sooting flame [146, 147].

The modelling of the morphology of aggregates via a discretised PBE can be carried out in several ways. In the earlier studies, only coagulation to spherical particles was considered. In some studies [119, 135,136,137, 148, 149], aggregates were considered via Eqs. 24 and 25, while a cut-off point was imposed for the transition between the smaller spherical particles and the larger fractal aggregates, with an interpolation between the kernels employed for the transition regime, in a manner similar to the approaches employed in moment methods. Care must be taken in estimating the surface of the aggregates; in [135, 137], this was done by fitting numerical results from the HMOM approach of [99].

A more comprehensive way, developed in the aerosol literature, is to employ a two-dimensional PBE in terms of volume and surface area [150, 151]. In this approach, the aggregate surface area is allowed to vary between the value corresponding to individual spherical particles touching each other up to that of a single spherical particle once complete coalescence has taken place. The method relies on a model for the sintering of the aggregate, which involves a characteristic sintering timescale that has been obtained for some nanoparticles. This approach is difficult to apply to soot, however, because it is difficult to obtain the required kinetic data.

Another detailed approach, also pioneered in the aerosol literature, is to employ two sets of discretised one-dimensional PBEs. Jeong and Choi [152] proposed the approach with PBEs for particle volume and surface area, and compared it with the two-dimensional PBE approach for silica and titania nanoparticles. Results showed that the approach was in good agreement with the two-dimensional PBE, while being considerably less expensive. Park and Rogak [153] developed a model based on one-dimensional PBEs for volume and number of primary particles per aggregate, also initially for aerosol synthesis. This model was subsequently applied to soot formation in a jet stirred reactor—plug flow reactor (JSR-PFR) combination by Park et al. [120], where no sintering was considered. A number of further studies employed this approach for the JSR-PFR system [121, 122] and laminar flames [125,126,127].

Finally, a different approach to the incorporation of a discretised PBE for soot modelling originates in the work of Pope and Howard [154] and is also related to the ‘method of classes’ developed by Marchal et al. [114] in crystallisation. In this method, the soot particle size distribution is also discretised into bins, each having constant number density or another property of the distribution such as mass or volume. The bins are then treated as chemical species and added to the reaction mechanism, while the growth and coagulation processes are represented as chemical reactions between bins or species such as C₂H₂ and PAH. The advantages of this approach include the seamless integration with the gas-phase mechanism and the ease of implementation, as the soot aerosol dynamics can be incorporated into a chemical mechanism implementation package such as CHEMKIN. However, this also implies that there is no flexibility for changing the grid once the PBE has been incorporated in the mechanism. Furthermore, treating the sections as species means that the PBE must be solved together with chemical kinetics, while the solution of the PBE as a separate equation can be carried out separately via operator splitting. This approach was further developed and applied to laminar premixed flames by Richter et al. [35], by D’Anna and co-workers to laminar non-premixed [42, 45] and premixed flames [41, 43, 44] and by Blacha et al. [155] to premixed and non-premixed laminar flames.

5 Coupling of Fluid and Aerosol Dynamics

The equations of aerosol dynamics in a spatially inhomogeneous flow field will now be considered. The governing equations of reacting flow are the Navier-Stokes, energy and species transport equations. The detailed formulation of these equations can be found in several sources, such as [156]; in this Section we will discuss how the PBE should be augmented to be coupled with flow.

The semi-empirical non-precursor and precursor models introduce only one or two additional scalar variables, hence the resulting transport equations are straightforward. For all other models the starting point is the PBE, which must now be augmented to account for spatial transport. The extra terms are convective transport, thermophoresis and particle diffusion. Including them in Eq. 16 results in the spatially distributed PBE (note that the number density is now a function of space and time, n(v,x,t), but the dependence on x,t is omitted for brevity):

$$ \begin{array}{@{}rcl@{}} &&\frac{\partial n}{\partial t} + \frac{\partial }{\partial x_{i}} \left[ (u_{i} + {u_{i}^{t}}) n \right]+ \frac{\partial}{\partial v} (G(v,\mathbf{y},n) \\ &&\qquad\qquad\qquad= B(\mathbf{y})\delta(v-v_{0}) + \frac{\partial}{\partial x_{i}} \left( D_{p} \frac{\partial n}{\partial x_{i}} \right) \\ &&\qquad+ \frac{1}{2} {{\int}_{0}^{v}} \beta (v-w,w) n(v-w) n(w) dw - {\int}_{0}^{\infty} \beta (v,w) n(v)n(w) dw \end{array} $$

(33)

where y is the concentration vector and ${u_{i}^{t}}$ is the thermophoretic velocity [55]. Equation 33 is coupled with the Navier-Stokes and scalar transport equations. Methods for the discretisation of the PBE can then be applied to derive a number of scalar transport equations for the discretised number densities, or moment methods can be applied to reduce it to a number of moment transport equations. For Monte Carlo methods, on the other hand, the coupling is more complex, as a Lagrangian stochastic particle simulation should be carried out to approximate the PBE, concurrently with the CFD simulation of the reacting flow. In Monte Carlo simulations of one-dimensional sooting laminar flames, the PBE is often applied as a post-processor after the steady-state solution of the flame has been obtained [75].

The majority of simulations of soot formation in laminar flows have been conducted on one-dimensional premixed or non-premixed flames, where the soot formation can be decoupled from the steady-state simulation of the flame. In many works, a temperature profile measured from experiments was imposed, thus removing the need for coupling soot and radiative heat transfer. In some of the earlier works, measured species profiles were also imposed. The experimental configurations investigated include burner stabilised flames, opposed jet flames and Wolfhard-Parker burners. While these approaches remove the need for coupling of soot and flow, the aim there was mainly to test and calibrate the soot models. As the focus of this review is on turbulent flames, a review of these works will not be attempted; the reviews focussing on soot kinetics, such as [5, 10], contain references to this literature.

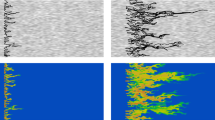
A configuration that requires full coupling of CFD, radiative heat transfer and soot formation in a laminar flame is the co-flow non-premixed burner, employed in the experiments of Santoro et al. [157, 158] on ethylene flames. This case is a good preparatory step for the simulation of turbulent flames and has been simulated in a number of studies (e.g. [124, 159]). With the combination of detailed models for both chemical kinetics and aerosol dynamics, good agreement can be obtained. Figure 3 shows some results from [140], where the original Santoro experiments were employed to demonstrate the applicability of the conservative finite volume PBE discretisation method to soot.

Fig. 3

Simulation of the Santoro et al. [157, 158] laminar co-flow non-premixed ethylene-air flame with the conservative finite volume PBE discretisation method [140]. Clockwise from top to bottom: a) representation of the computational domain, b) prediction of integrated soot volume fraction at different heights above burner with different PBE grids, c) temperature profile at the centreline, and d) radial temperature profiles at various cross-sections. Reprinted with permission from [140]

6 Soot and Turbulence

The coupling of a soot model with fluid flow adds another level of complexity, as various non-linear interactions between random variables must be accounted for. These include interactions between velocity and scalar fluctuations, turbulence-chemistry interaction, turbulence-radiation interaction and turbulence-soot interaction. The focus of this review is on the coupling of aerosol dynamics and flow, so we will concentrate on the turbulence-soot interaction; the other aspects will be discussed only briefly, as there are reviews covering that ground.

6.1 Overview of the closure problem for soot in turbulent flows

The correlations arising from fluctuations of velocity or velocity and scalars in convective transport are addressed via turbulence modelling (in RANS) or sub-grid modelling (in LES). RANS has been the basis of the studies of soot formation in turbulent flows until relatively recently. While reducing drastically the computational requirements for the calculation of the flow field, RANS also places severe demands on the turbulence-chemistry and turbulence-soot interaction models, as the fluctuations and non-linear interactions at all scales must be modelled. This also means that the soot model need not be comprehensive, but only commensurate with the level of detail of the overall simulation. RANS simulations have been conducted on laboratory flames, IC engine combustion chambers and gas turbine combustors. Most of the studies on laboratory flames have been conducted with k-𝜖 model variants, such as the standard k-𝜖 with a modification for the spreading rate (e.g. [160,161,162,163]). Engine studies have often employed the RNG k-𝜖 model (e.g. [139, 164,165,166]), while gas turbine studies have used the RNG k-𝜖 [167] or the realisable k-𝜖 model [168]. The turbulent transport of scalars has also received considerable attention in the combustion literature (see e.g. [156, 169,170,171] for a review of relevant works), but in soot studies it is usually addressed with a gradient transport hypothesis. LES studies of turbulent combustion with soot have appeared in the last decade, mostly on laboratory flames [91, 93, 100,101,102, 137, 146, 172, 173], but recently also on IC engines [164] and gas turbine combustors [103, 174]. Finally, there have been a few studies of sooting flames that use Direct Numerical Simulation (DNS) where no turbulence model is employed [175,176,177,178,179,180,181,182]. More details on these studies will be given in Section 6.2.

The problem of turbulence-chemistry interaction arises due to the non-linear nature of the chemical reaction source term, which is therefore unclosed under averaging (in RANS) or filtering (in LES) and involves unknown correlations between chemical species and temperature. Models for closure of this term are of central importance in turbulent combustion modelling and reviews can be found in [156, 169,170,171], among others. Since soot kinetics depend on the concentration of precursors, accurate modelling of both chemistry and turbulence-chemistry interaction are prerequisites for the successful prediction of soot in a turbulent flow. The vast majority of soot modelling studies in turbulent flows have been conducted in non-premixed flames, and this is reflected in the selection of methods employed. The first RANS studies employed models that assume infinitely fast chemistry [17, 18, 161, 183], as was customary in combustion modelling at that time. Later studies were based on the flamelet model [46, 49, 160] or CMC [163, 184]. The transported PDF approach has also been employed in RANS studies [92, 185, 186]. In the LES era, flamelet-based approaches have been predominant [100,101,102,103, 137, 187]. CMC [173, 174] and the Linear Eddy Model (LEM) have also been employed [91, 93], and, recently, the transported PDF approach via stochastic fields [146]. A detailed closure scheme for the turbulence-chemistry interaction is clearly warranted, but also renders the overall simulation more expensive. On the other hand, the generality afforded by the transported PDF method (it is not targeted to premixed or non-premixed flames) opens the way for application to partially premixed flames, as encountered in gas turbines.

The interaction between turbulence, chemistry and radiation also involves unclosed non-linear correlations between temperature and species. Reviews of models for radiative transfer in flows and turbulence-radiation interaction can be found in [188, 189]. The presence of soot introduces an additional correlation between soot and temperature. A number of works have focussed on the effect of radiation in turbulent sooting flames, including [46, 49, 160, 183, 190,191,192,193,194,195]. Radiation will not be discussed further here, and the reader may consult the above works for more details.

The main focus of this review will be on the interaction between turbulence and aerosol dynamics. Soot models include various non-linear functions involving both the soot variables and chemical species, and unclosed terms result from the averaging in RANS or filtering in LES context. The closure of these terms poses several unique problems that will be considered below.

6.2 Turbulence-soot interaction for monodisperse and moment-based models

In monodisperse soot models, soot is usually described in terms of two variables—soot number density and volume fraction. The transport equations for these quantities involve the concentrations of precursors and the temperature, and averaging or filtering of the equations results in unknown correlations involving fluctuations in species, temperature and soot variables. For example, the averaging of Eq. 1 in the semi-empirical non-precursor model of Moss et al. [19] yields:

$$ \frac{d}{dt} \left( \frac{\langle n \rangle}{N_{A}} \right) = \langle \alpha \rangle - \left\langle \beta \left( \frac{n}{N_{A}} \right)^{2} \right\rangle $$

(34)

In this model, α is a non-linear function of temperature and mixture fraction, and therefore averaging results in a closure problem similar to the reaction source term in combustion. The last term results in a non-linear correlation involving temperature (via the function β) and soot number density. The semi-empirical precursor-based models result in correlations involving species’ concentrations rather than mixture fraction. In most earlier studies, the effect of such correlations was omitted. However, several of the timescales involved in soot formation are slow and the need for accounting for these correlations has been acknowledged [46, 49].

In the early work of Magnussen et al. [17, 18], based on the eddy dissipation model, soot was introduced according to the Tesner et al. [16] model with the addition of oxidation, with adjusted parameters and no turbulence timescale for soot formation. The agreement with experimental results from C₂H₂ diffusion flames was quite good, but it must be borne in mind that this soot model does not predict the soot volume fraction, which was the variable compared with, so predictions were accomplished by assuming a mean particle size, different for each flame. Gore and Faeth [183] and Kent and Honnery [161] employed the conserved scalar approach, also based on the assumption of infinitely fast chemistry. In these two studies, the soot volume fraction was correlated with the mixture fraction based on experimental measurements in laminar [183] or turbulent [161] flames, hence effectively no soot modelling was employed. In the latter study, however, it was concluded that soot cannot be successfully modelled via a simple correlation with mixture fraction.

Several subsequent studies were based on a coupling of the flamelet method with monodisperse soot models, via solving differential equations for soot as a post-processor utilising the steady flamelet profiles. This approach was first proposed by Syed et al. [46], where the inability to resolve soot in a steady fashion was emphasised. The semi-empirical non-precursor soot model of Moss et al. [19] was used in that study, with the modification of having surface growth proportional to surface area. Experimental flamelet profiles were used for temperature and species, thus accounting for the soot-radiation interaction, although not in a fully predictive manner. Correlations involving the turbulent fluctuations of soot were not taken into account, and were identified as one of the plausible reasons for the lack of agreement with the experimental data. In an attempt to compensate for these effects, oxidation (not included in the original Moss et al. [19] model) was introduced according to the Nagle and Strickland-Constable [50] model, but with adjusted parameters. A flamelet approach was also employed by Fairweather et al. [160], where the species’ profiles for a steady flamelet were calculated via a global mechanism, while the soot was described by the acetylene-based two-equation model [39]. The correlations involving fluctuations of soot variables were again neglected. Radiative heat loss was taken into account by adjusting the temperatures and densities obtained from the laminar flame calculations so as to match peak values at turbulent flame experiments. The parameters of the soot oxidation model were again modified to obtain better agreement.

A first attempt to take into account the turbulence-soot interaction was made by Kollmann et al. [185], who employed a transported PDF approach for mixture fraction, enthalpy and soot volume fraction. This approach inherently accounts for the non-linear effects of fluctuations in soot volume fraction (the only soot parameter in that work). However, this early work was based on a very simplified one-equation soot model due to Kennedy et al. [20], which assumes constant number density. The choice of soot model was necessitated by the PDF method, which in those early days was too expensive and memory-intensive to be used with a model including more variables.

The work of Brookes and Moss [49] was one of the most comprehensive attempts to study the effect of turbulence on soot formation in the context of flamelet methods. In that work, it was acknowledged that the correlations between soot and chemical species are of key importance for modelling soot formation in turbulent flows. To study their effect, three approaches were compared. The first one was based on the assumption that soot is assumed to be uncorrelated with mixture fraction but correlated with species and temperature (the approach used in previous flamelet-based works). In this way, the effect of fluctuations on terms that depend on concentrations and temperature, such as the nucleation rate, is taken into account, at least within the confines of the flamelet approach (which assumes that species and temperature are correlated with mixture fraction and, in that work, on radiative heat loss). The second approach was to assume that soot is fully correlated with mixture fraction. This enabled accounting for correlations appearing in non-linear terms involving the soot variables, by averaging over the values of soot for every mixture fraction obtained from a laminar flame calculation and using the presumed β-PDF method. The third approach neglected all fluctuations and employed mean values. As expected, the last approach did not give satisfactory results. The correlated closure gave considerably better results than the uncorrelated one, especially as the latter required ad-hoc scaling of the oxidation rate.

Kronenburg et al. [184] employed the CMC method in conjunction with the Leung et al. [39] soot model. The use of the CMC has a similar effect to the correlated soot-mixture fraction closure in Brookes and Moss [49]. A major aspect of this work was the study of differential diffusion effects, which were found to yield a significant improvement. Yunardi et al. [163] used the same soot model and CMC, but with the extension to C₆H₆-based nucleation [40]. CMC was also employed by Bolla et al. [164] in conjunction with a two-equation soot model [39] for modelling an n-heptane spray under diesel engine conditions.

The vast majority of studies of soot formation in turbulent flames have been conducted on simple fuels, namely CH₄ or C₂H₄. Wen et al. [196], however, simulated a turbulent kerosene flame using a formulation similar to Brookes and Moss [49] for soot modelling. A PAH-based nucleation model, based on the simplified approach of Hall et al. [31] (see Section 3.2), was also employed in the context of the two-equation soot model and found to yield better results than the C₂H₂-based one. It was argued that the combustion of kerosene results in routes to soot nucleation that are not C₂H₂-based, due to the fact that kerosene already contains aromatics. It must be noted that a later study of a laminar flame with a kerosene surrogate fuel by Moss and Aksit [197] employed a conventional C₂H₂-based model, also in the context of the Brookes and Moss approach, and obtained reasonable results in the context of laminar flame simulations.

After the early work of Kollmann et al. [185], the transported PDF method was employed again in conjunction with two-equation soot models by Lindstedt and Louloudi [92] and by Aksit and Moss [190]. In the first work, a two-equation model [40] and the method of moments were compared, and the results were not very different. It was concluded that the more accurate modelling of the turbulence-chemistry interaction afforded by the transported PDF method was crucial. In the second work, employing the soot model of [49], the PDF approach was employed only for the mixture fraction and the two soot variables, while a flamelet method was used for the gas-phase reacting scalars. Finally, a recent work by Consalvi et al. [191] employed a two-equation model [40] in the context of a hybrid flamelet/PDF approach, where the flamelet was used for the turbulence-chemistry interaction while the PDF was employed for the mixture fraction, enthalpy defect and soot properties.

Moment methods pose a similar closure problem to the semi-empirical precursor-based models, as the averaging or filtering of the transport equations for the moments results in unclosed terms involving the species’ concentrations, temperature and moments. However, the use of moments allows a more detailed soot model to be employed, and usually such simulations employ detailed gas-phase chemistry as well. The works of Mauss and co-workers [198, 199] employed flamelet methods with detailed chemistry, PAH formation and HACA surface reaction models, while Pitsch et al. [200] applied a similar soot model to the modelling of a spray combustion chamber operated under Diesel engine conditions. Pitsch et al. [201] employed a detailed soot model in the context of an unsteady flamelet approach, including differential diffusion. Zamuner and Dupoirieux [186] first employed a transported PDF for the species and moments, together with a detailed soot model based on the HACA mechanism. Lindstedt and Louloudi [92] also employed the transported PDF for species and soot properties and compared an approach based on the Leung et al. [39] two-equation model and one based on the HACA mechanism and MOMIC [24].

LES studies of soot formation have taken over RANS during the last decade, and have been largely based on the same modelling principles employed in RANS for the subgrid contributions to the soot model. El-Asrag et al. [91] and El-Asrag and Menon [93] employed the Linear Eddy Model in LES (LEMLES) in conjunction with MOMIC. The subgrid model in LEMLES consists of solving a 1-D equation for diffusion, reaction and a convection term representing a ‘stirring’ process that emulates the effect of turbulence. The implementation of the soot model in this framework allowed accounting for the different diffusivities of soot and species. Navarro-Martinez and Rigopoulos [173] employed CMC in conjunction with LES and the the Leung et al. [39] two-equation model. CMC, like LEM, allows accounting for sub-grid differential diffusion and in this study it was found, as in [184], that including it improved the results.

Mueller and Pitsch [187] proposed an approach for subgrid modelling based on a presumed PDF approach for the turbulence-soot interaction that was used in several subsequent studies. In their approach, soot intermittency is explicitly taken into account by means of a double-delta PDF comprising a sooting and a non-sooting mode. Soot intermittency has been observed experimentally and can be attributed to the low diffusivity of soot particles, as well as to the sensitivity of PAH precursors to strain rate [187]. The subgrid intermittency, ω, was defined as follows:

$$ \omega = 1 - \frac{\overline{M}_{x,y}^{2}}{\overline{M_{x,y}^{2}}} $$

(35)

where M_x,y can be any second moment (as the approach is developed in conjunction with HMOM, the distribution is bivariate—see Section 4.3.3), and DNS simulation, due to Bisetti et al. [179], was used to evaluate the possible choices of moments. An additional transport equation for a second moment was required to compute ω, which involved an unclosed correlation between the moment and the divergence of the total velocity (defined as the sum of the fluid and thermophoretic velocity). This correlation was neglected, as comparison with DNS showed that the resulting error was small. The model was subsequently used in further studies [101, 102] in conjunction with the Radiation Flamelet/Progress Variable (RFPV) model [202], which extended the FPV model [203] to account for radiative heat transfer.

The DQMOM approach was also extended to LES, in conjunction with the RFPV model, by Xuan and Blanquart [204]. This study focussed on the turbulence-PAH chemistry interaction and concluded that its impact on soot yield is significant. Finally, soot modelling in LES has recently started to be applied to model combustors. Eberle et al. [172] employed LES but neglected turbulence-chemistry, turbulence-radiation and turbulence-soot interactions, together with a detailed PAH-based nucleation model and a simplified two-equation model for the remaining soot processes, while Giusti et al. [174] employed LES-CMC and a two-equation soot model [39].

Concurrently with the LES studies, a number of DNS studies were conducted. The first works, due to Lignell et al. [180, 181], were conducted with a monodisperse model, while the works of Bisetti and co-workers [175,176,177,178,179, 182] employed detailed kinetics and moment methods. Some the above studies have been used to inform and calibrate the LES subgrid models, such as the Mueller and Pitsch [187] model discussed above. Some DNS studies of coagulation of nanoparticles other than soot [205, 206] have also identified issues relating to the importance of small-scale particle-particle interactions that are relevant for soot particles. In DNS there is no modelling of soot-turbulence interaction, so these works will not be further discussed here.

6.3 Turbulence-soot interaction in the discretised PBE

The number of works that have employed a discretised PBE in turbulent flows is relatively small, but it has been growing in the recent years. While early adoption of the technique was limited by the constraints on computer memory, this is no no longer a major issue.

Flamelet-based discretised PBE approaches were initiated by the work of Netzell et al. [133, 136], who implemented a discretised PBE (their method was discussed in Section 4.3.4) in a RANS-based flamelet simulation of a turbulent jet flame. Fraioli et al. [165] applied the soot model of D’Anna and co-workers [41, 44] to the simulation of an IC engine using the eddy dissipation model. Aubagnac-Karkar et al. [134, 138, 139] applied the approach of Netzell et al. [133, 136] to the RANS modelling of IC engine combustion in conjunction with a tabulated chemistry model and kinetics for Diesel surrogate fuels. In these works, no further modelling of the coupling between turbulence and soot aerosol dynamics was attempted, other than the assumptions inherent in the eddy dissipation and flamelet models. However, they paved the way for the application of detailed aerosol models to practical combustion problems.

Rigopoulos [207] carried out a detailed study of the correlations that arise from the coupling of the PBE with turbulent flow. If the number density is split into a mean and a fluctuating part, as in a RANS simulation, then the ensemble averaging of the PBE gives rise to three kinds of unknown terms:

• 1. Correlation between reactive scalars (nucleation and growth/oxidation terms)

• 2. Correlation between reactive scalars and number density (growth/oxidation term)

• 3. Correlation between number densities (coagulation terms)

The correlations of type 1 are similar to those arising from the reaction source term in combustion and are accounted for partially or wholly depending on the turbulence-chemistry interaction model employed. The other two types, however, are unique to turbulent flows with aerosols. The correlations of type 2 arise because of the product Gn in the growth/oxidation term, while those of type 3 arise because the coagulation terms contain products of number densities, such as n(v − w)n(w). The existence of these terms had been identified earlier in the aerosol literature (see e.g. [54, 55]), but no method was available at the time to study them. A first study of these correlations was carried out in [207], where a PBE-PDF method based on the joint PDF of the reactive scalars and discretised number densities, f(y,n;x,t), was proposed. In this equation, all terms arising from turbulence-soot interaction appear in closed form. The PBE-PDF equation is:

$$ \begin{array}{@{}rcl@{}} && \frac{\partial}{\partial t} \left( \overline{\rho} \tilde{f} \right)+ \frac{\partial}{\partial x_{j}} \left( \overline{\rho} \tilde{u}_{j} \tilde{f} \right) +\frac{\partial }{\partial x_{j}}\left( \overline{\rho} {\left\langle {u_{j}^{\prime\prime}|\mathbf{Y}=\mathbf{y},\mathbf{N}=\mathbf{n}} \right\rangle \tilde{f}} \right) \\ &&= - \frac{\partial^{2}}{{\partial y_{\alpha} \partial y_{\alpha}}}\left( {\left\langle {\left. \overline{\rho} D_{\alpha} \frac{\partial Y_{\alpha}}{\partial x_{j}} \frac{\partial Y_{\alpha}}{\partial x_{j}} \right| \mathbf{Y}=\mathbf{y}} \right\rangle \tilde{f}} \right) - \frac{\partial^{2}}{{\partial n_{i} \partial n_{i}}}\left( {\left\langle {\left. \overline{\rho} D_{p} \frac{\partial n_{i}}{\partial x_{j}} \frac{\partial n_{i}}{\partial x_{j}} \right| \mathbf{N}=\mathbf{n}} \right\rangle \tilde{f}} \right) \\ &&- \frac{\partial}{\partial y_{\alpha} } (\overline{\rho} r_{\alpha}(\mathbf{y}) \tilde{f} ) - \frac{\partial}{\partial n_{i}} (\overline{\rho} B_{i} (\mathbf{y}) \tilde{f} ) - \frac{\partial }{\partial n_{i}} (\overline{\rho} {G_{i} (\mathbf{y},\mathbf{n}) \tilde{f}} ) - \frac{\partial}{\partial n_{i}} (\overline{\rho} C_{i} (\mathbf{n}) \tilde{f} ) \end{array} $$

(36)

where $\tilde {f}$ is the density (or Favre)—averaged pdf. The last three terms arise from the coupling of the PBE with fluid dynamics, while the remaining terms appear also in the joint scalar PDF equation for the species, including the chemical reaction source term, r_α(y). The expressions for the B_i, G_i, C_i terms, which arise from the nucleation, growth and coagulation terms respectively, can be found in [207]; the important feature of the method is that all of these terms appeared in closed form. The terms that still require closure are the turbulent transport, where a gradient transport model is typically applied, and the micromixing term, which represents the transport of the PDF in composition space due to diffusion and has so far been modelled via closures such as the Interaction with the Mean (IEM) [208, 209], though a modification is warranted to account for the lower diffusivity of soot particles.

Another issue with PDF methods in general is their high dimensionality, which rules out conventional discretisation approaches such as finite difference, because the CPU effort in these methods scales exponentially with the number of dimensions. Monte Carlo methods have been pioneered in turbulent combustion PDF methods, because the CPU effort in them (related mainly on the number of evaluations of the reaction kinetics and PBE) scales only linearly with the number of dimensions. Since the PDF is only a means for obtaining closure of the averaged reaction source term, its accurate calculation is not required. Three stochastic methods have been developed for PDF methods in turbulent combustion: the Eulerian particle [210], the Lagrangian particle [211] and the stochastic field method [212, 213]. The first of these methods is rather too restricted and no longer in use, but the other two methods have been adapted for the PBE-PDF method.

The PBE-PDF method was initially applied to a precipitation problem [214, 215] and to an aerosol problem [216]. In the first application to soot [217, 218], an acetylene-based soot model was employed and the coupling with CFD was accomplished via a RANS code and a Lagrangian stochastic particle method. A RANS approach was also employed by [148, 149], together with a more elaborate soot model based on HACA and incorporating coagulation. The flame simulated in that work, usually referred to as the Delft Flame III [219], is a CH₄-air flame that has been the focus of several other recent soot modelling studies [100, 102], although it has proved very difficult to obtain even qualitative agreement, partly because the soot kinetics of CH₄ is subject to greater uncertainty than that of C₂H₄, which is the focus of the majority of soot modelling studies.

Recently, the PBE-PDF was extended to LES by Sewerin and Rigopoulos [146, 147, 220], initially for aerosol formation in a constant density flow and subsequently for soot. These studies were performed with an adaptive grid PBE discretisation [145] (Section 4.3.4), while the soot kinetics were acetylene-based. The soot simulation was also applied to the Delft Flame III, and the results exhibited the same problems regarding the onset of soot. The main focus of these works, however, was on the formulation of the LES-PBE-PDF approach and the development of a methodology for obtaining numerical solution. The latter was accomplished via the stochastic field method, where an ensemble of fields is employed to represent the subgrid PBE-PDF, each having its own values of chemical species and discretised particle size distribution at every point in space. The approach is well suited to LES, largely due to avoiding the issues with particle tracking and control of the number of particles per cell. The IEM model was employed for closure of the micromixing term; while it is a simple model with known deficiencies, its impact is severely reduced in LES. Of particular note is the breakdown of CPU times: the discretised PBE required about 27% of the total CPU time per time step, indicating that its overhead is on par with the other main aspects of the computation and that the whole approach is thus feasible.

The flamelet-based discretised PBE approach was also extended to LES recently by Rodrigues et al. [137], where the RFPV [202] model was used as a basis, as in the HMOM-based LES studies [101, 102]. In that work, the PBE discretisation was along the lines of the Netzell et al. [133, 136] approach, while a detailed soot model including PAH chemistry, coagulation and aggregation was employed. The subgrid closure was accomplished by adapting the Mueller and Pitsch approach [187], originally formulated in the context of HMOM, to the discretised PBE. The subgrid intermittency (35) was defined in terms of the particle number density. As with all LES studies of sooting flames, quantitative agreement for the soot measurements could not be attained, but qualitative trends were reproduced.

6.4 Performance of soot models in turbulent flows

The quantitative modelling of soot formation in turbulent combustion lies beyond the frontier of current computational models. This has been evidenced by the four International Sooting Flame (ISF) Workshops that took place so far, and whose proceedings are freely available online [221]. In these workshops, a number of target flames were selected, for which experimental data were available. The flames were simulated by several groups with various aspects of the methods varying among the simulations, including the modelling of the flow field, turbulence-chemistry interaction and aerosol dynamics. Even in the latest workshop, where the transition to LES has been complete, there are large differences between the results and none the simulations can be regarded as quantitatively predictive, although some qualitative trends are being reproduced. The sensitivity of models to chemical parameters such as the surface reactivity in the HACA mechanism has also been found to be considerable. Even basic flame parameters, such as the flame temperature, are difficult to predict due to their complex dependency on soot and radiation, and it is hard to conclude whether better agreement overall, where partially accomplished, is due to a particular aspect of the model or to a fortuitous compensation of errors.

At the moment, it is hard to determine which are the dominant factors for this lack of quantitative agreement, but some remarks may be made. The transition from RANS to LES has resulted in quantitative predictions for many problems in turbulent combustion, but in the case of soot this has not been accomplished yet. This indicates that fundamental uncertainties in soot chemistry, aerosol dynamics and their interaction with turbulence must be addressed in conjunction with the better prediction of the flow structure afforded by LES. The fact that at least semi-quantitative agreement can be attained in laminar flames using the advances in mechanistic modelling of soot chemistry and aerosol dynamics over the last thirty years seems to suggest that the interaction of the above with turbulence may be the missing factor. At the same time, the more detailed soot mechanisms developed for laminar flows are too complex to be implemented effectively in turbulent flow simulations. To maintain the computational cost to reasonable levels, such mechanisms are usually implemented in the context of flamelet-based turbulence-chemistry interaction models, which introduce further assumptions. The more elaborate soot models are based on PAH chemistry, and uncertainties in PAH prediction due to either chemistry or turbulence-chemistry interaction modelling impact severely on soot prediction. However, advances in CPU power mean that more and more detailed chemistry can be afforded, and results from its application can be expected in the near future. Finally, the prediction of the particle size distribution with PBE discretisation methods has been employed successfully in laminar flames, but it has started to be applied only very recently to turbulent flames. Apart from the interest in the distribution per se, its correct prediction can be expected to improve the prediction of soot reaction rates due to the elimination of uncertainties in the estimation of surface area.

7 Conclusions and Outlook

Soot modelling is currently a final frontier in turbulent combustion modelling. RANS simulations in the past often required considerable adjustment of kinetics in order to obtain even order-of-magnitude agreement. Even with the transition to LES and more complex soot models, quantitative or even good qualitative prediction of an arbitrary turbulent sooting flame cannot be guaranteed. The main uncertainties are related to kinetics, aerosol dynamics and interactions of the above with turbulence.

Soot kinetics remain a major uncertainty. Nucleation is still poorly understood, and several pathways have been proposed. From the modelling perspective, the main dilemma is between acetylene-based and PAH-based models. The latter are without doubt more realistic, but PAH kinetics themselves exhibit considerable uncertainty and the transition from PAH to nascent soot is not well understood. One further drawback of PAH-based models is that they render the simulation very expensive, which is a major consideration for LES simulations of realistic configurations such as gas turbines. The type of fuel may also be important in the choice of nucleation model. The models for surface processes (growth and oxidation) are also subject to debate. While HACA is generally accepted as the elementary reaction mechanism for these processes, surface chemistry requires a description of the reactivity of the surface which is very difficult to introduce in a fundamental way without making the model very complicated and relying on further unknown parameters. Therefore a parameter is employed, whose model has been subject to various adjustment in different studies. These issues are very difficult to resolve, and while advances can be expected through better experiments and molecular simulations, progress in this area is likely to be slow.

Aerosol dynamics play an important role in soot modelling. The combined effect of nucleation, surface processes, coagulation to spherical particles and aggregation to particles of a fractal shape gives rise to complex and often bimodal particle size distributions, and presumed distributions (such as the log-normal), frequently employed in other aerosol problems, are insufficient in the general case. While the vast majority of turbulent combustion studies have been conducted with simplified models, laminar flame studies with detailed solution of the PBE via discretisation or Monte Carlo methods have demonstrated the important role played by aerosol dynamics. The introduction of the PBE to turbulent combustion was so far limited by memory rather than by CPU power, but with increased memory availability it can be expected that in the future it will find increasingly its way to turbulent flow simulations.

Soot reaction rates depend on the description of surface chemistry and the available surface area. With respect to the former, significant progress has been made in mechanistic modelling via the HACA mechanism, although a major uncertainty is still present regarding the surface reactivity. With respect to the latter, prediction of the particle size distribution will aid in eliminating assumptions, though a full account of particle morphology requires a two-dimensional PBE. While there are no mathematical issues with the formulation of such a model and numerical methods for its solution have been developed in other communities, it requires kinetics for processes that determine the distribution in terms of the additional dimensions (such as sintering kinetics). In the case of soot, there is already considerable uncertainty in the kinetics for the one-dimensional PBE. Two-equation PBE models represent an economic compromise with promise for the future.

The interaction of turbulence with chemical kinetics is a major issue in turbulent flames, and possibly even more so in sooting ones. DNS simulations have shown that PAH are very sensitive to small-scale fluctuations, so PAH-based nucleation and condensation models are going to be seriously affected. Therefore it seems that the use of more elaborate turbulent-chemistry interaction models will be unavoidable, together with good prediction of scalar transport with LES and sufficiently fine grids.

Differential diffusion has to be part of comprehensive soot simulations due to the low diffusivity of particles, as has been indicated by both modelling and DNS studies. In LES, the use of an Eulerian method allows consideration of differential diffusion at the grid level, while currently there is no universally accepted model for the subgrid closures, though there are several proposals in the context of different turbulence-chemistry interaction models.

As soot processes exhibit relatively slow timescales, the interaction of turbulence and soot is a crucial factor and it may be very difficult to associate soot with just a few variables. The use of PDF-level closures may therefore be essential for the coupling of soot with turbulence. Finally, turbulence-radiation interaction is also an important factor that has been the subject of very few investigations so far.

The current state of the art indicates that the coupling of detailed kinetics, transport phenomena, population balance and radiation models allows reasonably good predictions of soot in laminar flames, albeit mainly for simple fuels and with substantially more uncertainties in kinetics than in the case of laminar non-sooting flames (which can be predicted very well for fuels whose kinetics have been extensively investigated). The step to turbulent flames, however, presents enormous difficulties for soot prediction. Advances in experiments, fundamental soot models, turbulence-multiphysics interaction models and simulations that exploit the newly available CPU power are all expected to contribute to future progress. At the same time, the wealth of models currently available can provide at least partial solutions to the problems of industry, if used judiciously and with an emphasis on concentrating on the rate-controlling aspect of each problem.

Appendix: Derivation of the Continuous PBE

We start by writing a balance equation for the number of particles within a volume range dv (Fig. 2):

$$ \frac{\partial n(v,t)}{\partial t} dv = j_{in} - j_{out} + S $$

(37)

where j_in, j_out are the fluxes of particles in and out of dv via continuous increase or decrease of their volume, and S is the source term.

Let G be the rate of continuous change of particle volume, i.e. the velocity along the particle volume coordinate:

$$ G = \frac{dv}{dt} $$

(38)

In general, G is a function that depends on v—e.g. for soot surface processes it depends on the surface area, and therefore on the $\frac {2}{3}$ power of volume. The fluxes therefore are G(v)n(v) and G(v + dv)n(v + dv). We now have:

$$ \frac{\partial n(v,t)}{\partial t} dv = G(v) n(v) - G(v+dv) n(v+dv) + S $$

(39)

The processes of soot surface growth, condensation and oxidation can be considered to result in continuous changes in particle volume, as they involve addition or subtraction of units as small as an atom, and therefore much smaller than the volume of soot particles. The function G(v) is therefore yielded by their sum.

The source term includes the processes of nucleation and coagulation:

$$ S = S_{n} + S_{c} $$

(40)

The nucleation term can be expressed as a delta function, so that nuclei of a certain volume v₀ at a rate B are generated:

$$ S_{n} = B \delta(v-v_{0}) dv $$

(41)

To obtain an expression for the coagulation terms, we have to consider all combinations of particles leading to the creation or destruction of particles. In the discrete PBE, the contribution of coagulation is (14):

$$ \left( \frac{dN_{i}}{dt} \right)_{coag}= \frac{1}{2} \sum\limits_{j=1}^{i-1}\beta_{j,i-j}N_{j} N_{i-j} - \sum\limits_{j=1}^{\infty}\beta_{ij} N_{i} N_{j} $$

(42)

For a continuous volume range, we have:

$$ \begin{array}{@{}rcl@{}} N_{i} &=& n(v)dv \end{array} $$

(43)

$$ \begin{array}{@{}rcl@{}} \beta_{ij} &=& \beta (v,w) \end{array} $$

(44)

We therefore have:

$$ \begin{array}{@{}rcl@{}} S_{c} &=& \frac{1}{2} \sum\limits_{j=1}^{i-1} \beta (v_{j},v_{i}-v_{j}) n(v_{j}) n(v_{i}-v_{j}) dv_{j} d(v_{i}-v_{j}) \\ &&- \sum\limits_{j=1}^{\infty} \beta (v_{i},v_{j}) n(v_{i}) n(v_{j}) d v_{i} dv_{j} \end{array} $$

(45)

Taking the limit as $dv_{j} \rightarrow 0$ with dv_i being fixed, we obtain:

$$ S_{c} = \frac{1}{2} dv {{\int}_{0}^{v}} \beta (w,v-w) n(w) n(v-w) dw - dv {\int}_{0}^{\infty} \beta (v,w) n(v) n(w) dw $$

(46)

We now substitute the nucleation and coagulation terms in Eq. 39:

$$ \begin{array}{@{}rcl@{}} \frac{\partial n(v,t)}{\partial t}dv &=& G(v) n(v) - G(v+dv) n(v+dv) + B \delta(v-v_{0}) dv \\ &&+ \frac{1}{2} dv {{\int}_{0}^{v}} \beta (w,v-w) n(w) n(v-w) dw - dv {\int}_{0}^{\infty} \beta (v,w) n(v) n(w) dw\\ \end{array} $$

(47)

Dividing by dv, we obtain:

$$ \begin{array}{@{}rcl@{}} \frac{\partial n(v,t)}{\partial t}& =& \frac{G(v) n(v) - G(v+dv) n(v+dv)}{dv} + B \delta(v-v_{0})\\ &&+ \frac{1}{2} {{\int}_{0}^{v}} \beta (w,v-w) n(w) n(v-w) dw - {\int}_{0}^{\infty} \beta (v,w) n(v) n(w) dw \end{array} $$

(48)

Taking now the limit as $dv \rightarrow 0$, we obtain the continuous PBE for surface processes, nucleation and coagulation:

$$ \begin{array}{@{}rcl@{}} && \frac{\partial n(v,t)}{\partial t} + \frac{\partial (G(v)n(v,t))}{\partial v } = B \delta(v-v_{0}) \\ &&+ \frac{1}{2} {{\int}_{0}^{v}} \beta (w,v-w) n(w) n(v-w) dw - {\int}_{0}^{\infty} \beta (v,w) n(v) n(w) dw \end{array} $$

(49)