Filtered Reaction Rate Modelling in Moderate and High Karlovitz Number Flames: an a Priori Analysis

Abstract

Direct numerical simulations (DNS) of statistically planar flames at moderate and high Karlovitz number (Ka) have been used to perform an a priori evaluation of a presumed-PDF model approach for filtered reaction rate in the framework of large eddy simulation (LES) for different LES filter sizes. The model is statistical and uses a presumed shape, based here on a beta-distribution, for the sub-grid probability density function (PDF) of a reaction progress variable. Flamelet tabulation is used for the unfiltered reaction rate. It is known that presumed PDF with flamelet tabulation may lead to over-prediction of the modelled reaction rate. This is assessed in a methodical way using DNS of varying complexity, including single-step chemistry and complex methane/air chemistry at equivalence ratio 0.6. It is shown that the error is strongly related to the filter size. A correction function is proposed in this work which can reduce the error on the reaction rate modelling at low turbulence intensities by up to 50%, and which is obtained by imposing that the consumption speed based on the modelled reaction rate matches the exact one in the flamelet limit. A second analysis is also conducted to assess the accuracy of the flamelet assumption itself. This analysis is conducted for a wide range of Ka, from 6 to 4100. It is found that at high Ka this assumption is weaker as expected, however results improve with larger filter sizes due to the reduction of the scatter produced by the fluctuations of the exact reaction rate.

1 Introduction

Flow simulations of practical combustion devices are often based on the LES paradigm, as this methodology has the potential to be accurate and to capture unsteady phenomena at affordable computational effort. Since the LES equations are filtered in space, they contain unclosed terms, and further modelling is therefore required in respect to the Navier-Stokes equations from which they are derived. In flows with combustion one of the key terms to model is the filtered chemical reaction rate and this is the purpose of a combustion model. Combustion models for LES of premixed flames can be roughly classified by their main concepts [1] as either geometrical (such as level-set models [2, 3] and thickened flame models [4]), mixing-based (such as eddy dissipation concept [5], partially stirred reactors [6] and the linear eddy model [7]) or statistical (such as transported probability density function (PDF) models [8] and presumed-PDF models [9,10,11]). Some of these models are combined with a simplified description of the chemistry, realized through tabulation, such as the flamelet generated manifolds (FGM) method [12] and the flame prolongation of ILDM (FPI) method [13].

A central parameter for classifying regimes of premixed combustion is the Karlovitz number, Ka, which is defined as the ratio of a chemical time scale to the smallest turbulence (Kolmogorov) time scale. Most combustion models mentioned previously have been developed and validated for regimes where the chemical time scale is shorter than the turbulent one, which corresponds to a low Karlovitz number. Future combustion devices are however expected to involve more intense turbulence and/or leaner mixtures to improve their efficiencies and reduce emissions, and such conditions leads to combustion devices that operate at higher Karlovitz numbers. When the turbulent length scales are much smaller than the reaction layer thickness, it is expected that small vortices may enter the reaction zone, thereby disrupting the flame structure. Modelling of the high Karlovitz number flames can therefore be challenging and there is a need to explore which types of models, both detailed and simple, can be applied at the high-Ka regime.

It has been observed in a recent study [14] that the unfiltered chemical source term has large local fluctuations and thus is difficult to model with tabulation methods, while the filtered source term is more readily modelled as long as the filter is large enough (Δ ≥ δ_th). This implies that a tabulated chemistry approach based on flamelets can still be useful in the high Karlovitz number regimes of combustion. Moreover, it is suggested in [15] that tabulation can be improved by including effects of strain on the flamelet, an effect that is well understood for the RANS framework but not as well established for the LES framework [16, 17]. In [14] it was also noted that unstrained flamelet modelling can work for low and high Karlovitz number (Ka_δ < 0.1 or Ka_δ > 100) while at intermediate Ka the strain, curvature and differential diffusion effects can be important.

Thus, this work proposes to assess a presumed-PDF model within the framework of LES for various Karlovitz numbers. It is representative of a class of statistical models for premixed combustion that has been discussed and applied in many previous studies, mostly in the RANS framework where there is no filter scale involved, from early developments [9,10,11] to more recent works [12, 17,18,19,20,21,22].

The specific model discussed here assumes that the sub-grid PDF is a beta-distribution and that a single reaction progress variable is enough to describe the flame locally. The goal is to perform an a priori evaluation of a model for the reaction rate, in particular its dependence on the filter size and the Karlovitz number. For this purpose, a set of DNS premixed flames with increasing complexity are used: a one-dimensional laminar with complex chemistry, a turbulent flame with single-step chemistry and 5 different turbulent flames with complex chemistry at different Karlovitz numbers. This includes different Karlovitz numbers, from low values (around 6) to very high values, much higher than those typically investigated in the context of flamelet modelling.

First, the use of a presumed beta-PDF for the sub-grid distribution of the reaction progress variable and the accuracy of the resulting modelled reaction rate is investigated. The analysis is performed for two cases where the flamelet assumption can be eliminated. Based on the analysis of a filtered one-dimensional flame a correction factor is defined to impose a consistent consumption speed. Second, the flamelet assumption is assessed for high Ka conditions. Unfiltered flames with multi-step chemistry are used to quantify the error from the flamelet assumption. Finally, filtering is used to show how the combination of the two assumptions, presumed PDF and flamelet, depends on filter size and Ka and highlights the effect of the suggested correction factor.

2 Methodology

2.1 Filtering of the DNS data

In order to perform an a priori analysis of LES models on DNS data a filter operation has to be defined. In this work filtering is defined as a convolution with a Gaussian filter kernel. A filtered quantity is denoted by an over-bar, such as $\overline {\psi }$, and it is computed as

$$ \overline{\psi}({\mathbf{x}, t}) = \iiint\limits_{V} \psi(\mathbf{r}, t) G(\mathbf{x}-\mathbf{r};{\Delta}) \ \mathrm{d}\mathbf{r}, $$

(1)

where V is the computational domain and G(x;Δ) is a Gaussian filter kernel with filter width Δ. Conventionally the filter width is defined as Δ² = s²/12 where s² is the variance of the Gaussian distribution [23]. Favre filtered (density weighted) quantities are also needed. These are denoted by a tilde and are defined as $\widetilde {\psi }=\overline {\rho \psi }/\overline {\rho }$.

The convolution product in Eq. 1 is computed in wave space as $\widehat {\overline {\psi }}(\textbf {k})=\widehat {\psi }(\textbf {k})\widehat {G}(\textbf {k})$ by the use of a Fourier transform. Here, $\widehat {\ }$ denotes a Fourier transform coefficient and k is the wave number vector. This is done both to avoid the need to truncate the filter kernel in space but also because filtering in physical space can have a prohibitive computational cost. Filtering in physical space is a convolution product with computational cost N × M (where N and M are the number of grid points in the computational domain and the filter kernel, respectively) while filtering in wave space consists of a regular product and two Fourier transforms which has computational cost N log N. This difference is significant, especially for large filters where M ≈ N.

As the transform cannot be applied to data that is not periodic in all spatial dimensions and thus a mirrored copy of the data is attached in the non-periodic direction.

Note that the filtering operation defined by Eq. 1 is used only to compute localized filtered values representative of what would be obtained from a LES. This should not be confused with ensemble averaging (represented by time averaging in the case of statistically stationary systems) which is used to obtain statistics.

2.2 Presumed-PDF model for the reaction rate

In combustion, the progress of reaction from reactants to products can be described by a reaction progress variable, c. In the case of single-step chemistry c is solved directly, but in the case of multi-step chemistry, many possibilities exist for the definition of c. Here, c is defined as the normalized mass fraction of H₂O since this is one of the few species that can be found throughout the entire flame structure including preheat and post flame zones. c can thus be expressed as

$$ c(\mathbf{x}, t)=\frac{Y_{\mathrm{H2O}}(\mathbf{x}, t)-Y_{\mathrm{H2O},u}} {Y_{\mathrm{H2O},b}-Y_{\mathrm{H2O},u}}. $$

(2)

Subscripts u and b denote the unburnt and burnt states, respectively. The Favre filtered progress variable is then defined as $\tilde {c}=\overline {c\rho }/\overline {\rho }$ where the filtering operation is given by Eq. 1. The transport equation for the filtered progress variable, $\tilde {c}$, follows directly from the transport equation for $\widetilde {Y}_{\mathrm {H2O}}$ and is given by

$$ \frac{\partial \overline{\rho}\tilde{c}}{\partial t} + \nabla \cdot (\overline{\rho}\tilde{\textbf{u}} \tilde{c} ) = \overline{\mathcal{D}} - \nabla \cdot \left( \overline{ \rho \textbf{u} c } - \overline{\rho} \tilde{\textbf{u}} \tilde{c} \right) + \overline{\dot{\omega}}. $$

(3)

In Eq. 3, u is the velocity vector, ρ is the density, $\dot {\omega }$ is the chemical reaction rate and $\mathcal {D}$ is the diffusion term (the transport model and the definition of the progress variable are described in Section 3). The three terms on the right hand side represent molecular diffusion, sub-grid transport and chemical reaction, respectively. All three require further modelling and the focus here is on the reaction term.

The sub-grid PDF of the reaction progress variable is defined as [24]

$$ P(\sigma;\mathbf{x}, t) = \iiint\limits_{V} \delta(c(\mathbf{r}, t)-\sigma) G(\mathbf{x-r}) \ \mathrm{d}\mathbf{r}, $$

(4)

where G is the filter function, δ is the Dirac delta-function and the volume V includes the support of G which here taken to be the computational domain.

The presumed-PDF model to be evaluated is now formulated as

$$ \overline{\dot{\omega}}(\mathbf{x}, t) \approx {{\int}_{0}^{1}} \dot{\omega}(\sigma) P(\sigma; \mathbf{x}, t)\ \mathrm{d}\sigma \approx \overline{\rho}(\mathbf{x}, t) {{\int}_{0}^{1}} \frac{\dot{\omega}(\sigma)}{\rho(\sigma)} P_{\beta}(\sigma; \tilde{c}(\mathbf{x}, t),\sigma^{2}(\mathbf{x}, t))\ \mathrm{d}\sigma, $$

(5)

where $\sigma ^{2}=\widetilde {cc}-\tilde {c}\tilde {c}$ is the Favre sub-grid variance of c, and P_β is the presumed Favre-filtered sub-grid PDF. This model is based on the following two assumptions:

• (i) The functional form of the Favre-filtered sub-grid PDF is presumed to be a beta-distribution, parametrized by $\tilde {c}$ and σ². This is expressed as

  $$ P(\sigma;\mathbf{x}, t) \frac{\rho(\sigma)}{\overline{\rho}(\mathbf{x}, t)} \approx P_{\beta}(\sigma; \tilde{c}(\mathbf{x}, t),\sigma^{2}(\mathbf{x}, t)). $$

  and corresponds to the second step in Eq. 5.

• (ii) The unfiltered reaction rate is assumed to be a function of only c, that is, $\dot {\omega }(Y_{i},T)\approx \dot {\omega }(c)$. This corresponds to the first step in Eq. 5. The function $\dot {\omega }(c)$ is given by a separate calculation of a steady one-dimensional flame.

In Eq. 5, the last integral is a 1D integral in composition space which makes it possible to pre-compute and tabulate the integral as a function of $\tilde {c}$ and σ². It is this possibility to tabulate that makes this model computationally efficient. For the present study a table is constructed based on 300 linearly distributed points in both $\tilde {c}$ and σ². The resulting two-dimensional table is illustrated in Fig. 1, together with the reaction rate profile of the one-dimensional flame. In the set of flames considered in the present study, pressure, equivalence ratio and unburnt temperature, are constant. To be able to model flames where these parameters are not constant, additional dimensions have to be added to the table and corresponding sets of additional one-dimensional flames would have to be computed.

Fig. 1

Left: Modelled reaction rate, $\overline {\dot {\omega }}/\overline {\rho }$, as a function of $\tilde {c}$ and σ². Normalization is done using the peak values of the one-dimensional unfiltered flame. Right: Reaction rate as function of c in the one-dimensional flame

It should also be noted that there exists a method where the PDF is obtained by filtering of one-dimensional flames instead of using a beta-distribution [22]. This was recently investigated in [14] but since no significant improvement was reported over the beta-distribution for three-dimensional flames this method will not be pursued here.

To compute $\overline {\dot {\omega }}$, an additional model for the unknown sub-grid variance σ² needs to be supplied. In LES this can be done either by an algebraic expression or by solving a transport equation for σ² [25, 26]. In this work the focus is on the two assumptions (i) and (ii) mentioned above and the modelling of σ² is thus not considered. Assessing the modelling of σ² for high Ka flames will be the topic of a separate study. Instead, the exact value of σ² is extracted from DNS and used directly in Eq. 5.

2.3 Error and correlation

To quantify the model error, two different metrics will be used. The first one is the integrated error, denoted by E. It is defined as

$$ E= \left\langle \frac{ |\overline{\dot{\omega}}_{e}-\overline{\dot{\omega}}| }{ |\overline{\dot{\omega}}_{e}| } \right\rangle, $$

(6)

where the symbol $\dot {\omega }_{e}$ is introduced to denote the exact filtered reaction rate, obtained through a direct filtering of the fully resolved data, and 〈⋅〉 denotes time and space average to obtain statistics (not to be confused with the filtering). The index i runs over data points (computational cells) sampled uniformly in space and over time in a statistically stationary flame. The choice of this error metric is motivated by the fact that in finite volume methods, commonly used to discretise the Navier-Stokes equations, it is not omega itself but its integral over a cell volume that is used. Typical cell sizes are of the same order as Δ, and since Δ can be larger than δ_th the integrated error E becomes a relevant quantity in the LES, at least in the context of finite volume methods.

The second metric is the weighted Pearson correlation coefficient [27], r, which is based on weighted covariances and is defined as

$$ r= \frac{ \left\langle w (\overline{\dot{\omega}}_{e}-\langle\overline{\dot{\omega}_{e}}\rangle_{w}) (\overline{\dot{\omega}}-\langle\overline{\dot{\omega}}\rangle_{w}) \right\rangle} { \left\langle w (\overline{\dot{\omega}}_{e}-\langle\overline{\dot{\omega}_{e}}\rangle_{w})^{2}\right\rangle^{1/2} \left\langle w (\overline{\dot{\omega}}-\langle\overline{\dot{\omega}}\rangle_{w})^{2}\right\rangle^{1/2} }. $$

(7)

Here, 〈⋅〉_w denotes weighted averages and w is the weight. The weight is set equal to the reaction rate itself, $w=\overline {\dot {\omega }}$, and this choice is made to prevent the large non-reacting zones outside the flame from affecting r. This way, data points with large reaction rate will contribute more to r than points with low rate. Note that a high correlation can exist even if E is large.

2.4 Scaled model

It is commonly known (and will be seen in Section 4.2.1) that for a one-dimensional flame, Eq. 5 tends to over-predicts the filtered rate. This happens when the filter is large enough that σ² > 0 and comes from the fact that the presumed shape PDF is not able to exactly produce the right sub-grid distribution. As a result, the correct laminar flame speed is not guaranteed for σ² > 0. However, for a one-dimensional laminar flame the model can be improved by introducing a correction factor f defined as

$$ f({\Delta}) = \frac{ {\int}_{-\infty}^{\infty} \overline{\dot{\omega}}_{e}(Y_{i},T;{\Delta})\ \mathrm{d}x }{ {\int}_{-\infty}^{\infty} \overline{\dot{\omega}}(\tilde{c},\sigma^{2};{\Delta})\ \mathrm{d}x } $$

(8)

where $\overline {\dot {\omega }}_{e}$ is the exact rate evaluated for the one-dimensional flame and $\overline {\dot {\omega }}$ is the modelled rate as in Eq. 5. The scaled model is then obtained as $f \overline {\dot {\omega }}(\tilde {c},\sigma ^{2})$.

Under the flamelet assumption a three-dimensional flame is assumed to locally have the same structure as a one-dimensional flame. It is therefore motivated to compute the factor f a priori (using a one-dimensional flame) and store it for use when modelling three-dimensional flames. Also, since the f only depends on Δ, it can be pre-multiplied in the table and its use will thus add no extra computational cost to an LES.

The factor f is defined as in Eq. 8 to ensure that the following condition is respected:

$$ {\int}_{-\infty}^{\infty} \overline{\dot{\omega}}_{e}(x)\ \mathrm{d}x = {\int}_{-\infty}^{\infty} f\overline{\dot{\omega}}(x)\ \mathrm{d}x $$

(9)

Physically the correction corresponds to enforcing the correct consumption speed for a one-dimensional flame. Indeed, the inability of a presumed beta-distribution to produce the correct flame speed is a known problem [28]. Moreover, f increases with the filter size, Δ, which is an important characteristics as will be shown in Section 4.2. It should also be noted that, while the correction factor can reduce the error E, it does not affect the correlation r.

3 Numerics and DNS Data

The current study uses a DNS dataset of turbulent, statistically planar, premixed flames. The computational domain is a rectangular box in an inlet-outlet configuration, discretised on a uniform grid. A planar premixed flame is in the centre of the domain at time t = 0 and it propagates towards the inlet at t > 0. Periodic boundary conditions are imposed in the cross-stream directions and a convective outflow boundary condition is used at the outlet. On the inlet boundary, a constant value for temperature (T = 298 K) and species is imposed while a turbulent time-varying boundary condition is used for the velocity. An instantaneous picture of the c = 0.8 iso-surface is shown in Fig. 2 for each simulation at a random time instant within the statistically stationary state. The wrinkled and distorted shape of the flames can be seen and the variation of $\dot {\omega }$ along the flame surface is shown by the colour scale. For higher Ka the variations are generally larger, but not for case D which has no variations since $\dot {\omega }$ in this case only depends on c.

Fig. 2

Iso-surfaces of c = 0.8 for the different cases. The surfaces are coloured by the reaction rate of c. The laminar flame thickness δ_th is indicated in each figure. In the figures the inlet is on the left

Five of the cases, referred to as A1, A2, A3, B anc C, are lean methane-air flames at atmospheric pressure and temperature. These simulations use multi-step chemistry and include differential diffusion. The methane/air chemistry is modelled with the skeletal mechanism of Smooke and Giovangigli [29], which contains 16 species and 35 reactions. The equivalence ratio is 0.6. Transport properties, i.e. species diffusion coefficients, thermal conductivity, and viscosity, are mixture averaged based on the detailed properties for individual species obtained from the CHEMKIN thermodynamic database. Diffusion velocities of individual species are modelled using the Curtiss-Hirschfelder approximation. Note that case B has been analysed in a previous work [30].

The sixth case, referred to as case D, uses a single global reaction with an Arrhenius rate expressed as $\dot {\omega }=(1-c)^{1.6}/\tau _{0}\times \exp (-E_{a} T_{b}/T)$ where τ₀ = 5 × 10^− 10s^− 1 and E_a = 9, unity Lewis number and a Prandtl number of 0.3. These parameters were chosen to get a laminar flame speed and thickness comparable to the methane-air flames. Important parameters for all six cases are summarised in Table 1.

Table 1 Parameters for the simulated cases. L_y is the cross-stream domain height, L₁₁ the upstream integral length scale, h the grid spacing, δ_th the laminar thermal flame thickness, η the upstream Kolmogorov length scale, $u^{\prime }$ the upstream velocity fluctuation and S_L the laminar flame speed

3.1 Numerical methods and turbulence generation

During the simulation, to keep the flame near the centre of the domain, the mean inlet velocity u_in is adjusted to match the propagation speed of the flame front. A fluctuating velocity component u^′(y, z) is also added at the inlet boundary plane. This component is obtained by extracting a plane from a pre-generated turbulent velocity field. The pre-generated turbulence is also used to set the initial conditions. For this purpose, a homogeneous isotropic turbulence field is generated as follows: a flow field with desired turbulence intensity and length scale is synthesized in a fully periodic cubic box by sampling sine waves of suitable wave numbers and amplitudes. The flow in this box is then simulated until a statistically stationary state is reached, quantified by convergence of the energy spectrum, the energy dissipation rate and the integral length scale. During this simulation the turbulence intensity and length scale is maintained by low-wavenumber forcing.

The low-wavenumber forcing strategy works by injecting energy to low wavenumber modes through the addition of a source term in the momentum equation. In wave space for wavenumber κ the source term is

$$ \hat{\mathbf{f}}_{\kappa} (t) = \frac{ \rho\langle \varepsilon \rangle I^{R}_{\kappa \leq \kappa_{f}}}{2\rho_{u} k_{f}(t)} \hat{\mathbf{u}}_{\kappa}(t) $$

(10)

where ρ is the local density, ρ_u is the density of the unburned mixture, 〈ε〉 = 〈2νS_ijS_ij〉 is the space averaged dissipation rate of turbulent kinetic energy in the constant density case, ν is the viscosity, S_ij is the strain rate tensor, $\hat {\mathbf {u}}_{\kappa }$ is the Fourier transform of the velocity u and $k_{f}={\sum }_{|\kappa |\leq \kappa _{f}} \hat {\mathbf {u}}_{\kappa } \cdot \hat {\mathbf {u}}_{\kappa } /2$ is the kinetic energy contained in the set of modes with |κ|≤ κ_f. The largest forced wavenumber, κ_f, is 3 for case B and 1 for all other cases. The function $I^{R}_{\kappa \leq \kappa _{f}}$ is stochastic and for every time step it is set to 1 for a randomly selected wavenumber in the shell |κ|≤ κ_f and to 0 for all others. When used in a reacting flow simulation the density ratio ρ/ρ_u appearing in Eq. 10 is introduced to ensure a weaker forcing in the flame and post-flame regions, and the rate of energy injection is also capped to ensure that the target u^′ is not exceeded. Further details on this forcing method are given in [31, 32].

The DNS solver is based on the governing equations for conservation of mass, momentum, energy and chemical species at low Mach number discretized on a uniform Cartesian grid, see Yu et al. [33] for a detailed description and validation. A 5th order weighted essentially non-oscillatory (WENO) finite difference method is used for convective terms and a 6th order central difference scheme is used for all other terms. For time discretisation a second-order operator splitting scheme [34] is employed by performing integration of the chemical source terms between two half time-step integrations of the diffusion term. The integration of the diffusion term is further divided into smaller explicit steps to ensure stability and the overall time step is set to ensure that the CFL number remains smaller than 0.1. In cases with complex chemistry the chemical source terms are integrated using the stiff DVODE solver [35]. The variable coefficient Poisson equation for pressure difference is solved using a multigrid method [36].

3.2 Summary of cases

Dimensionless parameters given in Table 1 are defined as follows: Karlovitz number Ka = (u^′/S_L)^1.5(δ_th/L₁₁)^0.5, Damköhler number Da = L₁₁S_L/(δ_thu^′) and turbulent Reynolds number Re_t = u^′L₁₁/ν_u where u^′ is the root mean square velocity fluctuation, L₁₁ is the integral length scale, S_L is the laminar flame speed, δ_th = (T_b − T_u)/|∇T|_max is the laminar flame thermal thickness and ν_u is the viscosity. The Kolmogorov length scale is computed as (ν³/ε)^1/4 where ε is the dissipation rate of turbulent kinetic energy. All turbulence quantities used in Table 1 are evaluated in the homogeneous non-reactive turbulence field that was used to set the initial and boundary conditions.

For cases A1, A2 and A3 the intention is to investigate the dependency on Ka while maintaining the domain size constant. The only parameter that was changed between these cases is therefore the turbulence intensity u^′ resulting in Karlovitz numbers 6, 74 and 540. However, although the aim was to also keep the integral length scale constant in those cases, it was found by autocorrelation, L₁₁, to decrease with u^′ and as result the cases have somewhat different length scales as seen in Table 1. To provide a case with very high Ka, case B with Ka = 4100 from [30] is used. This case has the same set-up as cases A1-3 except for the forcing radius κ_f which is 3 instead of 1. To investigate if the integral length scale is an important parameter, case C is introduced. This case has the same Karlovitz number as A2 (Ka = 74) but a larger domain size giving a 2.4 times larger integral length scale. Case C is used to verify that trends observed for cases A1-3 and B are due the turbulence intensity and not due to the turbulent length scale. Finally, case D is introduced to provide a suitable test case for assumption (i). Therefore, case D was chosen to have a single-step reaction scheme and unity Lewis number, a set-up which ensures that assumption (ii) is always verified.

4 Results

The results section is organized as follows: in Section 4.1 the parametrization of $\overline {\dot {\omega }}$ as a function of $\tilde {c}$ and σ² is investigated. In Section 4.2 assumption (i) is evaluated, first for a steady one-dimensional flame and then for the simplified-chemistry case D. In Section 4.3 assumption (ii) is evaluated using unfiltered data from cases A1, A2, A3, B and C and finally, the combined effect of both assumptions is discussed in Section 4.4.

4.1 Filtering and parametrization of the reaction rate

Before investigating the model, the effect of the filter operation on the reaction rate is illustrated. Instantaneous pictures of the unfiltered reaction rate $\dot {\omega }$ from the DNS data is shown in Fig. 3 for all cases. As observed from the figure a local flamelet structure is not preserved everywhere for case B because of the appearance of holes and irregularities in the reaction layer. Some perturbations can also be seen for case A3 but in the other cases the reaction rate is not significantly perturbed.

Fig. 3

Instantaneous picture of the reaction rates $\dot {\omega }$ computed directly from DNS data for all cases. The unit of reaction rate is kg/m³/s

The model given by Eq. 5 gives the reaction rate as a function of the mean and variance of the reaction progress variable, $\overline {\dot {\omega }}=\overline {\dot {\omega }}(\tilde {c},\sigma ^{2})$. It is therefore appropriate to study how well the reaction rate is parametrized by $\tilde {c}$ and σ². Figure 4 shows scatter plots of $\overline {\dot {\omega }}$ as a function of $\tilde {c}$ and σ² where colours indicate the magnitude of the filtered reaction rate, and Fig. 5 shows the standard deviation of the doubly conditioned reaction rate $\langle \overline {\dot {\omega }}|c,\sigma ^{2}\rangle$. The standard deviation is normalized for clarity by the peak of the single conditional average, $\max \langle \overline {\dot {\omega }}|c\rangle$. The precise quantity shown in the figure is thus

$$ \frac{ \left\langle[ \overline{\dot{\omega}}- \langle \overline{\dot{\omega}} \mid \tilde{c}, \sigma^{2} \rangle ]^{2}\mid \tilde{c}, \sigma^{2} \right\rangle^{1/2} }{ \max\langle \overline{\dot{\omega}} \mid c \rangle } $$

(11)

Low values indicate that $\overline {\dot {\omega }}$ is parametrized well by $\tilde {c}$ and σ². The figures show the two representative cases A2 and B for the two normalized filter sizes Δ⁺ = Δ/δ_th = 1 and 3.5.

Fig. 4

Scatter plot of $\tilde {c}$ and its sub-grid variance σ² for cases A2 and B. The colour scale shows the value of filtered reaction rate $\overline {\dot {\omega }}$ (kg/m³/s)

Fig. 5

Standard deviation of the doubly conditioned reaction rate $\langle \overline {\dot {\omega }}|c,\sigma ^{2}\rangle$ for cases A2 and B at two different filter sizes. The standard deviation is normalized by $\max \langle \overline {\dot {\omega }}|c\rangle$

Both figures indicate that the parametrization works well for case A2 and for case B with filter size Δ⁺ = 3.5 since the normalized standard deviation is below 0.1 for the most part. For case B with Δ⁺ = 1, however, vastly different values of $\overline {\dot {\omega }}$ are sometimes found for the same values of $\tilde {c}$ and σ², and standard deviation as high as 0.15 are common for this condition in Fig. 5. For both cases the standard deviation is lower when the larger filter size is used indicating that correlation between model and DNS can be expected for large filters. Low standard deviation is necessary for the model to be accurate because the model provides only one value for each given combination of c and σ². For the high Karlovitz number, case B, the scatter is larger and thus the local and instantaneous value of the modelled reaction rate may be inaccurate.

At large filter sizes the local variations of the reaction rate are smoothed out as shown in Fig. 5. This suggests that a flamelet model with presumed PDF may perform satisfactorily at high Karlovitz numbers even if assumption (ii) does not strictly hold, as long as the filter size is sufficiently large. However, larger filter sizes introduce errors that also need to be investigated which will be done next.

4.2 Evaluation of assumption (i)

Assumption (i), which states that the sub-grid PDF is a beta-distribution, and its effect on $\overline {\dot {\omega }}$ are evaluated in this section. Two conditions are chosen for this purpose: a filtered steady one-dimensional flame with multi-step chemistry, and the filtered three-dimensional case D which uses single-step chemistry. Under these conditions, assumption (ii) is verified exactly because the reaction rate is only a function of c, thus providing clean test cases for assumption (i). The two conditions are complementary since case D contains turbulence effects while the one-dimensional flame contains multi-step chemistry effects.

4.2.1 One-dimensional steady flame

In this section Eq. 5 is evaluated for a laminar one-dimensional (1D) flame. For this case assumption (ii) holds exactly since c is a monotonic function of the spatial coordinate. The only source of error in the modelled filtered reaction rate is due to assumption (i), i.e. differences between the sub-grid PDF from DNS and the presumed beta-distribution.

Figure 6a shows the exact filtered reaction rate $\overline {\dot {\omega }}_{e}$ (lines) and the corresponding presumed-PDF model (symbols) for normalized filter sizes Δ⁺ ranging from 0.35 to 8. From the figure it is seen that the model captures the shape of the profiles at the different filter sizes but for filters with Δ⁺ > 1 the magnitude is over-predicted. The level of over-prediction can be reduced by using the correction factor f introduced by Eq. 8 which is shown as a function of Δ⁺ in Fig. 7a. The result after applying the correction factor f is shown in Fig. 6b where over-predication has been mitigated. Although the match is good (the maximum error is below 9% of $\dot {\omega }_{\max }$ and much less for the two largest filter sizes), the shape of the modelled rate profile for Δ⁺ = 1 (blue curve) does not entirely match the correct shape even after the correction factor has been applied, this is due to the restriction from a presumed shape PDF.

Fig. 6

Filtered reaction rate in a one-dimensional flame (lines). Symbols show the corresponding results obtained from the presumed-PDF model. In a the model is unscaled and in b it is scaled following Eq. 8

Fig. 7

a Correction factor computed from Eq. 8 using the 1D flame. b Error E and correlation r for a one-dimensional laminar flame. Filters range from 0.1 to 10 times the thermal flame thickness. Circles shows the unscaled model from Eq. 5 and triangles shows the scaled model

In Fig. 7b the integrated error E and weighted correlation coefficient r (defined in Eqs. 6 and 7, respectively) are shown as functions of Δ⁺. The error E is shown both with and without the correction factor applied to the modelled reaction rate (denoted by scaled and unscaled, respectively). Without correction factor, E is very high for Δ⁺ > 3, while with the correction factor, it is less than 20 %. Using the correction factor does not reduce the error all the way to zero because it does not affect the shape of the reaction rate profile, but only its magnitude. The error in the unscaled model increases monotonically with Δ while the correlation r has a minimum at Δ⁺ = 1.5. There is also a corresponding maximum in the error of the scaled model for this filter size so this represents the least favourable filter size for the model according to the metrics used. The source of the seen error has to do with the use of a presumed PDF as this is the only approximation that is employed. In principle the error cannot be entirely mitigated unless the actual sub-grid PDF is extracted and used in place of the beta-PDF.

The actual sub-grid PDFs of c computed for the filtered one-dimensional flame are presented in Fig. 8 for the point with $\tilde {c}=0.5$ and 0.7 at filter levels Δ⁺ = 0.35, 1.0 and 3.5, and compared with beta-PDFs obtained for the same c and σ². These values were selected as a representative locations where the filtered reaction rate is significant for all filter levels. The dashed lines show the beta-distributions and the solid lines show the corresponding distribution that results from applying the density weighted filter to the actual flame. For the one-dimensional case the sub-grid PDF in x-space is equal to the Favre filter and can be transformed to c-space via P(x)dx = P(c(x))dc since c is a monotonic function of x.

Fig. 8

Sub-grid probability density function of the reaction progress variable for different filter levels for the one-dimensional laminar flame. Solid lines show P(c) and dashed lines show the model beta-distribution P_β(c). (a) and (b) show $P(c\mid \widetilde {c}=0.5)$ and $P(c\mid \widetilde {c}=0.7)$, respectively

To quantify the match between the modelled PDF and the beta-distribution, the Kullback–Leibler (KL) divergence D(P||P_β) is computed and listed in Table 2 for all cases. The KL divergence is defined as [37]

$$ D(P||P_{\beta}) = {{\int}_{0}^{1}} P(\sigma) \ln\left( \frac{P(\sigma)}{P_{\beta}(\sigma)}\right) \mathrm{d}\sigma $$

(12)

where P is the PDF extracted from simulations and P_β is the presumed beta-distribution. In the table, the KL divergence is listed for $\tilde {c}=0.5$ and $\tilde {c}=0.7$. For the one-dimensional laminar flame (1D), the divergence increases with filter size indicating a worse match of the beta-PDF for larger filters.

Table 2 Kullback–Leibler divergence D(P||P_β) for all cases at $\tilde {c}=0.5$ and $\tilde {c}=0.7$

Overall, the beta-PDF reproduces reasonably well the trends of the filtered PDF, at least for filter sizes Δ⁺ ≤ 1. However, discrepancies between the two PDFs in the high reactivity range of c values might cause large errors in reaction rate estimations, as shown in Fig. 7b. In particular, at filter size Δ⁺ = 1, there is non-negligible error in the PDF which explains the discrepancy in the reaction rate profile in Fig. 6.

As was mentioned previously, the physical motivation for introducing the correction factor f is to make the model consistent by preserving the integrated reaction rate and thereby the consumption speed (c.f. Section 2.4). This leads to a decrease in E for the one-dimensional flame and the reduction is substantial for large Δ. This is relevant for finite volume methods as explained earlier and thus f may effectively reduce the over-prediction that can occur for Δ⁺ > 1. It is anticipated that the same sort of over-prediction will be prevalent also in three-dimensional wrinkled or turbulent flames. Applying the correction factor for such flames may also lead to error reduction and this will be explored in the next section.

4.2.2 Turbulent flame with simplified chemical kinetics

After having studied the one-dimensional flame the next step is to investigate the three-dimensional turbulent flame of case D. This case uses a simplified chemical model based on a single global reaction and unity Lewis number, and it has a Karlovitz number of 40. Simple linear relations exist between local species mass fractions and the temperature because of the absence of intermediate species and differential diffusion. Therefore, only one scalar transport equation needs to be solved, and this scalar is equivalent to a progress variable c. Thus, $\dot {\omega }$ can be expressed as a function of only c, meaning that assumption (ii) holds making case D suitable to study the accuracy of assumption (i) in three-dimensional filtered flames.

A one-dimensional laminar flame based on the simplified chemistry is first analysed in order to obtain the correction factor f. Analogous to Fig. 7 the factor f, error E and correlation coefficient r are shown in Fig. 9 for this laminar flame. The trends for all these quantities are qualitatively similar to those of the previously discussed complex chemistry laminar flame with, but there are some quantitative differences owing to the somewhat different flame structure.

Fig. 9

a Correction factor f and b error E and correlation coefficient r for a one-dimensional laminar flame with single-step chemistry. Error E is shown both for the unscaled model (circles) and the scaled model (triangles)

For the tree-dimensional case D the error and correlation are shown in Fig. 10a. When filter size is increased the error increases monotonously (both with and without correction factor) and the correlation r decreases. This means that the approximation of the PDF by a beta-distribution becomes worse as the filter size increases, in contrast to the one-dimensional case (Fig. 9) where the correlation is high also for large filters and the correction factor can effectively reduce the integrated error (see also the Kullback-Leibler divergence shown in Table 2). But still, for case D, the scale factor is found to reduce the error by up to 50%. A comparison of sub-grid PDFs from model and DNS is also shown in Fig. 10 for three filter sizes and conditioned on $\tilde {c}=0.5$. A reasonably good match is seen, although not quite as good as in the one-dimensional case. However, a good match of the average PDF does not guarantee a low error in the local $\overline {\dot {\omega }}$.

Fig. 10

a Error E and correlation coefficient r for case D. Error E is shown both for the unscaled model (circles) and the scaled model (triangles). b Comparison of PDFs from the model (dashed lines) and DNS (solid lines) for $\tilde {c}=0.5$ in case D

4.3 Evaluation of assumption (ii)

The previously observed behaviour that the error due to assumption (i) grows with Δ⁺ for a three-dimensional flame must occur also when multi-step chemistry is used, and likely also at higher Re and Ka numbers. However, at these conditions, errors due to assumption (ii) may be present and thus an assessment on this assumption is needed. Assumption (ii) states that the unfiltered reaction rate is a function of only the progress variable, $\dot {\omega }=\dot {\omega }(c)$. To provide a clean test case, conditions have to be chosen such that assumption (i) is satisfied exactly. Assumption (i) states that the sub-grid PDF is a beta-distribution, and the condition where this assumption is satisfied is Δ⁺ = 0. At this condition the sub-grid PDF (both modelled and exact) will collapse to a delta function. The progress-variable used for the methane/air flames is based on the mass fraction of H₂O.

The unfiltered raw data, $\dot {\omega }$, shows large differences between model and DNS in most cases. This is illustrated in Fig. 11 which shows the joint PDF of the exact and modelled reaction rate. Under these conditions of zero variance the model is just the reaction rate from the one-dimensional laminar flame at a given c. For the cases with lower Ka, cases A1, A2 and C, two branches can be seen in the figures. These are marked by “A” and “B” in Fig. 11a and they correspond to relatively low (0.6-0.8) and high (0.9) c-values, respectively. The two branches results from a shift of the reaction rate profile in the c-coordinate as will be discussed later. No such clear branches can be identified in cases A3 and B. In case B, which has the highest Ka, a particularly large spread is seen. Case D has no spread at all. In this case the model rate is equal to the exact rate and assumption (ii) is fulfilled exactly as discussed before, and the case is included here only for completeness.

Fig. 11

The colour scale shows the joint PDF of the exact (DNS) and modelled reaction rate for unfiltered data from all cases. To make the scatter more visible the colour scale is logarithmic, numbers indicate the exponent of 10

Quantitative measures of the accuracy of assumption (ii) are provided by the error E and the correlation coefficient r. These are listed in Table 3 for cases A1-3, B and C. Karlovitz numbers are also listed for reference. The two cases that have the same Ka, cases A2 and C, have nearly the same values of both E and r which confirms that the 2.4 times difference in integral length scale does not affect E and r.

Table 3 Error and correlation coefficient of the presumed-PDF model when applied to unfiltered data

As a function of Ka the error has a minimum for case A3 (Ka = 540). Similarly, the correlation coefficient has a maximum for the same case. The trend of decreasing error with increasing Ka that is seen for cases A1-3 and the particularly low error in case A3 is in agreement with the findings of [14] where the effects of strain and curvature were seen to be less important for Ka > 100. Cases A1 and A2 fall in the regime where strain and curvature may have an effect. For these cases, modelling based on unstrained flamelets may not be suitable. Flamelet modelling of low Ka flames is however a well-known subject and only a short discussion will be given here; the focus is rather on the high Ka flames.

In Fig. 12a–c the joint PDF of c and $\dot {\omega }-\dot {\omega }_{e}$ is shown for cases A1, A3 and B. The line shows the conditional average $\langle (\dot {\omega }-\dot {\omega }_{e})|c\rangle$. Relatively large errors can be seen, which is to be expected since the data is unfiltered. In the low Ka case A1 the difference between $\dot {\omega }$ and $\dot {\omega }_{e}$ is largest in the range 0.9 < c < 1, while in the high Ka case B large difference is found in a wider range of c. Figure 12d–i shows scatter plots of c and the exact rate $\dot {\omega }_{e}$, coloured by the local curvature and tangential strain rate. Curvature is defined as 0.5∇⋅n where the normal vector n = ∇c/|∇c| points toward the product side, so positive curvature means that the centre of curvature is on the reactant side. The lines in these figures show the model predicted rate. At Ka = 6 (case A1) there is a clear connection between curvature and reaction rate; for points with positive curvature the rate profile is shifted to the left and for points with negative curvature the profile is shifted to the right. At Ka = 540 (case A3) a distinction between points of opposite curvature can still be seen. It is known that curvature and strain does affect flame structure in the flamelet regime, as seen for case A1. A possible explanation for the high correlation r that is observed in case A3 can be the short turbulent time scale: the local curvature/strain changes rapidly and the flame structure does not have time to respond the same way as in the flamelet regime. At Ka = 4100 (case B) there is no relation between curvature/strain and reaction rate indicating that the time scale of changes in curvature/strain is so short that the flame has no time to respond to the rapidly changing curvature/strain. Similar observations were made in [38] where it was shown that the response of a flame to strain is reduced at low Da. The model error E seen in case B is larger than that of case A3 and cannot be explained by any correlation with local curvature and strain. It could be due to the larger level of turbulence which induces faster random perturbations on the flame structure.

Fig. 12

(a–c): Joint PDF of c and the difference between modelled and exact reaction rate $\dot {\omega }-\dot {\omega }_{e}$. The colour scale is logarithmic and the numbers give the exponent of 10. The black line shows the conditional average $\langle (\dot {\omega }-\dot {\omega }_{e})|c\rangle$. (d–i): Scatter plots of c and exact reaction rate. The colour scale shows mean curvature normalized by 1/δ_th in (d-f) and tangential strain rate normalized by S_L/δ_th. The black line shows the modelled reaction rate

To conclude, it seems that the model error E due to assumption (ii) as a function of Ka behaves as follows: For a one-dimensional (planar) flame, E is relatively small. When the flame becomes wrinkled (case A1 and A2), E increases due to the growing curvature effects. When high Karlovitz numbers are reached (case A3), E drops to a smaller value due to weaker influence of curvature on the reaction zone. Finally, at very high Karlovitz number (case B), E increases again which might be an effect of convection driven mixing.

4.4 Combined effect of both assumptions

The model is now evaluated for cases A1-3, B and C with non-zero filter size. When these flames are filtered, neither assumption (i) nor (ii) holds exactly and both can contribute to errors. Under these conditions it is not possible to discern how much of the error can be attributed to either assumption. The conclusions from previous sections can however provide an indication.

A direct comparison of modelled sub-grid PDFs and PDFs extracted from DNS are shown in Fig. 13 for cases A1, A2, A3 and B using three filter sizes and three values of $\tilde {c}$. Case C is not shown here since its PDFs are very similar to that of case A2. In Table 2, the match between the PDFs and beta-distribution is quantified by the Kullback-Leibler divergence. The match is generally better for higher Ka and smaller filter sizes. As seen in the figure, the error can sometimes be significant near the reaction region when Δ⁺ ≥ 1.

Fig. 13

Sub-grid probability density of c at selected values of the filtered progress variable $\tilde {c}$. Different cases and filter sizes are shown as indicated in the figure. Symbols show the PDF from DNS and lines show the model beta-distribution

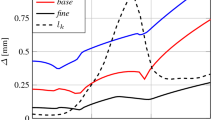
The mean error E and the correlation coefficient r are shown in Fig. 14 as functions of filter size for all three-dimensional cases. For most cases (A3 is the exception, as was discussed in the previous section) the correlation coefficient starts around 0.8 for the unfiltered flame, decreases to a minimum near Δ⁺ = 1 and then increases for larger filters.

Fig. 14

Error E and correlation coefficient r of the presumed-PDF model applied to a the filtered reaction rate of turbulent flames. Error E is shown both for the unscaled (circles) and scaled (triangles) versions of the model. Figures (a-e) shows cases A1, A2, A3, B, C and D, respectively

The error E for the scaled model generally decreases with filter size while the error of the unscaled model tends to have a minimum for some filter size Δ⁺ > 1, consistently with the observations from the one-dimensional flame in Section 4.2.1. The relatively large error and low correlation in the unfiltered flames is due only to assumption (ii), i.e. $\dot {\omega }$ is not well described by the one-dimensional flame as discussed in the previous section. When the Δ⁺ increases the effects responsible for the deviations from assumption (ii) are averaged over. The result of this is that the filtered field contains fewer deviations so that a larger filter helps improving the model predictions at high Ka. Furthermore, the sub-grid PDF is likely to be predicted with similar accuracy here as it was in the simplified-chemistry case D for which the correlation was always high (c.f. Fig. 10). Overall the non-monotonic error and correlation curves in Fig. 14 are consistent with a balance between the errors from the two assumptions that were previously discussed individually. Most of the error seen in these complex chemistry cases is however probably due to assumption (ii) which is related to the presence of intermediate species, curvature and strain. It is also noted that the correction factor f is effective in reducing the error also when the two assumptions are combined.

Cases A2 and C again have nearly identical values of E and r. Since these two cases only differ by their integral length scale it can be concluded that E and r do not have a major dependence on this parameter.

5 Conclusions

DNS data of premixed flames, both with single-step reaction and complex methane/air chemistry, at high Karlovitz numbers have been used for a priori evaluation of a presumed-PDF combustion model with flamelet tabulation. Filtered reaction rates of a reaction progress variable were computed from the model and compared with the corresponding rates obtained by direct filtering of DNS data. The main conclusions are summarized in the following:

• For flames with complex transport and chemistry the presumed-PDF model works better for large filter sizes than for small ones. For such flames most of the error stems from assumption (ii), i.e. the representation of the local rates by a flamelet through $\dot {\omega }=\dot {\omega }(c)$, and is therefore tied to the complex chemistry. The error at small filter sizes, however, is found to have a minimum for the case with Ka = 540 and larger error is seen for both larger (4100) and smaller (6 and 74) Ka. At low Ka this is believed to be due to the strong correlation observed between curvature/strain and shift in the reaction rate profile in the reaction progress variable coordinate. This correlation disappears for very high Ka.

• At high Karlovitz numbers a large filter has a smoothing effect which helps reduce the error from the flamelet assumption. This is an interesting behaviour for example for LES of gas turbines, where filter sizes can be relatively large compared to the flame thickness. The match between sub-grid probability distribution and the beta-distribution varies from acceptable to rather poor depending on the Karlovitz number, filter size and location in the flame. The corresponding error in the filtered rate increases with filter size which can be problematic for practical LES where the filter size cannot be too small for the computation to remain affordable. This was established by studying a flame with simplified chemistry where the flamelet assumption holds. For flames with complex chemistry and transport, this error seems to be small compared with the one from the flamelet assumption.

• A filter size dependent scaling factor for the model was defined using a filtered one-dimensional flame. The factor ensures that the flame speed is unaffected by filtering for the one-dimensional flame. This factor results in a substantial reduction of the model error for filter sizes larger than the thermal flame thickness, which is relevant for practical LES. The same factor can be used in three-dimensional flames which makes it inexpensive to use in LES since the factor can be pre-computed and stored.

This work has been concerned only with the flamelet assumption and the presumed PDF. When used in practical LES, the result will also be influenced by the choice of model for the sub-grid variance. Future follow-up studies should therefore contain both a priori analysis of models for the sub-grid variance and a posteriori analysis where a complete LES is performed with the proposed model.