A robust formulation for twin multiclass support vector machine

Abstract

Multiclass classification is an important task in pattern analysis since numerous algorithms have been devised to predict nominal variables with multiple levels accurately. In this paper, a novel support vector machine method for twin multiclass classification is presented. The main contribution is the use of second-order cone programming as a robust setting for twin multiclass classification, in which the training patterns are represented by ellipsoids instead of reduced convex hulls. A linear formulation is derived first, while the kernel-based method is also constructed for nonlinear classification. Experiments on benchmark multiclass datasets demonstrate the virtues in terms of predictive performance of our approach.

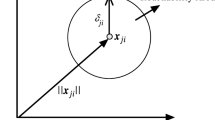
Appendix: Dual formulation of Twin-KSOCP and geometric interpretation

1.1 Proof of Proposition 1

The Lagrangian function associated with Problem (16) is given by

$$\begin{array}{@{}rcl@{}} L(\mathbf{w}_{1},b_{1},\lambda_{1},\lambda_{2})&=&\frac{1}{2}\left\| A\mathbf{w}_{1}+\mathbf{e}_{1}b_{1} \right\|^{2}+\frac{\theta_{1}}{2}(\|\mathbf{w}_{1}\|^{2}+{b_{1}^{2}})\\ &&+\lambda_{1}(\mathbf{w}_{1}^{\top} {\boldsymbol{\mu}}_{2}+b_{1}+1+\kappa_{1}\|S_{2}^{\top}\mathbf{w}_{1}\|)\\ &&+\lambda_{2}(\mathbf{w}_{1}^{\top} {\boldsymbol{\mu}}_{3}\,+\,b_{1}\,+\,1\!-\epsilon\,+\,\kappa_{2}\|S_{3}^{\top}\mathbf{w}_{1}\|), \end{array} $$

where λ ₁, λ ₂ ≥ 0. Since ∥v∥ = max ∥u∥≤1u ^⊤ v holds for any v ∈R ⁿ, we can rewrite the Lagrangian as follows:

$$\begin{array}{@{}rcl@{}} L(\mathbf{w}_{1},b_{1},\lambda_{1},\lambda_{2})&=&\max_{\mathbf{u}}\{L_{1}(\mathbf{w}_{1},b_{1},\lambda_{1},\lambda_{2},\mathbf{u}_{1},\mathbf{u}_{2}):\|\mathbf{u}_{i}\|\\&\le& 1,\ i=1,2\}, \end{array} $$

with L ₁ given by

$$ \begin{array}{llllll} L_{1}(\mathbf{w}_{1},b_{1},\lambda_{1},\lambda_{2},\mathbf{u}_{1},\mathbf{u}_{2})=\frac{1}{2}\left\| A\mathbf{w}_{1}\!+\mathbf{e}_{1}b_{1} \right\|^{2}+\frac{\theta_{1}}{2}(\|\mathbf{w}_{1}\|^{2}+{b_{1}^{2}})\\+\lambda_{1}(\mathbf{w}_{1}^{\top} {\boldsymbol{\mu}}_{2}+b_{1}+1+\kappa_{1}\mathbf{w}_{1}^{\top} S_{2}\mathbf{u}_{1})\\ +\lambda_{2}(\mathbf{w}_{1}^{\top} {\boldsymbol{\mu}}_{3}+b_{1}\!+1\!-\epsilon+\kappa_{2}\mathbf{w}_{1}^{\top} S_{3}\mathbf{u}_{2}) . \end{array} $$

(A.30)

Thus, Problem (16) can be equivalently written as

$$\begin{array}{@{}rcl@{}} \min_{\mathbf{w}_{1},b_{1} }\max_{\mathbf{u}_{1},\mathbf{u}_{2},\lambda_{1},\lambda_{2}}\{L_{1}(\mathbf{w}_{1},b_{1},\lambda_{1},\lambda_{2},\mathbf{u}_{1},\mathbf{u}_{2}):\|\mathbf{u}_{i}\|\\\le 1,\lambda_{i}\ge0,\, i=1,2\}. \end{array} $$

Hence, the dual problem of (16) is given by

$$\begin{array}{@{}rcl@{}} \max_{\mathbf{u}_{1},\mathbf{u}_{2},\lambda_{1},\lambda_{2}}\min_{\mathbf{w}_{1},b_{1} }\{L_{1}(\mathbf{w}_{1},b_{1},\lambda_{1},\lambda_{2},\mathbf{u}_{1},\mathbf{u}_{2}):\|\mathbf{u}_{i}\|\\\le 1,\lambda_{i}\ge0,\, i=1,2\}. \end{array} $$

(A.31)

The above expression allows the construction of the dual formulation. A detailed description of this procedure can be found in [26]. The computation of the first order condition for the inner optimization task (the minimization problem) yields to

$$\begin{array}{@{}rcl@{}} \nabla_{\mathbf{w}_{1}}L_{1}\!&=&\!A^{\top}(A\mathbf{w}_{1}\,+\,\mathbf{e}_{1}b_{1})\,+\,\theta_{1}\mathbf{w}_{1}\!\,+\,\lambda_{1}({\boldsymbol{\mu}}_{2}\,+\,\kappa_{1} S_{2}\mathbf{u}_{1})\\&&+\lambda_{2}({\boldsymbol{\mu}}_{3}\,+\,\kappa_{2} S_{3}\mathbf{u}_{2})\,=\,0,\qquad \end{array} $$

(A.32)

$$\begin{array}{@{}rcl@{}} \nabla_{b_{1}}L_{1}\!&=&\!\mathbf{e}_{1}^{\top}(A\mathbf{w}_{1}+\mathbf{e}_{1}b_{1})+\theta_{1}b_{1}+\lambda_{1}+\lambda_{2}=0. \end{array} $$

(A.33)

Let us denote by $\hat {\mathbf {z}}_{1}=[\mathbf {z}_{1};1],\, \hat {\mathbf {z}}_{2}=[\mathbf {z}_{2};1]\in \Re ^{n+1},$ with z ₁ = μ ₂ + κ ₁ S ₂ u ₁ ∈R ⁿ, and z ₂ = μ ₃ + κ ₂ S ₃ u ₂ ∈R ⁿ. Then the relations (A.32)–(A.33) can be written compactly as

$$(H^{\top} H+\theta_{1}I) \mathbf{v}_{1}+\lambda_{1}\hat{\mathbf{z}}_{1}+\lambda_{2}\hat{\mathbf{z}}_{2}=0, $$

where v ₁ = [w ₁; b ₁] and H = [A e ₁]. Since the symmetric matrix $\hat {H}=H^{\top } H+\theta _{1}I \in \Re ^{n+1\times n+1}$ is positive definite, for any 𝜃 ₁ > 0, the following relation can be obtained:

$$ \mathbf{v}_{1}=-\hat{H}^{-1}(\lambda_{1}\hat{\mathbf{z}}_{1}+\lambda_{2}\hat{\mathbf{z}}_{2}). $$

(A.34)

Then, by replacing (A.32)–(A.33) in (A.30), and using the relations (18) and (A.34), the dual problem can be stated as follows:

$$ \begin{array}{llllll} \max_{\mathbf{z}_{i},\mathbf{u}_{i},\lambda_{i} } & \ \lambda_{1}+\lambda_{2}(1-\epsilon)-\frac{1}{2}(\lambda_{1}\hat{\mathbf{z}}_{1}+\lambda_{2}\hat{\mathbf{z}}_{2})^{\top} \hat{H}^{-1}(\lambda_{1}\hat{\mathbf{z}}_{1}+\lambda_{2}\hat{\mathbf{z}}_{2}) \\ \text{s.t.}\, &\, \mathbf{z}_{1}= {\boldsymbol{\mu}}_{2}+\kappa_{1} S_{2}\mathbf{u}_{1}, \ \|\mathbf{u}_{1}\|\le1, \\ &\, \mathbf{z}_{2}= {\boldsymbol{\mu}}_{3}+\kappa_{2} S_{3}\mathbf{u}_{2}, \ \|\mathbf{u}_{2}\|\le1, \\ &\, \lambda_{1},\lambda_{2}\ge0. \end{array} $$

(A.35)

Notice that the Hessian of the objective function of the above problem with respect to λ = [λ ₁; λ ₂] ∈R ² is given by

$${H_{z}}=\left( \begin{array}{cc} \hat{\mathbf{z}}_{1}^{\top}\hat{H}^{-1}\hat{\mathbf{z}}_{1}&\hat{\mathbf{z}}_{1}^{\top}\hat{H}^{-1}\hat{\mathbf{z}}_{2} \\ \hat{\mathbf{z}}_{1}^{\top}\hat{H}^{-1}\hat{\mathbf{z}}_{2}& \hat{\mathbf{z}}_{2}^{\top}\hat{H}^{-1}\hat{\mathbf{z}}_{2} \end{array}\right). $$

Clearly, this matrix is symmetric positive definite. Then, the objective function of the dual problem (A.35) is strictly concave with respect to λ, and it attains its maximum value at the solution of the following linear system:

$$H_{z}\left( \begin{array}{c} \lambda_{1}^{*}\\ \lambda_{2}^{*} \end{array}\right)=\left( \begin{array}{c} 1\\ 1-\epsilon \end{array}\right). $$

This linear system has the following solution:

$$\begin{array}{@{}rcl@{}} \lambda_{1}^{*}&=&\frac{\hat{\mathbf{z}}_{2}^{\top}\hat{H}^{-1}\hat{\mathbf{z}}_{2}-(1-\epsilon)\hat{\mathbf{z}}_{1}^{\top}\hat{H}^{-1}\hat{\mathbf{z}}_{2}}{\det(H_{z})}, \\\ \lambda_{2}^{*}&=&\frac{(1-\epsilon)\hat{\mathbf{z}}_{1}^{\top}\hat{H}^{-1}\hat{\mathbf{z}}_{1}-\hat{\mathbf{z}}_{1}^{\top}\hat{H}^{-1}\hat{\mathbf{z}}_{2}}{\det(H_{z})}. \end{array} $$

(A.36)

Thus, the optimal value of Problem (A.35) (with respect to λ) is given by

$$ \frac{1}{2}(1\quad 1-\epsilon)(H_{z})^{-1} \left( \begin{array}{c} 1\\ 1-\epsilon \end{array}\right), $$

(A.37)

where

$$(H_{z})^{-1}=\frac{1}{\det(H_{z})}\left( \begin{array}{cc} \hat{\mathbf{z}}_{2}^{\top}\hat{H}^{-1}\hat{\mathbf{z}}_{2}&-\hat{\mathbf{z}}_{1}^{\top}\hat{H}^{-1}\hat{\mathbf{z}}_{2} \\ -\hat{\mathbf{z}}_{1}^{\top}\hat{H}^{-1}\hat{\mathbf{z}}_{2}& \hat{\mathbf{z}}_{1}^{\top}\hat{H}^{-1}\hat{\mathbf{z}}_{1} \end{array}\right). $$

Then, the dual problem of (16) can be stated as follows:

$$ \begin{array}{llllll} \max_{\mathbf{z}_{i},\mathbf{u}_{i} } & \ \frac{1}{2}\frac{\|\hat{H}^{-1/2}(\hat{\mathbf{z}}_{2}-(1-\epsilon)\hat{\mathbf{z}}_{1})\|^{2}}{(\|\hat{H}^{-1/2}\hat{\mathbf{z}}_{1}\|\|\hat{H}^{-1/2}\hat{\mathbf{z}}_{2}\|)^{2}-(\hat{\mathbf{z}}_{1}^{\top} \hat{H}^{-1}\hat{\mathbf{z}}_{2})^{2}}\\ \text{s.t.}\, &\, \mathbf{z}_{1}\in \mathbf{B}({\boldsymbol{\mu}}_{2},S_{2},\kappa_{1}),\quad \mathbf{z}_{2}\in \mathbf{B}({\boldsymbol{\mu}}_{3},S_{3},\kappa_{2}), \end{array} $$

(A.38)

where

$$ \mathbf{B}({\boldsymbol{\mu}},S,\kappa)=\{\mathbf{z}:{\mathbf{z}}={\boldsymbol{\mu}}+\kappa S\mathbf{u},\|\mathbf{u}\|\le1\}. $$

(A.39)

Similarly, since the symmetric matrix $\hat {G}=G^{\top } G+\theta _{2}I$ is positive definite, for any 𝜃 ₂ > 0, we can show that the dual of the problem (17) is given by

$$ \begin{array}{llllll} \max_{\mathbf{p}_{i},\mathbf{u}_{i} } & \ \frac{1}{2}\frac{\|\hat{G}^{-1/2}(\hat{\mathbf{p}}_{2}-(1-\epsilon)\hat{\mathbf{p}}_{1})\|^{2}}{(\|\hat{G}^{-1/2}\hat{\mathbf{p}}_{1}\|\|\hat{G}^{-1/2}\hat{\mathbf{p}}_{2}\|)^{2}-(\hat{\mathbf{p}}_{1}^{\top} \hat{G}^{-1}\hat{\mathbf{p}}_{2})^{2}}\\ \text{s.t.}\, &\, \mathbf{p}_{1}\in \mathbf{B}({\boldsymbol{\mu}}_{1},S_{1},\kappa_{3}),\quad \mathbf{p}_{2}\in \mathbf{B}({\boldsymbol{\mu}}_{3},S_{3},\kappa_{4}), \end{array} $$

(A.40)

where $\hat {\mathbf {p}}_{i}=[\mathbf {p}_{i};1]\in \Re ^{n+1}$, for i = 1, 2.