Fuzzy mathematical morphology for biological image segmentation

Abstract

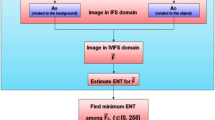
Due to the imaging devices, real-world images such as biological images may have poor contrast and be corrupted by noise, so that regions in the images present soft edges and their segmentation turns out to be quite difficult. Fuzzy mathematical morphology can be successfully applied to segment biological images having such characteristics of vagueness and imprecision. In this work we introduce an approach based on fuzzy mathematical morphology to segment images of human oocytes in order to extract the oocyte region from the entire image. The approach applies fuzzy morphological operators to detect soft edges in the oocyte images, followed by morphological reconstruction operators to isolate the oocyte region. The main concepts from fuzzy mathematical morphology are briefly introduced and the results of applying fuzzy morphological operators are reported in low-contrast images of human oocytes.

Appendix: Binary morphology

Let U be a nonempty set called a universe, and let P(U) be the family of all subsets of U. If we choose $U = \mathbb{R}^{d}$, the d-dimensional Euclidean space, a subset A of U represents a continuous binary image on U. In the particular case $U= \mathbb {Z}^{2}$ the subset A⊂U represents a discrete binary image on U.

In the same way a structuring element is a particular set $B \subset \mathbb{Z}^{2}$, that gets translated over X and whose relations with X are studied at each location. In the following, we denote by B _x the translation of B by x.

Based on these definitions, binary operators are defined as following. Given an image A and a binary structuring element B, with A and B subsets in $\mathbb{Z}^{2}$, the dilation of A by B is defined as:

$$ \delta_B(A)=A \oplus B =\bigcup_{y\in B} A_y=\bigl\{ y \in\mathbb{Z}^2 \mid \check{B}_y \cap A \neq\emptyset\bigr\} $$

(32)

where B _y denotes the translation of B along the vector y, that is B _y ={b+y∣b∈B} and $\check{B}$ denotes the reflection of B along the origin, that is $\check{B}=\{-b \mid b\in B\}$. In other words, the dilation of image A by element B is the set union of all translations y such that A and $\check{B}$ overlap by at least one element.

The erosion of A by B is defined as:

$$ A \ominus B=\bigl\{ y \in\mathbb{Z}^2 \mid B_y \subseteq A \bigr\} $$

(33)

In other words, the erosion of A by B is the set of all points y such that B translated by y is contained in A.

The most important relation between dilation and erosion is the adjunction relation, defined as:

$$ I \oplus B \subseteq A \quad {\Leftrightarrow}\quad I \subseteq A\ominus B $$

(34)

The adjunction relation is considered the most general as well as the most powerful duality relation between dilations and erosions. In general, dilation and erosion are not inverse operators. More specifically, if an image A is eroded by an element B and then dilated by B, the resulting set is not the original set A but a subset of it, in most cases this set is smaller than A. It is called the opening of A by B, denoted by A∘B. Formally, the opening of a binary image A by a binary structuring element B is defined by

$$ A \circ B=(A\ominus B)\oplus B $$

(35)

The geometric interpretation of the opening A∘B is that the opening is the union of all translations of B that are contained in A. Consequently, the binary opening will suppress small peaks and eliminate other small details. In either case, the result of iteratively applied dilations and erosions is the elimination of specific image details smaller than the structuring element used.

Dually, if A is first dilated by B and then eroded by B we get a set which contains the original set A, and in most cases, is larger than A. It is called the closing of A by B, denoted by A•B. Formally, the closing of a binary image A by a binary structuring element B is defined as

$$ A \bullet B=(A \oplus B)\ominus B $$

(36)

If we apply the definition of erosion and dilation in (36) we obtain a geometric interpretation of the closing A•B, that consists of all points $y\in\mathbb{Z}^{2}$ for which any translation of B that contains y has a nonempty intersection with A. As a consequence, the binary closing will fill up small gaps on the contour, eliminate small holes, fuse narrow breaks and long thin gulfs, smooth the contours.

Finally, it is worth to note that the combination of dilation and erosion leads to other operators on binary images, such as connected components and region filling.