Skip to main content
SpringerLink
Log in

Study on wave dispersion characteristics of piezoelectric sandwich nanoplates considering surface effects

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

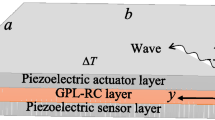
In this study, the wave propagation properties of piezoelectric sandwich nanoplates deposited on an orthotropic viscoelastic foundation are analyzed by considering the surface effects (SEs). The nanoplates are composed of a composite layer reinforced by graphene and two piezoelectric surface layers. Utilizing the modified Halpin-Tsai model, the material parameters of composite layers are obtained. The displacement field is determined by the sinusoidal shear deformation theory (SSDT). The Euler-Lagrange equation is derived by employing Hamilton’s principle and the constitutive equations of piezoelectric layers considering the SEs. Subsequently, the nonlocal strain gradient theory (NSGT) is used to obtain the equations of motion. Next, the effects of scale parameters, graphene distribution, orthotropic viscoelastic foundation, and SEs on the propagation behavior are numerically examined. The results reveal that the wave frequency is a periodic function of the orthotropic angle. Furthermore, the wave frequency increases with the increase in the SEs.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. KARROUBI, R. and IRANI-RAHAGHI, M. Rotating sandwich cylindrical shells with an FGM core and two FGPM layers: free vibration analysis. Applied Mathematics and Mechanics (English Edition), 40(4), 563–578 (2019) https://doi.org/10.1007/s10483-019-2469-8

    Article  MathSciNet  Google Scholar 

  2. AZARIPOUR, S. and BAGHANI, M. Vibration analysis of FG annular sector in moderately thick plates with two piezoelectric layers. Applied Mathematics and Mechanics (English Edition), 40(6), 783–804 (2019) https://doi.org/10.1007/s10483-019-2468-8

    Article  MathSciNet  Google Scholar 

  3. SHABAN, M. and MAZAHERI, H. Bending analysis of five-layer curved functionally graded sandwich panel in magnetic field: closed-form solution. Applied Mathematics and Mechanics (English Edition), 42(2), 251–274 (2021) https://doi.org/10.1007/s10483-021-2675-7

    Article  MathSciNet  Google Scholar 

  4. CAO, D. X. and HU, W. H. Modeling and power performance improvement of a piezoelectric energy harvester for low-frequency vibration environments. Acta Mechanica Sinica, 35(4), 894–911 (2019)

    Article  MathSciNet  Google Scholar 

  5. QIAN, D. Electro-mechanical coupling wave propagating in a locally resonant piezoelectric/elastic phononic crystal nanobeam with surface effects. Applied Mathematics and Mechanics (English Edition), 41(3), 425–438 (2020) https://doi.org/10.1007/s10483-020-2586-5

    Article  MathSciNet  Google Scholar 

  6. FANG, X. Q., ZHU, C. S., LIU, J. X., and LIU, X. L. Surface energy effect on free vibration of nano-sized piezoelectric double-shell structures. Physica B: Condensed Matter, 529, 41–56 (2018)

    Article  Google Scholar 

  7. ZHU, C. S., FANG, X. Q., and YANG, S. P. Nonlinear free vibration of functionally graded viscoelastic piezoelectric doubly curved nanoshells with surface effects. European Physical Journal Plus, 134, 486 (2019)

    Article  Google Scholar 

  8. KACHAPI, S., DARDEL, M., DANIALI, H. M., and FATHI, A. Pull-in instability and nonlinear vibration analysis of electrostatically piezoelectric nanoresonator with surface/interface effects. Thin-Walled Structures, 143, 106210 (2019)

    Article  Google Scholar 

  9. PENG, W., CHEN, L., and HE, T. Nonlocal thermoelastic analysis of a functionally graded material microbeam. Applied Mathematics and Mechanics (English Edition), 42(6), 855–870 (2021) https://doi.org/10.1007/s10483-021-2742-9

    Article  MathSciNet  Google Scholar 

  10. SONG, R., SAHMANI, S., and SAFAEI, B. Isogeometric nonlocal strain gradient quasi-three-dimensional plate model for thermal postbuckling of porous functionally graded microplates with central cutout with different shapes. Applied Mathematics and Mechanics (English Edition), 42(6), 771–786 (2021) https://doi.org/10.1007/s10483-021-2725-7

    Article  MathSciNet  Google Scholar 

  11. MA, L. H., KE, L. L., WANG, Y. Z., and WANG, Y. S. Wave propagation analysis of piezoelectric nanoplates based on the nonlocal theory. International Journal of Structural Stability and Dynamics, 18(4), 1850060 (2018)

    Article  MathSciNet  Google Scholar 

  12. MA, L. H., KE, L. L., WANG, Y. Z., and WANG, Y. S. Wave propagation in magneto-electro-elastic nanobeams via two nonlocal beam models. Physica E: Low-dimensional Systems and Nanostructures, 86, 253–261 (2017)

    Article  Google Scholar 

  13. MA, L. H., KE, L. L., REDDY, J. N., YANG, J., KITIPORNCHAI, S., and WANG, Y. S. Wave propagation characteristics in magneto-electro-elastic nanoshells using nonlocal strain gradient theory. Composite Structures, 199, 10–23 (2018)

    Article  Google Scholar 

  14. FATHI, M. and GHASSEMI, A. The effects of surface stress and nonlocal small scale on the uniaxial and biaxial buckling of the rectangular piezoelectric nanoplate based on the two variable-refined plate theory. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 39, 3203–3216 (2017)

    Article  Google Scholar 

  15. EBRAHIMI, F. and BARATI, M. R. Dynamic modeling of embedded nanoplate systems incorporating flexoelectricity and surface effects. Microsystem Technologies, 25(1), 175–187 (2019)

    Article  Google Scholar 

  16. ZHANG, L. L., LIU, J. X., FANG, X. Q., and NIE, G. Q. Effects of surface piezoelectricity and nonlocal scale on wave propagation in piezoelectric nanoplates. European Journal of Mechanics-A/Solids, 46(4), 22–29 (2014)

    Article  Google Scholar 

  17. GHORBANPOUR-ARANI, A., JAMALI, M., GHORBANPOUR-ARANI, A. H., KOLAHCHI, R., and MOSAYYEBI, M. Electro-magneto wave propagation analysis of viscoelastic sandwich nanoplates considering surface effects. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 231(2), 387–403 (2017)

    Google Scholar 

  18. ZANG, J., FANG, B., ZHANG, Y. W., YANG, T. Z., and LI, D. H. Longitudinal wave propagation in a piezoelectric nanoplate considering surface effects and nonlocal elasticity theory. Physica E: Low-dimensional Systems and Nanostructures, 63, 147–150 (2014)

    Article  Google Scholar 

  19. LIM, C. W., ZHANG, G., and REDDY, J. N. A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. Journal of the Mechanics and Physics of Solids, 78, 298–313 (2015)

    Article  MathSciNet  Google Scholar 

  20. EBRAHIMI, F. and DABBAGH, A. Wave propagation analysis of embedded nanoplates based on a nonlocal strain gradient-based surface piezoelectricity theory. European Physical Journal Plus, 132(11), 449 (2017)

    Article  Google Scholar 

  21. AHAD, A., ROOHOLLAH, T., and LI, L. Wave propagation in viscous-fluid-conveying piezoelectric nanotubes considering surface stress effects and Knudsen number based on nonlocal strain gradient theory. European Physical Journal Plus, 133(7), 252 (2018)

    Article  Google Scholar 

  22. KARIMI, M. Rate of surface energy changes on the wave propagation analysis of METE nanoplates based on couple stress small-scale and nonlocal strain gradient theories. Materials Research Express, 6, 085087 (2019)

    Article  Google Scholar 

  23. GHORBANPOUR-ARANI, A. and JALAEI, M. H. Transient behavior of an orthotropic graphene sheet resting on orthotropic visco-Pasternak foundation. International Journal of Engineering Science, 103, 97–113 (2016)

    Article  MathSciNet  Google Scholar 

  24. GHORBANPOUR-ARANI, A., MOSAYYEBI, M., KOLAHDOUZAN, F., KOLAHCHI, R., and JAMALI, M. Refined zigzag theory for vibration analysis of viscoelastic functionally graded carbon nanotube reinforced composite microplates integrated with piezoelectric layers. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 231(13), 2464–2478 (2017)

    Article  Google Scholar 

  25. GHORBANPOUR-ARANI, A., JAFARI, G. S., and KOLAHCHI, R. Nonlinear vibration analysis of viscoelastic micro nano-composite sandwich plates integrated with sensor and actuator. Microsystem Technologies, 23, 1509–1535 (2017)

    Article  Google Scholar 

  26. KOLAHCHI, R. A comparative study on the bending, vibration and buckling of viscoelastic sandwich nano-plates based on different nonlocal theories using DC, HDQ and DQ methods. Aerospace Science and Technology, 66, 235–248 (2017)

    Article  Google Scholar 

  27. EBRAHIMI, F. and DABBAGH, A. Wave dispersion characteristics of embedded graphene platelets-reinforced composite microplates. European Physical Journal Plus, 133(4), 151 (2018)

    Article  Google Scholar 

  28. PASHMFOROUSH, F. Statistical analysis on free vibration behavior of functionally graded nanocomposite plates reinforced by graphene platelets. Composite Structures, 213, 14–24 (2019)

    Article  Google Scholar 

  29. SOBHY, M. Differential quadrature method for magneto-hygrothermal bending of functionally graded graphene/Al sandwich-curved beams with honeycomb core via a new higher-order theory. Journal of Sandwich Structures and Materials, 23(5), 1662–1700 (2020)

    Article  Google Scholar 

  30. BISHEH, H., WU, N., and RABCZUK, T. Free vibration analysis of smart laminated carbon nanotube-reinforced composite cylindrical shells with various boundary conditions in hygrothermal environments. Thin-Walled Structures, 149, 106500 (2019)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Applied Mechanics and Structure Safety Key Laboratory of Sichuan Province, School of Mechanics and Aerospace Engineering, Southwest Jiaotong University, Chengdu, 610031, China

    Biao Hu, Juan Liu, Yuxing Wang, Bo Zhang & Huoming Shen

  2. School of Mechanical and Electrical Engineering, Southwest Petroleum University, Chengdu, 610500, China

    Jing Wang

Authors
  1. Biao Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Juan Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yuxing Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Bo Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Jing Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Huoming Shen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Juan Liu.

Additional information

Citation: HU, B., LIU, J., WANG, Y. X., ZHANG, B., WANG, J., and SHEN, H. M. Study on wave dispersion characteristics of piezoelectric sandwich nanoplates considering surface effects. Applied Mathematics and Mechanics (English Edition), 43(9), 1339–1354 (2022) https://doi.org/10.1007/s10483-022-2897-9

Project supported by the National Natural Science Foundation of China (Nos. 11502218, 11672252, 11602204, and 12102373) and the Fundamental Research Funds for the Central Universities of China (No. 2682020ZT106)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hu, B., Liu, J., Wang, Y. et al. Study on wave dispersion characteristics of piezoelectric sandwich nanoplates considering surface effects. Appl. Math. Mech.-Engl. Ed. 43, 1339–1354 (2022). https://doi.org/10.1007/s10483-022-2897-9

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-022-2897-9

Key words

Chinese Library Classification

2010 Mathematics Subject Classification

Search

Navigation