Capital exploitation and environmental awareness: How they affect the economy and the environment in a dynamic framework

Abstract

We present a model in which capital and environmental quality co-evolve over time. To improve the environmental quality, the government intervenes by means of a limitation of the capital use and awareness campaigns. In case of severe degradation of the environment, a restriction on capital use is introduced that is proportional to the damage caused by human activity; at the same time, awareness campaigns are used to increase the public concern about sustainability. By means of a discrete-time dynamical system and considering homogeneous agents, we found that multiple equilibria may exist and that awareness campaigns are a useful tool to push an economy toward sustainable levels of production. The limitation in the use of available capital, however, might be useless or even harmful, deteriorating the level of capital disposable for those countries that are trapped in an equilibrium in which the environmental quality is low.

1 Introduction

Climate change is a global concern: it affects ecosystems, biodiversity, water resources, and human settlements. Consequently, it threatens human well-being, socio-economic activities, and economic output. The main driver of climate change is the emission of greenhouse gases (GHGs) from human activity: it amplifies the natural greenhouse effect, modifying the so-called "earth-atmosphere energy balance". The leading contributor to GHG emissions is carbon dioxide ($\hbox {CO}_2$), mainly generated from the combustion of fossil fuels and deforestation. The main challenge is to reduce GHG emissions from human activity, which has to be done by implementing low-carbon strategies, decoupling GHG emissions from economic growth, and reducing domestic emissions (OECD, 2022). To reach this goal, the 2030 Agenda for Sustainable Development identified as key factors the implementation of sustainable production patterns, the achievement of sustainable management and efficient use of natural resources, and the promotion of public awareness for sustainable development and lifestyles in harmony with nature (Goal 12). Many national and international actions have been taken to support sustainable growth: in the last two decades, a total number of 438 policies have been developed worldwide to promote the shift to sustainable consumption and production (United Nations, 2022). However, in 2022 the Sustainable Development Goals Report 2022 (United Nations, 2022) sounded an alarm:

"Using the latest available data and estimates, it reveals that the 2030 Agenda for Sustainable Development is in grave jeopardy. [...] To avoid the worst effects of climate change, as set out in the Paris Agreement, global greenhouse gas emissions will need to peak before 2025 and then decline by 43 percent by 2030, falling to net zero by 2050. Instead, under current voluntary national commitments to climate action, greenhouse gas emissions will rise by nearly 14 percent by 2030."

The severity and magnitude of this scenario have been exacerbated since 2019 by the COVID-19 pandemic and the increasing number of violent conflicts,¹ but the global GHGs emissions trend has preexisting roots. Despite the effort made by the main International Agreements² and the progress achieved in decoupling GHG emissions from GDP growth, emissions continue to grow and the increase of the global temperature persists (see Fig. 1).

Fig. 1

$\hbox {CO}_2$ emissions source: OECD (2022). Air and GHG emissions (indicator). Temperature source: GISS Surface Temperature Analysis (GISTEMP), version 4. NASA Goddard Institute for Space Studies

Environmental policies seem not to be effective and the goals of the 2030 Agenda for Sustainable Development (ASD) appear unattainable. In this view, the contribution of researchers and academics is essential to understand the complex relationship between economic growth, environmental well-being, and the policy framework.

By means of an intertemporal optimization problem, Antoci et al. (2021a) studied the substitution mechanism between a free public environmental good and a costly private good that can be used as a substitute for the environment. Such substitution is realized by economic agents to avoid environmental depletion. They showed that the substitution mechanism may increase the uncertainty on the future environmental trajectories. Similar results are shown in the case in which agents derive utility from leisure, a public environmental good, and the consumption of a produced good (Antoci et al., 2021b), or when individuals react to environmental damages through mitigation (reducing production) or adaptation (increasing expenditures to defend from the loss due to environmental degradation) (Antoci et al., 2019). The above-mentioned works partially explain the unfulfilled targets of the 2030 ASD: on the one hand, they show that consumers’ decisions may generate multiple long run dynamics, on the other they do not take into consideration the potential effect of government policies.

Governments play a crucial role in sustainability. Among the actions of the 2030 ASD, the United Nations explicitly includes the provision of taxation to rationalize inefficient fossil-fuel subsidies that encourage wasteful consumption (Goal 12.c) and the provision of policies to ensure that individuals have the relevant information and awareness for sustainable development and lifestyles in harmony with nature (Goal 12.8). These efforts must be taken into consideration when investigating the co-evolution of the economy and the environment. The early works of Bovenberg and Smulders (1995) and Ewijk and Wijinbergen (1995) showed a positive relation between environmental taxation, quality of the environment, and economic growth, but they do not investigate the transitional dynamics of the models. An extension in the model by Antoci et al. (2021a) considers the case in which negative externalities are taxed, but they assume that the tax is in force regardless of the quality of the environment, while it is reasonable to think that when the economy reaches a high level of sustainability (i.e. the environment is not threatened anymore), environmental taxes would be abandoned. Moreover, none of the considered papers includes in the picture the effect of governments’ policies intended to increase the awareness of individuals regarding sustainable development and sustainable lifestyle. Many of these papers found that multistability may appear.

The main goal of the present work, starting from the existing literature, is to consider the role played by two actions that might be implemented by the governments to improve environmental quality. More specifically we assume that, in case of a severe degradation of the environment, a restriction on resource utilization is introduced that is proportional to the damage caused by human activity; the reduction of resource utilization and thus the contraction of production modeled in this paper can be seen as a measure applied by the government that attempts to replicate in a simplistic form the system of limiting CO2 emissions introduced in European Union countries (Emission Trading System). At the same time, resources are used to increase public awareness about sustainability. Awareness campaigns are active when efficient: when the quality of the environment is already high, such effort would be unnecessarily expensive, therefore they are not used. We found that awareness campaigns are a useful tool to push an economy toward the equilibrium with a high level of environmental sustainability. Conversely, restriction on resource utilization cannot influence the qualitative behavior of the system and might be useless or even harmful, deteriorating the level of capital disposable for those countries that are trapped in a bad equilibrium.

The rest of the paper is organized as follows. Section 2 describes the dynamical system under investigation, Sect. 3 studies the existence and stability of equilibria by means of analytical tools and numerical simulations, Sect. 4 discusses the main findings and Sect. 5 concludes.

2 The model

We introduce the discrete-time dynamical system for the evolution of the economy and the environment. The two-dimensional model describes how the decisions made by the consumers and the government affect the long-run evolution of the system: at each time step individuals allocate their endowment between consumption, savings, and environment preservation depending on their expected utility, while the government interacts with firms and individuals by means of restriction on resource utilization and awareness campaigns depending on the quality of the environment.

2.1 Production

We assume a representative firm exists that employs labor force and physical capital to produce output. Following de la Croix and Michel (2002) we assume that at time $t\in {\mathbb {N}}$ the supply of the physical good $Y_t>0$ is given by the total production function:

$$\begin{aligned} F(K_t,L_t)={\bar{F}}(K_t,L_t)+(1-\delta )K_t \end{aligned}$$

(1)

where $K_t>0$ is the level of capital at the beginning of the period, $L_t>0$ is the labor force, $\delta \in [0,1]$ is the depreciation rate of capital and ${\bar{F}}(\cdot )$ represents the production technology, homogeneous of degree one which implies Constant Returns to Scale (CRS). Note that the total production function F implies that after the production process, the part of capital that is not depreciated is identical to the good produced. Given CRS, the output per worker $y_t=Y_t/L_t$ is

$$\begin{aligned} y_t=f(k_t)=F\left( \frac{K_t}{L_t},1\right) \end{aligned}$$

where $k_t=K_t/L_t$ is the capital per worker and $f(k_t)$ is the intensive form of production function. The firm maximizes profits: it employs labor up to the point in which the change in the level of output for an additional unit of labor equals its wage. The marginal product of labor is

$$\begin{aligned} \frac{\partial }{\partial L_t}F(K_t,L_t)=\frac{\partial }{\partial L_t}\left[ L_t f(k_t)\right] =f(k_t)-k_tf'(k_t). \end{aligned}$$

Therefore the wage is

$$\begin{aligned} w_t=f(k_t)-k_tf'(k_t) \end{aligned}$$

(2)

which implies that the old households receive

$$\begin{aligned} \pi _t=y_t-w_t=f'(k_t) k_t \end{aligned}$$

(3)

and the marginal product of capital $f'(k_t)$ represents the real interest rate:

$$\begin{aligned} r_t=f'(k_t). \end{aligned}$$

(4)

Recalling that $Y_t=L_ty_t=L_tf(k_t)$ and combining equations (1), (2), (3) and (4), it follows

$$\begin{aligned} Y_t=r_t K_t+w_tL_t. \end{aligned}$$

Previous equality states that the total output $Y_t$ is fully exhausted by factor payments.

2.2 Environment

Natural resources and ecosystems at time t are described by the index of the environment $E_t\ge 0$ (in the following we will refer to it as the level or quality of the environment). It is well known that, without human activity, the evolution of the environment would converge to its natural equilibrium (${\bar{E}}$ in the following) determined by the interaction between species. Nevertheless, as highlighted in Srebotnjak et al. (2010), these natural systems can withstand disruption only up to a certain threshold: if the level of the environment is below such threshold, irreversible consequences are likely to occur. This does not necessarily mean extinction, but the vanishment of the environment as known up to that point. We include these considerations in our work and model the evolution of the environment without human activity as

$$\begin{aligned} E_{t+1}= \frac{\left( {\bar{E}}^2 +1\right) E_t^2}{{\bar{E}} (1+E_t^2) } \end{aligned}$$

(5)

where ${\bar{E}}\gg 1$ is the carrying capacity of the natural resource.

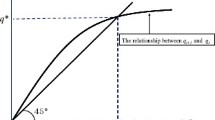
Equation (5) has some interesting properties: as visible in Fig. 2, a threshold level $1/{\bar{E}}$ exists such that, if $E_t$ is below the threshold, the environment will disappear in the long run. Conversely, for $E_t>1/{\bar{E}}$ and without human activity, the environment will converge to its carrying capacity ${\bar{E}}$. Notice that following these considerations, the evolution of the index $E_t$ without human activity is s-shaped. Our choice is related to the fact that the natural environment without human intervention would reach its equilibrium and could not increase without limits: trees and forests could not grow in deserts and oceans, predators and prey would coexist and the overall system would converge to its innate level.

Fig. 2

Evolution of the environment without human activity

However, human activity influences environmental evolution, therefore we have to specify how equation (5) changes depending on the decisions made by individuals. More precisely, at any time t, the level of the environment is negatively affected by the production (measured by $Y_t$) and positively affected by the savings allocated by individuals to preserve the environmental quality (whose level is denoted by $s_{e,t}\ge 0$):

$$\begin{aligned} \begin{array}{l} E_{t+1}=\frac{\left( {\bar{E}}^2 +1\right) E_t^2}{{\bar{E}} (1+E_t^2) }+e_t,\\ e_t=bs_{e,t}-aY_t. \end{array} \end{aligned}$$

(6)

Parameter $a\in (0,1)$ represents the severity of the impact of production: for $a\rightarrow 0$ the production process does not affect the quality of the environment while for $a\rightarrow 1$ each unit of output destroys a unit of environment. Conversely, the effectiveness of measures intended to preserve environmental quality is represented by $b\in (0,1)$. While $s_{e,t}$ is specifically intended to increase the level of the environment, the damage caused by production is a side effect and consequently, it should have a lower intensity per unit of capital, say $0<a<b$. We make additional considerations setting $0<a<(1-\alpha )b$ where $\alpha \in (0,1)$ is the output elasticity of capital³: a high output elasticity of capital leads to energy conservation and consequently the impact on the environment is limited when compared to the case of low values of $\alpha$ (Lin & Liu, 2017). The two addends in $e_t$ have the same order of magnitude since $s_{e,t}$ is part of the wages allocated to environmental preservation. Notice that, given the previous assumption, we consider the case in which the society intends at least to preserve environmental quality ($e_t$ non-negative) while a further study could investigate the case in which $e_t$ might be negative.

2.3 Consumers

Consumers are represented by a two-period overlapping generations model. As in Antoci et al. (2021a) and Naimzada and Sodini (2010), the population is constant and normalized to one, i.e. $L_t=L=1$, $\forall t$. Individuals are born without endowment, they work and earn wage income when young while they consume in each period. Labor is supplied inelastically and individuals have preferences regarding the present consumption, the expected consumption, and the increase in the level of the environmental good that can be generated thanks to human activity. We assume that the lifetime utility function is

$$\begin{aligned} V(c^Y_t,c^O_{t+1}, e_t)=u(c^Y_t)+\beta [u({\mathbb {E}}[c^O_{t+1}])+u(e_{t})] \end{aligned}$$

(7)

where $\beta \in (0,1)$ is the subjective discount rate, $e_{t}$ is the increase in the level of the environment due to human activity, while $c^Y_t$ and $c^O_{t+1}$ are the consumptions when young ($c^Y_t$) and old ($c^O_{t+1}$) of an individual born in t. The utility function is logarithmic: $u(x)=\log (x)$.

Agents maximize (7) subject to the budget constraints

$$\begin{aligned} \begin{array}{c} c^Y_t=w_t-s_{c,t}-s_{e,t}\\ {\mathbb {E}}[c^O_{t+1}]=\left( 1+{\mathbb {E}}[r_{t+1}]\right) s_{c,t} \end{array} \end{aligned}$$

(8)

where $s_{c,t}$ are savings allocated to future consumption and $s_{e,t}$ is the portion of savings that each agent allocates to increase the environmental quality. Note that the use of the logarithmic utility function eliminates the dependence of the decision on the expected interest rate ${\mathbb {E}}[r_{t+1}]$, (as it will be clear in the following) therefore no specification of ${\mathbb {E}}[r_{t+1}]$ is needed.

2.4 Government

In order to restore the quality of the environment, the government might opt for measures intended to increase the sensibility of individuals regarding sustainability, or it might introduce an restriction on resource utilization. The first measure is implemented by applying policies that increase, for the individuals, the utility of the environment. Such a measure might be ineffective and unnecessarily expensive when the level of the environment is excessively low as well as in the case of $E_t\ge {\bar{E}}$. Therefore, the government employs an awareness campaign to raise the utility perceived by individuals, depending on the level $E_t$: for $E_t=0$ the campaign would be ineffective and no campaigns would be active. As $E_t$ increases, the effort of the government to raise the concern about sustainability increases. The maximum effort is set when $E_t={\bar{E}}/2$: when the quality of the environment is in the middle between null and full capacity, an awareness campaign might be crucial, therefore the government undertakes a campaign intended to double the utility generated by the environment. For higher values of $E_t$, the effort of the government decreases since it would be unnecessarily expensive and awareness campaigns are left for $E_t\ge {\bar{E}}$. Such policy is reflected in the individuals’ lifetime utility function which becomes

$$\begin{aligned} V(c^Y_t,c^O_{t+1}, e_t)=u(c^Y_t)+\beta [u({\mathbb {E}}[c^O_{t+1}])+\gamma _tu(e_{t})] \end{aligned}$$

(9)

where we assume

$$\begin{aligned} \gamma _t= {\left\{ \begin{array}{ll} \begin{array}{ll} \frac{4}{{\bar{E}}}E_t(1-\frac{E_t}{{\bar{E}}})+1 &{} E_t<{\bar{E}}\\ 1 &{} E_t\ge {\bar{E}} \end{array} \end{array}\right. }. \end{aligned}$$

(10)

Restriction on resource utilization is a severe measure with critical consequences for the overall economy. For this reason, it should be adopted with caution. We assume that the effect of restriction on resource utilization can be represented by a reduction in the input available for production. The production technology is represented by the Cobb-Douglas function:

$$\begin{aligned} {\bar{F}}(K_t,1)=K_t^\alpha \end{aligned}$$

therefore, according to equation (1) it has

$$\begin{aligned} Y_t= K_t^\alpha +(1-\delta ) K_t. \end{aligned}$$

The two equations above refer to the case where there is no government intervention. The government reduces resource utilization by applying a restriction $g_t$ on the available capital it has:

$$\begin{aligned} Y_t=(g_tK_t)^\alpha +(1-\delta ) g_tK_t \end{aligned}$$

(11)

from which it follows that after the intervention of the government, it has

$$\begin{aligned} r_t=\alpha g_t^\alpha K_t^{\alpha -1}+(1-\delta )g_t \end{aligned}$$

(12)

and

$$\begin{aligned} w_t=(1-\alpha )g_t^\alpha K_t^\alpha , \end{aligned}$$

(13)

where we assume

$$\begin{aligned} g_t= {\left\{ \begin{array}{ll} \begin{array}{ll} 1-d+\frac{2d}{{\bar{E}}}E_t &{} E_t<\bar{E}/2\\ 1 &{} E_t\ge \bar{E}/2 \end{array}. \end{array}\right. } \end{aligned}$$

(14)

Parameter $d\in (0,1)$ determines the severity of the restriction. Notice that we apply a restriction on capital utilization before production begins. The rationale concerns harmful emissions generated with the available capital.⁴

When $E_t=0$ the available capital for production is $g_t(0)=1-d$. The restriction decreases as $E_t$ increases and it is not applied for $E_t\ge {\bar{E}} /2$.

Fig. 3

Values of $\gamma _t$ (panel a) and $g_t$ (panel b) depending on $E_t$. ${\bar{E}}=4$

Figure 3 shows the intensity of the two government measures depending on the level of the environment. As visible in panel (a), awareness campaigns increase the utility that comes from the future quality of the environment (by means of $\gamma _t$) and they are active only in case $E_t<{\bar{E}}$ with maximum effort when $E_t={\bar{E}}/2$. The abrupt change in $\gamma _t$ for $E_t=\bar{E}$ represents the moment in which the government abandons awareness campaigns: when the index $E_t$ is above the value ${\bar{E}}$, such campaigns would be unnecessarily expensive and are therefore not used. Panel (b) shows the contraction in production (by means of $g_t$), for different values of d: the higher parameter d the lower the capital available for production; lower values of d represent a mild restriction. For $E_t\ge {\bar{E}}/2$ no restriction is applied since the government does not levy restrictions related to the environmental quality.

2.5 Consumption choices

Given the budget constraints in (8) and substituting equation (6) in (9), the lifetime utility function becomes

$$\begin{aligned} V(s_{c,t}, s_{e,t})=\log (w_t-s_{c,t}-s_{e,t})+\beta \left[ \log (1+r_t)+\log (s_{c,t})+\gamma _t\log (bs_{e,t}-aY_t)\right] . \end{aligned}$$

The optimization problem has a unique solution given by

$$\begin{aligned} \begin{array}{l} s_{e,t}=\frac{\beta \gamma _tbw_t+(1+\beta )aY_t}{(1+\beta +\gamma _t\beta )b},\quad s_{c,t}=\frac{bw_t-aY_t}{(1+\beta +\gamma _t\beta )b}\beta . \end{array} \end{aligned}$$

(15)

The restriction on resource utilization reduces the two solutions $s_{e,t}$, $s_{c,t}$: a lower output implies lower wages for the individuals and, consequently, a lower amount to be allocated between savings and environmental protection. Conversely, a higher $\gamma _t$ increases the amount allocated to the preservation of the environment while decreasing $s_{c,t}$: this policy does not affect the total amount held by individuals, it modifies only their priorities. Note how the first type of policy can be seen as an income effect since it alters disposable income, while the second type of intervention can be seen as a substitution effect since it does not alter disposable income but changes the way it is allocated by consumers.

2.6 Evolution of the economy and the environment

We are now able to describe the evolution of the economy and that of the environment depending on the consumption choices of individuals. At each time step, young individuals consume $c^Y_t=w_t-s_{e,t}-s_{c,t}$ and allocate $s_{e,t}$ to environment preservation while old individuals only consume for the amount

$$\begin{aligned} c^O_t=(1+r_t)s_{c,t-1}. \end{aligned}$$

Given that the population is normalized to one, the capital available at time $t+1$ is then equal to the saving rate $s_{c,t}$.

Considering equations (12), (13) and (15), the evolution of capital is

$$\begin{aligned} K_{t+1}=\frac{[b(1-\alpha )-a]g_t^\alpha K_t^\alpha -a(1-\delta )g_tK_t}{(1+\beta +\gamma _t \beta )b}\beta \end{aligned}$$

where

$$\begin{aligned} g_t= {\left\{ \begin{array}{ll} \begin{array}{ll} 1-d+\frac{2d}{{\bar{E}}}E_t, &{} E_t<\bar{E}/2\\ 1, &{} E_t\ge \bar{E}/2 \end{array} \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} \gamma _t= {\left\{ \begin{array}{ll} \begin{array}{ll} \frac{4}{{\bar{E}}}E_t(1-\frac{E_t}{{\bar{E}}})+1, &{} E_t<{\bar{E}}\\ 1, &{} E_t\ge {\bar{E}} \end{array}. \end{array}\right. } \end{aligned}$$

Notice that, in the case where the return of the investment of physical capital made by the old generation is sufficiently higher than the wage of workers (i.e. $\pi _t>(b-a)w_t/a$), the economy would experience negative levels of capital. This may be considered the case of debt and will not be analyzed in this work.⁵

Without human activity, the environment evolves accordingly to (5). Its dynamic is then modified considering the negative effects of production and the positive effects due to the resources allocated to preserve and increase the environmental quality. Substituting equations (11) and (15) in (6), it follows

$$\begin{aligned} E_{t+1}=\frac{\left( {\bar{E}}^2 +1\right) E_t^2}{{\bar{E}} (1+E_t^2) }+\frac{\gamma _t \beta \left\{ [b(1-\alpha )-a]g_t^\alpha K_t^\alpha -a(1-\delta )g_tK_t\right\} }{1+\beta +\gamma _t \beta }. \end{aligned}$$

The final dynamical model for the evolution of the economy and of the environment is

$$\begin{aligned} T(K_t,E_t)= {\left\{ \begin{array}{ll} \begin{array}{lr} T_1(K_t,E_t) &{} E_t< \bar{E}/2\\ T_2(K_t,E_t)\quad &{}\bar{E}/2\le E_t< \bar{E}\\ T_3(K_t,E_t) &{} E_t\ge \bar{E} \end{array} \end{array}\right. } \end{aligned}$$

(16)

where

$$\begin{aligned} T_1 = {\left\{ \begin{array}{ll} \begin{array}{l} K_{t+1}=\frac{[b(1-\alpha )-a]\left( 1-d+\frac{2d}{{\bar{E}}}E_t\right) ^\alpha K_t^\alpha -a(1-\delta )\left( 1-d+\frac{2d}{{\bar{E}}}E_t\right) K_t}{\left\{ 1+\beta +\left[ \frac{4}{{\bar{E}}}E_t(1-\frac{E_t}{{\bar{E}}})+1\right] \beta \right\} \beta ^{-1}b}\\ E_{t+1}=\frac{\left( {\bar{E}}^2 +1\right) E_t^2}{{\bar{E}} (1+E_t^2) }+\frac{ [b(1-\alpha )-a]\left( 1-d+\frac{2d}{{\bar{E}}}E_t\right) ^\alpha K_t^\alpha -a(1-\delta )\left( 1-d+\frac{2d}{{\bar{E}}}E_t\right) K_t }{\left\{ \left[ \frac{4}{{\bar{E}}}E_t(1-\frac{E_t}{{\bar{E}}})+1\right] \beta \right\} ^{-1}\left\{ 1+\beta +\left[ \frac{4}{{\bar{E}}}E_t(1-\frac{E_t}{{\bar{E}}})+1\right] \beta \right\} }\\ \end{array}, \end{array}\right. }\\ T_2 = {\left\{ \begin{array}{ll} \begin{array}{l} K_{t+1}=\frac{[b(1-\alpha )-a] K_t^\alpha -a(1-\delta )K_t}{\left\{ 1+\beta +\left[ \frac{4}{{\bar{E}}}E_t(1-\frac{E_t}{{\bar{E}}})+1\right] \beta \right\} b}\beta \\ E_{t+1}=\frac{\left( {\bar{E}}^2 +1\right) E_t^2}{{\bar{E}} (1+E_t^2) }+\frac{ \left[ \frac{4}{{\bar{E}}}E_t(1-\frac{E_t}{{\bar{E}}})+1\right] \beta \left\{ [b(1-\alpha )-a] K_t^\alpha -a(1-\delta )K_t\right\} }{1+\beta +\left[ \frac{4}{{\bar{E}}}E_t(1-\frac{E_t}{{\bar{E}}})+1\right] \beta }\\ \end{array} \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} T_3 = {\left\{ \begin{array}{ll} \begin{array}{l} K_{t+1}=\frac{[b(1-\alpha )-a]K_t^\alpha -a(1-\delta )K_t}{(1+\beta + \beta )b}\beta \\ E_{t+1}=\frac{\left( {\bar{E}}^2 +1\right) E_t^2}{{\bar{E}} (1+E_t^2) }+\frac{\beta \left\{ [b(1-\alpha )-a] K_t^\alpha -a(1-\delta )K_t\right\} }{1+2\beta }\\ \end{array}. \end{array}\right. } \end{aligned}$$

The evolution of the two-dimensional model will be discussed in the following sections.

3 Existence and stability of the equilibria

In this section, we discuss the existence and the local stability of equilibria for the system (16) making use of analytical tools and numerical simulations. Fixed points are desirable since they represent stationary solutions over time.

Proposition 1

Map $T(K_t,E_t)$ given by (16) admits at least one and at most three fixed points.

More precisely,

• the fixed point $P^\circ =(K^\circ , E^\circ )$ always exists, with $E^\circ >{\bar{E}}$,

• the fixed points $P^*_1=(K^*_1, E^*_1)$ and $P^*_2=(K^*_2, E^*_2)$ may exist, with $E^*_1<E^*_2<1/{\bar{E}}$,

being

$$\begin{aligned} K^*_1=\left\{ \frac{\beta [b(1-\alpha )-a]\left[ \frac{(1-d){\bar{E}}+2d E^*_1}{{\bar{E}}}\right] ^\alpha }{\left( 1+\beta +\frac{4E^*_1{\bar{E}}-4(E^*_1)^2+{\bar{E}}^2}{{\bar{E}}^2}\beta \right) b+a(1-\delta )\left[ \frac{(1-d){\bar{E}}+2d E^*_1}{{\bar{E}}}\right] \beta }\right\} ^\frac{1}{1-\alpha },\\ K^*_2=\left\{ \frac{\beta [b(1-\alpha )-a]\left[ \frac{(1-d){\bar{E}}+2d E^*_2}{{\bar{E}}}\right] ^\alpha }{\left( 1+\beta +\frac{4E^*_2{\bar{E}}-4(E^*_2)^2+{\bar{E}}^2}{{\bar{E}}^2}\beta \right) b+a(1-\delta )\left[ \frac{(1-d){\bar{E}}+2d E^*_2}{{\bar{E}}}\right] \beta }\right\} ^\frac{1}{1-\alpha } \end{aligned}$$

and

$$\begin{aligned} K^\circ =\left\{ \frac{\beta [b(1-\alpha )-a]}{(1+2\beta )b+a(1-\delta )\beta }\right\} ^\frac{1}{1-\alpha }. \end{aligned}$$

Proof is in Appendix A.1. The number of stable fixed points varies, hence, from one to three, depending on parameter values. In this view, the role of b and $\alpha$ will be discussed in the following. While it was possible to prove analytically that it has $E^\circ>E^*_2>E^*_1$ (see Appendix A), further considerations are needed to evaluate the levels of capital in the equilibria. In case $E<1/{\bar{E}}$, the level of capital in a generic fixed point can be written as

$$\begin{aligned} K^*=\left\{ \frac{\beta [b(1-\alpha )-a]g^\alpha }{(1+\beta +\gamma \beta )b+a(1-\delta )g\beta }\right\} ^\frac{1}{1-\alpha }. \end{aligned}$$

(17)

Fig. 4

Value of $K^*$ computed moving E and d for different values of $\alpha$. Parameter values: $\beta =\delta =0.7$, $b=0.5$, $a=0.8b(1-\alpha )$, ${\bar{E}}=6$

As shown in Fig. 4, for $E<1/{\bar{E}}$, the level of capital in equilibrium decreases as d increases or $\alpha$ decreases. This result will be discussed in the next section, nevertheless, it is a rather intuitive consideration. Less obvius is the effect of the parameter d when $K^*_1$ and $K^*_2$ are compared: when d and $\alpha$ are sufficiently high it has $K^*_2>K^*_1$, otherwise $K^*_2<K^*_1$ (see Fig. 5). Moreover, numerous simulations showed that it always has $K^\circ >K^*_{j}$, $j\in \{1,2\}$ and it is easy to prove this result analytically for $\delta =1$. In line with these considerations and based primarily on the levels of environmental quality in equilibrium, we will use good equilibrium below to identify the fixed point $P^\circ$, while the remaining fixed points will be identified as bad equilibria.

Fig. 5

Comparison of $K^*_1$ and $K^*_2$ moving E and d for different values of $\alpha$. Purple region: $K^*_2<K^*_1$; yellow region: $K^*_2>K^*_1$. Parameter values: $\beta =\delta =0.7$, $b=0.5$, $a=0.8b(1-\alpha )$, ${\bar{E}}=6$

Notice that for $\delta =1$ the evolution of capital over time follows

$$\begin{aligned} K_{t+1}=\frac{[b(1-\alpha )-a]g_t^\alpha K_t^\alpha \beta }{(1+\beta +\gamma _t \beta )b} \end{aligned}$$

and all trajectories are feasible. Therefore the above-mentioned case (see Sect. 2.6) in which the economy could reach a negative level of capital cannot appear.

Before proceeding to the analysis of the characteristics of fixed points, let us turn to the study of their stability so that we can identify those equilibria that are significant for the whole system (i.e., stable).

The stability of the fixed point is determined by computing the Jacobian matrix J of the system and evaluating it in the fixed points. Considering that in the fixed points it has $K_t=K_{t+1}=K$, $E_t=E_{t+1}=E$, $g_t=g_{t+1}=g$ and $\gamma _t=\gamma _{t+1}=\gamma$, $\forall t$ with

$$\begin{aligned} g= {\left\{ \begin{array}{ll} \begin{array}{ll} 1-d+\frac{2d}{{\bar{E}}}E &{} E<\bar{E}/2\\ 1 &{} E\ge \bar{E}/2 \end{array}, \end{array}\right. } \quad \gamma = {\left\{ \begin{array}{ll} \begin{array}{ll} \frac{4}{{\bar{E}}}E(1-\frac{E}{{\bar{E}}})+1 &{} E<{\bar{E}}\\ 1 &{} E\ge {\bar{E}} \end{array} \end{array}\right. }. \end{aligned}$$

The Jacobian matrix computed in a generic fixed point is

$$\begin{aligned} J=\left( \begin{array}{cc} \Psi _{KK} &{} \Psi _{KE} \\ \Psi _{EK}&{} \Psi _{EE} \\ \end{array} \right) \end{aligned}$$

where

$$\begin{aligned} \begin{array}{rlrlrlrl} \Psi _{KK}=&\frac{\partial K_{t+1}}{\partial K_t},&\quad \Psi _{KE}=&\frac{\partial K_{t+1}}{\partial E_t},&\quad \Psi _{EK} =&\frac{\partial E_{t+1}}{\partial K_t},&\quad \Psi _{EE} =&\frac{\partial E_{t+1}}{\partial E_t}. \end{array} \end{aligned}$$

In the case where $E>{\bar{E}}$ it has

$$\begin{aligned} \begin{array}{rl} \Psi _{KK}=&{} \alpha -\frac{(1-\alpha )(1-\delta )a\beta }{(1+2\beta )b},\\ \Psi _{KE}=&{} 0,\\ \Psi _{EK} = &{} \alpha b-\frac{(1-\alpha )(1-\delta )a\beta }{(1+2\beta )},\\ \Psi _{EE} =&{}\frac{{\bar{E}}^2+1}{{\bar{E}}}\frac{2E}{(1+E^2)^2}, \end{array} \end{aligned}$$

and the characteristic polynomial is

$$\begin{aligned} \lambda ^2+\left[ \alpha -\frac{(1-\alpha )(1-\delta )a\beta }{(1+2\beta )b}+\frac{2({\bar{E}}^2+1)E}{{\bar{E}}(1+E^2)^2}\right] \lambda + \frac{2({\bar{E}}^2+1)E}{{\bar{E}}(1+E^2)^2}\left[ \alpha -\frac{(1-\alpha )(1-\delta )a\beta }{(1+2\beta )b}\right] =0\nonumber \\ \end{aligned}$$

(18)

whose eigenvalues are

$$\begin{aligned} \begin{array}{c} \lambda _1=\frac{(1-\alpha )(1-\delta )a\beta }{(1+2\beta )b}-\alpha ,\\ \lambda _2=-\frac{2({\bar{E}}^2+1)E}{{\bar{E}}(1+E^2)^2}. \end{array} \end{aligned}$$

It is easy to verify that $-1<\lambda _1<1$ and $-1<\lambda _2<0$ therefore for the fixed point $P^\circ =(K^\circ ,E^\circ )$ it always has $\mid \lambda _j\mid <1,\quad j\in \{1,2\}$. These considerations prove the following proposition:

Proposition 2

The fixed point $P^\circ$ defined in Proposition 1 is always locally asymptotically stable.

In the case where $E<1/{\bar{E}}$ it has

$$\begin{aligned} \begin{array}{rl} \Psi _{KK}=&{} \alpha -\Omega g,\\ \Psi _{KE}=&{} K\left( \frac{\Psi _{KK}}{g}g^\prime -\frac{\beta \gamma ^\prime }{1+\beta +\gamma \beta }\right) ,\\ \Psi _{EK} = &{} \gamma b \Psi _{KK},\\ \Psi _{EE} =&{}\frac{{\bar{E}}^2+1}{{\bar{E}}}\frac{2E}{(1+E^2)^2}+\gamma b \Psi _{KE}, \end{array} \end{aligned}$$

(19)

and

$$\begin{aligned} \Omega =\frac{(1-\alpha )(1-\delta )a\beta }{(1+\beta +\gamma \beta )b}. \end{aligned}$$

Due to the complexity of the equations, we investigate the stability of the fixed points using numerical techniques. The complete set of simulations and a detailed description of the algorithm used is given in Appendix B.

The fixed point $P^{*}_{1}$ is always stable while the fixed point $P^{*}_2$ changes its stability depending on parameter values as follows:

• when $\alpha$ assumes high values the fixed point is stable;

• when $\alpha$ assumes intermediate values the fixed point is stable if b is sufficiently low and a is sufficiently high;

• when $\alpha$ assumes low values the fixed point might be stable or unstable.

The results presented so far are summarized in Remark 1, while the insights arising from them will be addressed in the next section.

Remark 1

Map T always has a stable fixed point given by $P^\circ =(K^\circ ,E^\circ )$.

Moreover, two additional equilibria may exist:

• the fixed point $P^*_1=(K^*_1,E^*_1)$, when it exists, is stable;

• the fixed point $P^*_2=(K^*_2,E^*_2)$, when it exists, is stable if $\alpha$ assumes high values or $\alpha$ assumes intermediate values and b is sufficiently low while a is sufficiently high. The stability of $P^*_2$, when $\alpha$ is low, depends in a more complex way on the combination of the other parameter values.

By summarizing, the levels of K and E in equilibrium are such that:

• $E^\circ>E^*_2>E^*_1$;

• for $E<1/{\bar{E}}$, the level of capital in equilibrium decreases as d increases or $\alpha$ decreases;

• when d and $\alpha$ are sufficiently high, it has $K^*_2>K^*_1$, otherwise $K^*_2<K^*_1$;

• it always results $K^\circ >K^*_j$, $j\in \{1,2\}$.

Note that when several stable equilibria coexist (as in this case) depending on the initial starting condition of the system, one or another equilibrium can be reached indiscriminately depending on the values of the parameters. Therefore, it is important to analyze the basins of attraction of the equilibria to check whether it is possible to direct the path of the whole system toward achieving the desirable equilibrium. These analyses will be performed in the following section.

3.1 Numerical evidences

We now investigate by means of numerical simulations the global dynamics of the system for different choices of the parameters of interest and by considering different initial conditions.

As it has been discussed, the system may admit unfeasible trajectories, since, depending on parameter values, the set ${\mathbb {R}}^2_+$ is not invariant. In fact, the first consideration is that, for instance, an initial condition $(K_0,E_0)$ with very large values for both capital and environmental quality may produce, after one step, a negative $K_1$ value. The following remark holds.

Remark 2

Let $\delta =1$ then the system T given by (16) is feasible for all initial conditions $(K_0,E_0)\in {\mathbb {R}}^2_+$.

For the above-mentioned considerations and following de la Croix and Michel (2002)⁶ we set $\delta =1$.

By taking into account Proposition 1, the model may admit up to three fixed points: one good equilibrium and up to two bad equilibria. The first question to be investigated is then to understand if more than one stable equilibria may coexist and, hence, what happens to their basins of attraction and related structure. By taking into account Remark 1, we observe that the good equilibrium is always locally asymptotically stable and the same occurs for one of the bad equilibrium. Furthermore, since local stability cannot be determined analytically for all fixed points, one may be interested in understanding if more complex dynamics may arise. Such open questions will be attached using numerical simulations. To this aim, we will fix some parameters and focus on the role played by the main parameters of interest on local and global dynamics:

• The strength of the negative effects of production a on the capital and the environment;

• The strength of the positive effects of awareness b on the capital and the environment;

• The role played by the severity of the restriction d.

Regarding other parameters, we will consider opportune values to better show the main results. Then assume $\beta =0.8$, $\alpha =0.4$ and $\bar{E}=2$.

Finally we consider $a=m(1-\alpha )b$ where $m\in (0,1)$. Thus as long as m increases from low to high values, the damage associated with production increases for any fixed measure to preserve environmental quality (i.e. by setting b and d).

We first consider the question of initial conditions. Several numerical experiments show that any initial conditions $(K_0,E_0)$ with $E_0>1/\bar{E}$ produce trajectories converging to the good equilibrium $P^\circ$ for any choice of parameter combinations. As a consequence, the main question is to understand what occurs to systems that at the initial time are characterized by a low environmental quality, i.e., $E_0<1/\bar{E}$.

In Fig. 6 we plot the two variables versus time. We fix $K_0=5$ and we consider different initial conditions for $E_0$, i.e. the quality of the environment at the initial time. In particular, we distinguish between economies starting from very low or low environmental quality levels (i.e. $E_0=0.2$ or $E_0=0.4$). In both cases, at the initial time, the environmental quality is low in the sense that $E_0<1/\bar{E}$ since, as we previously underlined, economies starting from a high environmental quality level will converge to the good equilibrium.

Fig. 6

Evolution of the environment and capital setting $\alpha =0.4$, $b=0.5$, $m=0.3$ and $d=0.4$ for very-low initial environmental quality (in red) and low initial environmental quality (in blue)

By observing Fig. 6, we notice that multiple equilibria may coexist. More precisely, if the initial environmental quality is less than $1/\bar{E}$ but not too low, then in the long term the environmental quality will improve thus reaching an equilibrium value greater than $\bar{E}$ (blue trajectories). On the other hand, a lower level of $E_0$ can produce the situation represented by the red sequences, i.e. the environment will get worse reaching an equilibrium value less than $1/\bar{E}$. We can refer to the latter case as environmental trap to represent the set of initial conditions producing trajectories converging to a bad equilibrium.

When coexisting equilibria emerge, the investigation of the basins of attraction becomes prominent. In addition, since the main goal of the present work is to discuss the role of the awareness policy (whose strength is measured by b) and that of the restriction on resource utilization (whose degree is measured by d), the study of the modification of those basins when moving the two parameters needs to be investigated.

To this aim, we first present the following Fig. 7 in which we fix d and increase b. It can be observed that the size of the basin of the bad fixed point (i.e. with an environment equilibrium level less than $1/\bar{E}$) decreases as long as b increases, providing that public investment in increasing the environmental awareness plays an effective role in reducing the possibility of the environmental trap emerging.

Fig. 7

Basins of attraction of bad (in light blue) and good (in yellow) equlibria by moving b. a $b=0.1$, b $b=0.4$, c $b=0.7$, d $b=0.9$

Regarding the role of restriction on resource utilization measured by parameter d, several numerical experiments show that it does not affect the probability of falling in the environmental trap in the sense that the shape of the basins does not change with d. Hence such a measure seems to be ineffective in moving from bad to good equilibrium. However, what could be of interest is the comparison between the quantitative results. In Fig. 8 we fix $b=0.5$ and let d move.

Fig. 8

Environmental quality and capital level as varying d for two different conditions: very-low initial environmental quality (in red) and low initial environmental quality (in blue). (Color figure online)

As it can be observed, outside the environmental trap, i.e. if the environmental initial quality is not too low, the economy will reach a good equilibrium whose level is not affected by the strength of the restriction on resource utilization. Anyway, if the environmental quality starts from very low levels, then the restriction on resource utilization is not an effective instrument.

Finally, the question of the existence of fluctuations or attractors which are different from the fixed point can be clarified. In fact, all numerical experiments showed that no cycles or complex attractors are present thus confirming that fluctuations in the long term are ruled out.

4 Discussion

In a framework in which production damages the environment (a sufficiently high) and individuals may opt to allocate part of their wealth to environmental protection, we showed that a restriction on resource utilization decreases the amount allocated to production, as well as the amount available for environment preservation, while awareness campaigns increase available resources for the environment and decrease consumers savings allocated to capital growth (see Sect. 2.5).

Our model allows up to three stable equilibria to co-exist in the system: two are called "bad equilibria" ($P^*_1$ and $P^*_2$) because they are characterized by low environmental quality, while the third equilibrium is called "good equilibrium" ($P^\circ$) because it is marked by high levels of environmental quality and capital. The good equilibrium $P^\circ$ and the bed equilibrium $P^*_1$ are always locally stable.

While the above-mentioned finding remains true regardless of any other criteria, the long-run evolution of the overall system depends on the characteristics of the economy under investigation: for developed economies, typically characterized by the highest values of the output elasticity of capital (parameterized by $\alpha$ in this work), a third stable equilibrium, i.e. $P^*_2$, is admitted while for less developed economies such equilibrium may be unstable.

While parameter $\alpha$, and thus the characteristics of the economy, influences the stability of $P^*_2$ and hence the number of stable equilibria, the intervention of the government by means of restriction on resource utilization (parameterized by d) characterizes the levels of capital present in the two bad equilibria: a high restriction corresponds to the case where $K^*_2>K^*_1$. These results draw attention to the global dynamics of the model and how government decisions can influence long-term trends.

Consider, for example, a developing country; we have seen that in such a case the system can have two stable fixed points: the good equilibrium and the bad equilibrium $P^*_1$. In the case where the economy is converging to the bad equilibrium, excessive capital restriction would worsen long-run conditions, leading to a lower level of available capital compared to the level that there would be with a less restrictive policy.

Therefore, it is necessary to ask whether a restriction on resource utilization can change the trajectory taken by a country, shifting it from the path leading to the bad equilibrium and allowing it to reach the positive equilibrium. Similarly, for developed economies in which three stable equilibria coexist, the question must be asked whether it is possible to determine and potentially influence the long-term trend of the system or whether, despite the choices made by consumers and government, the country cannot be steered toward the good equilibrium. These problems have been addressed in Sect. 3.1. We have shown that, as in previous literature, multi-stability may appear, but a restriction on resource utilization and awareness campaigns might be effective tools for a more sustainable economy: when a country experiences a deteriorated environmental quality, the economy might be enclosed in an environmental trap, converging to a bad equilibrium. Nevertheless, the basin of attraction of the above-mentioned trap can be reduced by government intervention: specifically, the interventions that increase the effect of environmental awareness reduce the basin of attraction of the bad equilibrium and may push the country outside of the trap, guaranteeing the convergence to the good equilibrium.

In contrast, restriction on resource utilization is not an effective protection: the basin of attraction of the environmental trap is not affected by resource utilization levels and excessive restrictions can harm the economy leading to lower levels of capital disposable in the bad equilibrium. On the other hand, if the economy is on the path toward good equilibrium, the severity of restriction on resource utilization does not affect the level of capital and the quality of the environment, proving to be unnecessary.

5 Conclusion

We built a model in which capital and environmental quality co-evolve over time. Production has a negative impact on the environment but, on the other hand, the income generated by production might be allocated to preserve environmental quality. The government intervenes using restrictions on resource utilization (when the quality of the environment is excessively low) and awareness campaigns. We found that, as seen in related work, multiple equilibria may coexist.

In this case, awareness campaigns represent a useful tool to push an economy toward an equilibrium characterized by high environmental quality and a high level of capital. Conversely, restriction on resource utilization cannot influence the qualitative behavior of the system (i.e., the long-run evolution of the economy) and might be useless (for those countries that are converging to the good equilibrium) or even harmful, deteriorating the level of capital disposable for those countries that are trapped in a bad equilibrium. Future developments should consider more sophisticated restrictions on resource utilization and taxation tools, in order to test whether such changes in government intervention methods can be effective tools for achieving sustainable levels of production.

Appendices

Appendix A: Proof of Propositions

1.1 A.1 Proof of Proposition 1

Equilibrium points of map (16) are obtained by setting $K_{t+1}=K_t=K$, $E_{t+1}=E_{t}=E$ and substituting the two new variables K and E in system (16). It follows that the equilibria are solutions of

$$\begin{aligned} T_{fp}= {\left\{ \begin{array}{ll} \begin{array}{lr} T_{fp,1}(K,E) &{} E< \bar{E}/2\\ T_{fp,2}(K,E) \quad &{}\bar{E}/2\le E< \bar{E}\\ T_{fp,3}(K,E) &{} E\ge \bar{E} \end{array} \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned}{} & {} T_{fp,1}(K,E) = {\left\{ \begin{array}{ll} \begin{array}{l} \frac{[b(1-\alpha )-a]\left( 1-d+\frac{2d}{{\bar{E}}}E\right) ^\alpha K^\alpha -a(1-\delta )\left( 1-d+\frac{2d}{{\bar{E}}}E\right) K}{\left\{ 1+\beta +\left[ \frac{4}{{\bar{E}}}E(1-\frac{E}{{\bar{E}}})+1 \right] \beta \right\} b}\beta -K=0\\ \frac{\left( {\bar{E}}^2 +1\right) E^2}{{\bar{E}} (1+E^2) }-E+\frac{ [b(1-\alpha )-a]\left( 1-d+\frac{2d}{{\bar{E}}}E\right) ^\alpha K^\alpha -a(1-\delta )\left( 1-d+\frac{2d}{{\bar{E}}}E\right) K }{\left\{ \left[ \frac{4}{{\bar{E}}}E(1-\frac{E}{{\bar{E}}})+1 \right] \beta \right\} ^{-1}\left\{ 1+\beta +\left[ \frac{4}{{\bar{E}}}E(1-\frac{E}{{\bar{E}}})+1 \right] \beta \right\} }=0\\ \end{array}, \end{array}\right. }\\{} & {} \quad T_{fp,2}(K,E) = {\left\{ \begin{array}{ll} \begin{array}{l} \frac{[b(1-\alpha )-a] K^\alpha -a(1-\delta )K}{\left\{ 1+\beta +\left[ \frac{4}{{\bar{E}}}E(1-\frac{E}{{\bar{E}}})+1 \right] \beta \right\} b}\beta -K=0\\ \frac{\left( {\bar{E}}^2 +1\right) E^2}{{\bar{E}} (1+E^2) }-E+\frac{[b(1-\alpha )-a] K^\alpha -a(1-\delta ) K }{\left\{ \left[ \frac{4}{{\bar{E}}}E(1-\frac{E}{{\bar{E}}})+1 \right] \beta \right\} ^{-1}\left\{ 1+\beta +\left[ \frac{4}{{\bar{E}}}E(1-\frac{E}{{\bar{E}}})+1 \right] \beta \right\} }=0 \\ \end{array}, \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} T_{fp,3}(K,E) = {\left\{ \begin{array}{ll} \begin{array}{l} \frac{[b(1-\alpha )-a] K^\alpha -a(1-\delta )K}{(1+ 2\beta )b}\beta -K=0\\ \frac{\left( {\bar{E}}^2 +1\right) E^2}{{\bar{E}} (1+E^2) }-E+\frac{\beta \left\{ [b(1-\alpha )-a] K^\alpha -a(1-\delta ) K\right\} }{1+2\beta }=0 \\ \end{array} \end{array}\right. }. \end{aligned}$$

(A1)

Consider system $T_{fp,1}$. The first equation has a unique solution given by

$$\begin{aligned} K^*=\left\{ \frac{\beta [b(1-\alpha )-a]\left[ \frac{(1-d){\bar{E}}+2d E}{{\bar{E}}}\right] ^\alpha }{\left( 1+\beta +\frac{4E{\bar{E}}-4E^2+{\bar{E}}^2}{{\bar{E}}^2}\beta \right) b+a(1-\delta )\left[ \frac{(1-d){\bar{E}}+2d E}{{\bar{E}}}\right] \beta }\right\} ^\frac{1}{1-\alpha } . \end{aligned}$$

(A2)

By substituting $K^*$, the second equation can be written as

$$\begin{aligned} {\mathcal {E}}(E)={\mathcal {F}}(E) \end{aligned}$$

where

$$\begin{aligned} {\mathcal {E}}(E)=E-\frac{\left( {\bar{E}}^2 +1\right) E^2}{{\bar{E}} (1+E^2) }, \end{aligned}$$

(A3)

and

$$\begin{aligned} {\mathcal {F}}(E)= b\frac{4E{\bar{E}}-4E^2+{\bar{E}}^2}{{\bar{E}}^2}* \end{aligned}$$

(A4)

$$\begin{aligned} *\left\{ \frac{\beta [b(1-\alpha )-a]\left[ \frac{(1-d){\bar{E}}+2d E}{{\bar{E}}}\right] ^\alpha }{\left( 1+\beta +\frac{4E{\bar{E}}-4E^2+{\bar{E}}^2}{{\bar{E}}^2}\beta \right) b+a(1-\delta )\left[ \frac{(1-d){\bar{E}}+2d E}{{\bar{E}}}\right] \beta }\right\} ^\frac{1}{1-\alpha }. \end{aligned}$$

Function ${\mathcal {E}}(E)$ is such that ${\mathcal {E}}(0)=0$, ${\mathcal {E}}(1/{\bar{E}})=0$, ${\mathcal {E}}(E)>0$ for $0<E<1/{\bar{E}}$ and ${\mathcal {E}}(E)<0$ for $1/{\bar{E}} <E\le {\bar{E}}/2$. The function ${\mathcal {F}}(E)$ is strictly positive for $0\le E\le {\bar{E}}/2$ therefore if any solution exists, it must lay in the interval $I=(0,1/{\bar{E}})$.

Function ${\mathcal {E}}(E)$ has a unique maximum point: being ${\mathcal {E}}^\prime (E)=1-\frac{2({\bar{E}}^2+1)E}{{\bar{E}} (1+E^2)^2}$ a value $E_m<1/{\bar{E}}$ does exist such that ${\mathcal {E}}^\prime (E)>0$ for $E<E_m$ and ${\mathcal {E}}^\prime (E)<0$ for $E>E_m$. Moreover ${\mathcal {E}}^{\prime \prime }(E)<0$ for $E\in I$.

Function ${\mathcal {F}}(E)$ is such that ${\mathcal {F}}(0)>0$ and ${\mathcal {F}}^\prime (E)>0$ being

$$\begin{aligned} {\mathcal {F}}^\prime (E)={\mathcal {F}}(E){\mathcal {G}}(E) \end{aligned}$$

with

$$\begin{aligned} {\mathcal {G}}(E)=\frac{4\left( {\bar{E}}- 2E\right) }{4 E {\bar{E}}-4E^2+{\bar{E}}^2}+\frac{2\alpha d(1-\alpha )^{-1}}{(1-d){\bar{E}} +2dE}-\frac{(1-\alpha )^{-1}\left\{ 2\beta [2b+ad(1-\delta ){\bar{E}}]-8\beta bE\right\} }{[(1+2\beta )b+a\beta (1-\delta )(1-d)]{\bar{E}}^2+{\mathcal {H}}(E)} \end{aligned}$$

and

$$\begin{aligned} {\mathcal {H}}(E)=2\beta [2b{\bar{E}}+a(1-\delta )d]E-4\beta b E^2. \end{aligned}$$

Moreover

$$\begin{aligned} {\mathcal {F}}^{\prime \prime }(E)={\mathcal {F}}\left( {\mathcal {G}}^2+{\mathcal {G}}^\prime \right) \end{aligned}$$

therefore ${\mathcal {F}}^{\prime \prime }(E)$ is negative for low values of $\alpha$ and positive otherwise, $\forall E \in (0,1/{\bar{E}})$. Since ${\mathcal {E}}(E)$ is unimodal while ${\mathcal {F}}(E)$ is strictly increasing and either convex or concave, at most two solutions $E^*_1$ and $E^*_2$ may exist that solve ${\mathcal {E}}(E)={\mathcal {F}}(E)$. Substituting the two solutions in $K^*$, for map T at most two positive fixed points $P^*_1(K^*_1,E^*_1)$ and $P^*_2(K^*_2,E^*_2)$ may exist, with $K^*_1=\left\{ \frac{\beta [b(1-\alpha )-a]\left[ \frac{(1-d){\bar{E}}+2d E^*_1}{{\bar{E}}}\right] ^\alpha }{\left( 1+\beta +\frac{4E^*_1{\bar{E}}-4(E^*_1)^2+{\bar{E}}^2}{{\bar{E}}^2}\beta \right) b+a(1-\delta )\left[ \frac{(1-d){\bar{E}}+2d E^*_1}{{\bar{E}}}\right] \beta }\right\} ^\frac{1}{1-\alpha }$, $K^*_2=\left\{ \frac{\beta [b(1-\alpha )-a]\left[ \frac{(1-d){\bar{E}}+2d E^*_2}{{\bar{E}}}\right] ^\alpha }{\left( 1+\beta +\frac{4E^*_2{\bar{E}}-4(E^*_2)^2+{\bar{E}}^2}{{\bar{E}}^2}\beta \right) b+a(1-\delta )\left[ \frac{(1-d){\bar{E}}+2d E^*_2}{{\bar{E}}}\right] \beta }\right\} ^\frac{1}{1-\alpha }$, $E^*_1<E^*_2$.

Notice that the non-hyperbolic solution in which a unique intersection exists for ${\mathcal {E}}(E)={\mathcal {F}}(E)$ has been disregarded due to its peculiarity.

Consider system $T_{fp,2}$. The first equation has a unique solution given by

$$\begin{aligned} K^\bullet =\left\{ \frac{\beta [b(1-\alpha )-a]}{\left( 1+\beta +\frac{4E{\bar{E}}-4E^2+{\bar{E}}^2}{{\bar{E}}^2}\beta \right) b+a(1-\delta )\beta }\right\} ^\frac{1}{1-\alpha }. \end{aligned}$$

(A5)

The second equation may be written as

$$\begin{aligned} {\mathcal {E}}(E)=\frac{ \left[ \frac{4}{{\bar{E}}}E(1-\frac{E}{{\bar{E}}})+1\right] \beta \left\{ [b(1-\alpha )-a] (K^\bullet )^\alpha -a(1-\delta )K^\bullet \right\} }{1+\beta +\left[ \frac{4}{{\bar{E}}}E(1-\frac{E}{{\bar{E}}})+1\right] \beta } \end{aligned}$$

(A6)

where ${\mathcal {E}}(E)$ is given by (A3). The rhs of equation (A6) is positive for $E\in [{\bar{E}}/2,{\bar{E}})$ while ${\mathcal {E}}(E)<0$ $\forall E\in [\bar{E}/2, \bar{E})$ therefore no solution exists.

Consider system $T_{fp,3}$. The first equation has a unique solution given by

$$\begin{aligned} K^\circ =\left\{ \frac{\beta [b(1-\alpha )-a]}{(1+2\beta )b+a(1-\delta )\beta }\right\} ^\frac{1}{1-\alpha }. \end{aligned}$$

(A7)

The second equation can be written as

$$\begin{aligned} {\mathcal {E}}(E) =\beta K^\circ \end{aligned}$$

(A8)

where ${\mathcal {E}}(E)$ is given by (A3). The rhs of equation (A8) is a positive constant. As function ${\mathcal {E}}(E)$ is concerned, it has ${\mathcal {E}}(\bar{E})=0$, $\lim _{E\rightarrow +\infty }{\mathcal {E}}(E)=+\infty$, ${\mathcal {E}}^\prime >0$, therefore equation (A8) always has a unique solution $E^\circ >\bar{E}$.

It follows that map T has one fixed point $P^{\circ }=(K^{ \circ },E^{\circ })$.

Appendix B Stability of the fixed points

For $E<1/{\bar{E}}$, the stability of the fixed points depends on the solutions of the characteristic polynomial

$$\begin{aligned} \begin{array}{rl} \lambda ^2-(\Psi _{EE}+\Psi _{KK})\lambda +\Psi _{EE}\Psi _{KK}-\Psi _{KE}\Psi _{EK}&=0. \end{array} \end{aligned}$$

defined in (19). Analytical solutions are difficult to find, therefore we proceed with numerical simulations as follows: after establishing the values of the parameters and moving a and b, we define the value of $K^{*}$ defined in equation (A2) as a function of $E_t$. We then substitute it into the equation of $E_{t+1}$ and numerically search for the solutions of $E_{t+1}=E_t$. As a result, we obtain the values of K and E in the fixed point thanks to which it is possible to numerically identify the roots of the characteristic polynomial. Regarding the fixed points in the region $E<1/{\bar{E}}$ we observe that:

• Moving d does not modify the qualitative behavior of the fixed points;

• The fixed point $P^{*}_{1}$ is always stable;

• When $\alpha$ is high, the fixed point $P^{*}_{2}$ is stable.

• When $\alpha$ assumes intermediate levels (but above 0.5), the stability of the fixed point $P^{*}_{2}$ varies: in case $\beta$ and $\delta$ are low, the fixed point is stable if b is low and a is high and unstable otherwise;

• Increasing $\beta$ reduces the region in which $P^{*}_{2}$ is stable;

• When $\alpha$ assumes low levels, the stability of fixed point $P^{*}_{2}$ depends on the combination of all the parameter values, and nothing can be said a priori.

With regards to the region in which $E>{\bar{E}}$ it has been proved in the paper that $P^{ \circ }$ is stable.