1 Introduction

Formally, a decision can be defined as a choice made based on available information; decision-making, therefore, also involves the choice of a method aimed at solving a specific decision problem (Greco et al., 2016).

Multi-Criteria Decision-Making (MCDM) is a sub-domain of Operational Research dealing with problems that explicitly evaluate alternatives against a set of criteria. The complexity of those problems originates from the presence of multiple, and often conflicting, criteria. Also, decision makers (in the following, also DMs) might have different preferences.

It is known that the MCDM field can deal with different types of problems faced by DMs, such as choice, sorting, description and ranking. The choice problem consists of a situation in which the DMs have to select, within a set of alternatives, a subset being considered as the best. A sorting problem implies the assignment of each alternative to predefined ordered categories. The description problem consists of the identification of important features of the alternatives. The ranking problem concerns generating a partial or complete order of alternatives.

In order to deal with the inherent complexity of such problems, and with their variety, many MCDM methods have been developed.

Examples of the most popular methods belonging to the European school are the ELECTRE (ÉLimination et Choix Traduisant la REalité) (Roy, 1968), PROMETHEE (Preference Ranking Organization Method for Enrichment of Evaluations) (Brans, 1982) and DRSA (Dominance Rough Sets Approach) (Greco et al., 2001) methods families. Such methods are based on outranking relations.

The common MCDM methods belonging to the American school include VIKOR (VlseKriterijumska Optimizacija I Kompromisno Resenje) (Opricovic & Tzeng, 2007), AHP (Analytic Hierarchy Process) (Golden et al., 1989), and COPRAS (Complex Proportional Assessment) (Zavadskas et al., 1994). These methods are based on a functional approach, defining a synthetic measure of value.

The theory of value functions aims at assigning a number to each alternative in such a way that the DM’s preference order of the alternatives is the same as the order of the numbers associated with the alternatives. The value associated to an alternative is a monotonic function against evaluations across criteria. In terms of preferences, the evaluation of an alternative becomes the sum of marginal value functions. The Simple Additive Weighting (SAW) method is an example of the last class of methods where marginal value functions are identities. In the SAW method, the value of an alternative is equal to the weighted sum of its evaluation ratings. Another method based on the value function approach in MCDM is TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution). It is an MCDM method originally developed by Hwang and Yoon (1981) with further refinements by Yoon (1987) and Hwang et al. (1993). TOPSIS methods require the independence of criteria for being utilised real-life (Behzadian et al., 2012). However, independence of criteria is hard to be guaranteed in real applications (Antuchevičiene et al., 2010); as such, TOPSIS methods might produce biased rankings (Gershon, 1984; Sureeyatanapas et al., 2018). TOPSIS is based on the fundamental idea that the best alternatives should have the shortest distance from the positive ideal solution (PIS) and the longest distance from the negative ideal solution (NIS). Such ideal solutions might not correspond to any existing alternative, as they are artificially obtained combining strengths (for the PIS) and weaknesses (for the NIS) displayed by all the actually existing solutions. While the TOPSIS approach is not challenging to be implemented, it still requires more computational effort than SAW (Hamdani & Wardoyo, 2016). Also, it has been shown that TOPSIS methods suffers from the rank reversal phenomenon, which does not affect SAW approaches (García-Cascales & Lamata, 2012). Within its general structure, several variants have been introduced for the TOPSIS method, concerning several steps of its procedure, including: the normalisation of ratings (Gershon, 1984; Senouci et al., 2016; Zavadskas et al., 2006; Zardari et al., 2015; Hu et al., 2016; Harris et al., 2020), the calculation of distances among alternatives (Huang et al., 2009; Chang et al., 2010; Vega et al., 2014; Shyur et al., 2015; Li, 2009; Garg & Kumar, 2020), the value function to calculate the final scores of alternatives (Lai et al., 1994; Doukas et al., 2010; Opricovic & Tzeng, 2004; Ren et al., 2007; Kuo, 2017).

TOPSIS and SAW methods have been often used in combination and their rankings have been compared for the sake of decision-making problems in multiple scientific fields (Chu et al., 2007; Savitha & Chandrasekar, 2011; Seyedmohammadi et al., 2018; Bhaskar & Kudal, 2019; Firgiawan et al., 2020; Wardana et al., 2020; Meshram et al., 2020; Dobrovolskiene & Pozniak, 2021; Vakilipour et al., 2021; Vassoney et al., 2021). The above-mentioned works share some common characteristics. TOPSIS is often adopted in its original form and the adopted separation measure is the Euclidean distance. Moreover, the literature concerning applications has failed to reach a consensus on the differences between rankings produced by TOPSIS and SAW methods. In fact, some applications highlight that rankings can be extremely different (Wardana et al., 2020; Dobrovolskiene & Pozniak, 2021), while others stress the high similarity in the produced results (Chu et al., 2007).

Despite the availability of multiple MCDM methods, no method is universal and can be considered as appropriate for use in every decision-making situation (Roy, 1996; Velasquez & Hester, 2013). Therefore, using different multi-criteria methods may lead to different decision recommendations (Zanakis et al., 1998). As such, the choice of a decision support method which is appropriate to a given problem becomes an important issue, as only an adequately chosen method allows one to obtain a correct solution reflecting the preferences of DMs (Cinelli et al., 2020). For instance, formal approaches have been developed to identify a subset of MCDM methods suitable for specific types of problems (Zak, 2005; Hajkowicz & Higgins, 2008; Sabaei et al., 2015; Scholten et al., 2017; Wkatrobski et al., 2019a, b; Kaya et al., 2019; Yannis et al., 2020; Kolios et al., 2016; Sarraf & McGuire, 2020). The effort of shaping MCDM methods for the sake of applications encouraged scholars to develop the so-called class of hybrid MCDM methods. Hybridisation of MCDM methods has been recognised after the works of Shyur and Shih (2006), Tzeng et al. (2007) and Liao et al. (2014). Following the work of Zavadskas et al. (2016), hybrid approaches to MCDM can be categorised in four groups. The first group deals with the utilisation of more than one MCDM method and the integration of results for final decision-making. The second suggests solving two tasks, such as determining criteria weights and performance values and integrating them into a multi-attribute utility function value. The third suggests the utilisation of fuzzy theory in the decision-making process. This latter often stems from a context of uncertainty, when ambiguities make reaching a proper decision difficult. The fourth is the integration of MCDM methods with different techniques, especially from statistics and optimisation.

Summing up the above considerations on the literature related to MCDM applications, it is worthy to investigate hybrid procedures that approximate TOPSIS methods to the marginal value functions approach included in SAW. In the current paper, the key idea is whether hybridisation can be obtained through one of internal functions in TOPSIS methods: distances or separation metrics from ideal alternatives. It is not a case that Kizielewicz et al. (2021) study the effects of different distances in TOPSIS methods on rankings. In this paper, the Euclidean and Manhattan distances were compared, while obtained rankings were compared with some sophisticated similarity coefficients to check their correlation. They show that used distance metric has an important impact on the results and rankings are significantly different.

Beside the Euclidean distance, Tchebychev and Manhattan distances are traditionally accepted in MCDM literature and they have a relatively easy mathematical formulation that can be captured by DMs (Olson, 2004; Vega et al., 2014). Nevertheless, more sophisticated distances can be utilised in TOPSIS methods but many of them cannot be easily interpreted by DMs (Anandan & Uthra, 2017).

The current work clarifies how similarities between TOPSIS and SAW are shaped across the above distances and, especially, through the multiple lenses of DMs preferences. The rest of this paper is organised as follows.

Section 2 presents a review of literature on benchmarks across MCDM methods, with a particular and more pertinent reference to TOPSIS and SAW methods. More specifically, we focus on works that use a simulation approach to the problem of benchmarking MCDM methods or that utilise specific similarity techniques to compare rankings. Section 3 provides fundamental notions for SAW and TOPSIS methods, with a specific reference to the formal properties of TOPSIS methods related to additivity and trade-off weights. Section 4 provides the settings of our experiment including how we measure DMs’ preferences through similarity coefficients. Section 5 analyses the outcomes of the experiment. Section 6 includes a note on the phenomenon of rank reversals for TOPSIS methods. Section 7 summarises the findings of this work, especially against DMs preferences; suggestions for future researches are provided. Numerical results of the experiments are provided and are attached to the current paper as supplementary information.

2 Literature review

Comparisons among MCDM methods have been traditionally focusing on their accuracy. If different MCDM methods achieve contradictory results, then the correctness of the recommendations provided by each of them must be carefully discussed (Olson, 2004; Chang et al., 2013). Different MCDM methods may produce different rankings of alternatives: however such different methods require different levels of computational efforts. In other words, if a simple method produces similar rankings of alternatives to the ones provided by more complex approaches, using the simplest method can save computational time and efforts without affecting the accuracy of the solution (Saaty & Ergu, 2015). However, a very common practical problem is the one of finding a reference method, against which results (scores, ranks, best selection) can be compared. For instance, SAW is the reference method utilised in the seminal work of (Zanakis et al., 1998), due to its inherent simplicity.

In the literature, authors have proposed comparisons between a plethora of MCDM methods, including TOPSIS and SAW. Zanakis et al. (1998) deal with comparison issues where few alternatives are evaluated against a larger number of criteria. The study conducts comparisons of final scores and associated rankings for a wide range of MCDM methods. Comparisons are made through an extensive series of similarity coefficients (performance measures, in the authors’ own language). They utilise different probabilistic distributions for the subsets of weights and ratings, in order to generate decision matrices for testing the studied aggregation methods.

Parkan and Wu (2000) compare the final scores obtained by the MCDM method called OCRA (operational competitiveness rating analysis) with the results of AHP and Data Envelopment Analysis (DEA) in order to understand their differences. The authors do not use similarity coefficients to perform their analysis, as this is performed on a specific selection problem.

Chen (2012) employs a SAW method and TOPSIS as the main structures to deal with interval-valued fuzzy evaluation information; SAWand TOPSIS-based aggregations are employed, and a comparative study is conducted through computational experiments. computational experiments. Except for some specific cases, the results show that interval-valued fuzzy SAW and TOPSIS methods produce almost the same preference structures because of the very similar ranking orders of the alternatives. The similarity of top ranked alternatives, in most of the experimental cases, is high.

Selmi et al. (2016) compare multiple MCDM methods such as ELECTRE III, PROMETHEE I and II, TOPSIS, AHP and PEG. The authors look at two case studies in which a certain number of Pareto-optimal alternatives are obtained. A Gini index is adopted in order to quantify the dispersion of Pareto optimal alternatives in rankings.

Zamani-Sabzi et al. (2016) compare a plethora of fuzzy MCDM methods including TOPSIS and SAW, but also, inter alia, four AHP variants, VIKOR and ELECTRE. Triangular fuzzy numbers are employed for composing decision matrices. Zamani-Sabzi et al. (2016) are interested in detecting statistical significance of their correlation analysis and in measuring the magnitude of the utilised rank correlation coefficients. They investigate similarities in rankings through Kendall’s tau-b and Spearman’s rho tests. The authors deal with decision-making situations in which the number of alternatives and criteria are similar, up to a maximum of 15. Authors find out that as the number of criteria increases, similarity tends to decrease; as the number of alternatives increases, similarity tends to increase. The result is, statistically speaking, interesting for the increase of alternatives, as it is well-known that Kendall’s tau and Spearman’s rho coefficients’ thresholds decrease as the number of observations increases (with a fixed level of statistical significance) (Zar, 1972).

Shekhovtsov and Sałabun (2020) examine differences in rankings obtained using TOPSIS and VIKOR methods. For this purpose, authors apply classical versions of TOPSIS and VIKOR methods to randomly generated decision matrices with different criteria and alternatives. Then, authors compare obtained rankings by using three similarity coefficients. Specifically, they utilise Spearman’s rank correlation coefficients (both in the classic and weighted form) and rank similarity coefficients. Similar coefficients are also utilised in a recent work of Shekhovtsov et al. (2021) where authors compare rankings obtained by six MCDM methods, including TOPSIS, for a specific decision-making problem in the context of green economy. The same coefficients are utilised in the very comprehensive work of Sałabun et al. (2020). Authors provide a reference set of MCDA methods TOPSIS, VIKOR, COPRAS, and PROMETHEE II. The authors utilise Spearman’s correlation and rank similarity coefficients; matrices with different number of criteria and alternatives are processed. The number of criteria varies from two to five and the number of the alternatives belongs to the set \(\{3, 5, 10, 50, 100\}\). For each of the 20 combinations, the numbers of alternatives and criteria are generated after random decision matrices. The authors aim to build a complex benchmarking model. Performed analysis and benchmarking methods include various weighing methods such as entropy and standard deviation methods and several techniques of normalisation of ratings.

2.1 Contribution of the study

While the body of literature devoted to the comparison of the performances of MCDM methods is growing in scope, there is a lack of studies specifically focused on the performances of the TOPSIS method, and on its added value compared to simple SAW approaches. As such, in this study, we randomly generate criteria weights and alternatives’ ratings for each criteria; then, we calculate rankings of alternatives by applying TOPSIS and SAW methods. Ratings are randomly extracted, criterion by criterion. Initial ratings do not present any dependence and ratings and criteria weights are evenly distributed. We assume that the number of alternatives is larger than the number of criteria following the recent work of Sałabun et al. (2020). As regards the TOPSIS method, we assess its performance, in comparison to a SAW approach, by adopting and comparing different distances (i.e., Euclidean, Manhattan and Tchebychev distances). Rankings are compared by using above-mentioned similarity coefficients discussed in the literature review. In order to perform a systematic comparison, we employ the widest possible range of similarity coefficients. In particular, similarities are measured through nine coefficients that capture DMs’ preferences in terms of top selections, distances in final rankings, and inversions of ranks.

3 MCDM methods with trade-off weights and value functions: SAW and TOPSIS

The set of alternatives can be indicated as Z. The number of alternatives can be defined as m. The set of criteria (or attributes) is C. The number of criteria is n. For some MCDM methods, compensation refers to the existence of trade-offs, i.e. the possibility of offsetting a disadvantage on some attribute by a sufficiently large advantage on another attribute. Weights \(w_{j}\ge 0\) for each criterion j represent the trade-offs in the decision-making processes. J and \(J^{'}\) are the subsets of positive and negative criteria, respectively. Ratings (alternatively, referred to as judgments or valuations) of an alternative i with respect to criterion j are represented by \(x_{ij}\). An \(m\times n\) matrix \((x_{ij})_{m\times n}\) (or simply \(x_{ij}\)) is built and summarises the valuations of decision-makers on alternatives.

The first step transforms the various ratings, which might be expressed in different reference units, into non-dimensional attributes, thus allowing comparisons across criteria. Normalisation techniques might be applied to the matrix \(x_{ij}\). Several techniques for normalisation are available in the literature such as the minimum-maximum method or the maximum method, the sum method, the vector method (Sałabun et al., 2020). Therefore, a new matrix of normalised ratings \((r_{ij})_{m\times n}\) (or simply \(r_{ij}\)) is built.

Aggregation techniques produce, in different ways, the final scores for alternatives in Z. Both SAW and TOPSIS methods utilise a value function approach. The preference of the DM can be represented by a value function if there is a function U which associates a value or a score to each alternative in such a way that \(U(i) \ge U(k)\) whenever the DM prefers i to k. The preference relation (built using the value function approach) is, then, a weak order, i.e., a complete and transitive relation. Using such information it is not difficult, in general, to elaborate recommendations. The definition of aggregation functions may not always be simple, however. We discuss how aggregation or value functions are built for SAW and TOPSIS methods.

3.1 SAW method

Under some conditions, among which preferential independence (see Keeney et al. (1993), p. 110), such a preference relation can be represented by means of an additive value function. Let i be an alternative in Z. Let R be the space of ratings for each single criterion. There are n functions \(u_{j}:R \rightarrow \mathbb {R}\) such that the value function can be expressed as follows:

$$\begin{aligned} U(i)=\sum _{j=1}^{n} w_{j} u_{j}(r_{ij}). \end{aligned}$$

Each function \(u_{j}\) is defined on the space of valuations for criterion j and is increasingly monotonic, if criterion j is positive, or decreasingly monotonic, if criterion j is negative. Trade-off weights are usually normalised, that is \(\sum _{i=1}^{n}w_{j}.\) The additive method is said to be simple if marginal functions are identities. The final score of alternative i for SAW method is, then, computed as follows:

$$\begin{aligned} U(i)=\sum _{j=1}^{n} w_{j} r_{ij}. \end{aligned}$$

3.2 TOPSIS method

The procedure of the TOPSIS methods is articulated in the following 4 steps.

  1. 1.

    A \(m\times n\) matrix \((v_{ij})_{m\times n}\) (or simply \(v_{ij}\)) is built with the generic element of this new matrix being: \(v_{ij}=w_{j}r_{ij}.\)

  2. 2.

    Let \(v_{j}^{*}=\max _{i=1..m} v_{ij}\) if \(j\in J^{+}\) and \(v_{j}^{*}=\min _{i=1..m} v_{ij}\) if \(j\in J^{-}\) be the quantities for \(j=1, \ldots ,n\). The vector \(v^{*}=(v_{j}^{*})_{j=1\ldots n}\) is the so-called (positive) Ideal Solution (IS). Let \(v_{j}^{**}=\min _{i} v_{ij}\) if \(j\in J^{+}\) and \(v_{j}^{*}=\max _{i} v_{ij}\) if \(j\in J^{-}\) be the quantities for \(j=1, \ldots ,n\). The vector \(v^{**}=(v_{j}^{**})_{j=1\ldots n}\) is the so-called negative ideal solution (NIS).

  3. 3.

    Distances between each alternative i and both an ideal solution (IS) and a negative ideal solution (NIS) are calculated. We present the three utilised distances:

    • Euclidean Distance. The Euclidean distance between a generic alternative i and IS or NIS are as follows, respectively:

      $$\begin{aligned}&S_{i}^{*}=\sqrt{\sum _{j=1}^{n} (v_{j}^{*}-v_{ij})^{2}}&S_{i}^{**}=\sqrt{\sum _{j}^{n} (v_{j}^{**}-v_{ij})^{2}} \end{aligned}$$

    • Manhattan distance. The distance between two points is the sum of the absolute values of the difference of their respective Cartesian coordinates. The Manhattan metric is also known as snake distance or city block distance. The Manhattan distance between an alternative i and the IS or NIS becomes the following, respectively:

      $$\begin{aligned}&S_{i}^{*} =\sum _{j=1}^{n} \mid v_{j}^* - v_{ij} \mid&S_{i}^{**}=\sum _{j=1}^n \mid v_{j}^{**}-v_{ij} \mid \end{aligned}$$

    • Tchebychev distance. In this geometry, the distance between two points is the maximum of the absolute values of the differences between their respective Cartesian coordinates. The distance between an arbitrary alternative i and the IS or NIS becomes the following, respectively:

      $$\begin{aligned}&S_{i}^{*} =\max _{j=1..n} \mid v_{j}^{*} - v_{ij} \mid&S_{i}^{**} = \max _{j=1..n} \mid v_{j}^{**}-v_{ij} \mid \end{aligned}$$
  4. 4.

    The aggregated value of alternative i for TOPSIS methods is defined as follows:

    $$\begin{aligned} U(i)=\frac{S_{i}^{**}}{S_{i}^{**}+S_{i}^{*}}. \end{aligned}$$

Final scores of alternative i for SAW and TOPSIS methods are between 0 and 1. Alternatives are, then, ranked by ascending order of final scores.

3.3 Formal properties

Both methods are based on trade-offs among criteria and on the value function approach. Rankings produced by TOPSIS methods and SAW (across distances) are affected by different ratings and trade-off weights. Therefore, potential similarities between the two methods might be related to formal properties (shared by methods) involving the behaviour of value functions if trade-off weights or ratings change. We, therefore, propose some formal properties; we carefully analyse, comment and highlight the effects of these properties with reference to the experimental comparisons performed in our study. However, some choices must be done at the level of the analysis of formal properties. In fact, it is assumed that all the criteria in C are positive and trade-off weights \(w_{j}\) are in the interval [0, 1] and initial ratings \(r_{ij}\ge 0\) are just positive numbers (not necessarily normalised). Most current choices match with the settings of our experiment.

More specifically, our proposed formal properties do not want to deal with the formation process of ratings and trade-off weights but, simply, with the aggregation process. Therefore our analysis does not take into account normalisation techniques occurring before the aggregation processes.Throughout the rest of the current Section, ratings, normalized ratings or decision matrix can be assimilated.

The proposed formal properties can be adapted to any type of MCDM methods based on the value function approach and with trade-offs among criteria. Our analysis formalises the existence of ratings and weights (it does not matter if they are normalised or not). As such, our analysis keeps a level of generality which goes beyond the specific application.

3.3.1 Additive properties

Formal properties, taking into account the randomness of ratings (that is \(r_{ij}\ge 0\)) of alternative i, against criterion j are studied. Trade-off weights \(w_{j}\) are assumed to be given for each criterion j. The additive structure in ratings consists in adding two decision matrices \(r_{ij}\) and \(r_{ij}'\). For instance, the decision matrix can be multiplied by trade-off weights, that is \(v_{ij}=w_{j}r_{ij}\) (as it has been done in STEP 1 of TOPSIS methods). Similarly, we define \(v_{ij}':=w_{j}r_{ij}'\). Once trade-off weights are uniquely given, the difference between \(r_{ij} + r_{ij}'\) and \(v_{ij}+v_{ij}'=w_{j}(r{ij} + r{ij}')\) is conceptually marginal. We will often exchange their roles through Properties 1–3 and Propositions 1–3, without generating ambiguity.

We are ready to utilise the sum of decision matrices, that is \(r_{ij} + r_{ij}'\) as an input into the aggregation procedures of MCDM methods. It is necessary to distinguish between the aggregation process operated having ratings \(r_{ij} + r_{ij}'\) and the aggregation process operated having ratings \(r_{ij}\). To be parsimonious with extra notations, further symbols used in the aggregation processes are denoted by the additional superscript \('\) if the decision matrix is \(r_{ij} + r_{ij}'\) and are denoted without the superscript if the utilised decision matrix is \(r_{ij}\). The following property is presented for the above MCDM methods.

Property 1

Let U be the value function of an MCDM method. For any pair \(v_{ij},v_{ij}'\) the following condition:

$$\begin{aligned} U^{'}(i) = U(i) + a(i) \sum _{j=1}^{n} v_{ij}', \quad i\in Z, \quad a(i)\in \mathbb {R}. \end{aligned}$$
(1)

holds.

Property 1 requires that the difference of the value function (aggregating \(v_{ij} + v_{ij}'\)) and the value function (aggregating \(v_{ij}\)) is equal to an additive formulation of terms \(v_{ij}'\) over the set of criteria. Moreover, Property 1 requires that the such additive piece is readjusted by term a(i). It remains implicit that term a(i) may still depend on terms \(v_{ij}\) or on other parameters of MCDM problems such as the number of alternatives or the number of criteria.

Proposition 1

SAW satisfies Property 1.

Proof

Formula 1 is satisfied for SAW by choosing \(a(i)=1\) for each alternative. \(\square \)

TOPSIS is not an additive MCDM method. However, certain distances might produce similar additive effects in TOPSIS methods (weaker, however, than Property 1). For instance, if TOPSIS is endowed with an Euclidean distance, the value function has no additive property. We propose the following definition that is useful to our settings.

Property 2

For any given \(r_{ij}\), then there exists a decision matrix, let’s say \(r_{ij}'\) (depending on \(r_{ij}\)), such that the value function U still satisfies formula (1).

Proposition 2

TOPSIS with the Manhattan distance satisfies Property 2.

Proof

From recalling Step 2 of TOPSIS methods, we define the following subsets: \(A_{j}=\{ i \in Z \,: \, v_{ij}=v_{j}^{*}\}\) and \(B_{j}=\{ i \in Z \,: \, v_{ij}=v_{j}^{**} \}\) for \(j\in C.\) We define the matrix \(r_{ij}'\) as follows. If \(i\in A_{j} \cup B_{j}\), then \(r_{ij}':=0\). If \(i \not \in A_{j} \cup B_{j} \) we define \(r_{ij}'\) such that the following inequalities:

$$\begin{aligned} v_j^{**}< w_{j} (r_{ij}' + r_{ij})<v_j^{*} \end{aligned}$$

hold. From the above definitions it straightforwardly follows that \({v_j^*}'=v_{j}^*\) and \({v_j^{**}}'=v_{j}^{**}\). We calculate the distances of alternatives (having ratings rij + rij\('\)) by employing the Manhattan metric, and we obtain the following equalities:

$$\begin{aligned} {S_i^*}' =S_i^* - \sum _{j=1}^{n} v_{ij}', \quad {S_i^{**}}'=S_{i}^{**} + \sum _{j=1}^{n} v_{ij}'. \end{aligned}$$

The value function aggregating ratings \(r_{ij}+r_{ij}'\) is, then, equal to

$$\begin{aligned} U^{'}(i)=\dfrac{{S_i^{**}}'}{{S_i^{**}}'+ {S_i^{*}}'}= \dfrac{S_i^{**}+ \sum _{j=1}^{n} v_{ij}^{'}}{{S_i^{**}}' +\sum _{j=1}^{n} v_{ij}' +{S_i^*}-\sum _{j=1}^{n} v_{ij}'}= \\ =\dfrac{S_{i}^{**}}{S_{i}^{**} +S_{i}^{*}} + \dfrac{1}{S_{i}^{**} +S_{i}^{*}}\sum _{j=1}^{n} v_{ij}'=U(i)+ a(i)\sum _{j=1}^{n} v_{ij}'. \end{aligned}$$

Formula (1) is satisfied for TOPSIS with the Manhattan distance by taking \(a(i):=\dfrac{1}{S_{i}^{**} +S_{i}^{*}}\). \(\square \)

The proof of Proposition 2 provides the existence of matrices \(r_{ij}'\) for which Proposition itself holds. Interestingly, as the number of alternatives largely exceeds the number of criteria, \(r_{ij}'\)s tends to assume value 0 for few alternatives i. This implies that matrices \(r_{ij}'\) are not too specific and match with the randomness of ratings in our experimental settings. A further refinement of the previous additive properties is defined for the sake of our analysis; it is weaker than Property 2 and, then, weaker than Property 1. Finally, we provide a result for TOPSIS methods.

Property 3

For any given \(r_{ij}\) decision matrix, there exists a decision matrix, let’s say \(r_{ij}'=r_{i}'\), such that the value function U still satisfies formula (1).

Proposition 3

Assume that weights \(w_{j}\) are constant for each criterion. TOPSIS with the Tchebichev distance satisfies Property 3.

Proof

We define \(r_{ij}'\) (or \(v_{ij}'\) if one may prefer) as we have done in the proof of Proposition 2. In addition, we assume that ratings \(r_{ij}'=r_{i}'\). Hence, it follows that \(v_{ij}'= w_{j}r_{i}'=w r_{i}'=v_{i}'\). We utilise the Tchebichev distance to calculate the distances in TOPSIS methods and we obtain the following equalities:

$$\begin{aligned} {S_i^*}'={S_i^*} - v_{i}', \quad {S_i^{**}}'=S_{i}^{**} + v_{i}'. \end{aligned}$$

The final value aggregating ratings \(r_{ij}+r_{i}'\) is calculated:

$$\begin{aligned} U'(i)=\dfrac{{S_i^{**}}'}{{S_i^{**}}'+ {S_i^*}'}= \frac{S_{i}^{**}}{S_{i}^{**} +S_{i}^{*}} + \frac{1}{S_{i}^{**} +S_{i}^{*}} v_{i}'=U(i)+ \frac{1}{S_{i}^{**} +S_{i}^{*}}v_{i}' \end{aligned}$$

Formula (1) is satisfied for TOPSIS with the Tchebichev distance by taking \(a(i):=\dfrac{1}{n(S_{i}^{**} +S_{i}^{*})}\). \(\square \)

The hypotheses of Proposition 3 tells us that trade-off weights are constant. This means that TOPSIS, endowed with the Tchebichev distance, satisfies Property 3 with the help of a strong hypothesis.

3.3.2 Trade-off sensitivity

Further formal properties, which takes into account the randomness of trade-off weights, are studied. It is assumed that ratings are considered fixed. When referring to MCDM methods, trade-off sensitivity usually refers to the behaviour of the value function in response to changes in trade-off weights. For the sake of a simple analysis, the following assumption is made: trade-off weights \(w_{j}\) are distinct from 0, 1. We present the definition of trade-off sensitivity.

Property 4

Let be the value function of an MCDM method. Let \(w_{j}\) be trade-off weights. For each \(i\in Z\), for each \(j \in C\) there exists a neighbourhood \(I \subset ]0,1[\) of weight \(w_{j}\) such that the value function is strictly monotonic on I.

The above notion requires that it is possible to (strictly) decrease or increase the value of an alternative if a trade-off weight slightly and unilaterally changes. With an abuse of notations, we denote with superscript \('\) the quantities for TOPSIS and SAW methods (as described in Sub Section 3.2), if the utilised trade-off weight is \(w_{j}'\) (replacing \(w_{j}\)). Considering that weights unilaterally change in our discussion, we are convinced that this abuse of notations does not create ambiguity throughout the rest of Section. Some results are provided for TOPSIS methods and SAW.

Proposition 4

Assume that ratings \(r_{ij}\) are strictly positive for each criterion j and for each alternative i. Then, SAW satisfies Property 4.

Proof

Let \(w_s\) be the vector collecting trade-off weights. Let j be a specific criterion with the associated weight \(w_{j}\). Let be an alternative i and a specific criterion \(j\in C\). Consider the value function calculated for the alternative i as a function of criterion variable \(w_{j}\) as follows: \(U(i): ]0,1[ \rightarrow \mathbb {R}\). As such, U(i) is differentiable and take the first derivative, that is the following:

$$\begin{aligned} \dfrac{\partial U(i)}{\partial w_{j}}=r_{ij}>0. \end{aligned}$$

Then, there exists an open neighbourhood I of \(w_{j}\) such that U(i) is strictly increasing on I since \(w_{j}\not =0,1\). \(\square \)

Proposition 5

Assume that the following conditions are satisfied for each \(i\in Z\):

  • \(v_{s}^{*}\not =v_{is}\) and \(v_{is'}\not =v_{s'}^{**}\) for some criteria \(s,s'\in C\);

  • \(\frac{{S_i^*}}{{S_i^{**}}} (v_{ij}-v_{j}^{**})^2\not =\frac{{S_i^{**}}}{{S_i^*}} (v_{j}^{*}-v_{ij})^2\) for each criterion \(j\in C\).

Then, TOPSIS endowed with the Euclidean distance satisfies Property 4.

Proof

Let \(w_s\) be the vector collecting trade-off weights. Let i be an alternative. Let j be a specific criterion with the associated weight \(w_{j}\). Consider the following three functions: \(S_i^{*},S_i^{**},U(i): ]0,1[ \rightarrow \mathbb {R}\) as a function of criterion-variable \(w_{j}\). From the first hypothesis it follows that functions \(S_i^{*},S_i^{**}\) are non-null in \(w_{j}\). This implies that \(S_i^{*},S_i^{**}\) are derivable with respect to variable \(w_{j}\). As such, U(i) is differentiable and take the first derivative of the value function, that is the following:

$$\begin{aligned} \dfrac{\partial U(i)}{\partial w_{j}}=-\dfrac{S_i^*}{(S_i^*+S_i^{**})^2} \dfrac{ (v_{ij}-{v_j}^{**})^2}{w_{j} \, S_i^{**}} +\dfrac{S_i^{**}}{(S_i^*+S_i^{**})^2} \dfrac{ (v_{ij}-{v_j}^{*})^2}{w_j S_i^{*}}. \end{aligned}$$
(2)

The quantity (2) is non-null because of the second hypothesis. The thesis follows as in the proof of Proposition 4. \(\square \)

Proposition 6

Assume that the following condition is satisfied:

$$\begin{aligned} {S_i^*} (v_{ij}-v_{j}^{**})\not ={S_i^{**}} (v_{j}^{*}-v_{ij}) \quad i\in Z, j\in C. \end{aligned}$$

Then, TOPSIS endowed with the Manhattan distance satisfies Property 4.

Proof

The proof is very similar to the one of Proposition 5, and we leave it to the reader. \(\square \)

For Tchebychev distance in TOPSIS methods, the following two subsets are defined: \(\arg _{j\in C} S_{i}^{*}, \; \arg _{j\in C} S_{i}^{**}\subset C\). In fact, they are the subsets of criteria at which the maximum values \(S_{i}^{*}\),\(S_{i}^{**}\) are attained, respectively (in Step 3).

Proposition 7

Assume that the following condition is satisfied:

$$\begin{aligned} \arg _{j\in C} S_i^{*} \cup \arg _{j \in C} S_i^{**}\not = C, \quad i\in Z. \end{aligned}$$

Then, TOPSIS endowed with Tchebichev distance does not satisfy Property 4.

Proof

Let \(w_s\) be the vector collecting trade-off weights. Let i be an alternative. From the main assumption it follows that there exists \(j\in C\) such that the following inequalities:

$$\begin{aligned} S_i^{*}> v_{j}^{*} - v_{ij}\ge 0 \quad S_i^{**}> v_{ij} - v_{j}^{**} \ge 0 \end{aligned}$$
(3)

are true. Hence, it follows that \(S_i^{*}, S_i^{**}>0\). We denote the previous differences with the following symbols: \(\epsilon ^{*}= S_i^{*} - (v_{ij}-v_{j}^{*})>0, \, \epsilon ^{**}= S_i^{**} - (v_{j}^{**}-v_{ij})>0.\) Consider the following three functions \(v_{ij}, v_{j}^{**},v_{j}^{*}: ]0,1[ \rightarrow \mathbb {R}\) as functions of criterion-variable \(w_{j}\).From simple continuity arguments for the above three functions, it follows that there exist two neighbourhoods \(I^{*}, I^{**} \subseteq ]0,1[\) of \(w_{j}\) such that

$$\begin{aligned}{} & {} \mid (v_{j}^{*'} - v_{ij}') - (v_{j}^{*} - v_{ij})\mid<\epsilon ^{*} \quad w_{j}'\in I^{*} \\{} & {} \mid (v_{ij}'-v_{j}^{**'} ) - (v_{ij}- v_{j}^{**}) \mid <\epsilon ^{**} \quad w_{j}'\in I^{**}. \end{aligned}$$

Let us define \(I=I^{*} \cap I^{**} \). Then, the above inequalities are true if \(w_{j}' \in I\). From simple calculations, it follows that the hand-right side of inequalities in (3) can be written with weights \(w_{j}'\in I\) (including the former weight \(w_{j}\)), that means the following:

$$\begin{aligned} S_i^{*}> v_{j}^{*'} - v_{ij}' \quad S_i^{**}> v_{ij}' - v_{j}^{**'}. \end{aligned}$$
(4)

Thanks to the fact that the only variation in \(w_{s}\) occurs only for the weight \(w_{j}\), formula (4) tells us that \(S_i^{*'}=S_i^{*}\) and \(S_i^{**'}=S_i^{**}.\) Thanks to definition of the value function in TOPSIS (in Step 4), this implies \(U^{'}(i)=U(i)\) if \(w_{j}'\in I\). Summing up, we have proved that for each alternative \(i\in Z\) there exists a criterion \(j\in C\) and there exists a neighbourhood I of \(w_{j}\) such that the value \(U'(i)\) does not change if \(w_{j}'\in I.\) Then, the previous sentence contradicts Property 4. \(\square \)

At a first glance, it is straightforward to say that hypotheses of Propositions 4, 5, 6 and 7 can be considered generic against the randomness of trade-off weights and ratings.

3.3.3 Similarities through formal properties

Summing up results (with their specific hypotheses) and comments on the proposed formal properties for the two MCDM methods, an interpretative map displaying the closeness of each method to the above formal properties is proposed in Table 1. Indeed, Table 1 provides an heuristic and qualitative comparison among TOPSIS methods (endowed with the three different Minkowski distances) and SAW.

Table 1 Additive properties and trade-off sensitivity across methods
Full size table

Table 1 shows how similarities between rankings produced by TOPSIS methods and SAW might be distributed across distances. It clearly appears that TOPSIS, endowed with the Manhattan distance, satisfies properties that are the closest to the ones of SAW. For instance, trade-off sensitivity decreases passing from the Manhattan or Euclidean distance to that of Tchebychev. Additive effects slightly decrease passing from the Tchebychev distance to the Euclidean one. This implies that it is more likely that similarities with SAW decrease, if TOPSIS is endowed with the Tchebychev distance rather than the Euclidean distance. The last effect can be augmented as the number of criteria increases. To appreciate the last insight, one must see how correcting terms a(i) in the proof of Propositions 1 and 3 start to be more distant as the number of criteria grows.

Nevertheless, similarities might change if different normalisation techniques for ratings and trade-off weights are chosen. More broadly, it remains clear the fact that similarities can be observed under different perspectives by DMs and, therefore, similarity results may still be somehow conflicting across different perspectives. In the next Section, we will provide the settings of our experiment where trade-off weights and ratings are randomly generated.

4 Randomised Experiments

In our experimental settings, the set Z of alternatives can change, with the number of alternatives m being equal to 25, 50, 75 or 100; and with the number of criteria n being equal to 3, 6 or 9. Our experiments consist in testing all the possible combinations of alternatives and criteria (for a total of 12 pairs). Each experiment is conducted by endowing TOPSIS with a specific Minkowski distance. Each of the twelve cases is a single experiment. However, the experiment also involves specific choices for ratings and weights before the aggregation processes of SAW and TOPSIS methods. We detail in how we have set randomisation. First, the randomised procedure is articulated into 50 instances, with each providing:

  • criteria weights are randomly generated, being drawn from a uniform probability distribution in [0, 1];

  • criteria are positive;

  • criteria weights are normalised and are the same for TOPSIS and SAW, with the constraint that the sum of the weights across the set of criteria must be equal to 1;

  • ratings are randomly generated, being drawn from a uniform probability distribution in [0, 1];

  • ratings are normalised for TOPSIS methods. We utilise the vector method. Interestingly, Sałabun et al. (2020) state in their conclusions that, for the TOPSIS method, rankings obtained using minmax, max, and vector normalisation method could be quite similar, especially for problems in which a large number of alternatives is considered (this is our case). Moreover, Chakraborty and Yeh (2009) justify the use of the vector normalisation procedure for TOPSIS. The vector method computes the square root of the sum of the squares of valuations for a given criterion. The matrix \((r_{ij})_{m\times n}\) (in STEP2 of TOPSIS methods) is built as follows:

    $$\begin{aligned} r_{ij}=\dfrac{x_{ij}}{\sqrt{\sum _{k=1}^{m} x_{kj}^{2}}}. \end{aligned}$$

  • ratings are not normalised for SAW. It follows that \(r_{ij}=x_{ij}\) for the implementation of the method as described in subsection 3.1.

We utilise the same subsets of criteria weights and ratings as adopted by Zanakis et al. (1998), i.e. the interval [0, 1]. Rankings of SAW and TOPSIS procedures are calculated for each distance in TOPSIS methods. The set of final scores of TOPSIS and SAW do not contain repeated values. The latter implies that ranking produced by the two methods can be seen as bijections from the set of alternatives on integers. Each obtained ranking X can be associated with a bijection \(\sigma :\ Z\ \rightarrow \ X\) where the number of alternatives is m and X is the ranking. Each alternatives has a rank in X. Two distinct alternatives have different ranks.

4.1 Similarity coefficients

In this subsection, we define the measures for quantifying the agreement between recommendation delivered by SAW and TOPSIS methods. Firstly, we refer to the ranking perspective, and discuss six coefficients accounting for rank-order correlation or similarity. Secondly, we focus on three coefficients applicable in the context of choice problems, where the task consists in selecting the best alternative.

4.1.1 Kendall’s coefficient (KE)

Kendall’s coefficient measures the likelihood that alternatives preserve ordering in two different rankings (Kendall, 1948). A pair (a, b) is an ordered couple of two alternatives. A pair (a, b) is concordant if one of the two conditions is true: \(\sigma \left( a \right) > \sigma \left( b \right) \) implies \(\eta \left( a \right) > \eta \left( b \right) \) or \(\sigma \left( b \right) > \sigma \left( a \right) \) implies \(\eta \left( b \right) > \eta \left( a \right) \). Otherwise the pair is discordant. Let us call \(p\) the number of concordant pairs and \(q\) the number of discordant pairs. Kendall’s \(\tau \) is defined as follows:

$$\begin{aligned} \frac{2(p - q)}{m(m-1)}. \end{aligned}$$

No ties in rankings imply that \(\sigma (a)\not =\sigma (b)\) and \(\eta (a)\not =\eta (b)\). Therefore, each pair of alternatives must be concordant or discordant. Since calculations for Kendall coefficient are based on the concordant and discordant pairs, they fail to account directly for the ranks gained by alternatives. However, as noted in (Kadzinski et al., 2013), ranks are of major interest to the DMs when analysing outcomes of decision-making solutions. Therefore, it seems reasonable to additionally account for the rank-oriented measures for quantifying an agreement between different orders (Mukaka, 2012).

4.1.2 Spearman’s coefficient (SPE)

The distance of ranks attained by a specific alternative according to two different methods a is the following: \(\sigma (a) - \eta (a).\) For instance, Spearman’s rank correlation measure is the following:

$$\begin{aligned} 1 - \frac{6}{m(m^{2} - 1)} \sum _{a \in Z}^{}[\sigma (a) - \eta (a)]^{2}. \end{aligned}$$

4.1.3 Weighted Spearman’s coefficient (WSPE)

Weights may be used to take into account distance of ranks in a more significant way. For instance, weighted Spearman’s rank correlation coefficient is the following:

$$\begin{aligned} 1- \frac{6 }{(m^4+m^3-m^2-m)} \sum _{a \in Z}[\sigma (a) - \eta (a)]^{2} \; ( 2m -2 -\sigma (a) - \eta (a) ). \end{aligned}$$

Weights decay when ranks approximate to the bottom of both rankings in the above formulation (Pinto da Costa & Soares, 2005; Genest & Plante, 2003).

4.1.4 Rank Similarity coefficient(RS)

Weights can be asymmetrically utilised for distances of ranks. In other words, weights can be utilised to measure the significance of rank-distances in one single ranking, let’s say \(\sigma \). The last ranking is used as a reference ranking. For instance, rank similarity coefficient incorporates this asymmetric aspect and has recently been presented in Sałabun and Urbaniak (2020) as follows:

$$\begin{aligned} 1- \sum _{a \in Z} \frac{ 2^{-\sigma (a)} }{\max (\mid \sigma (a) -1\mid ,\mid \sigma (a)-m\mid )} \mid \sigma (a) - \eta (a)\mid . \end{aligned}$$

Weights are extremely small for low ranks. In our own symbols, RS1 (RS2) is the rank similarity coefficient with reference method TOPSIS (SAW). By definition, RS1 measures the similarity of rankings of TOPSIS methods against rankings of SAW but not vice versa.

4.1.5 Rank agreement coefficient (RA)

An alternative may achieve the same rank in the recommendations provided by the two methods. More formally, rank agreement coefficient is the following:

$$\begin{aligned} \frac{1}{m} \sum _{a\in Z} \phi (a) \end{aligned}$$

where \(\phi (a)=1\) if \(\sigma (a)=\eta (a)\); otherwise is void. A more general version of this coefficient, that is if ties occur in rankings, is presented in Kadziński and Michalski (2016).

4.1.6 Hit ratio coefficient (HR)

The traditional similarity between recommendations delivered by two scoring procedures has been measured for the first-rank alternative (Barron & Barrett, 1996; Ahn & Park, 2008). Hit ratio coefficient assumes value 1 if two rankings place the same alternative at the first rank; otherwise assumes value 0.Footnote 1 The next two coefficients measure how a first-ranked alternative in one ranking might be dispersed in the second remaining ranking.

4.1.7 Generalised hit ratio coefficient (GHR)

Let \(d^{\sigma }\) be the distance between the first-ranked alternative in \(\sigma \) and the rank obtained by the same alternative in the remaining ranking \(\eta \). Let us call the distance \(d^{\sigma }= \eta (a^{*})-1\) where \(a^{*}\in Z\) such that \(\sigma (a^{*})=1\). Let \(d^{\eta }\) be the same distance if the role of the two rankings is exchanged. Symmetrically, \(d^{\eta }=\sigma (a^{**})-1\) where with \(a^{**}\in Z\) such that \(\eta (a^{**})=1\). Finally, generalised hit ratio coefficient is defined as follows:

$$\begin{aligned} 1- \frac{\max \{ d^{\sigma }, \, d^{\eta } \}}{m-1} \ge 0. \end{aligned}$$

4.1.8 Weak generalised hit ratio coefficient (WGHR)

The next coefficient captures a weaker dispersion of first-ranked alternatives. Weak generalised hit ratio coefficient is the following:

$$\begin{aligned} 1- \frac{\min \{ d^{\sigma }, \, d^{\eta } \}}{m-1} \ge 0. \end{aligned}$$

The closer GHR or WGHR are to 1, the closer first-ranked alternatives.

If some similarity coefficients are correlated, then the simultaneous utilisation of those coefficients might be unnecessary. For instance, SPE correlation, WSPE and KE coefficients are highly correlated and RS1, RS2 coefficients are less correlated to the previous ones (Shekhovtsov, 2021). Nevertheless, we prefer to extend the analysis utilising multiple similarity coefficients, especially in order to increase the robustness of our results.

The pathway of random simulations is the following. Averages of coefficients (except for GHR and WGHR coefficients) over the fifty random instances for each pair of alternatives/criteria are calculated. Regarding GHR and WGHR coefficients, the lowest values over fifty random instances are calculated; this yields a more robust control on first-ranked alternatives’ dispersion. We call similarity indices the averages or the lowest values of similarity coefficients calculated, instance by instance, throughout the rest of the current paper. Similarity indices (as numbers in [0, 1]) are compared across alternatives and criteria as shown in Tables included in the supplementary information.

Across distances used for the TOPSIS, the value function is highly influenced by the number of alternatives. In fact PIS and NIS and, consequently, also the value function can vary considerably as a function of the number of alternatives. It is straightforward to prove that some coordinates of NIS starts decreasing and some coordinates of PIS starts increasing, as alternatives grow in numbers. Therefore, distances of alternatives from NIS and PIS tend to have a high dispersion. Regardless the distance that one adopts in TOPSIS methods, it remains that the aggregate score of an alternative is normalised via the sum of distances of the alternative from NIS and PIS. Therefore, dispersion effects may be mitigated across the three Minkowski distance.

Nevertheless, the next definitions express the fact that an arbitrary similarity index between two MCDM methods might exhibit a monotonic behaviour varying the number of criteria (for a given number of alternatives) or varying the number of alternatives (for a given number of criteria). Assume that there is a family of MCDM problems with \(m_{k}\) alternatives and \(n_{w}\) criteria with \(1\le k \le r, 1 \le w \le s\). Without losing in generality, assume that sequences \(m_{k}, n_{w}\) are increasing. Let \(\phi \) be a similarity index among rankings produced by two MCDM methods for any element of the family of MCDM problems. Similarity index \(\phi \) assumes the following functional form: \(\phi =\phi (m_{k},n_{w})\).

Definition 1

  • A similarity index increases with the number of criteria if \(\phi (m_{k},n_{w}) \le \phi (m_{k},n_{w+1})\), for \(1 \le w < s\), \(k=1,\ldots ,r\).

  • A similarity index \(\phi \) decreases with the number of criteria if \(\phi (m_{k},n_{w}) \ge \phi (m_{k},n_{w+1})\) for \(1 \le w < s\), \(k=1,\ldots ,r\).

  • A similarity index \(\phi \) increases with the number of alternatives if \(\phi (m_{k},n_{w}) \le \phi (m_{k+1},n_{w})\) for \(1 \le k < r\), \(w=1,\ldots , s\).

  • A similarity index \(\phi \) decreases with the number of alternatives if \(\phi (m_{k},n_{w}) \ge \phi (m_{k+1},n_{w})\) for \(1 \le k <r\), \(w=1,\ldots ,s\).

5 Analysis of similarities

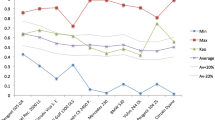
In this section, we discuss and analyse the results of the experiment through the above similarity indices. SAW and TOPSIS methods show higher similarities across the following ranking of distances: (1) Manhattan distance; (2) Euclidean distance; (3) Tchebychev distance. The following evidences are highlighted in Figs. 1, 2, 3, 4, 5, 6, 7, 8  and 9.

Evidence 1

SPE, KE, RA, HR, WSPE, RS1, RS2 indices tend to be higher if TOPSIS is implemented with the Manhattan distance.

Evidence 1 cannot be extended to HR, GHR,WGHR indices (but just for few alternatives/criteria pairs). We focus on the first-ranked alternatives. TOPSIS with the Euclidean distance approximately matches first-ranked alternatives with SAW as many times (or more) as TOPSIS with the Manhattan distance does, if alternatives/criteria pair is (25, 3).

Overall, TOPSIS with Manhattan distance is the procedure that yields rankings closest to the ones of SAW.

RS1 and RS2 indices have an asymmetric way of measuring differences among rankings. From the comparison of RS1 and RS2 indices, it follows that TOPSIS methods are more similar to SAW than the extent to which SAW is close to TOPSIS methods. This asymmetrical result is accurate for each distance. However, this asymmetry tends to vanish for the case of the Manhattan distance. Regarding the results provided in this case, RS1 and RS2 are nearly equal.

The worst case of similarity with SAW is quite evident from our analyses, and discussed in the following Evidence.

Evidence 2

SPE, KE, RS1, RS2, RA, WSPE, GHR indices are the lowest if TOPSIS is endowed with the Tchebychev distance.

Similarity indices are quite close if TOPSIS methods are endowed with Tchebychev and Euclidean distances, when the number of criteria is lower. Moreover, the behaviour of many similarity indices is less predictable if TOPSIS is endowed with the Tchebychev distance. The latter is captured by the following Evidence.

Evidence 3

The range of similarity indices (except RA index) is the highest if TOPSIS is endowed with the Tchebychev distance. The range of RA index is the highest if TOPSIS is endowed with the Manhattan distance.

Fig. 1
figure 1

SPE index

Full size image
Fig. 2
figure 2

KE index

Full size image
Fig. 3
figure 3

RS1 index

Full size image
Fig. 4
figure 4

RS2 index

Full size image
Fig. 5
figure 5

RA index

Full size image
Fig. 6
figure 6

WSPE index

Full size image
Fig. 7
figure 7

HR index

Full size image
Fig. 8
figure 8

GHR index

Full size image
Fig. 9
figure 9

WGHR index

Full size image

We study the monotonic behaviour of similarity indices within our experiment. Specifically, a monotonic behaviour with respect an increase of the number of alternatives (or criteria), especially across the whole ranges of alternatives/criteria, can be highlighted.

Evidence 4

Assume that TOPSIS is endowed with the Euclidean distance. Then, SPE, RS1, WSPE indices increase with the number of alternatives; conversely, RA index decreases with the number of alternatives.

Evidence 5

Assume that TOPSIS is endowed with the Manhattan distance. Then, SPE, RS2, WSPE, GHR, WGHR similarity indices increase with the numbers of alternatives.

TOPSIS with the Manhattan distance shows the above monotonic behaviour in a more robust way. Less evidence of a monotonic behaviour can be found for the Tchebychev distance.

Evidence 6

Assume that TOPSIS is endowed with the Tchebychev distance. Then, RS1 index increases with the number of alternatives. Moreover RA, WSPE, HR indices decrease with the number of alternatives, if the number of criteria is low (that is three criteria).

Summing up, the similarities between TOPSIS (across distances) and SAW tend to be increasing if the number of alternatives grows. A monotonic behaviour with respect an increase of the number of criteria can be highlighted, too.

Evidence 7

Assume that TOPSIS is endowed with the Euclidean distance. Then, SPE, WSPE indices decrease with number of criteria. KE, GHR indices decrease with the number of criteria only for alternatives’ numbers larger or equal than 50.

Evidence 8

Assume that TOPSIS is endowed with the Manhattan distance. Then, RS1, WSPE similarity indices decrease with the number of criteria only for number of alternatives larger or equal than 75. WGHR similarity indices decrease with the number of criteria.

Evidence 9

Assume that TOPSIS is endowed with the Tchebychev distance. Then, SPE, KE, RS1, RS2, WSPE, GHR, WHGR indices decrease with the number of criteria.

Summing up, the similarities between TOPSIS (across distances) and SAW tend to be decreasing if the number of criteria grows. As we expect from the analysis of formal properties of the methods, TOPSIS with the Tchebychev distance shows a more robust monotonic behaviour.

6 A note on rank reversals in TOPSIS methods

A supporting evidence of the discussed similarity results can be viewed through the lens of the rank reversal phenomenon. TOPSIS methods suffer from rank reversals, while SAW does not. It may be reasonable that TOPSIS with the Manhattan distance (being the closest to SAW) might be less affected from the rank reversal phenomenon. As such, we provide an example that takes into account the previous similarity analyses. In fact, the pair (25, 9) of alternatives/criteria is one of the worst-performing across many similarity measures. As such, a random instance is provided for this pair. The ranking, produced by TOPSIS with the Manhattan distance, is then calculated. Then, one alternative is added to this random instance, bringing the number of alternatives to 26, while the the number of criteria remains unchanged; a new ranking, obtained with the Manhattan distance, is then calculated. The two obtained rankings are reported in Table 2: no rank reversal occurs.

TOPSIS with Manhattan distance inherits a nice property of SAW, i.e., the lack of rank reversals, in this random instance. One might object that the outcome of this experiment may depend on the large number of alternatives. As such, we show a similar example, with the only difference of the use of the Tchebychev distance in TOPSIS. The obtained rankings are reported in Table 3: many rank reversals appear.

Ceteris paribus the number of alternatives (and criteria), TOPSIS with the Manhattan distance might produce less rank reversals. Therefore, the lack of rank reversals in Table 2 does not only depend on a large number of alternatives. It remains that the analysis on rank reversals across distances in TOPSIS methods should be more robust and accurate.

Table 2 The first column represents the ranking of TOPSIS with the Manhattan distance for 25 alternatives. The second column represents the ranking of TOPSIS with the Manhattan distance for 26 alternatives
Full size table
Table 3 The first column represents the ranking of TOPSIS with the Tchebychev distance for 25 alternatives. The second column represents the ranking of TOPSIS with the Tchebychev distance for 26 alternatives
Full size table

7 Conclusions

In this study, some formal properties for MCDM methods have been studied in TOPSIS approaches endowed with Euclidean, Manhattan and Tchebychev distances. These properties describe the degree of the additivity of the value function and the sensitivity to trade-off weights. We analyse howmuch formal properties satisfied by TOPSIS methods are close to the ones satisfied by SAW. In regard to those methodological insights, we conduct simulated experiments in order to select the procedure of TOPSIS which returns the closest results to SAW, which can be regarded as the simplest possible aggregation method. Experiments are is conducted through randomly uniform valuations in decision matrices in order to produce unbiased rankings via TOPSIS methods.

The adoption of the Manhattan distance in TOPSIS methods yields recommended rankings which are extremely close to the ones of SAW. TOPSIS with the Manhattan distance is the procedure closer to the SAW method against many DMs’ preferences: variation in ranks, preservation of ranks, weighted variations in ranks, first-ranked alternatives. Moreover, under asimmetric similarity measures, TOPSIS methods are similar to SAW more than the extent to which SAW method is similar to TOPSIS methods. As a reasonable consequence of the previous result, we also show how TOPSIS is less prone to the phenomenon of rank reversals in its generated rankings, if the Manhattan distance is implemented in TOPSIS methods.

Similarities between TOPSIS and SAW approaches may vary across the range of alternatives and criteria chosen for our experimental study. Increased similarity indices tend to occur when the number of alternatives grows, especially if TOPSIS is endowed with the Manhattan distance. Conversely, there is a large number of scenarios for which the pattern shown by similarity indices is decreasing across variations in the number of criteria, especially if TOPSIS is endowed with the Tchebychev distance. Our conclusions support the literature dealing with the monotonic behaviour of similarities between TOPSIS and SAW. In fact, similar results have been found if the number of criteria is comparable or larger than the number of alternatives (Zanakis et al., 1998) (Zamani-Sabzi et al., 2016). However, the above monotonic results are less evident if DMs measure the dispersion of first-ranked alternatives.

It would be useful to compare rankings produced by different aggregation methods to the ones of SAW, especially if criteria weights have an asymmetrical relevance or ratings are biased. Furthermore, some attention could be devoted to the analysis of relevant cases based on specific endogenous characteristics of the instances which are considered (as done by Çelikbilek and Tüysüz (2020)), in order to further assess the performance of the studied approaches against some special distribution of performance data. Lastly, the importance of distances in TOPSIS methods have on the phenomenon of rank reversal deserves a more complete analysis.