1 Introduction

Given n items (in multi-attribute decision making, typically criteria, alternatives, voting powers of decision makers, subjective probabilities, levels of performance with respect to a fixed criterion etc.), the structure of pairwise comparisons is often represented by graphs (Gass, 1998). The minimally sufficient number of comparisons in order to have a connected system of preferences is \(n-1\), and the pairs of items compared can be associated to the edges of a spanning tree on n nodes. This system has no redundance at all, and the calculated weight vector is highly sensitive to the change of any comparison. Observe that the average degree in a spanning tree is \((2n-2)/n = 2 -2/n\), i.e., every item is compared to (almost) 2 other items in average. We would like to keep the number of comparisons low, namely around the average degree 3 or a bit more, and compare the weight vectors calculated from several such graphs to determine the best filling in pattern that provides the closest weights to the ones computed from the complete matrix.

In our research predetermined graphs are used, thus we assume that the set of comparisons can be chosen, and the whole questionnaire should be prepared a priori.

Some of the examined models also use additional ordinal information, thus the evaluation of this information is a main contribution of our study as well.

Our aim is to gain as much information from the decision maker’s revealed preferences as possible. We would like to find out if there is better ordinal information than the one usually used by multi-attribute decision making models, and whether we can find better solutions even without additional ordinal information. The paper deals with specified numbers of comparisons, however, the key question remains valid for all incomplete pairwise comparison matrices.

The remainder of this paper is organized as follows. Sect. 2 provides a brief summary of the related literature and research gaps. The used methodology is detailed in Sect. 3, where besides the method of pairwise comparisons, as well as the relevant graph theoretical concepts (Sect. 3.1), the applied simulation process to compare the different models is also included (Sect. 3.2). The analyzed models and the associated filling in patterns are presented in Sect. 4, while Sect. 5 shows the obtained results. Finally, Sect. 6 concludes and raises some further research questions.

2 Literature review

The main goal of multi-attribute decision making (MADM) is to determine the best or the best few, perhaps the complete ranking of the discrete number of alternatives based on a finite number of (usually conflicting) qualitative and/or quantitative criteria (Triantaphyllou, 2000).

It is not uncommon that the MADM models use some part of the ordinal information of the ranking of items from the decision maker at the beginning of the process as well, namely the best, the worst or both alternatives. The most popular such methodologies are the SMART (simple multi-attribute rating technique) (Edwards, 1977), the Swing method (von Winterfeldt and Edwards, 1986), the SMARTS (SMART using Swings) and the SMARTER (SMART Exploiting Ranks) (Edwards and Barron, 1994; Mustajoki et al., 2005), and last but not least the best-worst method (Rezaei, 2015). The latter one generated an indeed large literature in the last few years (Mi et al., 2019), with theoretical extensions and studies (Liang et al., 2020; Mohammadi and Rezaei, 2020) as well as real applications (Rezaei et al., 2016). However, the significance of the ordinal information used by these models has barely been studied.

One of the most fundamental concepts of MADM is the method of the pairwise comparisons (Thurstone, 1927). It is also the cornerstone of the indeed popular and widely used methodology of the Analytic Hierarchy Process (AHP) (Saaty, 1977), where these comparisons form a pairwise comparison matrix (PCM).

The incomplete case of PCMs was originally proposed by (Harker, 1987) to reduce the number of questions in the AHP, especially in group decision making. Since that besides their application for different problems (Bozóki et al., 2016), many aspects of incomplete PCMs has been examined in detail from the inconsistency measures (Szybowski et al., 2020) and their thresholds (Ágoston and Csató, 2022) to different optimal completions (Fedrizzi and Giove, 2007; Zhou et al., 2018). As answering all the questions is time-consuming, there were several proposals to solve this problem (Triantaphyllou, 2000). Based on Revilla and Ochoa (2017) if we ask the respondents, they clearly prefer shorter (with a maximum length of 20 minutes) questionnaires and surveys, while longer questionnaires result in lower data quality as well (Deutskens et al., 2004). These time spans more or less correspond to the number of questions included in our models. We focus on a similar problem as the reduction of comparisons, however, we assume that the whole questionnaire has to be prepared before the decision making process and we cannot ask the decision makers to modify some answers, thus our approach is in some sense similar to Amenta et al. (2021). There are only a few studies dealing with the question that which pattern of comparisons should we use in a given problem (Szádoczki et al., 2022), and to our knowledge, none of them regards additional ordinal information as well, thus in this paper we would like to eliminate this research gap. The comparison of different priority vectors has an important role in our study, which has been also used in the different optimizations of aggregation of group preferences (Duleba et al., 2021) and in several weight calculation problems (Kou and Lin, 2014).

3 Methodology

3.1 Pairwise comparisons and their graph representation

The pairwise comparison matrix technique can be applied in decision problems both to determine the weights of the different criteria and to evaluate the alternatives according to a criterion.

Definition (Pairwise comparison matrix (PCM)) Let us denote the number of criteria (alternatives) in a decision problem by n. The \(n\times n\) matrix \(A=[a_{ij}]\) is called a pairwise comparison matrix, if it is positive (\(a_{ij}>0\) for \(\forall \) i and j) and reciprocal (\(1/a_{ij} = a_{ji}\) for \(\forall \) i and j).

The general element of a PCM \(a_{ij}\) shows how many times item i is better/larger/stronger/ more important than item j.

There are several techniques to calculate a weight vector from a PCM that shows the importance of compared items. Probably the two most commonly used methods are the logarithmic least squares (LLSM) (Crawford and Williams, 1985) and the eigenvector (Saaty, 1977) techniques, given by the following formulas respectively:

$$\begin{aligned}&\sum _{i=1}^n\sum _{j=1}^n \left( \ln (a_{ij})-\ln \left( \frac{w_i}{w_j}\right) \right) ^2\rightarrow \min \end{aligned}$$
(1)
$$\begin{aligned}&A\cdot w=\lambda _{\max }\cdot w \end{aligned}$$
(2)

Where w denotes the weight vector with the general element \(w_i\), A is an \(n\times n\) PCM and \(\lambda _{\max }\) is the maximal eigenvalue of A. As we are studying graphs in our research, we should also mention that the combinatorial weight calculation method (Tsyganok, 2000), which is based on the weight vectors gained from different spanning trees provides the same solution as the LLSM if we use the geometric mean (Lundy et al., 2017). The comparison of this method with other weight calculation techniques can be found in Tsyganok (2010).

Another important aspect of PCMs is their inconsistency.

Definition (Consistent PCM) A PCM is said to be consistent if and only if \(a_{ik}=a_{ij}a_{jk} \forall i,j,k\). If a PCM is not consistent, then it is called inconsistent.

Of course, there are different levels of inconsistency and several inconsistency indices have been proposed to measure this problem (Brunelli et al., 2013), which satisfy different properties (Brunelli, 2017). However, the most popular one is probably still the Consistency Ratio (CR) (Saaty, 1977). In order to define the CR, we need the Consistency Index (CI), which is given as

$$\begin{aligned} CI=\frac{\lambda _{\max }-n}{n-1} \end{aligned}$$
(3)

Where \(\lambda _{\max }\) is the largest eigenvalue of the PCM. The Consistency Ratio can be calculated as

$$\begin{aligned} CR=\frac{CI}{RI} \end{aligned}$$
(4)

Where RI is the Random Index, which is the average CI obtained from a large enough set of randomly generated matrices of size n.

In case of incomplete data, namely when some elements of the PCM are missing, we are talking about an incomplete PCM. The absence of these elements can be caused by several different reasons: the loss of data, some comparisons are simply not possible (Bozóki et al., 2016) or the decision maker does not have time, possibility or willingness to fill in all the \(n(n-1)/2\) comparisons (it is sufficient to focus only on the elements above the principal diagonal of the matrix because of the reciprocity).

In our research the most important case is the latter one, as we examine different kinds of filling in patterns of incomplete PCMs, thus we assume that the set of pairwise comparisons to be made can be chosen.

The weight calculation techniques can be extended to the incomplete case, but the results depend on both the number of known comparisons and their positioning. We assume that it is possible to find a pattern of pairwise comparisons, that minimizes experts’ efforts and accumulated estimation errors, while ensuring estimation stability. In order to compare the effect of different arrangements of known elements (filling in patterns), we use the graph representation of the PCM (Gass, 1998). The representing graph is an undirected graph, where the vertices denote the criteria/alternatives, and there is an edge between any two vertices if and only if the comparison has been made for the two respective items (the associated element of the PCM is known).

There are several different attributes that are studied in connection with decision making problems, among which regularity of comparisons (in some sense) is, indeed, an important one (Kulakowski et al., 2019; Wang and Takahashi, 1998). If we use the graph representation of the PCM, the most common definition of regularity that we use in this paper, can be seen below.

Definition (\({\varvec{k}}\)-regularity) A graph is called k-regular if every vertex has k neighbours, which means that the degree of every vertex is k.

In decision problems regularity ensures a certain level of symmetry, it means that every item is compared to the same number of elements. This kind of property is also required in the design of some sport tournaments (Csató, 2017).

As k-regularity is not possible, when both the number of vertices (n) and the level of regularity (k) are odd, Szádoczki et al. (2022) defined the graphs that are the closest to k-regularity in this case, as follows.

Definition (\({\varvec{k}}\) -quasi-regularity) A graph is called k-quasi-regular if exactly one vertex has degree \(k+1\), and all the other vertices have degree k.

In case of indirect relations, when there is no direct comparison between two elements, the small errors of the intermediate comparisons can add up (Szádoczki et al., 2020). The diameter of the representing graph can measure this problem indeed naturally.

Definition (Diameter of a graph) The d diameter of a graph G is the length of the longest shortest path between any two vertices:

$$\begin{aligned} d=\max _{u,v \in V(G)}\ell (u,v), \end{aligned}$$
(5)

where V(G) denotes the set of vertices of G and \(\ell (.,.)\) is the graph distance between two vertices, namely the length of the shortest path between them (in our case the length of every edge is one).

The diameter also seems to be a crucial property in case of the weight calculation method based on spanning trees (Kadenko and Tsyganok, 2020).

It is important to note that the solution of the weight calculation problem is unique in case of incomplete PCMs if and only if the representing graph is connected, thus there are at least indirect comparisons between the pairs of items (Bozóki et al., 2010).

Definition (Connected graph) In an undirected graph, two vertices u and v are called connected if the graph contains a path from u to v. A graph is said to be connected if every pair of vertices in the graph is connected.

It is worth to examine some of the so-called stronger kind of connectedness measurements as well regarding the representing graph of a PCM. From these indicators the following property has special importance in our study.

Definition (\({\varvec{k}}\) -edge-connectivity) A graph G is called k-edge-connected if it remains connected whenever fewer than k edges are removed from G. Formally: let \(G=(V,E)\) be an undirected graph, where V is the vertex set, while E is the edge set of G. If \(G^{\prime }=\left( V,E\setminus H\right) \) is connected for \(\forall H\subseteq E\), where \(\left| H\right| <k\), then G is k-edge-connected. The edge connectivity of G is the maximum value k such that G is k-edge-connected.

3.2 The simulation process

We apply extended numerical experiments to compare different filling in models of pairwise comparisons. In our simulations, the weight vectors are calculated using the natural extension of the two most popular weighting techniques, the eigenvector method and LLSM, to the incomplete PCM case. The former one is based on the CR-minimal completion (CREV), and its principal right eigenvector (Bozóki et al., 2010, Sects. 3 and 5). The LLSM’s optimization problem includes the known elements of the matrix, the optimal solution can be calculated by solving a system of linear equations (Bozóki et al., 2010, Sects. 4), furthermore, it can also be written as the geometric mean of weight vectors calculated from all spanning trees (Bozóki and Tsyganok, 2019). As we mentioned, in both of the CREV and the LLSM models the optimal solution is unique if and only if the graph of comparisons is connected. We compare the weight vectors obtained based on different filling in models to the ones calculated from the complete PCMs. As for the measurements of comparison, we use three types of metrics:

  • distances, as the most commonly used cardinal measures, which are represented by the Euclidean distance (\(d_{euc}\)), the Chebyshev distance (\(d_{cheb}\)), and the Manhattan distance (\(d_{man}\)),

  • rank correlation coefficients, as the basic ordinal indicators, namely the Kendall rank correlation (Kendall’s \(\tau \)), and the Spearman rank correlation coefficient (Spearman’s \(\rho \)),

  • and last but not least, the so called compatibility (or similarity) indices, which are argued in the literature to be the most important measures to compare priority vectors (Garuti, 2017). In our analysis we include Garuti’s compatibility index (G index) (Garuti, 2020), the cosine similarity index (C index) (Kou et al., 2021), and the dice similarity index (D index) (Ye, 2012).

The above-mentioned indicators are given by the following formulas, respectively:

$$\begin{aligned}&d_{euc}(u,v)=\sqrt{\sum _{i=1}^{n}(u_i-v_i)^2} \end{aligned}$$
(6)
$$\begin{aligned}&d_{cheb}(u,v)=\max _{i\in 1, \ldots , n} {|u_i-v_i|}\end{aligned}$$
(7)
$$\begin{aligned}&d_{man}(u,v)=\sum _{i=1}^{n} |u_i-v_i|\end{aligned}$$
(8)
$$\begin{aligned}&\tau (u,v)=\frac{n_c(u,v)-n_d(u,v)}{n(n-1)/2} \end{aligned}$$
(9)
$$\begin{aligned}&\rho (u,v)=1-\frac{6\sum _{i=1}^{n}R(u_i)-R(v_i)}{n(n^2-1)} \end{aligned}$$
(10)
$$\begin{aligned}&G(u,v)=\frac{1}{2}\sum _{i=1}^{n}\left( \frac{\min (u_i,v_i)}{\max (u_i,v_i)}(u_i+v_i)\right) \end{aligned}$$
(11)
$$\begin{aligned}&C(u,v)=\frac{\sum _{i=1}^{n}u_iv_i}{\sqrt{\sum _{i=1}^{n}(u_i)^2}\sqrt{\sum _{i=1}^{n}(v_i)^2}}\end{aligned}$$
(12)
$$\begin{aligned}&D(u,v)=\frac{2\sum _{i=1}^{n}u_iv_i}{\sum _{i=1}^{n}(u_i)^2+\sum _{i=1}^{n}(v_i)^2} \end{aligned}$$
(13)

where u denotes the weight vector gained from a certain filling in pattern and v is the weight vector calculated from the complete matrix. u and v are normalized by \( \sum _{i=1}^{n} u_i = 1\) and \( \sum _{i=1}^{n} v_i = 1,\) respectively, and \(v_i\) and \(u_i\) denote the ith element of the appropriate vectors. \(n_c(u,v)\) denotes the number of concordant pairs and \(n_d(u,v)\) the number of discordant pairs of the examined vectors, while R(.) shows the rank of the given element within the appropriate vector. The range of the Kendall’s \(\tau \) and Spearman’s \(\rho \) is \([-1,1]\), and considering the notation above, the higher value indicates a better performance of the given filling in pattern. In case of the compatibility indices (G, C, and D) the range corresponds to [0, 1], and similarly, the higher value is the better. On the other hand, here the distances can be interpreted as errors, thus their smaller level is preferred. This way we use the most commonly applied categories of closeness measures in case of priority vectors, and also include several of them to see if the results depend on the given category or may even on the specific metric.

Our simulations are in a sense similar to the ones in Szádoczki et al. (2022), but (besides using other filling patterns and other metrics) we apply elementwise perturbations instead of their matrixwise solution, and the handling of scales is improved in our case.

The process of the simulation for a given n consisted of the following steps:

  1. 1.

    We generated n random weights (the general weight is denoted by \(w_i\)), where \(w_i \in [1,9]\) is a uniformly distributed random real number for \(\forall i \in 1, 2, \ldots , n\). We calculated random \( n \times n\) complete and consistent PCMs, where the elements of the matrices were given as follows:

    $$\begin{aligned} a_{ij}=w_i/w_j \end{aligned}$$
    (14)
  2. 2.

    Then we used three different special perturbations of the elements of the consistent matrices to get inconsistent PCMs with three well-distinguishable inconsistency levels. We denote these levels by weak, modest and strong given with the following formulas:

    $$\begin{aligned}&{\hat{a}}^{weak}_{ij}={\left\{ \begin{array}{ll} a_{ij}+\varDelta _{ij} &{} :a_{ij}+\varDelta _{ij}\ge 1\\ \frac{1}{1-\varDelta _{ij}-(a_{ij}-1)}&{} :a_{ij}+\varDelta _{ij}< 1 \end{array}\right. } \varDelta _{ij} \in [-1,1] \end{aligned}$$
    (15)
    $$\begin{aligned}&{\hat{a}}^{modest}_{ij}={\left\{ \begin{array}{ll} a_{ij}+\varDelta _{ij} &{} :a_{ij}+\varDelta _{ij}\ge 1\\ \frac{1}{1-\varDelta _{ij}-(a_{ij}-1)}&{} :a_{ij}+\varDelta _{ij}< 1 \end{array}\right. } \varDelta _{ij} \in \left[ -\frac{3}{2},\frac{3}{2}\right] \end{aligned}$$
    (16)
    $$\begin{aligned}&{\hat{a}}^{strong}_{ij}={\left\{ \begin{array}{ll} a_{ij}+\varDelta _{ij} &{} :a_{ij}+\varDelta _{ij}\ge 1\\ \frac{1}{1-\varDelta _{ij}-(a_{ij}-1)}&{} :a_{ij}+\varDelta _{ij}< 1 \end{array}\right. } \varDelta _{ij} \in [-2,2] \end{aligned}$$
    (17)

    Where \({\hat{a}}^{weak}_{ij}\), \({\hat{a}}^{modest}_{ij}\) and \({\hat{a}}^{strong}_{ij}\) are the elements of the perturbed matrices, \(a_{ij}\) is the element of the consistent matrix, \(a_{ij}\ge 1\) (thus we only perturb the elements above one and keep the reciprocity of the matrices), and \(\varDelta _{ij}\) is uniformly distributed in the given ranges. This perturbation is able to provide ordinal differences as well (when \({\hat{a}}_{ij}<1\)). However, we account for the contrast that can be examined above and below 1, thus our perturbed data is uniformly distributed around the original element on the scale presented by Fig. 1. Our perturbation method aims to ensure 3 different and meaningful inconsistency levels and it is, indeed, correlated with the Consistency Ratio (CR), as it is shown in Fig. 2. We tested several combinations of parameters, and found that they resulted in the most relevant levels of CR.

  3. 3.

    We deleted the respective elements of the matrices in order to get the filling in pattern that we were examining, and applied the LLSM and the CREV techniques to get the weights. In case of the models that use ordinal information, we always chose the needed element according to the examined weight calculation method, based on the complete, perturbed PCM (thus we assume that the decision maker can provide accurate ordinal data). The certain models’ distances, rank correlations and compatibility indices were computed with respect to the weights that were calculated from the complete inconsistent matrices. The compared filling in patterns were the ones presented in great detail in Sect. 4, which are represented by the following graphs:

    1. (i)

      Best-worst graph

    2. (ii)

      TOP2 graph

    3. (iii)

      Best-random graph

    4. (iv)

      Random-random graph

    5. (v)

      3-(quasi-)regular graph with minimal diameter

    6. (vi)

      Union of two random edge-disjoint spanning trees

    7. (vii)

      Random 2-edge-connected graph

  4. 4.

    We repeated steps 1-3 for 10000 times for every level of inconsistency (thus altogether we examined 30000 PCMs for a given n). Finally, we saved the mean of the applied metrics for the different weight calculation methods and filling in patterns.

Fig. 1
figure 1

The ratio scale \(1/9, \ldots , 9\) and the perturbation of elements

Full size image
Fig. 2
figure 2

The relation between CR and our element-wise perturbation. Each point shows the average CR of 1000 randomly generated perturbed PCMs

Full size image

In case of (vi) and (vii) we randomly generated 10000 graphs satisfying the required properties and used them in the simulations. As for (v), when there were more graphs, which met the requirements, we randomly chose one of them at every iteration.

It is worth to include a small theoretical analysis of the simulations to see how they work in general.

Remark

The distribution of the elements of PCMs in the simulation is independent of n. This property holds for both consistent and perturbed PCM cases.

The reason behind this is as follows. If we analyze our simulation process, we can see that at first the elements of a given matrix are generated independently from n, and then they are placed into the \(n\times n\) PCM. The histograms of the matrix elements above 1 in the different perturbation cases, based on large samples containing 1 million elements each are presented in Fig. 3.

Fig. 3
figure 3

The histograms of the \(\ge 1\) elements of PCMs in case of different perturbations based on a sample of 1 million elements

Full size image

It can be seen that the higher the level of perturbation (inconsistency), the higher the chance to have large (extreme) matrix elements.

It also makes sense to consider the average of the maximal elements of the analyzed PCMs and the average number of ordinal perturbations (when the ordinal preference between two items is changed due to perturbation). These details are presented in Tables 1 and 2, respectively, for our specific simulations.

Table 1 The summary of the mean of largest elements in the PCMs based on the simulations
Full size table
Table 2 The average number of ordinal perturbations in the simulations
Full size table

As one can see, the higher the number of alternatives (criteria), the higher the average maximal element in the matrices. However, this is the case only because in a larger matrix we have a larger sample of elements, thus the maximum has a higher probability to be an extreme element. Naturally, the stronger perturbation also results in larger maximal element (as it is also suggested by the histograms). As for the ordinal perturbations, we can see that the average number of them for all n in case of the weak perturbation level is slightly below 20% (\(\approx \)19%) of the possible comparisons, while it is slightly above 25% (\(\approx \)27%) for the strong level.

4 Filling in patterns

As we mentioned earlier, we would like to keep the number of comparisons low in the analyzed models, the average degree of the representing graphs should be approximately 3. All in all we chose to examine seven different filling in patterns, from which the first three use additional ordinal information of the ranking as well. These models (and their associated graphs) are as follows.

  1. (i)

    Best-worst graph

  2. (ii)

    TOP2 graph

  3. (iii)

    Best-random graph

  4. (iv)

    Random-random graph

  5. (v)

    3-(quasi-)regular graph with minimal diameter

  6. (vi)

    Union of two random edge-disjoint spanning trees

  7. (vii)

    Random 2-edge-connected graph

The detailed description of these models can be found below.

(i) Best-worst graph The name of the model comes from the popular best-worst method (Rezaei, 2015), where only the best and the worst items are compared to all the others. We use exactly this filling in pattern, where only two rows and columns are completed (the ones associated with the best and the worst items), and the related graph is the union of two star graphs, which results in \(2n-3\) comparisons. We examine this case, because it is widely used and fits perfectly within the outline of our paper. It is important to note that this model utilizes some additional ordinal information, however, we also examine the same graph representation with other ordinal data, namely when not the best and the worst elements are the highlighted ones.

(ii) TOP2 graph Intuitively in general, the more comparisons are made in connection with one particular item, the more accurate our estimation of its weight becomes. In most of the cases the first few places of the ranking are much more important for the decision maker, than the last few. The TOP2 model (Juhász, 2021) suggests to compare all the items only to the best and the second best elements. One could argue that in the best-worst case, it is easier for the decision maker to choose the best and the worst elements compared to the best and the second best ones. However, if we assume that it is always possible for the decision maker to find the best and the worst elements, then we can remove those as the first step and find the new best and worst items, thus we can determine the best and the second best as well. The advantages of the models that use ordinal information are emphasized in the multicriteria nature of the problems (Rezaei, 2015). The associated graph of this pattern is the aforementioned union of two star graphs, of course with different highlighted vertices than before.

(iii) Best-random graph It also makes sense to investigate, whether it is really necessary to ask the decision maker to provide additional ordinal information, beside just naming the best item. Thus, we consider the Best-random model, in which the elements are compared only to the best one and a randomly chosen other item. The associated graph is still the union of two star graphs, however in this case we use less ordinal information.

(iv) Random-random graph As a benchmark for the previous models, we also examine the case, when no additional ordinal information is included, and the two highlighted vertices are both chosen randomly. This is the last case, when the associated graph is the union of two star graphs, for which an example on 6 nodes is shown in Fig. 4.

Fig. 4
figure 4

The union of two star graphs on \(n=6\) vertices, which is the associated graph of the (i) Best-worst, (ii) TOP2, (iii) Best-random, and (iv) Random-random models. Here the highlighted vertices are 2 and 5

Full size image

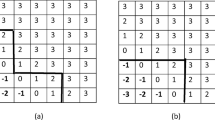
(v) 3-(quasi-)regular graph with minimal diameter This filling in pattern was suggested by Szádoczki et al. (2022). No additional ordinal information is needed, and the cardinality of the model fits into the examined cases. The (quasi-)regularity results in some kind of symmetry, while the minimal diameter ensures that the comparisons are close enough to the direct ones (the shortest path between any two vertices is not so long). The number of comparisons for these graphs is 3n/2 in case of even number of vertices (regularity) and \(3n/2+1/2\) in case of odd number of vertices (quasi-regularity). Two examples on \(n=5\) and \(n=6\) vertices can be seen in Fig. 5.

Fig. 5
figure 5

Two examples for 3-(quasi-)regular graphs with minimal diameters (\(d=2\)). The left one is the only 3-quasi-regular graph with minimal diameter on \(n=5\) vertices, while the right one is one of the two 3-regular graphs with minimal diameter on \(n=6\) vertices

Full size image

(vi) Union of two random edge-disjoint spanning trees Graph based decision making has a special interest in spanning trees as they are the minimal units from which we can calculate weight vectors. The star graph is a special spanning tree as well, thus the union of two random spanning trees of a graph can be seen as a generalization of the union of two star graphs. For the sake of simplicity the model examines only random edge-disjoint spanning trees. This way the gained union contains \(2n-2\) edges (comparisons). An example of two edge-disjoint spanning trees on \(n=5\) vertices can be seen in Fig. 6.

Fig. 6
figure 6

Two edge-disjoint spanning trees on \(n=5\) vertices, which, when unified, form the 3-quasi-regular graph with minimal diameter on 5 vertices that can be seen in Fig. 5

Full size image

(vii) Random 2-edge-connected graph 2-edge-connected graphs remain connected if we remove any one of their edges. As the union of two star graphs satisfies this property, this can be considered (according to the number of graphs) an even more common generalization of the union of two star graphs based on this connectedness measurement. As there are many 2-edge-connected graphs with different cardinalities, the model contains only the graphs with \(2n-3\) or \(2n-2\) edges. An example that does not fit into any of the previously listed filling in patterns, a 2-edge-connected graph with \(2n-3\) edges, is presented in Fig. 7.

Fig. 7
figure 7

A 2-edge-connected graph on \(n=6\) vertices with \(2n-3\) edges that does not satisfy the properties of any other examined model

Full size image

The numbers of possible non-isomorphic graphs for the different filling in patterns are presented in Table 3.

Table 3 The number of non-isomorphic graphs for the different cases
Full size table

As one can see the number of graphs for the union of two edge-disjoint spanning trees (vi) and the 2-edge-connected case with \(2n-3\) or \(2n-2\) edges (vii) are, in a way, outliers from this point of view. In order to count the number of those graphs, we used Wolfram Mathematica (Wolfram Research, 2021), nauty and Traces (McKay and Piperno, 2014), and IGraph/M (Horvát, 2020). The union of two star graphs (i-ii-iii-iv) is on the other end of the spectrum, where there is only one non-isomorphic graph for every n.

The discussed filling in patterns and the associated numbers of comparisons are summarized in Table 4.

Table 4 The summary of the cardinality of the graphs’ edges (the number of comparisons)
Full size table

The cardinality of the different graphs, namely the required number of comparisons is, indeed, similar. The inclusion of models, which utilize additional ordinal data (i-ii-iii), makes it possible to evaluate this information as well, which is an important contribution of our paper.

5 Simulation results

The results of the simulations are presented in four types of figures (all of them are sorted by n):

  1. 1.

    Figures 8, 9, 10, 11, 12 and 13 show the Euclidean distances (y axis) and Kendall’s taus (x axis),

  2. 2.

    Figures 14, 15, 16, 17, 18 and 19 show the cosine similarity indices (y axis) and Garuti’s compatibility indices (x axis),

  3. 3.

    Figs. A1, A2, A3, A4, A5 and A6 show the Chebyshev distances (y axis) and Spearman’s rhos (x axis),

  4. 4.

    finally, Figs. A7, A8, A9, A10, A11 and A12 show the Manhattan distances (y axis) and dice similarity indices (x axis) for the different models in case of the given perturbation level and the given weight calculation technique.

It is important to note that for the distances the smaller value, and in case of the rank correlation coefficients and compatibility indices the higher level indicates the better performance. Thus for the first, third and fourth types of figures (Figs. 8, 9, 10, 11, 12, 13, A1, A2, A3, A4, A5, A6, A7, A8, A9, A10, A11 and A12) models closer to the bottom right corner are the preferred ones. In case of the second type of figures (Figs. 14, 15, 16, 17, 18 and 19) the upper right corner provides the best results. The third and fourth types of figures can be found in the online Appendix A, mainly because we found that the metrics coming from the same category (distances, rank correlations, compatibility indices) tend to provide similar results. Now, let us analyze the results of the first type of figures in more detail.

Fig. 8
figure 8

The results of the simulation for \(n=5\). The following notations are used: \(d_{euc}\)–Euclidean distance, Kendall’s \(\tau \)–Kendall rank correlation coefficient, ‘Weak’, ‘Modest’ and ‘Strong’ refers to the level of perturbation. Every subfigure shows the mean computed from 10000 pairwise comparison matrices

Full size image
Fig. 9
figure 9

The results of the simulation for \(n=6\). The following notations are used: \(d_{euc}\)–Euclidean distance, Kendall’s \(\tau \)–Kendall rank correlation coefficient, ‘Weak’, ‘Modest’ and ‘Strong’ refers to the level of perturbation. Every subfigure shows the mean computed from 10000 pairwise comparison matrices

Full size image
Fig. 10
figure 10

The results of the simulation for \(n=7\). The following notations are used: \(d_{euc}\)–Euclidean distance, Kendall’s \(\tau \)–Kendall rank correlation coefficient, ‘Weak’, ‘Modest’ and ‘Strong’ refers to the level of perturbation. Every subfigure shows the mean computed from 10000 pairwise comparison matrices

Full size image
Fig. 11
figure 11

The results of the simulation for \(n=8\). The following notations are used: \(d_{euc}\)–Euclidean distance, Kendall’s \(\tau \)–Kendall rank correlation coefficient, ‘Weak’, ‘Modest’ and ‘Strong’ refers to the level of perturbation. Every subfigure shows the mean computed from 10000 pairwise comparison matrices

Full size image
Fig. 12
figure 12

The results of the simulation for \(n=9\). The following notations are used: \(d_{euc}\)–Euclidean distance, Kendall’s \(\tau \)–Kendall rank correlation coefficient, ‘Weak’, ‘Modest’ and ‘Strong’ refers to the level of perturbation. Every subfigure shows the mean computed from 10000 pairwise comparison matrices

Full size image
Fig. 13
figure 13

The results of the simulation for \(n=10\). The following notations are used: \(d_{euc}\)–Euclidean distance, Kendall’s \(\tau \)–Kendall rank correlation coefficient, ‘Weak’, ‘Modest’ and ‘Strong’ refers to the level of perturbation. Every subfigure shows the mean computed from 10000 pairwise comparison matrices

Full size image

Naturally, the outcomes suggest that the higher level of perturbation, namely the higher inconsistency leads to higher distances and lower rank correlation coefficients.

Despite of the used additional ordinal information the (i) Best-worst and (iii) Best-random filling patterns were performing according to both the distance and rank correlation measurements more or less the same as the (iv) Random-random case, which is based on an identical graph without any further information. This would suggest that the additional ordinal information does not provide significant improvement.

The outcomes for the (ii) TOP2 model are much better regarding both of our distance and rank correlation indicators, and it convincingly outperformed the union of two star graphs with other centers (i-iii-iv). However, surprisingly enough, the (vi) Union of two random edge-disjoint spanning trees provided the best weight vectors, basically, in every case according to all distances and rank correlations, without any additional ordinal information. Thus, according to our simulations, this filling in pattern results in weight vectors and rankings, closest to the ones, computed from the complete PCMs for all the used weight calculation methods and inconsistency levels. It is important to note that this filling in pattern usually contains one more edge than most other patterns, however, the results are still quite convincing.

As for the (v) 3-quasi-regular graphs with minimal diameter, it performs well in case of smaller problems, but starts to decline as n grows. However, it still outperforms most of the models that use additional information. It is also true that for larger number of vertices this case uses the smallest number of edges (comparisons), which can also contribute to the aforementioned trend.

The (vii) Random 2-edge-connected graph always performs worse than (vi), but better, than (i), (iii) and (iv) and it also has a slight edge advantage, thus it seems to be the medium method.

Now let us focus on the second type of figures (Figs. 14, 15, 16, 17, 18 and 19).

Fig. 14
figure 14

The results of the simulation for \(n=5\). The following notations are used: G index–Garuti’s compatibility index, C index–Cosine similarity index, ‘Weak’, ‘Modest’ and ‘Strong’ refers to the level of perturbation. Every subfigure shows the mean computed from 10000 pairwise comparison matrices

Full size image
Fig. 15
figure 15

The results of the simulation for \(n=6\). The following notations are used: G index–Garuti’s compatibility index, C index–Cosine similarity index, ‘Weak’, ‘Modest’ and ‘Strong’ refers to the level of perturbation. Every subfigure shows the mean computed from 10000 pairwise comparison matrices

Full size image
Fig. 16
figure 16

The results of the simulation for \(n=7\). The following notations are used: G index–Garuti’s compatibility index, C index–Cosine similarity index, ‘Weak’, ‘Modest’ and ‘Strong’ refers to the level of perturbation. Every subfigure shows the mean computed from 10000 pairwise comparison matrices

Full size image
Fig. 17
figure 17

The results of the simulation for \(n=8\). The following notations are used: G index–Garuti’s compatibility index, C index–Cosine similarity index, ‘Weak’, ‘Modest’ and ‘Strong’ refers to the level of perturbation. Every subfigure shows the mean computed from 10000 pairwise comparison matrices

Full size image
Fig. 18
figure 18

The results of the simulation for \(n=9\). The following notations are used: G index–Garuti’s compatibility index, C index–Cosine similarity index, ‘Weak’, ‘Modest’ and ‘Strong’ refers to the level of perturbation. Every subfigure shows the mean computed from 10000 pairwise comparison matrices

Full size image
Fig. 19
figure 19

The results of the simulation for \(n=10\). The following notations are used: G index–Garuti’s compatibility index, C index–Cosine similarity index, ‘Weak’, ‘Modest’ and ‘Strong’ refers to the level of perturbation. Every subfigure shows the mean computed from 10000 pairwise comparison matrices

Full size image

The results provided by the compatibility indices are similar to the previous ones, the main difference is that the models using additional ordinal information tend to perform better compared to the distances and rank correlations, especially for larger problems (n parameters). The most remarkable change is that the (ii) TOP2 model performs even better, and in many cases it provides the best values among the examined patterns. Also, the decreasing performance of the (v) 3-quasi-regular graphs seem to be even stronger for these metrics. However, the (vi) Union of two random edge-disjoint spanning trees model still outperforms all of the other models using additional information as well, except for the (ii) TOP2 model in some cases.

All in all we can conclude that the (vi) Union of two random edge-disjoint spanning trees model provided the best results without additional ordinal information. It is also shown that the best-second best ordinal information is indeed more valuable, than the best-worst or only the best case.

6 Conclusions and future research

We compared the weight vectors calculated from incomplete pairwise comparisons, such that the underlying graphs have approximately the same number of edges for each matrix size \(n=5,6,7,8,9,10.\) Based on the simulations we found that the presumed advantage of additional ordinal information on the ranking is realized only for the union of two star graphs, centered at the best and the second best items ((ii), TOP2). However, the union of two random edge-disjoint spanning trees (vi) outperforms all the other graphs according to both distance and rank correlation measures for every examined parameters, and only fell to second place in a few number of cases according to similarity indices, when the TOP2 model was the first one. This basically means that if there is an opportunity in a decision making problem to gain additional ordinal information, then the best and second best alternatives are preferred to the best and the worst ones. Also, the union of edge-disjoint spanning trees can result in as good as, or even better weight vectors than the ones calculated with additional information. In our view, these results of the paper are major contributions for AHP (and MADM) practitioners.

It is to be further investigated how the differences in the measures we applied, the Euclidean distance, Chebyshev distance, Manhattan distance, Kendall’s tau, Spearman’s rho, Garuti’s compatibility index, cosine similarity index and dice similarity index (in Figures 8-13, 14-19, A1-A6 and A7-A12) can be interpreted in practical decision making.

Can better graphs be found among the ones having the same number of edges?

A future research can investigate the different cardinalities of comparisons once the matrix size is fixed: how much can the result be improved by filling in more elements? Empirical (experimental) PCMs have been tested from this point of view without an emphasis on the graphs’ structure (Bozóki et al., 2013).

We considered some of the most intuitively-understandable closeness measures. Although there are infinitely many ways of measuring weight vectors’ similarity, it is not at all trivial which ones coincide with the subjective measures of most decision makers.

More dense graphs are subject to investigation, in particular, for larger dimensionalities (n). Does the same type/family of graphs (e.g. union of random edge-disjoint spanning trees) perform the best for incomplete PCMs of low, middle and high density? Can the graphs be constructed layer by layer?

Our analysis covers predetermined graphs only. We assumed that the whole questionnaire should be prepared a priori. However, one would expect that adaptive patterns could perform better compared to static ones. Once the decision maker provides some matrix elements, the remainder of the graph itself can be optimized in a dynamic way in order to maximize the expected information content of further responses.