Supplier–remanufacturing and manufacturer–remanufacturing in a closed-loop supply chain with remanufacturing cost disruption

Abstract

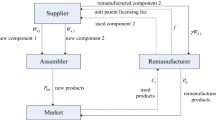
This paper studies remanufacturing cost disruption in a closed-loop supply chain consisting of a supplier, a manufacturer and a retailer. Specifically, the proposed work compares supplier–remanufacturing and manufacturer–remanufacturing modes with respect to equilibrium strategies and chain members’ profits, and analyzes the impacts of different disruption cases on each remanufacturing mode. Stackelberg game is applied to acquire equilibrium pricing decisions of each disruption case and it is found that the manufacturer–remanufacturing and supplier–remanufacturing modes have identical robustness. In manufacturer–remanufacturing mode, when the remanufacturing cost faces negative disruption, the manufacturer prefers to elevate the acquisition price and remanufacture more to improve profitability. In this case, the supplier will set a relatively lower wholesale price of components due to the marketing competition from the manufacturer, and the retailer can obtain more revenues. In supplier–remanufacturing mode, since the remanufactured components may cannibalize new component sales, the supplier will forgo some profits from new components in order to extract more profits from remanufacturing activities only if the negative disruption of remanufacturing cost is large enough. These results can provide a new insight into supplier–remanufacturing with cost disruption in a closed-loop supply chain.

Appendix

1.1 Proof of Proposition 1

The second-order derivative of $\Pi_{R}^{M}$ with respect to $p$ is $\partial^{2} \Pi_{R}^{M} /\partial p^{2} = - 2b < 0$, and thus $\Pi_{R}^{M}$ is concave in $p$. And the first-order derivative of the optimal price strategy can be solved as follows:

$$ \partial \Pi_{R}^{M} /\partial p = a + bw_{n} - 2bp = 0. $$

(27)

Taking the second-order partial derivatives of $\Pi_{M}^{M}$ with respect to $w_{n}$ and $r$, the Hessian matrix is

$$ H_{M}^{M} = \left( {\begin{array}{*{20}c} {\partial^{2} \Pi_{M}^{M} /\partial w_{n}^{2} } & {\partial^{2} \Pi_{M}^{M} /\partial w_{n} \partial r} \\ {\partial^{2} \Pi_{M}^{M} /\partial r\partial w_{n} } & {\partial^{2} \Pi_{M}^{M} /\partial r^{2} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} { - 2b} & 0 \\ 0 & { - 2v} \\ \end{array} } \right). $$

(28)

It can be found that, $\Pi_{M}^{M}$ is jointly concave in $w_{n}$ and $r$. And the first-order partial derivatives of $\Pi_{M}^{M}$ with respect to $w_{n}$ and $r$ are in the following:

$$ \left\{ {\begin{array}{*{20}c} {\frac{{\partial \Pi_{M}^{M} }}{{\partial w_{n} }} = a + bc_{n} + bw_{c} - 2bw_{n} = 0} \\ {\frac{{\partial \Pi_{M}^{M} }}{\partial r} = vs_{1} + vw_{c} - u - 2vr = 0} \\ \end{array} } \right.. $$

(29)

Afterward, taking the second-order derivative of $\Pi_{S}^{M}$ with respect to $w_{c}$, the equation $\partial^{2} \Pi_{S}^{M} /\partial w_{c}^{2} = - 2b - 4v < 0$ can be obtained, thus $\Pi_{S}^{M}$ is concave in $w_{c}$. The optimal price strategy can be solved as:

$$ \partial \Pi_{s}^{M} /\partial w_{c} = a - bc_{n} - 2u - 2vs_{1} + (b + 2v)c_{c} - 2(b + 2v)w_{c} = 0. $$

(30)

1.2 Proof of Proposition 2

Taking the second-order derivative of $\tilde{\Pi }_{R}^{MD}$ with respect to $p$, it can be obtained by $\partial^{2} \Pi_{R}^{MD} /\partial p^{2} = - 2b < 0$, thus $\tilde{\Pi }_{R}^{MD}$ is concave in $p$.

And the optimal price strategy can be solved as follows:

$$ \partial \tilde{\Pi }_{R}^{MD} /\partial p = a + bw_{n} - 2bp = 0. $$

(31)

Assuming that $q_{n} > q_{n}^{M*}$ and $q_{r} > q_{r}^{M*}$, and taking the second-order partial derivatives of $\tilde{\Pi }_{M}^{MD}$ with respect to $w_{n}$ and $r$, the Hessian matrix is given by

$$ H_{M}^{MD} = \left( {\begin{array}{*{20}c} {\partial^{2} \tilde{\Pi }_{M}^{MD} /\partial w_{n}^{2} } & {\partial^{2} \tilde{\Pi }_{M}^{MD} /\partial w_{n} \partial r} \\ {\partial^{2} \tilde{\Pi }_{M}^{MD} /\partial r\partial w_{n} } & {\partial^{2} \tilde{\Pi }_{M}^{MD} /\partial r^{2} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} { - 2b} & 0 \\ 0 & { - 2v} \\ \end{array} } \right). $$

(32)

Since $\partial^{2} \tilde{\Pi }_{M}^{MD} /\partial w_{n}^{2} = - 2b < 0$ and $\left| {H_{M}^{MD} } \right| = 4bv > 0$, $\tilde{\Pi }_{M}^{MD}$ is jointly concave in $w_{n}$ and $r$. Taking the first-order partial derivatives of $\tilde{\Pi }_{M}^{MD}$ with respect to $w_{n}$ and $r$, and letting the derivative be zero, we have

$$ \left\{ {\begin{array}{*{20}c} {\frac{{\partial \tilde{\Pi }_{M}^{MD} }}{{\partial w_{n} }} = \frac{1}{2}(a - 2bw_{n} + bc_{n} + bw_{c} + b\lambda_{n1} ) = 0} \\ {\frac{{\partial \tilde{\Pi }_{M}^{MD} }}{\partial r} = - u - 2vr + vw_{c} + vs_{1} - v\Delta c_{r} + v\lambda_{n1} - v\lambda_{r1} = 0} \\ \end{array} } \right.. $$

(33)

Subsequently, taking the second-order derivative of $\tilde{\Pi }_{S}^{MD}$ with respect to $w_{c}$, it can be expressed that $\partial^{2} \tilde{\Pi }_{S}^{MD} /\partial w_{c}^{2} = - 2b - 4v < 0$. Thus, $\tilde{\Pi }_{S}^{MD}$ is concave in $w_{c}$. Then the equilibrium results can be obtained by taking the first-order derivative of $\tilde{\Pi }_{S}^{MD}$ with respect to $w_{c}$.

And the proofs of other cases of $q_{n}$ and $q_{r}$ in Model MD are similar.

1.3 Proof of Proposition 3

The second-order derivative of $\Pi_{R}^{S}$ with respect to $p$ is $\partial^{2} \Pi_{R}^{S} /\partial p^{2} = - 2b < 0$, and thus $\Pi_{R}^{S}$ is concave in $p$. And the first-order derivative of $\Pi_{R}^{S}$ can be obtained as follows:

$$ \partial \Pi_{R}^{S} /\partial p = a + bw_{n} - 2bp = 0. $$

(34)

Then taking the second-order derivative of $E(\Pi_{M}^{S} )$ with respect to $w_{n}$, it can be obtained that $\partial^{2} E(\Pi_{M}^{S} )/\partial w_{n}^{2} = - 2b < 0$. Therefore, $E(\Pi_{M}^{S} )$ is concave in $w_{n}$. And the optimal price strategy can be solved as:

$$ \partial \Pi_{M}^{S} /\partial w_{n} = a + bc_{n} + bw_{c} - 2bw_{n} = 0. $$

(35)

Afterward, taking the second-order partial derivatives of $\Pi_{S}^{S}$, the Hessian matrix of $\Pi_{S}^{S}$ with respect to $w_{c}$ and $r$ is

$$ H_{S}^{S} = \left( {\begin{array}{*{20}c} {\partial^{2} \Pi_{S}^{S} /\partial w_{c}^{2} } & {\partial^{2} \Pi_{S}^{S} /\partial w_{c} \partial r} \\ {\partial^{2} \Pi_{S}^{S} /\partial r\partial w_{c} } & {\partial^{2} \Pi_{S}^{S} /\partial r^{2} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} { - 2b} & 0 \\ 0 & { - 2v} \\ \end{array} } \right). $$

(36)

Since $\partial^{2} \Pi_{S}^{S} /\partial w_{c}^{2} = - 2b < 0$ and $\left| {H_{S}^{S} } \right| = 4bv > 0$, $\Pi_{S}^{S}$ is strictly concave in $w_{c}$ and $r$. Then, the first-order partial derivatives of $\Pi_{S}^{S}$ with respect to $w_{c}$ and $r$ can be expressed as follows:

$$ \left\{ {\begin{array}{*{20}c} {\frac{{\partial \Pi_{S}^{S} }}{{\partial w_{c} }} = a - bc_{n} + bc_{c} - 2bw_{c} = 0} \\ {\frac{{\partial \Pi_{S}^{S} }}{\partial r} = vs_{2} - u - 2vr = 0} \\ \end{array} } \right.. $$

(37)

1.4 Proof of Proposition 4

The second-order derivative of $\tilde{\Pi }_{R}^{SD}$ with respect to $p$ is $\partial^{2} \tilde{\Pi }_{R}^{SD} /\partial p^{2} = - 2b < 0$, thus $\tilde{\Pi }_{R}^{SD}$ is concave in $p$. And the optimal price strategy can be solved as follows:

$$ \partial \tilde{\Pi }_{R}^{SD} /\partial p = a + bw_{n} - 2bp = 0. $$

(38)

Taking the second-order derivative of $\tilde{\Pi }_{M}^{SD}$ with respect to $w_{n}$, we can acquire $\partial^{2} \tilde{\Pi }_{M}^{SD} /\partial w_{n}^{2} = - 2b < 0$. Therefore, $\tilde{\Pi }_{M}^{SD}$ is concave in $w_{c}$. And the optimal price strategy can be solved as:

$$ \partial \tilde{\Pi }_{M}^{SD} /\partial w_{n} = a + bc_{n} + bw_{c} - 2bw_{n} = 0. $$

(39)

Subsequently, assume that $q_{n} > q_{n}^{S*}$ and $q_{r} > q_{r}^{S*}$, and taking the second-order partial derivatives of $\tilde{\Pi }_{S}^{SD}$ with respect to $w_{c}$ and $r$, the Hessian matrix is given by

$$ H_{S}^{SD} = \left( {\begin{array}{*{20}c} {\partial^{2} \tilde{\Pi }_{S}^{SD} /\partial w_{c}^{2} } & {\partial^{2} \tilde{\Pi }_{S}^{SD} /\partial w_{c} \partial r} \\ {\partial^{2} \tilde{\Pi }_{S}^{SD} /\partial r\partial w_{c} } & {\partial^{2} \tilde{\Pi }_{S}^{SD} /\partial r^{2} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} { - 2b} & 0 \\ 0 & { - 2v} \\ \end{array} } \right). $$

(40)

Since $\partial^{2} \tilde{\Pi }_{S}^{SD} /\partial w_{n}^{2} = - 2b < 0$ and $\left| {H_{S}^{SD} } \right| = 4bv > 0$, $\tilde{\Pi }_{S}^{SD}$ is jointly concave in $w_{c}$ and $r$.

And the proofs of other cases of $q_{n}$ and $q_{r}$ in Model SD are analogous.

1.5 Proof of Corollary 1

In Model MD, since $\tilde{w}_{c}^{MD*(3)} = \frac{{a - bc_{n} + (b + 2v)c_{c} - 2vs_{1} - 2u}}{2b + 4v}$ and $w_{c}^{M*} = \frac{{a - bc_{n} + (b + 2v)c_{c} - 2vs_{1} - 2u}}{2b + 4v}$, it can be obtained that $\tilde{w}_{c}^{MD*(3)} = w_{c}^{M*}$.

Moreover, to prove $\tilde{\Pi }_{M}^{MD*(3)} > \Pi_{M}^{M*}$, it has to show that

$$ \tilde{\Pi }_{M}^{MD*(3)} - \Pi_{M}^{M*} = \frac{{ - 4v(b + 2v)\Delta c_{r} [v(a - bc_{n} ) + 2(b + v)(u + vs_{1} ) + v(b + 2v)c_{c} ]}}{{16v(b + 2v)^{2} }} > 0. $$

(41)

After simplification, this reduces to showing that $\Delta c_{r} < 0$.

Therefore, it can be obtained that, if $\Delta c_{r} < 0$, then $\tilde{\Pi }_{M}^{MD*(3)} > \Pi_{M}^{M*}$.

And the proofs of the relationships of other prices, quantities and profits are analogous.

1.6 Proof of Corollary 2

Since $\Delta c_{r} < - (1 + \frac{b}{2v})\lambda_{n2} - \lambda_{r1}$ holds in case 1, it can be obtained that

$$ \begin{aligned} \tilde{w}_{c}^{*(1)} & = \frac{{a - bc_{n} - 2(u + vs_{1} ) + (b + 2v)(c_{c} + \lambda_{n2} ) + 2v(\Delta c_{r} + \lambda_{r1} )}}{2(b + 2v)} \\ & < \frac{{a - bc_{n} - 2(u + vs_{1} ) + (b + 2v)c_{c} }}{2(b + 2v)} = \tilde{w}_{c}^{*(2)} . \\ \end{aligned} $$

(42)

Meanwhile, as $\Delta c_{r} > (1 + \frac{b}{2v})\lambda_{n1} + \lambda_{r2}$ is satisfied in case 5, it can be given by

$$ \begin{aligned} \tilde{w}_{c}^{*(5)} & = \frac{{a - bc_{n} - 2(u + vs_{1} ) - (b + 2v)(\lambda_{n1} - c_{c} ) + 2v(\Delta c_{r} - \lambda_{r2} )}}{2(b + 2v)} \\ & > \frac{{a - bc_{n} - 2(u + vs_{1} ) + (b + 2v)c_{c} }}{2(b + 2v)} = \tilde{w}_{c}^{*(4)} . \\ \end{aligned} $$

(43)

Moreover, since $\tilde{w}_{c}^{*(2)} = \tilde{w}_{c}^{*(3)} = \tilde{w}_{c}^{*(4)} = \frac{{a - bc_{n} - 2(u + vs_{1} ) + (b + 2v)c_{c} }}{2(b + 2v)}$,

Then we can get that $\tilde{w}_{c}^{*(1)} < \tilde{w}_{c}^{*(2)} = \tilde{w}_{c}^{*(3)} = \tilde{w}_{c}^{*(4)} < \tilde{w}_{c}^{*(5)}$.

The proofs of the relationships of others prices, quantities and profits are analogous.

1.7 Proof of Corollary 3

As $\Delta c_{r} > (1 + \frac{b}{2v})\lambda_{n1} + \lambda_{r2}$ holds in case 5, to prove $\tilde{w}_{c}^{MD*} < \tilde{w}_{c}^{SD*}$, it has to examine that

$$ \begin{aligned} \tilde{w}_{c}^{MD*} - \tilde{w}_{c}^{SD*} & = \frac{{a - bc_{n} - 2(u + vs_{1} ) - (b + 2v)(\lambda_{n1} - c_{c} ) + 2v(\Delta c_{r} - \lambda_{r2} )}}{2(b + 2v)} - \frac{{a - bc_{n} + bc_{c} + b\lambda_{n1} }}{2b} < 0 \\ & = \frac{{ - 2b(u + vs_{1} ) - 2b(b + 2v)\lambda_{n1} + 2bv(\Delta c_{r} - \lambda_{r2} ) - 2v(a - bc_{n} )}}{2b(b + 2v)} < 0, \\ \end{aligned} $$

(44)

After simplification, this reduces to showing that

$$ \Delta c_{r} < \frac{{v(a - bc_{n} ) + b(u + vs_{1} ) + (b + 2v)b\lambda_{n1} }}{bv} + \lambda_{r2} . $$

(45)

Therefore, it can be obtained that if $\Delta c_{r} < \frac{{v(a - bc_{n} ) + b(u + vs_{1} ) + (b + 2v)b\lambda_{n1} }}{bv} + \lambda_{r2}$ holds, then $\tilde{w}_{c}^{MD*} < \tilde{w}_{c}^{SD*}$. And the proofs of the relationships of the prices, quantities and profits are analogous.

1.8 Proof of Corollary 4

If $\Delta c_{r} > (1 + \frac{b}{2v})\lambda_{n1} + \lambda_{r2}$ is satisfied in case 5, it can be obtained that

$$ \begin{aligned} \tilde{\Pi }_{R}^{MD*} - \tilde{\Pi }_{R}^{SD*} & = \frac{{[(b + 4v)(a - bc_{n} ) + 2b(u + vs_{1} ) - b(b + 2v)(\lambda_{n1} + c_{c} ) - 2bv(\Delta c_{r} - \lambda_{r2} )]^{2} }}{{64b(b + 2v)^{2} }} - \frac{{(a - bc_{n} - bc_{c} - b\lambda_{n1} )^{2} }}{64b} \\ & { = }\frac{{[(b + 4v)(a - bc_{n} ) + 2b(u + vs_{1} ) - b(b + 2v)(\lambda_{n1} + c_{c} ) - 2bv(\Delta c_{r} - \lambda_{r2} )]^{2} - (a - bc_{n} - bc_{c} - b\lambda_{n1} )^{2} (b + 2v)^{2} }}{{64b(b + 2v)^{2} }}, \\ \end{aligned} $$

Therefore, to prove $\tilde{\Pi }_{R}^{MR*} > \tilde{\Pi }_{R}^{SR*}$, it has to show that

$$ \begin{aligned} & [(b + 4v)(a - bc_{n} ) + 2b(u + vs_{1} ) - b(b + 2v)(\lambda_{n1} + c_{c} ) \\ & \quad - 2bv(\Delta c_{r} - \lambda_{r2} )]^{2} > (a - bc_{n} - bc_{c} - b\lambda_{n1} )^{2} (b + 2v)^{2} , \\ & (b + 4v)(a - bc_{n} ) + 2b(u + vs_{1} ) - b(b + 2v)(\lambda_{n1} + c_{c} ) \\ & \quad - 2bv(\Delta c_{r} - \lambda_{r2} ) > (a - bc_{n} - bc_{c} - b\lambda_{n1} )(b + 2v). \\ \end{aligned} $$

After simplification, this reduces to showing that

$$ \Delta c_{r} < \frac{{v(a - bc_{n} ) + b(u + vs_{1} )}}{bv} + \lambda_{r2} . $$

(46)

Moreover, as $\Delta c_{r} > (1 + \frac{b}{2v})\lambda_{n1} + \lambda_{r2}$ is satisfies in case 5, we can get $\tilde{\Pi }_{R}^{MR*} > \tilde{\Pi }_{R}^{SR*}$, when $(1 + \frac{b}{2v})\lambda_{n1} + \lambda_{r2} < \Delta c_{r} < \frac{{v(a - bc_{n} ) + b(u + vs_{1} )}}{bv} + \lambda_{r2}$ holds.

Similarly, the relationships of others prices, quantities and profits in Model MD and Model SD can be proved.

1.9 The equilibrium results in Model MD and Model SD

1. The equilibrium results in Model MD (Tables 8, 9).

Table 8 The equilibrium quantity and profits in Model MD

Table 9 The equilibrium manufacturer’s profit in Model MD

2. The equilibrium results in Model SD (Tables 10, 11).

Table 10 The equilibrium quantities and profits in Model SD

Table 11 The equilibrium supplier’s profit in Model SD