A robust-heuristic optimization approach to a green supply chain design with consideration of assorted vehicle types and carbon policies under uncertainty

Abstract

Adoption of carbon regulation mechanisms facilitates an evolution toward green and sustainable supply chains followed by an increased complexity. Through the development and usage of a multi-choice goal programming model solved by an improved algorithm, this article investigates sustainability strategies for carbon regulations mechanisms. We first propose a sustainable logistics model that considers assorted vehicle types and gas emissions involved with product transportation. We then construct a bi-objective model that minimizes total cost as the first objective function and follows environmental considerations in the second one. With our novel robust-heuristic optimization approach, we seek to support the decision-makers in comparison and selection of carbon emission policies in supply chains in complex settings with assorted vehicle types, demand and economic uncertainty. We deploy our model in a case-study to evaluate and analyse two carbon reduction policies, i.e., carbon-tax and cap-and-trade policies. The results demonstrate that our robust-heuristic methodology can efficiently deal with demand and economic uncertainty, especially in large-scale problems. Our findings suggest that governmental incentives for a cap-and-trade policy would be more effective for supply chains in lowering pollution by investing in cleaner technologies and adopting greener practices.

1 Introduction

The integration of sustainability issues into supply chain (SC) management has progressed remarkably, most of it focused on the areas of the green supply chain (GSC) and the sustainable supply chain (SSC) (Tang and Zhou 2012; Golinska-Dawson et al. 2018; Heydari et al. 2020). Increasing concerns about the environmental impacts and international and government regulations have attracted research attention to the GSC problems beyond merely economic aspects (Ivanov et al. 2019). In an GSC, the environmental impacts from SCs need to be minimized complementing total cost minimization (Rezaee et al. 2017). Moreover, social aspects in SCs became a trend and lead to introducing the SSC network (Carter and Rogers 2008; Pavlov et al. 2019). In general, when the financial, environmental and social impacts of the SC are considered simultaneously, the traditional SC shifts toward the SSC. The transition from the traditional goals of the SC to the new sustainable objectives is also identified as the company’s competitive advantage (Dubey et al. 2015; Giannakis and Papadopoulos 2016).

Improvements in operating costs efficiency and service levels while paying special attention to the environmental, economic, and social considerations in the SC belong to major requirements to succeed in highly competitive markets (Golinska-Dawson et al. 2018; Brandenburg et al. 2019). Due to environmental pollution and increased global warming, government and international bodies have introduced laws obliging companies to address environmental issues. One of the most important parts of new regulations is reducing carbon emissions/footprint that improves the business’s environmental performance (Golinska and Romano 2012). In an SC, this will bring the integrity of all parts of the SC in social commitments. A carbon footprint reduction project is therefore of a global economic importance (Fahimnia and Jabbarzadeh 2016).

A recent European Commission report illustrates that the amount of transport gas emissions has been continually increasing, and if no action is taken, transport emissions could make up more than 30% of total EU gas emissions by the end of 2020. The report also demonstrates that 93–95% of greenhouse gas emissions resulting from transport operations are composed of CO$_2$ (Eurostat 2019). The European Union Emissions Trading System (EU-ETS) is a tool that uses a tiered method for calculating emissions, linked to necessary uncertainty ranges that are supported in the EU climate policy’s monitoring and reporting guidelines. The EU-ETS is identified as a powerful system for deducting greenhouse gas emissions especially CO$_2$ emissions cost-effectively (EU climate actions 2019).

SC’s CO$_2$ emissions can be seen in the various components, including raw material procurement, product manufacturing, distribution and retail, and disposal and recycling (Zhen et al. 2019; Golinska et al. 2015). Figure 1 illustrates that most of the CO$_2$ emissions are accounted in transportation and logistics processes of GSCs and SSCs, according to a survey through 215 SC companies in Europe (GSCmonitor 2015). From GSC and SSC point of view, Mohammed et al. (2017) concede that although the sources of CO$_2$ emissions have been broadly investigated in academic research, the decisions regarding types of vehicles used is critical in real-world transportation systems, and this fact was left ignored in most of the GSC and SSC models. Moreover, an increasing uncertainty of demand and economic environments represent a research challenge for design of GSC and SSC (Brandenburg and Rebs 2015; Allaoui et al. 2019).

Fig. 1

Areas of focus for the calculation of carbon emissions in GSC and SSC companies (Based on GSCmonitor (2015))

Recent literature suggests that instead of choosing an efficient policy from the existing carbon emission plans, an applicable model for the GSC and SSC could be created by considering uncertainty features in the key parameters of the model, especially demand and related costs (He et al. 2019). To this end, we aim to design an GSC by employing a robust-heuristic optimization method to cope with demand and economic uncertainty and considering assorted vehicle types. Robust optimization is one of the branches of optimization theory that cope with uncertain optimization problems. In scenario-based robust optimization, this method combines scenario-based description of problem data with the solution formulations like goal programming. This approach tries to generate solutions that are less sensitive to realizations of the model data. Robust optimization has some advantages comparing other approaches such as stochastic programming (Mulvey et al. 1995).

We contribute to literature by offering a comprehensive approach to minimize carbon emissions in most of the SC processes and considering diversity of vehicle types and uncertainty in SC costs. We present a bi-objective model that focuses on a specific capacity for an environmentally-friendly SC and carbon emissions. The proposed bi-objective model is converted to a single-objective one that aims to solve the problem by using improved multi-choice goal programming (IMCGP). Since the model is an NP-hard one in large-scale problems, for reducing the solving time and complexity of the problem, we employ a heuristic method combined with the improved IMCGP. To test and examine our model, two carbon reduction policies—namely carbon-tax and cap-and-trade—are compared in a real case study.

The remainder of this paper is organised as follows. In Sect. 2, we present a detailed literature review about the topic. In Sect. 3, the problem is defined and formulated. We explain our novel solution approach in Sect. 4.6. A real case study and related numerical tests are provided in Sect. 5, illustrating the effectiveness of the proposed model. Managerial insights are provided in Sect. 7. In Sect. 8, we conclude with summarizing major insights of our study and outlining possible future research directions.

2 Literature review

In this section, we provide a brief review of extant literature in GSC and CO$_2$ footprint modeling and sustainability considerations in SC modeling. We also develop a conceptual linkage between these subjects to provide the contributions expected from this study. A summary of recent literature on these topics is presented in Table 1.

2.1 Green supply chain and CO$_2$ footprint modeling

In recent years, a greater focus on carbon emissions and footprints can be observed in GSC models (Mohammed et al. 2018; Tirkolaee et al. 2020). Carbon footprint measurements are needed to provide a reliable estimate of the total amount of greenhouse gas emissions released in the life cycle of products and services along the SC. These estimations can include various elements from raw material extraction to production, distribution, storage, and recycling (Plassmann et al. 2010). Chen and Chen (2017) study the carbon footprint and allocation of responsibility involved with the production stage. Despite the advantage of optimizing the social value of the GSC, they only consider single-period and single-product network and ignore the transportation and holding processes as the source of carbon emissions. In another study evaluating environmental implications in the SC, Bazan et al. (2015) minimize the total cost of the reverse logistics network, considering carbon footprint and production energy simultaneously. The green concept has also been employed for green inventory routing problems with consideration of several interval fuel consumptions (Franco et al. 2016, 2017).

In a review article, Dekker et al. (2012) discuss green logistics and the integration of different environmental aspects into green logistics, the most important of which is carbon emissions in transportation. Du et al. (2016) also examine low-carbon production and its implementation in the SC. Their suggested that a commercial system according to energy consumption can still be profitable in the case of low-carbon production. Hao et al. (2017) investigate the amount of greenhouse gas emissions and energy consumption, using a life cycle assessment framework under recycling options. The authors develop a low-carbon design approach to estimate the carbon footprint at each stage of the product life cycle. Aiming to minimize carbon footprint in a reverse logistics network, Kannan et al. (2012) propose a single-product, single-period linear integer programming model. Moreover, Zhao et al. (2013) develop a mathematical model to minimize the level of carbon emissions in transportation system and distribution centers. However, their model lacks the consideration of uncertainty in its parameters—a distinctive and substantial contribution made by our study.

Our literature analysis demonstrates that the consideration of uncertainty has been growing for the recent years. For instance, in a study aimed at designing an SSC network under the uncertainty of capacity of suppliers, producers, and warehouses, Shaw et al. (2016) propose a model including greenhouse gas emissions and carbon trading issues. The authors also contemplate demand uncertainty in their model. Aljuneidi and Bulgak (2020) present an integrated approach to designing a reverse logistics network for a sustainable manufacturing company. Their model minimizes carbon emissions and transportation distances between facilities by considering a hybrid production and reproduction system. Moreover, Reddy et al. (2019) consider a reverse-logistic network design (RLND) and develop a mixed-integer linear programming (MILP) model in a multi-period configuration. Their proposed network focuses on the choice of vehicle type and carbon emissions through operations and transportation by defining a corresponding binary variable that is equal to one when a vehicle type is selected between two nodes. Although their model has the advantage of vehicle type selection, the model is developed for a single period and does not consider any uncertainty in the main parameters of the model. Our review of the literature about GSC models also shows that the majority of the studies develop a multi-objective optimization problem and incorporate uncertainty in a non-linear context. They solve the proposed problem using a single-objective model converted from a multi-objective one (Govindan et al. 2020).

2.2 Sustainability considerations in supply chain modelling

We now turn to multi-objective issues in designing SSC. Given the growing concern over sustainability in recent years, researchers and practitioners began to incorporate social and environmental factors into SC design in addition to economic factors. One of the main objective is to develop a model that can simultaneously cover economic, social, and environmental perspectives. While most research has focused on the economic aspects of SCs (Jahani et al. 2019), some recent studies have taken environmental aspects into account (Moreno-Camacho et al. 2019). Researchers believe that the use of sustainable SC management (SSCM) will bring several advantages for the organizations such as reducing environmental risks and pollution (Ansari and Kant 2017) and improving customer relationships (Sauer and Seuring 2019).

The sustainability issues can be addressed by defining a multi-objective optimization model for an SC. Accordingly, Arampantzi and Minis (2017) consider a multi-objective mathematical framework for an SSC design, including significant decisions in high-performance SC design or redesign. Their model complies with all three goals of the SSC, i.e., economic, social, and environmental areas. Jabbarzadeh et al. (2018) present a hybrid approach to designing an SSC network that is flexible in the face of random disturbances. They also employ a fuzzy c-means clustering method to measure and evaluate suppliers’ sustainability performance. Although a new methodology is developed in their study for the SSC, the model considers a single-period and single-product problem. Considering a multi-product and multi-period reverse SC, John et al. (2017) develop an MILP model by integrating the carbon emission cost of transport activities. This study has ignored carbon emissions generated in the production and holding activities, and the uncertainty features in the main parameters like demand.

Taking uncertainty into account is a common characteristic of recent modeling approaches for SSC design. Habibi et al. (2017) propose a multi-objective mathematical model for an SSC network under an uncertain return product parameter. In their RLND model, they propose the first objective as minimization of total cost, including the cost of moving facilities, cost of transfer stations, allocation costs of facilities, shipment costs, recovery activities costs, and penalty costs. The second objective of their model deliberates the minimization of environmental impacts and visual pollution. Zahiri et al. (2018) develop another multi-objective mixed-integer nonlinear programming (MINLP) model for an SSC network under the uncertain demand and supply parameters. They propose the first objective as the minimization of total cost, incorporating inventory costs, location and allocation costs of facilities, manufacturing costs, shipment costs, procurement costs, and fixed ordering costs. The second objective of their model is defined as the minimization of environmental impacts, and the third objective complies with the maximization of an SC’s responsiveness. This research only models a single-product network in which the sources of carbon emissions are ignored in the environmental impacts. In the case of sustainability and the RLND model, many studies can be found regarding a sustainable closed-loop SC network (e.g. Govindan et al. (2016); Soleimani et al. (2017); Sahebjamnia et al. (2018)). Also, some recent motivating studies consider green and sustainable closed-loop SC (see Zhen et al. (2019); Yun et al. (2020); Esmaeili et al. (2020)).

Table 1 Recent studies modeling GSC and SSC under uncertainty

2.3 Contributions of the study

The literature review illustrates that although there are many studies in the GSC and SSC fields, there are still some gaps. For example, some studies ignore considering the multiple sources of carbon emissions (see the models provided by Jindal and Sangwan (2017), Chen and Chen (2017), John et al. (2017), Reddy et al. (2019) and Govindan et al. (2020)). Even if some studies consider carbon emissions in various processes of the SC, they ignore the consideration of different types of vehicles in the transportation. We demonstrated the remarkable effect of this assumption in the Introduction Section (see the models developed by Soleimani et al. (2017), Yadollahinia et al. (2018), Yavari and Geraeli (2019), Banasik et al. (2019) and Zahiri et al. (2018)). We also insist on considering uncertainty features in all main parameters of a GSC or SSC model that is ignored in several relevant models (Chibeles-Martins et al. 2016; John et al. 2017; Reddy et al. 2019; Franco and Alfonso-Lizarazo 2020). Finally, researchers have had less attention to compare different carbon policies and they usually focused on carbon cap-and-trade policy (see Kaur and Singh (2018) and Gholizadeh et al. (2020)).

We contribute to closing these research gaps in multiple ways. Our article investigates sustainability strategies for carbon regulations mechanisms. We first propose a sustainable logistics model that considers assorted vehicle types and gas emissions involved with product transportation. We then construct a bi-objective model that minimizes total cost as the first objective function and follows environmental considerations in the second one. With our novel robust-heuristic optimization approach, we offer a decision-making support in comparison and selection of carbon emission policies in GSCs in complex settings with assorted vehicle types, demand and economic uncertainty. Due to the existence of nonlinear constraints arising from uncertain parameters, in our proposed MINLP model, we employ a robust optimization approach along with a heuristic method which allows reducing the computational time at different levels of uncertainty. Distinctively, in contrast to the consideration of uncertainty in demand and costs in the existing GSC and SSC models, our model has the advantage of contemplating uncertainty in all main costs associated with an SC (i.e. production, transportation, ordering, holding, and shortage costs). We deploy our model in a case-study to evaluate and analyse two carbon reduction policies, i.e., carbon-tax and cap-and-trade policies. The results demonstrate that our robust-heuristic methodology can efficiently deal with demand and economic uncertainty, especially in large-scale problems. Selecting optimal vehicle types with the lowest carbon emissions is another original feature of our study that can help managers to deduct carbon emissions more effectively in their GSCs. Our findings suggest that governmental incentives for a cap-and-trade policy would be more effective for supply chains in lowering pollution by investing in cleaner technologies and adopting greener practices.

3 Problem statement

In this study, we consider a CO$_2$ footprint network and an emissions-reduction business scenario. We study a multi-period setting for a multi-product and multi-tier SC with multiple suppliers and multi-carrier transport. The problem involves ordering, manufacturing, and shipping products using the carriers/vehicles and is aimed at minimizing total purchasing costs while incorporating carbon emissions costs. This is achieved by optimally allocated orders among potential suppliers through different types of vehicles. Figure 2 represents the proposed classification of carbon emission sources in SC processes. It can be observed in Fig. 2 that total carbon emissions include two parts: (1) operation-related carbon emissions and (2) transportation-related carbon emissions. The operation-related emissions are derived from two causes: production (how items are procured, and the quantity produced) and storage (holding inventory). The transportation-related emissions are derived from the vehicles and their types (the mileage, carrying load, and distance traveled by each vehicle).

Fig. 2

Supply chain network and carbon emission sources

Figure 3 shows the sustainable logistics framework used in this study to highlight the SC network and the carbon footprint emissions from each SC process. The range and bounds of carbon emissions are of great importance in determining and calculating both direct and indirect emissions throughout the SC. Without a clear identification of this range, no footprint measurement or reporting would be possible. One major advantage of this framework is that it calculates not only the carbon emissions from the viewpoint of the procurement of products but also from the perspectives of holding inventory and logistics, providing a holistic view of the SC (Paksoy et al. 2019).

Fig. 3

Sustainable logistics framework used in this study (based on Lee (2011))

Carbon footprint recovery options are considered as carbon cap-and-trade policies. Constant gas releases are associated with the selected vehicles and their types. The variable gas emissions related to a vehicle is a function of the distance covered by the vehicle, its mileage, the type of fuel consumed by the vehicle, and the load transported by the vehicle. Carbon-and-trade policy is used to manage and control greenhouse gas emissions, in which a constant share is permitted for the SC. The carbon market can be considered a potential option for selling government-granted allotments of CO$_2$ outputs.

Sustainable logistics planning has two principal objectives, namely minimizing the total cost and maximizing the vehicle’s transportation performance (Dekker et al. 2012). The plan is aimed at reducing carbon emissions by determining SC’s inventory levels under uncertainty and carbon policies (carbon-tax and cap-and-trade). Given that each policy has its merits, the comparison of the policies is also investigated in the plan.

Since demand and costs associated with a product can be impacted by unexpected events like unstable economic situations, it is difficult to predict the exact distribution of the product and its future demands and costs. Hence, there is no guarantee that the distribution of probabilities, particularly in our multi-period problem, will be stabilized. Despite the availability of enough data to produce valid scenarios, it is challenging to estimate future demands and costs regarding each scenario. Consequently, we develop a probabilistic model in our study to formulate the uncertainty of these parameters in each scenario.

4 Model

The list of indicators, variables, and symbols used in our proposed mathematical model are presented as follows:

4.1 List of indices and sets

i :

Products $i=1,2,\ldots ,I$

j :

Suppliers $j=1,2,\ldots ,J$

t :

Time periods $t=1,2,\ldots ,T$

v :

Vehicle $v=1,2,\ldots ,V$

s :

Scenarios $s=1,2,\ldots ,S$

4.2 List of parameters

$\overline{D}_{its}$ :

Demand for product i in period t under scenario s.

$\overline{CP}_{ijts}$ :

Procurement cost of product i from supplier j in period t under scenario s.

$\overline{CT}_{jvts}$ :

Transportation cost from supplier j using vehicle v in period t under scenario s.

$\overline{CO}_{ijts}$ :

Ordering cost of product i procured from supplier j in period t under scenario s.

$\overline{CH}_{its}$ :

Holding inventory cost of product i in period t under scenario s.

$\overline{CS}_{its}$ :

Shortage cost of product i in period t under scenario s.

$Cap_{ijt}$ :

Capacity of supplier j to provide product i in period t.

$\sigma _{jv}$ :

Capacity of vehicle v available for supplier j

$N_{jvt}$ :

Total number of vehicle v available for supplier j in period t.

$F_{ijvt}$ :

Amount of carbon gas emissions in executing a lot size of X units of product i procured from supplier j by using vehicle v in period t.

$\tau$ :

Amount of permitted carbon gas emissions during the entire planning horizon.

cp :

Price on carbon per unit.

$\overline{\delta }_{vts}$ :

Carbon emissions factor caused by vehicle v in period t under scenario s.

$EO_t$ :

Amount of carbon gas emissions due to placing an order in period t.

$EH_t$ :

Amount of carbon gas emissions due to holding a unit of a product at a warehouse in period t.

$L_{ivt}$ :

Lead time of supplier j using vehicle v in period t.

$EL_{it}$ :

Lead time lower tolerance for product i in period t.

$UL_{it}$ :

Lead time upper tolerance for product i in period t.

$DD_j$ :

Distance between supplier j and the buyer.

$M_{vt}$ :

Mileage (km per liter) of vehicle v at the beginning of period t.

M :

Big number.

$p_s$ :

Probability of the occurrence of scenario s.

4.3 List of decision variables

$\pi$ :

Extra or spare carbon credit sold or bought over the entire planning horizon.

$X_{ijvts}$ :

Quantity of product i procured by supplier j using vehicle v in period t under scenario s.

$S_{its}$ :

Quantity of shortage in product i in period t under scenario s.

$I_{its}$ :

Inventory level of product i carried from period t to $t+1$ under scenario s.

$U_{ijvt}$ :

Binary variable equals to 1 if product i is supplied by supplier j using vehicle v in period t; 0 otherwise.

$Y_{jvts}$ :

Binary variable equals to 1 if vehicle v is chosen with the lowest carbon emission for buying from supplier j during period t under scenario s; otherwise 0.

4.4 List of assumptions

The main assumptions of the problem, according to the literature of robust heuristics models (e.g. Kaur and Singh (2018); Gholizadeh et al. (2020)) are presented as follows:

• Demand and main costs (procurement, transportation, ordering, and holding inventory costs) are considered uncertain in a scenario-based stochastic approach.

• Sustainable procurement is modelled using uncertain data, delay in delivery, and shortage in supply.

• The supplier and the vehicles capacities are known.

• Any plant and production process in the SC network can be assumed as a supplier with limited capacity in the model.

We also add the following assumptions with respect to our new contributions to literature:

• The procurement and logistics processes represent real-time demand or capacity changes for each period.

• In logistics, an empty vehicle (with no load) releases constant CO$_2$, whereas the variable CO$_2$ emission is a function of size, distance, and the mileage of vehicles.

4.5 Proposed formulation

The total cost of procurement is represented in the first objective function (Eq. 1) and contains production, shipping, ordering, inventory, shortage, and carbon selling/buying income/cost. The lowest carbon gas emission coverage related to vehicle selection is addressed in the second objective function (Eq. 2).

$$\begin{aligned} min \, Obj_1 =&\sum _{i}\sum _{j}\sum _{t}\sum _{s}\sum _{v}\overline{CP}_{ijts} X_{ijvts} + \sum _{i}\sum _{j}\sum _{t}\sum _{s}\sum _{v}\overline{CO}_{ijts} U_{ijvt} \nonumber \\&+ \sum _{i}\sum _{j}\sum _{v}\sum _{t}\sum _{s}\overline{CT}_{jvts} DD_j X_{ijvts} + \sum _i\sum _t\sum _s\overline{CH}_{its} I_{its} \nonumber \\&+ \sum _{i}\sum _{t}\sum _{s}\overline{CS}_{its} S_{its} + \pi cp \end{aligned}$$

(1)

$$\begin{aligned} min \, Obj_2 =&\sum _{j}\sum _{v}\sum _{t}\sum _{s}Y_{jvts} DD_j \overline{\delta }_{vts} \end{aligned}$$

(2)

The main constraints of the proposed optimization model are defined in Eqs. (3)–(12) and explained in Table 2. Equation (7) is the most important constraint of the model and used to plan and control carbon emissions in both carbon-tax and cap-and-trade policies. We employ this constraint to examine our first contribution listed in Sect. 2.3. The index v in all designated parameters and variables is also used for incorporating the contributions of the study regarding the consideration of assorted vehicle types and the lowest levels of carbon emissions in vehicles and transportation systems.

$$\begin{aligned}&I_{i(t-1)s} - S_{i(t-1)s} + \sum _j\sum _v X_{ijvts} - I_{its} + S_{its} = \overline{D}_{its} \qquad \forall i, t, s&\end{aligned}$$

(3)

$$\begin{aligned}&I_{i(t-1)s} - S_{i(t-1)s} \le \overline{D}_{its} U_{ijvt} \qquad \forall i, j, v, t, s&\end{aligned}$$

(4)

$$\begin{aligned}&\sum _v\sum _s X_{ijvts} \le Cap_{ijt} \qquad \forall i, j, t&\end{aligned}$$

(5)

$$\begin{aligned}&\sum _i\sum _s X_{ijvts} \le \sigma _{jv} N_{jvt} \qquad \forall j, v, t&\end{aligned}$$

(6)

$$\begin{aligned}&\sum _{i}\sum _{j}\sum _{t}\sum _{s}\sum _{v} \left( F_{ijvt} X_{ijvts} + \frac{DD_j}{M_{vt}} \overline{\delta }_{vt}\right) U_{ijvt} + \sum _{i}\sum _{j}\sum _{v}\sum _{t} EO_t U_{ijvt}&\end{aligned}$$

(7)

$$\begin{aligned}&+ \sum _{i}\sum _{t}\sum _{s} EH_t I_{its} = \pi + \tau&\nonumber \\&L_{ivt} U_{ijvt} \le UL_{it} + M(1-U_{ijvt}) \qquad \forall i,j,v,t&\end{aligned}$$

(8)

$$\begin{aligned}&L_{ivt} U_{ijvt} \ge EL_{it} + M(1-U_{ijvt}) \qquad \forall i,j,v,t&\end{aligned}$$

(9)

$$\begin{aligned}&\sum _{j} Y_{jvts} \ge 1 \qquad \forall v, t&\end{aligned}$$

(10)

$$\begin{aligned}&\overline{X}_{ijvts}, \overline{I}_{its}, \overline{b}_{its}, \pi \ge 0 \qquad \forall i, j, v, t, s&\end{aligned}$$

(11)

$$\begin{aligned}&U_{ijvt}, Y_{jvts} \in \{0,1\} \qquad \forall i, j, v, t, s&\end{aligned}$$

(12)

Table 2 The main constraints of the proposed model and their explanations

According to the proposed mathematical formulation introduced in Sect. 4.5, multiplying a continuous variable by a binary variable, formulated in Eq. (7), leads to an MINLP model. To solve this problem, a traditional method is normally introduced in the MINLP models’ literature to turn the model into an MILP model (Jahani et al. 2018).

4.6 Traditional linearization approach

Regarding the linearization of the nonlinear terms of an MINLP model, several linearization constraints can be defined as follows (Gholizadeh et al. 2018):

$$\begin{aligned}&\sum _s X_{ijvts} \le U_{ijvt} M \qquad \forall i, j, v, t&\end{aligned}$$

(13)

$$\begin{aligned}&\sum _s \xi _{ijvts} \le \sum _s X_{ijvts} \qquad \forall i, j, v, t&\end{aligned}$$

(14)

$$\begin{aligned}&\sum _s \xi _{ijvts} \ge \sum _s X_{ijvts} - (1 - U_{ijvt}) * M \qquad \forall i, j, v, t&\end{aligned}$$

(15)

Where $\xi _{ijvts}$ is a continuous positive auxiliary variable and M is a sufficiently large positive number.

4.7 Robust optimization counterpart

Every GSC requires information management that necessitates consideration of several issues regarding input data in SC modelling (Kolinski et al. 2019). According to Bairamzadeh et al. (2018), input data can include three types of uncertainties based on the amount of available information: (1) randomness, (2) epistemic, and (3) deep uncertainty. Randomness uncertainty occurs once there is adequate and valid historical data for estimating the probability distribution. Epistemic uncertainty is often characterized by the deficiency of information in input data. This kind of uncertainty is generally presented in the form of judgmental data from linguistic features, and the data may be collected by experienced professionals. Finally, deep uncertainty is related to the lack of information necessary to predict the objective or subjective probability of future conditions (Bairamzadeh et al. 2018). Figure 4 demonstrates the classification of uncertainty types and suitable modeling methods based on the nature of uncertainty.

Since we assume data availability to estimate the probability distribution of the parameters, the type of uncertainty in this study is assumed as random. Therefore, because the scenario-based robust optimization is one of the methods applied to tackle the randomness uncertainty (see Fig. 4), we utilize this approach in our study.

Fig. 4

Classification of uncertainty types for available data and the corresponding applicable modeling methods (According to Bairamzadeh et al. (2018))

To solve optimization problems with data uncertainty, a robust approach was proposed in the early 1970s and has been widely studied and developed (Bairamzadeh et al. 2018). Under this approach, the solution tends to accept an optimal answer for the nominal values of data to ensure that the optimal response is available when the data is changed (Mohammed et al. 2018; Özmen et al. 2017).

In the aforementioned robust optimization approach, two kinds of variables exist: (1) design variables and (2) control variables. Decisions related to design variables are made before the potential parameters are realized and cannot be adjusted after realization. Time control variables are subject to tuning and trigger a particular occurrence of potential parameters. Also, the model’s limits include structural and control constraints. Structural constraints refer to equations without uncertain parameters or variables, whereas control constraints include non-deterministic parameters or variables.

According to Mulvey et al. (1995), a typical mathematical formulation for a robust optimization model is represented in Eq. (16). The x vector reflects design variables, and the y vector describes control variables. A, B, and C are the parameter coefficient vectors and b and e are the parameter vectors (the right hand side values). A and b are certain values, while B, C, and e are uncertain. A special understanding of these parameters is known as a scenario that is determined by s index in these parameters. The probability of each scenario is determined by $p_s$. The $\Omega$ symbol is employed to represent a set of scenarios. Consequently, the coefficients specifying uncertainty are $C_s$ and $B_s$ for each scenario ($s \in \Omega$). Also, the control variable y is modified after awareness of the scenario and can be replaced with $y_s$ regarding scenario s. As a consequence of the uncertainty of the parameters, the model may not be justified for some scenarios. Therefore, $\eta _s$ is defined to represent the model under unjustified scenario s. Once the model is justified, $\eta _s$ is equal to zero, and in other situations, it will gain a positive number.

$$\begin{aligned}&Min \quad \sigma (x, y_1, y_2, \ldots , y_s) + \gamma \rho (\eta _1, \eta _2, \ldots , \eta _s)&\nonumber \\&s.t.&\nonumber \\&Ax = b,&\nonumber \\&B_sx + C_sy_s + \eta _s = e_s \quad ,&\nonumber \\&x \ge 0 \quad , \quad y_s \ge 0 \quad , \quad \eta _s \ge 0 \quad , \quad \forall s \in \Omega&\end{aligned}$$

(16)

The objective function represented in Eq. (16) includes two terms. The first term calculates the robustness of the solution which shows the risk-aversion level of decision-makers and their desire for lower costs. The second part calculates the robustness of the model by penalizing the solutions that violate the control constraints. The trade-off between the model robustness and the solution robustness is incorporated using coefficient (weight) $\gamma$ . To better explain the effect of $\gamma$, if we insert a small value for this parameter, the objective function focuses on minimizing the first term, and the probability of obtaining an infeasible solution increases. Whereas, if $\gamma$ is large, the solution tends to be more feasible, but the first part of the objective function (i.e. $\sigma (x, y_1, y_2, \ldots , y_s)$) takes higher values. The $\xi$ symbol and the array of $\xi = f(x,y)$ are specified as cost and utility functions, respectively. For each scenario, the high variance for $\xi _s=f(x,y_s)$ determines that the decision is taken at high risk. In other words, a tiny variation in the uncertain parameters can result in large variations in the value of f function. Mulvey et al. (1995) employ the terms formulated in Eq. (17) to illustrate the solution’s stability. $\delta$ is a weight reflecting the solution variance.

$$\begin{aligned} \sigma (0) = \sum _{s\in \Omega } p_s\xi _s + \delta \sum _{s\in \Omega } p_s \bigg ( \xi _s - \sum _{s\in \Omega } p'_s \xi '_s \bigg )^2 \end{aligned}$$

(17)

Since the square term of Eq. (17) (i.e. $\sum _{s\in \Omega } p_s ( \xi _s - \sum _{s\in \Omega } p_s' \xi _s')^2$) increases the computational time of solving the model, Yu and Li (2000) introduce the absolute value of the term, shown in Eq. (18), to reduce the operations related to the total computational time.

$$\begin{aligned} \sigma (0) = \sum _{s\in \Omega } p_s\xi _s + \delta \sum _{s\in \Omega } p_s \bigg | \xi _s - \sum _{s\in \Omega } p'_s \xi '_s \bigg | \end{aligned}$$

(18)

Dealing with Eq. (18), which contains an absolute value and outlines a non-linear function, two additional variables $\mathcal {Q}_s ^+$ and $\mathcal {Q}_s ^-$ are defined to linearize the resultant objective function. If $\sum \nolimits _{s \in \Omega } p'_s \xi '_s$ is more than $\xi _s$, $Q_s^-$ is returned and otherwise $Q_s^+$. Therefore, Eq. (18) is reformulated as follows:

$$\begin{aligned}&\sigma (0) = \sum _{s\in \Omega } p_s\xi _s + \delta \sum _{s\in \Omega } p_s (\mathcal {Q}_s ^+ + \mathcal {Q}_s ^-)&\nonumber \\&s.t.&\nonumber \\&\xi _s - \sum _{s\in \Omega } p'_s \xi '_s = \mathcal {Q}_s ^+ + \mathcal {Q}_s ^-, s \in \Omega ,&\nonumber \\&\mathcal {Q}_s ^+, \mathcal {Q}_s ^- \ge 0, \quad s \in \Omega .&\end{aligned}$$

(19)

According to the constraints of Eq. (19), it is clear that one of the values of $\mathcal {Q}_s ^+$ and $\mathcal {Q}_s ^-$ is always zero for any $\delta$ $\ge$ 0 (Lee 2011). Using Eq. (16), the objective function of the final robust optimization model is formulated as follows:

$$\begin{aligned} \sum _{s\in \Omega } p_s\xi _s + \delta \sum _{s\in \Omega } p_s (\mathcal {Q}_s ^+ + \mathcal {Q}_s ^-) + \gamma \sum _{s\in \Omega } p_s \eta _s \end{aligned}$$

(20)

Utilizing the abovementioned robust optimization method, the objective functions of our proposed problem are formulated as follows:

$$\begin{aligned}&MinZF = \sum _s p_s OBJ1_s + \lambda \sum _s p_s \bigg ( OBJ1_s - \sum \limits _{'s} p'_s OBJ1'_s + 2\theta _s \bigg ) + \omega \sum _s p_s \delta _s&\end{aligned}$$

(21)

$$\begin{aligned}&MinRF = \sum _s p_s OBJ2_s + \lambda \sum _s p_s \bigg ( \bigg ( OBJ2_s - \sum \limits _{'s} p'_s OBJ2'_s \bigg ) + 2\theta _s \bigg )&\end{aligned}$$

(22)

Several new constraints should be added to the model, as introduced in Eqs. (23)–(25), where $\lambda$ is the coefficient related to the importance (weight) of optimality robustness and $\omega$ reflects the infeasibility weight that a decision-maker sets experimentally. The first and the second terms in Eqs. (21) and (22) indicate the mean and variance of each objective function, respectively.

$$\begin{aligned}&OBJ1_s - \sum _s p_s OBJ1_s + \theta _s \ge 0 xm{\qquad } \forall s&\end{aligned}$$

(23)

$$\begin{aligned}&OBJ2_s - \sum _s p_s OBJ2_s + \theta _s \ge 0 xm{\qquad } \forall s&\end{aligned}$$

(24)

$$\begin{aligned}&\theta _s \ge 0&\end{aligned}$$

(25)

The last term in Eq. (21) measures the model robustness in terms of the infeasibility values of control constraints under each scenario. Constraints (23) to (25) are auxiliary constraints included in the optimization model for converting the nonlinear objective function to a linear one.

5 Solution approach

As previously mentioned, the model presented in this paper defines two minimization objective functions with different orientations. Therefore, when seeking interactivity between the objective functions, we employ an IMCGP to solve the problem. The model presented in this section is a combination of two different methods explained in the following subsections. We also compare the results of our solution approach with other methods using a real case study and several related numerical examples to create expected levels for our goals.

5.1 Improved multi-choice goal programming (IMCGP)

One of the most effective ways to increase the efficiency of an optimization model is to incorporate the experts’ opinions into the problem. To this end, the goal programming method describes the level of achievement for each of the objective functions according to the experts’ opinions. It is identified as an efficient, well-defined way to solve multi-objective models (Yadollahinia et al. 2018). We employ this method to solve our proposed multi-objective model.

Recently, a new multi-choice goal programming (MCGP) approach was proposed by Jadidi et al. (2015). The superiority of this model in comparison with the other MCGP models is the recommended methodology in which the decision-makers can control their priorities more efficiently. The authors present a model that contains the revised goal programming approach (introduced by Chang (2008)) and the original goal programming along with a priority function, taking into account goal efficiency. They believe that sometimes the value of the target function will pass our expectation level, resulting in a penalty for the optimization model. The following equations introduce their model:

$$\begin{aligned}&{{Max}} \sum _{k} (w_k^a a_k - w_k^b \beta _k)&\nonumber \\&s.t.&\nonumber \\&f_k (X) = \alpha _k f_{k,min} + (1 - \alpha _k) f_{k,max} + \beta _k(f_k^- - f_{k,max}) \qquad \forall k&\nonumber \\&\alpha _k \le y_k \le 1 + \alpha _k \qquad \forall k&\nonumber \\&\beta _k + y_k \le 1 \qquad \forall k&\nonumber \\&y_k \in \{0, 1\} , \quad 0 \le \alpha _k , \quad \beta _k \le 1 \qquad \forall k&\end{aligned}$$

(26)

In Equation set (26), the proposed single-objective optimization model for the MCGP is developed in which k is the number of objective functions that should be converted to maximization functions. The range of $[f_{k,min},f_{k,max}]$ determines a boundary for the aspiration level $y_k$ specified by the decision-makers ($f_{k,min} \le y_k \le f_{k,max}$). $\alpha _k$ is a continuous coefficient, valued between 0 and 1, and calculates the normalized distance between the k-th objective function and $f_{k,max}$ ($\alpha _k=\frac{f_{k,max} - f_k(X)}{f_{k,max} - f_{k,min}}$). $f_k^+$ and $f_k^-$ indicate the k-th value of the objective function in the desired and undesired conditions, respectively. $\beta _k$ also defines the normalized distance between the k-th value of the objective function ($f_k(X)$) and $f_{k,max}$ in case $f_{k,max}$ is greater than $f_k(X)$ ($\beta _k=\frac{f_k(X) - f_{k,max}}{f_k^- - f_{k,max}}$). $w_k^a$ and $w_k^b$ are the weights specifying the importance of the k-th objective with respect to $\alpha _k$ and $\beta _k$.

Jadidi et al. (2015) assume that $f_{k,min}=f_{k}^+$ and divide the range of $[f_k^-,f_k^+]$ into two suboptimal regions of $[f_{k,max},f_{k,min}]$ and a less favorable boundary of $[f_k^-,f_{k,max}]$. They note that one of $\alpha _k$ and $\beta _k$ is zero in each of these boundaries. Figure 5 illustrates the boundaries introduced by the authors. LDR and MDR stand for the less and more desirable ranges, respectively.

Fig. 5

Relationship between parameters in the proposed IMCGP approach (according to Jadidi et al. (2015))

The single-objective model introduced in Equation set (26) can be rewritten for our bi-objective model as follows:

$$\begin{aligned}&{{Max}} Z = w_1^a \alpha _1 + w_2^a \alpha _2 - w_1^b \beta _1 - w_2^a \beta _2&\nonumber \\&{\text {S.t:}}&\nonumber \\&Z_1 = \alpha _1 f_{1,min} + (1 - \alpha _1) * f_{1,max} + \beta _1 * (f_1^- - f_{1,max})&\nonumber \\&Z_2 = \alpha _2 f_{2,min} + (1 - \alpha _2) * f_{2,max} + \beta _2 * (f_2^- - f_{2,max})&\nonumber \\&\alpha _1 \le y_1 \le 1 + \alpha _1&\nonumber \\&\beta _1 + y_1 \le 1&\nonumber \\&\alpha _2 \le y_2 \le 1 + \alpha _2&\nonumber \\&\beta _2 + y_2 \le 1&\nonumber \\&y_1, y_2 \in \{0,1\}&\nonumber \\&\alpha _1, \alpha _2, \beta _1, \beta _2 \ge 0&\end{aligned}$$

(27)

The values of $f_k^+$, $f_k^-$, $f_{k,min}$ and $f_{k,max}$ can be obtained using the abovementioned method for our minimization functions:

• To obtain the value of $f_k^+$ we solve a sub-problem with the k-th objective function and all of the constraints to minimize the objective, and the achieved solution is equal to $f_k^+$.

• To estimate the value of $f_k^-$, a sub-problem is solved to maximize the k-th objective function and the solution is equal to $f_k^-$.

• The value of $f_{k,min}$ is obtained using a manner similar to $f_k^+$.

• To obtain the value of $f_{k,max}$, a sub-problem with the corresponding objective is solved to maximize the function. $f_{k,max}$ is less than or equal to the achieved solution (based on the decision-makers’ opinion).

The pseudo code of the proposed algorithm is presented in ”Appendix B”.

5.2 Heuristic approach

Since the computational time for solving an MILNP model increases drastically by adding the linearization binary variables, in this section, we consider a heuristic solution approach for our proposed problem given the circumstances of uncertain data. We introduce our new heuristic method in three steps as shown in Fig. 6. These steps are applied to the MINLP model as a heuristic MINLP (HMINLP) model for medium and large sample sizes. Table 3 introduces each optimization model and the corresponding solution methodology defined in this research.

Fig. 6

Steps defined for the proposed heuristic solution approach

Table 3 Definition of the proposed optimization models and the corresponding solution approaches

6 Case study

A study on a real-world operational case makes it possible to understand the applicability of our model. We selected a carbon black manufacturer in Iran where the environmental issues are of utmost importance to the government and decision-makers. In this section, initially, some explanations about the firm are presented to specify how the random parameters have been estimated for the relevant processes. We also utilized the opinion of the firm’s experts for a better estimation of the necessary parameters in our proposed model.

Carbon black is an essential additive for producing rubber. Although the product is a useful raw material for many industries, it has negative implications for both human health and our climate. Therefore, the design of a holistic SC concerned with environmental issues is crucial for decision-makers. Iran Carbon Company¹ produces carbon black (industrial carbon black) used by rubber factories. At present, the capacity of carbon black production in this company is over 36 thousand tons of industrial soot. The company’s raw materials include furfural extract, cracked fuel oil (CFO), and fluid catalytic cracking (FCC), which are mainly purchased from Abadan Refinery, Amirkabir, Bandaremam, Shazand, Tabriz, and Jam petrochemical companies. Although the company produces only carbon black, it is able to meet customers’ requirements via several products (e.g. N220, N330, N339, N375, N550, N660) with its high-tech packing system.

In this study, we consider three scenarios, namely pessimistic, most likely and optimistic ones. The highest occurrence probability is associated with the most likely scenario. Moreover, the values of the proposed model’s parameters are estimated according to the opinion of the company’s experts. As noted in Sect. 5.1, this study applies an improved MCGP method to solve the proposed model. Hence, the parameters related to this approach (e.g. weights of the objective functions, $f_{k,min}$, and $f_{k,max}$) are estimated based on the experts’ opinions as well. Other parameters relative to the proposed solution approach are collected from similar papers, such as Jadidi et al. (2015). Tables 4 and 5 show the values of certain and uncertain parameters used in our model, respectively. The monetary values are reported with MIRR (million Iranian Rials, the currency of Iran). In addition, the data is collected according to the opinions of the experts working in the carbon black manufacturer.

Following the study of Mohammed et al. (2017), three types of vehicles, i.e. light truck, mid-size truck, and heavy-duty truck, are contemplated. The values of carbon emission factors and transportation costs for each of these types are given in Table 6. The $\overline{\delta }_{vts}$ parameter was estimated by the carbon emissions caused by each vehicle type in kg per ton of carrying load of carbon black in every km distance. $\overline{CT}_{jvts}$ parameter was estimated by the average cost of transportation from suppliers using each type of vehicle in MIRR per ton of carbon black carrying load in every km distance.

Table 4 Case study: estimation of the certain parameters introduced in the model

Table 5 Case study: estimation of the uncertain parameters introduced in the model under the occurrence of different scenarios

Table 6 Case study: estimation of transportation-related parameters

To evaluate the proposed model, several numerical examples have been generated and employed in the sensitivity analysis tests. The model was coded in GAMS software using a computer system with a dual-core 1.40 GHz Pentium CPU and 3 GB of RAM. Numerical examples are presented in four different problem sizes introduced in Table 7, each of which has been examined and tested at five different levels of uncertainty (penalty costs $P=\{0.1-1.0\}$). We solve our proposed MINLP and MILP models, separately, with certain data (using the deterministic solution) and five uncertainty levels of data (using the robust solution), then compare them with our combined robust-heuristic solution, introduced in Sect. 5.2.

Table 7 Case study: problem sizes defined for the numerical tests

We also investigated the value of the objective functions (Obj1 and Obj2) in both deterministic and robust cases according to the various penalty costs defined for the availability of data. As it can be seen in Table 10, every objective function value in the deterministic model is greater than the corresponding value of the robust approach for each of the five penalty costs of uncertainty. The values also increase once we have more available data (as the penalty cost is greater). These trends can be found in any of the MINLP, MILP, and HMINLP models in each of the four problem sizes. Moreover, in each problem size and penalty cost, the target value of the MINLP model is lower than the corresponding one for the MILP and HMINLP models. The values of the objectives increase accordingly for the HMINLP model. Although we observe this slight increase in the values for the HMINLP model (which is not desirable for our minimization problem), the computational times of solving the problems, shown in Table 11, affirm the merit of the proposed heuristic approach, especially for solving the HMINLP model for the bigger problem sizes. Figures 7 and 8 illustrate the comparison of the objective functions (reported thoroughly in Tables 10 and 11) in terms of various penalty costs. According to these reasonable trends of the values of objective functions in both deterministic and robust approaches, we can conclude that the models are stable and well-integrated.

6.1 Consideration of different carbon policies

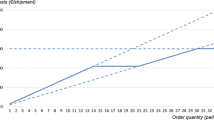
We now examine the first objective function of our model, introduced in Eq. (1), to explore the total cost of the SC with respect to several conditions of data availability or uncertainty. Aimed at comparing the carbon-tax policy, in which the carbon price is constant, with the cap-and-trade policy, we explore the effect of changing carbon capacity in each of these policies, separately. Figure 9 illustrates the result of the proposed HMINLP model under the condition of certainty and a constant carbon price ($cp=10$). Figures 10 and 11 show the results of the total cost under uncertainty conditions and this constant price. We focus on investigating the effect of changes in carbon capacity on total costs and carbon emissions in the chain.

Figure 9 shows that by increasing carbon capacity, the total cost is reduced and carbon emissions increase, but by a specific level of carbon capacity (the point near 45.5 tons). Until this point, the carbon emission curve shows a linear increasing trend per carbon capacity, and consequently, a consistent decline in total cost; however, after this level, more carbon capacity will result in unvarying total cost and carbon emissions. This means that if the carbon capacity is set to this value as its maximum level (45.5 tons), both the minimum total cost will add the highest carbon emissions. Figure 9 also determines a trade-off level (e.g. the break-even point 43.8) for the contrary criteria of decision-making—namely total cost, total carbon emission, and carbon capacity. Upon investigation of the model’s formulas, carbon capture constraint (Eq. 7) is a fundamental limitation for the optimization model and hence directly manipulates the trends shown in Fig. 9. We also can perceive that by reducing carbon capacity from 47 to 42 tons, carbon emissions will decrease by 8%, resulting in an overall cost increase of 0.2%. This affirms that a slight increase in inventory and transportation costs would result in a greater decline in carbon emissions. This would be a beneficial strategy for companies that are under governmental and environmental pressure for their gas emissions pollution.

Fig. 7

Case study: comparing the optimal values of the first objective function for each model and penalty cost

Fig. 8

Case study: comparing the optimal values of the second objective function for each model and penalty cost

Fig. 9

Case study: impact of carbon capacity on total cost and carbon emissions under certainty condition and carbon-tax policy

It can be seen in Fig. 9 that the values of total cost are changing in a limited range (between 7.16 and 7.30). This may occur because the source of uncertainty of all parameters has been assumed as a uniform normal distribution (see Tables 4 to 6). It is possible considering different types of distributions for generating the value of the parameters that would lead to significantly different results.

Under conditions of uncertainty, Figs. 10 and 11 illustrate similar behaviors as per certain conditions, shown in Fig. 9. By exploring these two charts, we see that while the levels of uncertainty increase (decreasing the penalty cost P), the amount of the total cost increase is negligible for the decision-makers. For instance, in the lowest carbon capacity of 42 tons, by increasing the level of uncertainty by 400% (from $P=0.8$ to $P=0.2$) the total cost is only boosted by 5% (from 4.55 to 4.77 MIRR), which concludes that the robust strategy outperforms at higher uncertainty levels than at its definitive state. The same justification can be represented for the negligible decrease in carbon emissions, shown in Fig. 11.

Fig. 10

Case study: effect of carbon capacity on total cost at different levels of uncertainty under carbon-tax policy

Fig. 11

Case study: effect of carbon capacity on carbon emissions at different levels of uncertainty under carbon-tax policy

Figures 12 and 13 demonstrate the relationship between the carbon capacity and total cost in both the definite and non-deterministic (in penalty cost 0.5) conditions, respectively. Each line in Fig. 12 determines the total cost of the chain per different carbon price and carbon capacity. For a fixed carbon price per ton, cp, increasing carbon capacity allows the company to pay less carbon tax, and hence the overall cost decreases. Similar to Fig. 10, these trends indicate that carbon capacity has a reverse relationship with the total cost. As far as the effect of carbon prices on total cost is concerned, we see a specific point for carbon capacity (43 tons). With carbon capacities below this point, any increase in the carbon price leads to an increase in the total cost of the chain; with carbon capacities above this point, the trend is in contrast. This is a noteworthy point that decision-makers can compare with the governmental “cap” on emissions, and if the determined cap is greater ($>43$ ton), the company is a potential carbon trader. Consequently, the total cost will decrease more with the help of higher carbon prices. However, once the governmental cap is below this point ($<43$ ton), the company will pay taxes. Increasing the carbon price leads to paying more taxes and, consequently, total cost. In this situation, it is recommended to buy permits to extend the cap to more than 43 tons.

Comparing Figs. 12 with 13 demonstrates the fact that under uncertainty conditions, shown in Fig. 13, the trends are similar to the certainty condition, but the specific point for comparing the governmental cap is lower (29 tons compared to 43 tons). This is also intuitive because decision-makers consider lower carbon capacities in their plans under the cap-and-trade policy and uncertainty conditions.

Fig. 12

Case study: effect of carbon capacity on total cost at different carbon prices under the cap-and-trade policy and certainty condition

Fig. 13

Case study: effect of carbon capacity on total cost at different carbon prices under the cap-and-trade policy and uncertainty conditions

If we compare the total cost calculated in the carbon-tax policy with the total cost of the cap-and-trade policy in certainty conditions (comparing Fig. 9 with Fig. 12) and in the uncertainty situations (comparing Figs. 10 with 13), we realize that the total cost is lower in the cap-and-trade policy. This suggests that the company should select the cap-and-trade policy if both policies are available. Moreover, in the case of carbon emissions, we calculated emissions in the cap-and-trade policy under uncertainty conditions ($P=0.5$) and demonstrated the results in Fig. 14. The figure illustrates that, although the company can take the advantage of the price increase for trading and consequently lower emissions in the cap-and-trade policy, it cannot decrease carbon emissions at the same increasing rate assumed for the carbon price. For instance, when the carbon price is doubled (from $cp=5$ to $cp=10$), carbon emissions decrease by only 1.7% (from 23.35 to 22.95).

Fig. 14

Case study: effect of different carbon prices on carbon emissions under the cap-and-trade policy

For a better understanding of the comparison of the two policies in the uncertainty conditions ($P=0.5$), we ran the HMINLP model by a fixed carbon capacity at 45 tons and the carbon price at 10 MIRR per ton for both the deterministic and robust-heuristic approaches, as shown in Table 8. A comparison of the total cost and total carbon emissions in Table 8 confirms that the cap-and-trade policy has the lowest total cost and carbon emissions as compared with the carbon-tax policy in both the definitive and complex robust-heuristic solutions approaches. Although the cap-and-trade policy presents more flexibility to buy and sell carbon in the carbon market than the other policy, decision-makers can decide if their priority is to minimize total costs or minimize overall carbon emissions. Table 8 illustrates that in case of both cost and carbon emission minimization, the cap-and-trade policy is the best option.

Table 8 Case study: total cost versus carbon emissions under different carbon policies using various models

6.2 Consideration of different vehicle types

For highlighting the contribution of this study regarding the consideration of assorted vehicle types, we compare the result of the proposed MINLP, MILP, and HMINLP models, considering all three types of vehicles (large, medium, and small trucks), with the models using only one of the types. As it can be seen in Fig. 15, in the “base case” model which employs all vehicle types, we achieved the minimum values for both total cost (the first objective function) and total carbon emissions (the second objective function). This result confirms the importance of considering various types of vehicles in any GSC and SSC, regardless of uncertainty in input data or the selection of another solution approach. Given that both total costs and total carbon emissions are the main factors of sustainability in the SC, the consideration of assorted vehicle types will ensure organizers to obtain higher sustainability performance using the proposed model.

Fig. 15

Case study: comparison of total cost and total carbon emissions considering types of vehicles

6.3 Sensitivity analysis on the objective functions

As mentioned in Sect. 5.1, the important parameters of our proposed IMCGP approach are the normalized distances between the k-th value of the objective function ($f_k(X)$) and the $f_{k,max}$. Table 9 demonstrates the effects of changes in the critical parameters of our proposed model, (i.e. demand, transportation cost, and carbon emissions factor) on the normalized distances defined for our two objective functions. The “base case” stands for the original values employed in the case study. As shown in the table, any increase in demand, transportation cost, and carbon emissions factor leads to an increase in the alpha parameter and a decrease in the beta parameter. Since the goal of the optimization model is to maximize alpha and minimize beta (according to the definitions of $\alpha _k$ and $\beta _k$ in Sect. 5.1), the result of the table illustrates the positive effect of demand and negative effect of transportation cost and carbon emissions factors on the goals of the problem. Moreover, by considering the total cost as the more important objective function optimized in the MDR range (see Fig. 5), we obtained $\beta _1 = 0$, and accordingly, for the less important objective function optimized in the LDR range, $\alpha _2 = 0$. The table also illustrates that the changes in the parameters influence the $\beta$ more than $\alpha$ (see the normalized distance ranges for each parameter), which means that the proposed IMCGP approach tries to arrange the second objective function in the LDR range in farther distances, aimed at finding optimal solutions.

Table 9 Case study: sensitivity analysis of the critical parameters of the model concerning the normalized distances of objective functions

6.4 Deviation variation from ideal objectives

Regarding our proposed IMCGP approach, we calculated the deviation of the objective functions from the lower limit of the ideal objective function ($f_k^-$ in Eq. (27)). Figure 16 illustrates the results of the deviations from the ideal values. As can be seen, once the problem size increases, the deviations, which are unpleasant in our IMCGP model, will increase. Since the deviations intuitively determine the situation of achieving ideal objectives, the result of the test on deviations specifies that in the case of larger problem sizes, the goal programming approach would take more distance from the ideal objectives defined in the model, particularly from the greenness goal (less total carbon emissions (Obj2)). Moreover, the scale of the values gained for the deviations demonstrates low variations from the ideal objectives; however, as the deviations increase with problem size, it is suggested that for much larger problem sizes, the company should check the deviations to determine the divergence from the greenness objective.

Fig. 16

Normalized deviation values from the lower limit of the ideal objective functions

6.5 Statistical evaluation of the proposed moles

In order to investigate the efficiency of the proposed approach, the ANOVA test has been conducted based on the results of Table 10. To compare and evaluate the obtained results, the least significant deviation (LSD) at the confidence level of 95% is considered as the statistical measure. Figure 17a, b show the LSD charts for the first and the second objective functions, respectively. It can be observed that there is not significant difference between the results of traditional (i.e MILP and MINLP) and heuristic approaches that confirms the efficiency of the proposed approaches to obtain optimal/near-optimal solutions.

Fig. 17

LSD diagram for the objective functions per different models (confidence level = 95% and the pooled standard deviation is used to calculate the intervals)

7 Managerial implications

This research provides a roadmap for decision-makers to compare carbon emission policies in SCs (carbon-tax and cap-and-trade) and select the most appropriate policy for their design. Although governments still encourage companies by presenting incentives on pricing carbon emissions through the carbon tax, according to our comparison of total costs and carbon emissions in two different policies, both costs and emissions were lower in the cap-and-trade policy. In general, and confirmed by our case study analysis, it seems that in any SC, governmental incentives for the cap-and-trade policy would be more effective for the organization in lowering pollution by investing in cleaner technologies and adopting greener practices (Theguardian 2013; Banik et al. 2020).

In practice, key environmental merit exists for the cap-and-trade over the other policy; it gives more confidence to managers about the level of emissions reductions they can achieve by implementing this policy. However, managers have little certainty about the price of emissions by selecting this policy (related to the emissions trading market). In contrast, the carbon-tax policy gives confidence about the monetary gain of the plan but little certainty about the level of emissions reductions. Today, environmental concerns are prominent in any country; therefore, from this point of view, we can also conclude that the cap-and-trade policy is more effective. As this policy is very simple, it can be implemented in just a few months. In theory, the adoption of the cap-and-trade system seems to be more complex for governments, as it requires the establishment of an emissions trading market. This means that if the trading market is implemented efficiently, the SCs will be more likely to implement the cap-and-trade than carbon-tax policy.

An application of assorted vehicle types in our GSC model demonstrated an appropriate effect on both costs and emissions. In general, governments and related organizations should provide the infrastructure required to employ different modes of transport or vehicle types. Our results confirmed that the usage of multi-mode transportation leads to a substantial decrease in the environmental damage caused by the SC. Reduction of costs per vehicle and products handling times for the SC results in a decrease in customs controls for governments and even low rates of theft or damage to the cargo for the insurer companies. Generally, it is suggested that governments define some incentives for SCs to apply multi-mode transportation in their networks.

The results of this study regarding the impact of the carbon emissions capacity parameter on both profitability and environmental impacts affirm that the bargaining power of both companies and governments is an important issue in determining the value of this parameter. Our case study was an example for one country; however, in countries with high levels of air pollution, the governments should consider lower values for the carbon emissions capacity because lower values of this parameter lead to a greater decrease in environmental damage caused by the SC. On the other hand, if countries require more production and supply for the products, increasing the value of the carbon cap parameter can be on the government’s agenda (NYT 2019).

Despite an examination of our approach by a case study with three scenarios, there are various ways for designing scenarios that can be addressed and compared with this paper. For instance, Fattahi et al. (2017) apply a scenario tree to generate scenarios for stochastic parameters. In their method, in the outset, they consider 200 scenarios and then the scenarios are converted into a scenario tree by reducing the number of scenarios. Given that managers usually develop a limited number of strategies/scenarios to navigate the kinds of extreme events they have recently seen in the real cases, it is suggested to keep the number of scenarios as least as possible. This will also decrease the level of complexity in the understanding of the model’s behaviour in different scenarios.

8 Conclusion

In this study, an environmentally-friendly GSC model was introduced to integrate the minimization of economic features with the minimization of environmental impacts of carbon emissions. A framework for planning sustainable logistics was presented in which various vehicle types and gas emissions in transportation, and other SC operations, were considered. Uncertainty was considered in demand and most of the costs related to the operations of the GSC, as well as for the carbon emissions factor caused by every vehicle. The proposed bi-objective multi-supplier, multi-product, multi-carrier, and multi-period model was solved by an improved algorithm for the multi-choice goal programming solution approach. A novel robust-heuristic optimization approach, HMINLP, was also developed to deal with demand and economic uncertainty, especially in larger problem sizes.

A real case study of an SC company was introduced to implement the model and test the efficiency of the proposed solution methodology. The results of the numerical tests in the case study demonstrated that the robust-heuristic approach could efficiently mitigate demand and economic uncertainty, and the heuristic solution could decrease computational times substantially for large-scale problems, despite the slight change in the objectives. To achieve environmental sustainability, we compared the carbon-tax policy with the cap-and-trade policy as they pertain to changing carbon capacity and concluded that, under the carbon-tax policy, an increase in the levels of uncertainty would lead to a negligible increase in total cost. This confirmed that the robust strategy outperformed at higher uncertainty levels than the definitive state. An examination of the cap-and-trade policy demonstrated a lower total cost compared to the other policy and affirmed that decision-makers should select the cap-and-trade policy if both policies are available. The tests on the consideration of various vehicle types confirmed the importance of this assumption in designing the GSC and SSC, regardless of uncertainty or the selection of another solution approach.

As for the limitations of our study, we assumed a fixed carbon capacity and price during the time horizon for avoiding further complexity in the model; however, the government can lower the carbon capacity each year to encourage companies through incentives to invest in clean technologies. In such situations, then, the model can be developed with consideration to various carbon capacities and prices for the defined periods. As we pointed out in the Introduction Section, improving service levels beyond reducing operating costs would be a competitive strategy for the GSC and SSC. In our study, we only focused on the costs associated with the SC, however, the trade-off between supply and demand—namely service levels of the SC—in all customer zones could be maximized in one of the objective functions beyond other cost minimization. Several other resilience factors, e.g. capacity disruption, can be included in the problem to configure a more resilient GSC (Ivanov 2018). Incorporating features of responsiveness for an SC, e.g. minimizing the lead-time or total transportation time, would be another direction for future research. In case of the solution approach, a suggestion for future research is the use of meta-heuristic methods and the development of new approaches to refine non-linear, mixed-binary models. Finally, an integration of sustainability with digital supply chains and Industry 4.0 systems can be considered a crucial future research avenue (Mrugalska and Stasiuk-Piekarska 2020; Dolgui et al. 2020; Ivanov et al. 2020).

Appendices

Appendix A: Detailed results of case study

Table 10 Case study: comparison of the MINLP, MILP and HMINLP models solved by the proposed deterministic, robust, and robust-heuristic solution approaches

Table 11 Case study: comparison of the CPU computational times (in seconds) for solving the MINLP, MILP, and HMINLP models by the proposed deterministic, robust, and robust-heuristic solution approaches

Appendix B: Pseudo code of the proposed approach